О решении некорректно поставленной задачи для нелинейного дифференциального уравнения методом проекционной регуляризации

В статье рассматривается задача с обратным временем для полулинейного дифференциально-операторного уравнения.

Данная задача поставлена некорректно, поэтому основными вопросами при ее исследовании являются вопросы построения устойчивого приближенного решения и оценки погрешности приближенного решения.

Для линейных некорректно поставленных задач вопросы построения приближенных решений и оценки погрешности построенных приближенных решений на классах корректности рассматривались, например, в работах В.К. Иванова, В.Н. Страхова, их учеников и последователей (см., напр., [1-3]) . Были введены понятия оптимального и оптимального по порядку метода приближенного решения [1].

Соответствующие понятия были введены и для нелинейных некорректно поставленных задач [4, 5].

Пусть H - гильбертово пространство, M с U , а C [ H] - пространство непрерывных отображений, действующих в H .

Рассмотрим операторное уравнение

A o u = f ; u е H ; f е H ,                                  (1)

где А 0 е C [ H ] - взаимно-однозначный оператор.

Предположим, что при f = f ₀ существует точное решение и ₀ уравнения (1), которое принадлежит множеству M , но точное значение правой части нам не известно, а вместо него дано приближенное значение f ₆ е H такое, что Н f ₀ - f g Н < 8 . Требуется по исходным данным задачи M и f g определить приближенное решение уравнения (1) и оценить его уклонение от точного решения.

Определение 1. Семейство операторов {T g :0 <  8 < 8 0 } будем называть методом приближенного решения уравнения (1) на множестве M , если для любого 8е (0 ; 8 ₀] оператор T g непрерывно отображает пространство H в H и T 8 f 8 ^ и ₀ при 8 ^ 0 равномерно на множестве M при условии Н A 0 и ₀ - f 8 Н < 8 .

Рассмотрим следующую величину, характеризующую точность метода {T : 0 <  8 <  8 ₀ } на множестве M :

Д ( T 8 ) = sup{ | | и - T 8 f 8 1| : и е M , || А ^ и - / 8 Н < 8 }.

Обозначим

®1( т ; M ) = sup{ || и 1 , и 2 Н : и_ь и 2 е M , Н A « 1 - A и 2 Н < т }

Математика

модуль непрерывности оператора, обратного к A 0 , на множестве A o M .

Определение 2. Метод {Т ₆ :0 <  5 <  5 ₀} будем называть оптимальным по порядку на множестве M , если существует число к такое, что для любого 5 е (0 ; 5 ₀ ]

А ( Т ₅ ) <  кю_х( 3; M ) .

Различные подходы к приближенному решению нелинейных некорректно поставленных задач предложены и исследованы, например, в монографиях [6-9] и статьях [10, 11].

В настоящей работе предложен метод приближенного решения полулинейной обратной задачи (модификация метода проекционной регуляризации) и доказана его оптимальность по порядку на одном из классов корректности.

1.    Задача с обратным временем для дифференциально-операторного уравнения.

Пусть H - гильбертово пространство, A - линейный неограниченный положительно определенный самосопряженный оператор с областью определения D ( A ), плотной в H .

Рассмотрим задачу вычисления элемента фе H , такого, что решение задачи Коши du du = -Au + f (t,u(t)); tе (t0;T),                                    (2)

dt

u ( t ₀) = ф , фе H , 0 <  t ₀ <  T , удовлетворяет условию u(T ) = X - Здесь f : [ t ₀ ; T ] x H ^ H - отображение, удовлетворяющее условию Липшица по переменной и и условию Гельдера по переменной t , т.е. существуют постоянные L >  0 , K >  0 и 0 <  а <  1, такие,

H f (U1, t) - f (и 2, t )|H < L H U1 - и 2lH для всех t1,12 е [10; T], u1, и2 е H .

Зафиксируем число r >  0. Рассмотрим множество

M = { ф е D ( e^{At 0} ): H e^{At 0} ф ||< r }.

Предположим, что при заданном хе H существует точное решение фе H поставленной обратной задачи, принадлежащее множеству M .

Элемент хе H нам не известен, а вместо него дано приближенное значение X 5 е H , такое, что H X — X s Н < 5 . Требуется по исходным данным задачи определить приближенное решение ф₆ задачи с обратным временем и оценить его уклонение от точного решения.

Задача Коши (2) равносильна интегральному уравнению u (t) = e - A(t - t 0ф + j e - A(t-T) f (t, u (t )) dT                               (3)

t 0

(см.. напр., [12]).

Рассмотрим величины:

щ ( M , 5 ) = sup{ || ф 1 - ф 2 H : ф 1 , ф 2 е M , H X 1 — X 2 H < 5 } - модуль непрерывности для нелинейной обратной задачи,

( M , 5 ) = sup{ H ф 1 - ф 2 H : ф 1 , ф 2 е M , H X ^>1 - ; ^ 2 H < 5 } -

Наряду с нелинейной обратной задачей, рассмотрим соответствующую обратную задачу для линейного уравнения, т.е. задачу вычисления элемента фе H такого, что решение задачи Коши dv = -Av; t е (10;T), dt

v(10) = ф, фе H, 0 < 10 < T, удовлетворяет условию v(T) = ;X, где X е H - заданный элемент.

Рассмотрим величины:

щ ( M , 5 ) = sup{ H ф 1 - ф 2 H : ф 1 , ф 2 е M , H X 1 - X 2 H < 5 } модуль непрерывности для нелинейной обратной задачи,

( M , 5 ) = sup{ H ф 1 - ф 2 H : ф 1 , ф 2 е M , H ; X 1 - ; ^ 2 H < 5 }

-

-

модуль непрерывности для соответствующей линейной обратной задачи.

Справедлива следующая лемма (см. [13 ).

Лемма. Существует 5 ₀ >  0, такое, что для всех 5 <  5 ₀ выполняются неравенства

<у ( M , e - ^LT 5 ) <  < M , 5 ) < < у ( M , e LTe LT 5 ) .

3. Метод приближенного решения задачи с обратным временем.

Обозначим через { E ^ : X >  0} разложение единицы, порожденное оператором A. Пусть A _a -линейный ограниченный оператор в H , определяемый формулой

α

A α u

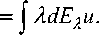
о

Вместо неустойчивой обратной задачи для уравнения (2) рассмотрим задачу вычисления элемента фa = ua(t0), где ua(t) удовлетворяет условиям du^ = -AaUa(t) + Eaf (t,ua(t)), te (10,T);

dt                                                                         (4)

u ^a ( T ) = E a X .

Рассмотрим задачу Коши du^ = -AaUa(t) + Eaf (t,ua(t)), te (10,T);

dt                                                                         (5)

u ^{a (} t 0 ) = Ф a ^, где Ф а = ^E a Ф a ^.

Так как Aa - ограниченный самосопряженный оператор в H, то задача Коши (5) равносильна интегральному уравнению ua(t) = e-Aa(t-t0)E^a + J e-Aa(t-T)Eaf (t,ua(t))dT.                        (6)

t 0

Выполняется

Теорема. Для любого элемента X ^е H существует элемент ф = ф_а е E _a H , такой, что решение u ( t ) задачи Коши (5)удовлетворяет условию u ^a ( T ) = E _aX .

Доказательство. Рассмотрим решение задачи Коши (5), которое удовлетворяет также интегральному уравнению (6) Из (6) следует, что функция u ^a ( t ) удовлетворяет также уравнению

T ua(t) = eAa(T-t)EaX- J eAa(t-T)Eaf (t,ua(t))dT                         (7)

t

Рассмотрим в пространстве C ([ 1 ₀ ; T ] ^ H ) непрерывных функций на [0 ; T ] со значениями в H норму

|| и |^ = max e-kt И u(t) |H, эквивалентную норме

| и |C = max И и (t) | H t0 < t < T пространства C([10;T] ^ H). Рассмотрим оператор Pa, действующий в C([10;T] ^ H) по прави лу

T

P a U = e A ^{a ( T} — t ) E a % - J e A ^{a (} t ^-T ) E a f ( T, и ( T )) d T.

t

Имеем неравенство (для любых u 1 , и ₂ е C ([0 ; T ] ^ H ))

Математика

T

П Р _а и₁ - Р _а и ₂ | k <  Le ^a max e ^{- k (} t ^-T ) e ^{- k T} 1 1 u₁( T ) - и ₂ ( t ) | | H — T <

1 0 <  t <  T^j_t

T                  1 _ e - kT

< Le ^{а T} | u₁ - и ₂ | k max e~ ^{k (} t ^-T ) d T <  Le ^{а T} --------H u₁ - и ₂ | k .

• t ₀ <  t <  t-                            k

• 4.    Оценка погрешности метода проекционной регуляризации.

Выбирая k >  Le^aT , убеждаемся, что отображение Р _а является сжимающим в пространстве C ([ t ₀ ; T ] ^ H ) с нормой H • || _k . Следовательно, уравнение (7) имеет единственное решение в C ([ t ₀ ; T ] ^ H ). Обозначим В _а : H ^ Е _а Н оператор, действующий по правилу

ВаХ = «“(tо) , где иа(t) - решение уравнения (7). Тогда ф“ = иа (t о) = ВаХ -                                   (8)

искомый элемент, определяемый элементом х однозначно. Теорема доказана.

Обозначим ф^а = и ^а (t ₀), где и ^а ( t ) - решение задачи (4); ф д = ф д ( t ₀), где и д ( t ) - решение задачи (4) с приближенными исходными данными. В качестве приближенного решения задачи с обратным временем рассмотрим элемент ф ^ ( ^д ) = Р _а ( д ) Х д при подходящем выборе зависимости а = а ( д ).

Рассмотрим величину

А м ( а , д ) = sup{ || ф^а - ф || : фе M , | х - Х д Н < д }, характеризующую точность построенного метода приближенного решения задачи (2) на введенном множестве M .

Воспользуемся неравенством

А м ( а , д ) < А 1 ( а ) + А 2 ( а , д ) , где

А 2 ( а , д ) = sup | ф д - ф^а | ;

• II Х ^- Х д 11< ^д

А 1 ( а ) = sup | ф^а - ф | .

ϕ ∈ M

Оценим величину А ₂( а , д ). Рассмотрим функцию v _а ( t ) = e ( t ^- t ^{0) а} и _а ( t ). Функция v _а ( t ), очевидно, удовлетворяет дифференциальному уравнению ^α

• —¹² =- ( А а - а Е ) v ^а ( t ) + Е а д а (t , v ^а ( t )) , t е ( 1 0 , T ) ,                      (9)

dt где да (t, v) = Eаe(t-t0)а f (t, e-t-tо)аv): [10; T] x H ^ H - отображение, удовлетворяющее условию Липшица по переменной v и условию Гельдера по переменной t , t е [t0; T].

По построению функция va (t) удовлетворяет также условиям va( t 0) = фа;

vа( T) = e(T - t 0)ах.(11)

Решение задачи Коши (9), (10) удовлетворяет интегральному уравнению

t va(t) = e-Аа-аЕ)(t-t0)Еа фа + J e-Аа-аЕ)(t-T)Еа да(Т, Vа(т))-T .(12)

t 0

Из равенства (12) при t = T с учетом (11) следует равенство

T eа(T-t0)ЕаХ = e4Аа-аЕ)(t-t0)Еа фа + J e4Аа-аЕ)(T-Т)Еа да(T, Vа(T))-T.(13)

t 0

Из (13)следует

T e-(Aa-aE)(t - t0) Ea^a = ea(T - t0) EaX - J e—(Aa-aE )(т-t) Ea ga (T, Va (t )) dT.(14)

t 0

Подставляя выражение (14) в равенство (12), имеем

T va (t) = e(Aa-aE)(T-t)ea(T-t0)Eax - J e(Aa-aE)(T-t)Ea ga (t, va (t))dT.(15)

t

Аналогично, функция V g ( t ) удовлетворяет уравнению

T

Va5 (t) = e(Aa-aE)(T—t)ea(T—t0)EX, - Je(Aa-^)T-t)EagaT, vg(T))dT .(16)

t

Из (15) и (16) следует неравенство

T

|| va - vg(t) H<| e(Aa-aE)(T-t) Hea(T-t0) Hx - Xs H+ L JHe(Aa-aE)(T-t) HH va - a (t) H dT.(17)

t

Из неравенства (17) с учетом леммы Гронуолла и неравенства

|| e ⁽ A a ^{-a E )( T -} t ) H < max e ⁽ A ^{-a )( T -} t ) <  1

0 следует

|| v ^a ( t ) - v g ( t ) H < e ^{a ( T -} t ⁰⁾ e^{L ( T -} t )S, откуда при t = 1 ₀

|| ф^a - ф g H < e ^{a ( T -} t ⁰⁾ e^{L ( T -} t ⁰⁾ S .

Следовательно, для величины A ₂ ( a , S ) имеем оценку

A ₂( a , S ) <  e ^{a ( T -} t ⁰⁾ e LTe L S                                   (18)

Оценим величину A 1 ( a ). Рассмотрим функцию u ( t ), удовлетворяющую интегральному уравнению (3) и функцию u _a ( t ), удовлетворяющую (6) и функцию u ( t ) = E _a u ( t ). Рассмотрим равенство

T u (t) = eAa(T-t)EaX - J eAa(T-t)Eaf (t, u (t))dT.                           (19)

t

Из (3) следует равенство

T

X = e ^- A ^{( T -} t ⁰⁾ ф + J e ^- A ^{( T -T} ) f ( t, u ( t )) d T.                              (20)

t 0

Подставляя выражение (20) в равенство (6) и учитывая, что eAa(T-t)Ea = eA(T-t)Ea, имеем равенство tT ua(t) = e-A(t-t0)Eaф + J e-A(t-T)Eaf (t,u(t))dT + Je-A(t-T)Ea(f (T,u(T)) - f (T,ua(T))dT. (21) t 0

С учетом равенства (19) из (21) следует

T ua (t) - u (t) = Eau (t) - u (t) + J e- A(t-T) Ea( f (t, u (t )) - f (t, ua(T)) dT(22)

t

Из (22) с учетом неравенства || e^{A ( T -} t ) E _a || <  e ^{a ( T -} t ) следует

T

• e-a(T-t) ||ua(t) - u(t)|| < e-a(T-t) ||Eau(t) - u(t)|| + LJe-a(T-T) |ua(T) - u(t)|dT.(23)

t

Из (23) в силу леммы Гронуолла

I u ^{a (} t ) ^- u ⁽ t )|| <  e L ⁽ T - t ⁰⁾ | E a ^{u (} t ) ^{- u (} t )||.

Математика

Следовательно,

А 1 ( а ) < e^{L (} T - t ⁰⁾ sup { \ Ф - Е _аф \ Ф^ M} = e^{L (} T ^- t ^о) д 1 ( а ) < e^{L (} T ^- t ^о) re^{-at 0} .

Выберем зависимость α=α∗(δ). из условия eα(T -t0)δ= eLT re-αt0                                         (24)

(см. [14]). Из (24) следует , что

α ^∗ ( δ ) = ¹ ln( re^{L ( T - t 0)} / δ ) .

Таким образом, оценка погрешности метода проекционной регуляризации на множестве M с выбором параметра регуляризации из условия (24) имеет вид

T - t ₀ t ₀

Δ _M ( α ^∗ ( δ ) , δ ) ≤ e^{L ( T - t 0)} r^T δ ^T .                                (25)

Так как модуль непрерывности для полулинейной обратной задачи на множестве M удовлетворяет неравенству

T - t ₀ t ₀

ω ( M , δ ) ≤ e^{L ( T - t 0)} r^T δ ^T

(см. [13]), то из оценки (25) следует теорема.

Теорема. Метод проекционной регуляризации приближенного решения задачи с обратным временем, определенный равенством (8), оптимален по порядку на множестве M .