О решении нелокальной обратной задачи для параболического уравнения
Бесплатный доступ
Исследуется задача с обратным временем для параболического уравнения с нелокальными краевыми условиями. Исследуемая задача возникает, например, при математическом моделировании процесса внешнего геттерирования пластин кремния при создании полупроводниковых приборов. Как правило, математические модели интенсивных диффузионных и тепловых процессов учитывают также эффекты, связанные с нелинейностью процесса. Предлагается подход к построению численного решения задачи с обратным временем. Приближенное решение, устойчивое по Адамару, строится с помощью метода регуляризации, основанного на добавлении к финальному условию переопределения слагаемого с малым параметром. Для получения оценки точности численного решения в постановке задачи используется дополнительная (априорная) информация, характеризующая точное решение. Получена оценка погрешности приближенного решения при заданной априорной информации.
Обратная задача, параболическое уравнение, метод регуляризации, математическая модель, оценка точности приближенного решения
Короткий адрес: https://sciup.org/147243216
IDR: 147243216 | DOI: 10.14529/mmph240206
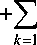
Список литературы О решении нелокальной обратной задачи для параболического уравнения
- Самарский, А.А. О некоторых проблемах теории дифференциальных уравнений / А.А. Самарский // Дифференц. уравнения.– 1980. – Т. 16, № 11. – С. 1925–1935.
- Муравей, Л.А. Об одной задаче с нелокальным граничным условием для параболического уравнения / Л.А. Муравей, А.В. Филиновский // Матем. сб. – 1991. – Т. 182, № 10. – С. 1479–1512.
- Муравей, Л.А. Об одной нелокальной краевой задаче для параболического уравнения / Л.А. Муравей, А.В. Филиновский // Мат. заметки. – 1993. – Т. 54, № 4. – С. 98–116.
- Ионкин, Н.И. Решение одной краевой задачи теории теплопроводности с неклассическим краевым условием / Н.И. Ионкин // Дифференц. уравнения. –1977.– Т. 13, № 2. – С. 294–304.
- Ионкин, Н.И. Об устойчивости одной задачи теории теплопроводности с неклассическим краевым условием / Н.И. Ионкин // Дифференц. уравнения. – 1979. – Т. 15, № 7. – С. 1279–1283.
- Егоров, И.Е. Неклассические операторно-дифференциальные уравнения / И.Е. Егоров, С.Г. Пятков, С.В. Попов. – Новосибирск: Наука, 2000. – 335 с.
- Пятков, С.Г. Разрешимость краевых задач для операторно-дифференциальных уравнений смешанного типа / С.Г. Пятков, Н.Л. Абашеева // Сиб. матем. журнал – 2000 – Т. 41, № 6. – С. 1419–1435.
- Кожанов, А.И. Нелокальные задачи с обобщенным условием Самарского–Ионкина для некоторых классов нестационарных дифференциальных уравнений. А.И. Кожанов / Докл. РАН. Матем., информ., проц. упр. – 2023 – Т. 509. – С. 50–53.
- Кожанов, А.И. Пространственно–нелокальные краевые задачи с обобщенным условием Самарского–Ионкина для квазипараболических уравнений / А.И. Кожанов, А.М. Абдрахманов // Сиб. электрон. матем. изв. – 2023 – Т. 20, № 1. – С. 110–123.
- Пулькина, Л.С. Нелокальная задача с интегральными условиями для квазилинейного гиперболического уравнения / Л.С. Пулькина // Матем. заметки – 2001 – Т. 70, № 1 – С. 88–95.
- Тагиев, Р.К. Вариационная постановка коэффициентной обратной задачи для многомерного параболического уравнения / Р.К. Тагиев, Ш.И. Магеррамли / Итоги науки и техники. Серия «Современная математика и ее приложения. Тематические обзоры». – 2022. – Т. 212 – С. 92–99.
- Тагиев, Р.К. Вариационная постановка одной обратной задачи для параболического уравнения с интегральными условиями / Р.К. Тагиев, Ш.И. Магеррамли / Вестник Южно-Уральского государственного университета. Серия «Математика. Механика. Физика». – 2020 – Т. 12, № 3 – С. 34–40.
- Иванчов, Н.И. Краевые задачи для параболического уравнения с интегральными условиями / Н.И. Иванчов / Дифференц. уравнения – 2024 – Т. 40, № 4 – С. 547–564.
- Камынин, В.Л. Об обратной задаче определения правой части в параболическом уравнении с условием интегрального переопределения / В.Л. Камынин // Матем. заметки. – 2005. – Т. 77, № 4. – С. 522–534.
- Данилкина, О.Ю. Об одной нелокальной задаче для уравнения теплопроводности с интегральным условием / О.Ю. Данилкина // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. – 2007. – Т. 1, № 14. – С. 5–9.
- Юлдашев, Т.К. Нелокальная краевая задача для линейного псевдопараболического уравнения высокого порядка / Т.К. Юлдашев, Н.А. Суюнова // Журнал математики и информатики. – 2023. – Т. 3, № 2. – С. 69–78.
- Иванов, В.К. Теория линейных некорректно поставленных задач и ее приложения / В.К. Иванов, В.В. Васин, В.П. Танана. – М.: Наука, 1978. – 206 c.
- 18 Васин, В.В. Некорректные задачи с априорной информацией / В.В. Васин, А.Л. Агеев. – Екатеринбург: Наука, 1993. – 261 с.
- Табаринцева, Е.В. Об оценке точности метода вспомогательных граничных условий при решении граничной обратной задачи для нелинейного уравнения / Е.В. Табаринцева // Сибирский журнал вычислительной математики. – 2018. – Т. 21, № 3. – С. 293–313.
- Табаринцева, Е.В. О решении некорректно поставленной задачи для нелинейного дифференциального уравнения / Е.В. Табаринцева // Труды Института математики и механики УрО РАН. – 2015. – Т. 21, № 1. – С. 231–337.
- Исмати, М. (Исматов, М.) О некоторых несамосопряженных смешанных задачах теории теплопроводности / М. Исмати // Дифференц. уравнения. – 2005. – Т. 41, № 3. – С. 382–395.
