О решении одной граничной обратной задачи для параболического уравнения
Бесплатный доступ
Рассматривается задача восстановления граничных условий третьего рода по дополнительной информации о решении параболического уравнения. Рассматривается метод приближенного решения поставленной задачи с выбором параметра регуляризации по схеме М.М. Лаврентьева [1] и с использованием одной из схем апостериорного выбора параметра регуляризации. Получена точная по порядку оценка погрешности построенного приближенного решения на одном из классов равномерной регуляризации.
Обратная задача, метод приближенного решения, оценка погрешности
Короткий адрес: https://sciup.org/147158643
IDR: 147158643
Текст научной статьи О решении одной граничной обратной задачи для параболического уравнения
— = —y-a(x)w (0 < х < 1; t > 0), и(х,0) = 0; м(0,?) + ^0^(0,?) = 0 dt дх и дополнительному условию
м(хо,О = p(t), хо Е (0,1), t > 0.
Здесь а(х) 6 С2[0,1], а(х) > 0, h0, hA - заданные постоянные, и(«,/)еС2(0,1)ПС([0,1]); k(x,*)g 1Т2 (0,оо).
Рассматривая вспомогательную «прямую» задачу
Эи d2u , .
— = —т - а(х)и, dt дх2
m(x,O) = O;m(O,Z) + Aomx(O,Z)=:O; ы(х0,/) = /?(/), где а(х)еС2[0,1], х g (0,х0), Z > 0, u(*,t) е С2(О,хо)ПС([О,хо]); Дх^е И^1 (0,°о), определим функцию q(t)-ux(x0,t). Следовательно, исходная задача сведется к задаче восстановления функций v(0 = m(U)h w(t) = ux(\,t), где u(x,t) удовлетворяет условиям: ди д2и — =—--а^и, u(x,O) = O;u(xQ,t') = p(ty,ux^xo,t) = q(t), (3)
dt дх хе (х0,1), t > 0.
Сведение задачи (3) к задаче вычисления значений неограниченного оператора
Пусть функции p(t),q(t),p\tyq\t) в задаче (3) принадлежат Л2(0,и). Рассмотрим вспомога тельную прямую задачу
ди dt
д2и , .
—v - а(х)и, дх2
w(x,0) = 0; и(хо,О = Р^У, uQ,t) = v(Z), хе (х0,1), t > 0.
Лемма 1. Пусть p(t),pXtyv(tyv’(t) е Z2[0,oo) . Тогда задача (4) имеет решение и(«,/)еС2(х0,1)ПС([х0,]]); u(_X,*)eW2 (0,оо).
Доказательство. Рассмотрим формальное решение задачи (4), которое может быть найдено методом Фурье: t 1
м(х, Z) = g(x, Z) + J ^G(x, У, t - r)/^, Tykdr, (5)
где gM^-F^x^-V^, №,) = 1Wz£W, + £WzWS2 1 - х0 1 - х0 1 - х0 1 - х0
G(x,^T) = ^e-^Xn^)Xn(x)
- функция Грина первой краевой задачи; Х„ (х) - собственные функции, образующие полную ортонормированную систему в ./^[xq,!], ~А~ собственные значения соответствующей задачи Штурма-Лиувилля. Рассмотрим следующие функциональные ряды, сходящиеся равномерно на [х0,1]:
У£М?.х-<Х?м?
П=1
(см. [6, с. 500]). Для произвольных Буняковского имеем оценки:
Коши- с учетом неравенства
П=1
И=1
П=1
|
<зирй.2е ^ Ai |
9 X Л=1 Лп J |
/2, |
ЧЛ=1 An J |
/2 |
c0 t ’ |
(6) |
|
|
^„№„'(Х) |
^supA^e Ai |
'^уСДх^ vn=l ЛП 7 |
1/2 |
|
1/2 |
A2’ |
(7) |
|
Х^ХДх) |
^supA^-A' 4 |
y«=i А? j |
1/2 |
'^ (Xn(^ 2-1 ^4 \n=l At > |
1/2 |
" i2 ’ |
(8) |
|
) Х„№п(х t |
) <^1-^ 4 |
'^ (X„(x))2 \ n=l лп |
Y/2 / |
<и=1 Лп |
\l/2 |
(9) |
Из неравенств (6)—(9) следует, что функция G(x,q,t) имеет непрерывные производные
Gx(x,g,t), Gxx(x,<;,t), Gt(x,$,f) при всех х,^е[0,1],/>10 >0 .
Рассмотрим произвольное число
t
> 0 и зафиксируем
t0, 0
СО 2
Л(х,?,г) = £^(<-А^(?)11^^(10)
л=1
и ряд, полученный почленным интегрированием (10):
ос / 2 00 1 _
^\Х^-тУг\Х^Хп(х^^----^---|X„(g)||Xn(x)|.(11)
И=1 /0 П=1 А1
Из оценки, аналогичной (6), следует сходимость ряда (11) при всех х,^ е [0,1]. По следствию из теоремы Б. Леви [7] ряд (10) сходится почти всюду на отрезке 0<т
Используя свойство абсолютной непрерывности интеграла, по заданному числу f > 0 выберем /0 > 0 такое, что
|С(х,£д-г)./(g, т^т
1й
Тогда
^x^^-t^J^xW
о
z0
^х^-тУ^тУт
о
^8<С
\/^,тУт
о
+ f хе[0,1] С учетом последнего неравенства из (5) следует оценка | и(х, t) 1< С max I g(x, t) I. хе[0,1] Рассмотрим ряд S(x,t,T) = ^Ht)e-^,-T)Xn(x), (И) n=l где /„(0 = \А5АХпАА§ = ^^рМ /^«W - коэффициенты Фурье функции f(x,t). Воспользуемся следующим утверждением [10, с. 414]. Утверждение 1. Существует такая постоянная С, что для каждого и и в каждой xg[x0,1] точке хп^- s"mAnx < —. и Из утверждения 1 следует, что *0 J^sinA„^ ^0 Так как существует такая константа с, что при каждом п 02 ЛИ (см. [10, с. 414]), то из оценок (12) и (13) следует существование такой постоянной D, что х0 ^Хп(^ х0 D при всех и. С учетом (14) и (15) из неравенства (11) следует |5(,,,,г)|<С|Иф1М21 <тахЯ3/2^Л,"г) f n=\ n=l Так как в силу утверждения 1 ряд в правой части (16) сходится при каждом хе[х0;1], то оценка (16) принимает вид №,t,f)|< г(х) Следовательно, функция S(x,t,r) суммируема на отрезке те [0,/] при каждом х. Далее, используя неравенство (5) |«^(х,/)|<С?!max|^(х,/1)[; |^^(х,/)|<С72max|g"(x,^)j; |г/,(д,/)|<С3 max |g(x,/)| + |g'(^0l хе[0,1 л-£[0,1 ухе[0,1] Из полученных оценок следует, что ^(^,1), ut(x,t) g С2(0,со) при любом х е [0,1]. Таким образом, функция и^хА является решением задачи (4). Из полученных оценок следует также, что к задаче (3) применимо преобразование Фурье на полупрямой / g (0,оо). Применяя к задаче (3) преобразование Фурье, имеем следующую задачу для линейного обыкновенного уравнения второго порядка: Uxx Здесь U(x,A) = Fu = ^e”i;uu(x,t)dt - образ Фурье функции u(x,t\ о Обозначим через ф(х,0 решение уравнения (17), удовлетворяющее условиям Теорема 1. Существуют постоянные С,, С2, С3, С4, Dx, D2, D3, D4, т такие, что С,—””7=—~ -I Пт^) I- С2 S ; с3 ch 4а(х - х0) <| фх(х, А) |<С4 ch4~А{х- х0); nA nA Dx ch 4~A(x - x0) <| i//(x, A) |< D2 ch д/Я(x -x0); D34a sh 4~A(x - x0) <| фх(x,Я) |< D44a sh V^(x - x0) при A > r. Доказательство теоремы аналогично проведенному в [2]. Решение задачи (17) имеет вид U(A) = P(AMV) + ^W), ww = Р(Л>ХМ + QWX(1,A). Рассмотрим следующие линейные нормированные пространства: Z,2(0,co) - пространство функций, суммируемых с квадратом, определенных при /е[0,да) (принимающих действительные значения), X = L2(0,co)x Т2(0,да); ф - пространство функций, допускающих аналитическое продолжение в полуплоскость Imz < О и таких, что 11 F^s + icr) |2 ds <С при всех ст < 0; У = Ф х Ф . Выполняется следующая теорема (см., напр., [9]) Теорема 2. Класс функций Ф совпадает с классом функций, представимых в виде FW = О ОО где интеграл сходится в среднем и J| /(?) |2dt < да. о Рассмотрим равенство Парсеваля J| ДО |2^ = 2я J] ДЯ)|НЯ 0 -ОО (см. [8]). Так как, очевидно, для функции /(Z) с действительными значениями выполняется равенство F^-A^ = У'(Я), то из равенства Парсеваля следует /|/(?)|2Л = 4л- j\F(A)pdA. о о Следовательно, линейный оператор Fo : ZL2 [0,1] -» Ф, действующий по правилу fqW- 2.4л \e-utf^dt, о является изометрией. Значит, пространства X и У также изометричны. Таким образом, задача (3) сводится к задаче вычисления элемента еК VW4 такого, что W))=r HU) ^(1,Я) YPW) a(pW ^(А)) (yHU) фх(1,А)Хе(А)) <д(А),’ где А :У -> У - неограниченный линейный оператор. Метод приближенного решения Пусть вместо точных исходных данных p(t),q(t) в задаче (3) известны 3- приближения ^(^^(О и уровень погрешности 3>0 такие, что Ц/^-^Ц^^; ||^-^||<. Пусть известно также, что при точно заданных начальных данных p(t), q^ задача (3) имеет решение, принадлежащее классу равномерной регуляризации Mr = {(v,w) е X; (v^w^gX, ||(v',w')||% 5 г}. Используя метрическую эквивалентность задач (3) и (6), построим предварительно приближенное решение задачи (6). Известно, что при заданных начальных условиях Р и Q задача (6) имеет решение, принадлежащее классу равномерной регуляризации Мг={СеГ; AGgY, ||2G||y<г}. Требуется построить устойчивое приближенное решение задачи (3) и оценить его уклонение от точного решения. Рассмотрим регуляризованные начальные данные: vU0 = v5(0*(9E(t) = ^v6(t-TX(T)dT; wj(t) = w6(t)*юЕ(?) = Jm^(t-т)®Е(r^dr. где e ^(0 = 112 + А ’ В качестве приближенного решения задачи (3) будем рассматривать элемент <>W) Аб А образ Фурье которого имеет вид -А6-Ле Таким образом, в качестве приближенного решения задачи (6) рассматривается элемент ZE5W = Ae-X6P8=A£P5. (19) Оценка погрешности метода проекционной регуляризации Рассмотрим приближенное решение (18) задачи (17). В качестве характеристики точности приближенного решения (18) рассмотрим величину A(s, А) = sup {||gJ - g||: Z g Mr; \\Z - Zs || < a}. Воспользуемся очевидной оценкой АО^АД^ + А^), где A1(s) = sup{||Gf-G||: GgMA GE = AeZ , A2(f,5) = sup{|G^-G^^IZ-Z^U^^}. Оценим величины АД^), A2 (£,). Для величины A2(f,^) имеем очевидную оценку A2(f, <5") < Ц^^Ц, где ||Ла|| = maxfVz A е sp(BE), X > 0}, где BJ УДЫ) Ф^АЙ^А^ Ф^АА^х WU) ^(Ы)Д^(М) W)/ Далее, где е ММ)А "I о ^(Ы) кгЛ о J о о , В2 = 2 (ММ) ^(М) е"вХ Зафиксируем ^ > О. Рассмотрим матрицу с,А)= ИЛ)|2 ^OAWA) е-геХ Максимальное собственное значение матрицы Q имеет вид у = (Ы2 (М)+М2 (1АМа Следовательно, || Д || < sup Vkl2 ОА+М2IWEX - Из последнего неравенства и теоремы 1 следует существование постоянной Д такой, что ИаИа^25- Аналогично, максимальное собственное значение матрицы с2А) = IMWI2 ^ОАЖОА) ^алжсАР1^(М)12 , -2ея имеет вид Следовательно, ;М1^1А12+1М1А12К2£*. И < sup Vl^OAlAi^ ^а Из последнего неравенства и теоремы 1 следует существование постоянной Д такой, что И<А^. Из неравенств (19) и (20) следует существование постоянной Д > 0 такой, что A2(f,^) < рде15 . Оценка для величины А] (г) имеет вид A, (f) < sup {||(АЁ - Л)/ГА|: G е Mr} < г sup-—-— < rs. Л>0 Замечание. Оценивая снизу величины A](s) и A2(s,A), можно убедиться, что оценки (20) и (21) являются точными по порядку. Выбирая зависимость г = s(A) из условия 5егЕ — rs (квазиоптимальный выбор параметра регуляризации [4]), получаем, что оценка погрешности при ближенного решения (18) на множестве Мг имеет вид 6.W№<~^-. (22) Из замечания следует, что оценка (22) является точной по порядку. В силу изометричности преобразования Фурье из оценки (21) с учетом оценки погрешности приближенного решения задачи (17) следует теорема 2. При сформулированных выше условиях существуют постоянные 0;Сб;С7 такие, что для любого 8 g (0,80) справедливы оценки погрешности метода проекционной регуляризации на множестве Мг: 8) <........ ln(l/^) Ь(1/) Апостериорный выбор параметра регуляризации Для выбора параметра регуляризации на практике может быть использована следующая схема, не использующая явно априорную информацию о точном решении поставленной обратной задачи (ср. [7]). Пусть параметр регуляризации выбирается из конечного множества Лд, = {^:0 Обозначим через G® = REZS соответствующие приближенные решения. Пусть G - точное решение задачи (17), GeMr. Обозначим через е t квазиоптимальное значение параметра регуляризации, полученное по схеме М.М. Лаврентьева. Обозначим через е * оптимальное значение параметра регуляризации, выбираемое из множества XN, т.е. е* = шах{^ : 8, 6 М^Х^, где M(XN) = (8j е Ад,: rSj < 8е2Е' > Пусть M(XN)*0; Ад, \M(Ay) Ф 0 . Наряду с М(АУ) рассмотрим множество ' 1 ' A7+^) = LzGAw:||G^-GfJ|<4^ (у =0,1,...,/)> . Лемма 2. M(XN)^ M4XN) . Доказательство. Рассмотрим значения параметра регуляризации s,, 8j g XN; s, g Л/(Адг), j ||g/ -G® <||g^ -gI+Ig-G/ |+||Gf-G®, . <^5e1Ej . Следовательно, stg M+(Xn) . Обоснование одного из правил апостериорного выбора параметра регуляризации дает следующая теорема. Теорема 3. Пусть параметр регуляризации выбран из условия s* = max |s,: s, с Л/+(Лд,)^. Тогда А(е+(8), 8) = sup (||gJ - G||: G g M • l|Z - Zs II < . ) ln(l/^) Доказательство. Из определения s* = st следует, что для f/+1 выполняется неравенство Г£М > S_ Г£°Р‘ 1 ~ 1 ‘ g2ff/+1 e'2'Eopl Следовательно, в силу монотонности функции s(x) = ^- на промежутке яб(0,оо), f/+1 >80pt и е2х i i Зе^6м < 5е2Е°р' . В силу леммы 2, так как M(KN) с М+ (Л^) , £* = £,= max {Sj: е, е M(XN^<е* = max I s, : s4 e M* (Ад, Из определения M+ (Л^) следует A(£+(<5),5) = sup! Gj Gj -г* гз :ZGMr;\\Z-Z5\\<3 +sup Gj <48e2£* + 5e2s* + rs* <6^sfinX3\8A<— opt In(lM) Теорема доказана.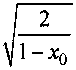
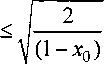
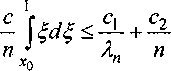
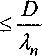
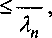
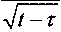
N>.
Список литературы О решении одной граничной обратной задачи для параболического уравнения
- Лаврентьев, М.М. О некоторых некорректных задачах математической физики/М.М. Лаврентьев. -Новосибирск: Наука, 1962. -92 с.
- Танана, В.П. Об оптимальном по порядку методе решения одной обратной задачи для параболического уравнения/В.П. Танана//Докл. РАН. -2006. -Т. 407, № 3. -С. 316-318.
- Ильин, A.M. Уравнения математической физики/A.M. Ильин. -Челябинск: Изд-во ЧелГУ, 2005. -171 с.
- Иванов, В.К. Дифференциально-операторные уравнения и некорректные задачи/В.К. Иванов, И.В. Мельникова, А.И. Филинков. -М.: Наука, 1995. -175 с.
- Танана, В.П. Об одном подходе к приближению разрывного решения некорректно поставленной задачи/В.П. Танана, Е.В. Табаринцева//Сибирский журнал индустриальной математики. -2005.-Т. 8, № 1(21).-С. 129-142.
- Владимиров, B.C. Уравнения математической физики/B.C. Владимиров. -М.: Наука, 1971.-512 с.
- Pereverzev, S. On the adaptive selection of the parameter in regularization of ill-posed problems/S. Pereverzev, E. Schock//SIAM J.Numer.Anal. -2005. -V. 43, № 5. -P. 2060-2076.
- Колмогоров, А.Н. Элементы теории функций и функционального анализа/А.Н. Колмогоров, С.В. Фомин. -М.: Наука, 1989. -496 с.
- Виленкин, Н.Я. Специальные функции и теория представлений групп/Н.Я. Виленкин. М.: Наука, 1965. -588 с.
- Дьедоне, Ж. Основы современного анализа/Ж. Дьедонне. -М.: Мир, 1964. -430 с.


