О решении одной обратной задачи, моделирующей двумерное движение вязкой жидкости
Автор: Андреев Виктор Константинович
Рубрика: Математическое моделирование
Статья в выпуске: 4 т.9, 2016 года.
Бесплатный доступ
Рассматривается обратная начально-краевая задача для линейного параболического уравнения, которая возникает при математическом моделировании двумерных ползущих движений вязкой жидкости в плоском канале. Неизвестная функция времени входит в правую часть уравнения аддитивно и находится из дополнительного условия интегрального переопределения. Поставленная задача имеет два разных интегральных тождества, которые позволяют получить априорные оценки решения в равномерной метрике и доказать теорему единственности. При некоторых ограничениях на входные данные решение построено в виде ряда по специальному базису. Для этого задача путем дифференцирования по пространственной переменной сводится к прямой неклассической задаче с двумя интегральными условиями вместо обычных краевых. Новая задача решается методом разделения переменных, позволяющим найти неизвестные функции в виде быстро сходящихся рядов. Другой, стандартный, метод решения исходной задачи состоит в сведении ее к нагруженному уравнению и первой начально-краевой задаче для него. В свою очередь, эта задача сведена к одномерному по времени операторному уравнению Вольтерры со специальным ядром. Доказано, что оно имеет решение в виде ряда. Установлены некоторые вспомогательные формулы, полезные при численном решении этого уравнения методом преобразования Лапласа. Установлены достаточные условия, при которых решение с ростом времени выходит на стационарный режим по экспоненциальному закону.
Обратная задача, априорные оценки, преобразование лапласа, экспоненциальная устойчивость
Короткий адрес: https://sciup.org/147159399
IDR: 147159399 | УДК: 517.956.27 | DOI: 10.14529/mmp160401
Текст научной статьи О решении одной обратной задачи, моделирующей двумерное движение вязкой жидкости
Рассмотрим начально-краевую задачу ut = vuxx + f (t) + g (x,t), u(x, 0) = uo(x),
x £ ( — 1 , 1) , t £ [0 , T ];
x £ ( — 1 , 1);
(0.1)
(0.2)
u ( - 1 ,t )= u 1( t ) , u (1 ,t )= u 2( t ) ,
j u ( x,t ) dx = q ( t ) , t £ [0 , T ] . (0.3)
- 1
Здесь функции g ( x,t ), u 0( x ), u 1( t ), u 2( t ), q ( t ) и постоянные v > 0, T > 0 считаются заданными, a u ( x,t ) , f ( t ) - искомыми. Таким образом, задача (0.1) - (0.3) является обратной. Для ее гладких решений необходимо потребовать выполнения условий согласования
u o( — 1) = u 1(0) , u 0(1) = u 2(0) , I u o( x ) dx = q (0) .
- 1
К задаче (0.1) - (0.3) приводит математическое моделирование двумерных ползущих движений вязкой жидкости специального вида, в плоском канале [1,2] или вязкой теплопроводной жидкости в модели микроконвекции [3]. При этом функция f (t) есть продольный вдоль канала градиент давления, который ищется вместе с полем скоростей и температур. Функции u 1(t), u2(t) задают движение стенок канала, a g(x,t) -известное распределение температуры в нем для уравнений микроконвекции. Третье условие (0.3) представляет собой заданный расход жидкости через поперечное сечение слоя. Постоянная v в уравнении (0.1) есть кинематическая вязкость жидкости. Конечно, возможна и чисто тепловая интерпретация задачи (0.1) - (0.3).
Следует отметить, что обратные задачи для параболических уравнений с интегральным условием переопределения более общего вида, чем (0.3), рассматривались в достаточно большом количестве работ, см., например, [4-8] и другие. Более полный обзор работ имеется в [9]. Как правило, в них доказывается существование и единственность решения, рассматриваются и обосновываются методы построения приближенных решений для случая (а он, по-видимому, представляет наибольшую трудность), когда неизвестная функция f ( t ) входит в правую часть основного уравнения (системы) мультипликативным образом.
В данной работе неизвестная f ( t ) входит в правую часть аддитивным слагаемым -это следует из постановок гидродинамических задач, упомянутых выше. Пользуясь спецификой задачи (0.1) - (0.3), ее одномерностью, удается получить достаточные условия сходимости ее решения к стационарному в равномерной метрике (в интегральной метрике подобный результат был получен в [7]), построить решение в виде рядов по специальному базису и тем самым решить уравнение второго рода для f ( t ), если перейти к задаче для нагруженного уравнения. Кроме того, получена конечная формула преобразования Лапласа ядра интегрального уравнения, полезная при численном нахождении f ( t ). Остальные гидродинамические характеристики: вертикальная компонента скорости, давление - легко восстанавливаются по функциям u ( x, t ), f ( t ) [2].
Произведем замену u ( x,t) = v ( x,t) + | [ u 1( t) + u 2( t)-q (t)] x2 + 2 Iu 2( t)-u 1( t)] x + 4 [3 q (t)-u i( t)-u 2( t)], тогда функции v(x,t), f (t) суть решение задачи
(0.4)
V t = vv xx + f ( t ) + h ( x,t ) , x G ( - 1 , 1) , t G [0 ,T ]; (0.5)
v ( x, 0) = u o( x ) - 4 I u 1(0) + u 2(0) - q (0)] x 2 - 2 [ u 2(0) - u 1 (0)] x
- 4 [3 q (0) - u 1 (0) - u 2(0)] = v o( x ); (0.6)
v ( ± 1 , t )=0 , vx ( x,t ) dx = 0 , t G [0 ,T ] , (0.7)
- 1
h ( x, t ) = g ( x, t ) - 4 [ u 1( t ) + u 2 (t ) - q ( t )] x 2 - 2 [ u 2( t ) - u 1( t )] x
- 4 [3 q ‘ ( t ) - u 1( t ) - u 2( t )] + 2 v [ u 1( t ) + u 2( t ) - q ( t )] (°-8)
и штрих означает дифференцирование по t.
Интегрирование уравнения (0.5) по x от — 1 до 1 с использованием второго условия (0.7) дает связь f (t) = 2 |[Vx (—1 ,t) — Vx (1 ,t)] — I h(x,t) X'
(0.9)
- 1
Итак, если u 1( t ) ,u 2( t ) ,q ( t ) npiina,тлежат C 1 [0 ,T ]. g ( x,t ) G C (( — 1 , 1) x [0 , T ]). to задача (0.1) - (0.3) эквивалентна задаче (0.5) - (0.7), причем f ( t ) определяется (по известной v ( x, t )) равенством (0.9). Ниже и изучается задача определения функций v ( x, t ) и f ( t ). Дополнительные требования на входные данные будут сформулированы позднее.
1. Априорные оценки
Лемма 1. Решение задачи (0.5) - (0.8) определяется единственным образом.
Доказательство. Умножение уравнения (0.5) на v ( x,t ) и интегрирование с использованием граничных условий (0.7) приводит к равенству
- Г1 [ at 2 J
- 1
v 2( x, t ) dx^ + v j v 2 ( x,t ) dx
- 1
j h ( x,t ) v ( x,t ) dx.
- 1
Поскольку в нашем случае имеет место неравенство Стеклова.
v 2( x, t )
, , 4
dx 6 — v X ( x,t ) dx,
π 2
- 1
то из (1.1) легко найти оценку
j v 2( x,t ) dx 6
- 1
[(У v 2( x ) dx ) + I
e n 2 VT/ 2 k ( т ) dT
2 e - π 2 νt
с функцией
k ( t ) = ( У h 2( x, t ) dx ) .
- 1
(1.1)
(1.2)
(1-3)
Из неравенства (1.2) и вытекает единственность определения v ( x,t ), а из (0.9) и f ( t ). □
Замечание 1. Если интеграл
∞ j в2VT/2k(т) dT (1.4)
сходится (это означает, что k ( t ) ~ в П 2 vt/ 2 при t ^ то ), то L 2-норма функции v ( x,t ) экспоненциально убывает с ростом времени t.
Оказывается, что можно получить оценку |v(x,t)|, равномерную по x G [—1, 1] и t G [0, T]. Для этого заметим, что наряду с (1.1) имеет место другое интегральное тождество
j v 2 dx +
- 1
v dt j v 2 dx
- 1
hv t dx,
- 1
откуда, учитывая обозначение (1.3),
v x 2 dx 6
- 1
I v 0 x dx +
- 1
t
J к 2( т ) dT.
(1.5)
В силу неравенств (1.2), (1.5) имеем
x v2 (x, t) = 2 J vvx dx 6 2
- 1
(У v 2 dx ) 1 ’ 2 (У v X dx ) ’ 2 6 2 [( ^ v 2( x ) dx )
- 1
- 1
1 / 2
+
t
+ I e n 2 VT/ 4 к ( т ) dT
x
(у v 0 x dx +
- 1
t
J к 2( т ) dT^ 0
1 / 2
e - π 2 νt/ 4
= k2 ( t ) e - 2 vt/ 4
(1.6)
поэтому
|v ( x,t ) | 6 k( t ) e - 2 vt/ 8 (1.7)
для всех x E [ — 1 , 1] и t E [0 ,T ]. Следовательно, если сходится интеграл (1.4), то функция к ( t ) ограничен а, для всех t E [0 , то ] i1 |v ( x,t ) | ^ 0 щ hi t ^ то равномерно по x E [ — 1 , 1].
Дифференцирование задачи (0.6) - (0.8) no t приводит к аналогичной задаче для vt(x,t), где нужно f (t) заменить на ft(t), h(x,t) нa ht(x, t), начальные данные (0.6) на vt(x, 0) = vv0xx + 2 -1 Здесь использовано уравнение (0.5) и равенство (0.9). Поэтому для vt(x,t) будут справедливы оценки (1.2), (1.7), где вместо к(t) будет функция k1 (t )=( jhx x,t) df, -1 (L9) а вместо v0(x) - функция v10(x) из (1.8). Значит, |vt(x,t)I 6 к 1(t)e-2vt/8 (1.Ю) с ограниченной функцией к i( t) =2 -1 v20(x) dx )1/ 2+j t en2VT/4кi(т) dT dx + -1 t 1/2 1/2 j к 2( т) ^t) J . (1.11) Оценку неизвестной функции f (t) получим следующим образом. Умножим уравнение (0.6) на полином 2-го порядка x2 — 1 и проинтегрируем по промежутку [—1, 1], найдем с использованием условий (0.7) представление для f (t), именно f (t)=3 j (x2— 1) h(x, t) dx -1 j(x2— 1)vt(x, t) dx -1 (1.12) Применение неравенств Коши - Буняковского к первому интегралу в (1.12) и (1.10) для второго интеграла дает оценку I f (t) I 6 \/| k(t) + ki(t)e-2vt/8 (113) с функциями k(t), k1(t) из (1.3) и (1.11) соответственно. В выражении для k1(t) функция k 1(t) определяется равенством (1.9). Замечание 2. Если дополнительно к (1.4) сходится интеграл ∞ I еп2VT/4ki(т) dT, (1.14) то k 1( t) ограничен а для всех t > 0 и |f (t) | ^ 0 пр и t ^ то по экспоненциальному закону. Кроме того, из (0.5) и оценок (1.7), (1.10) и (1.13) аналогичный результат имеет место и для |vxx|. Нами доказана. Теорема 1. Пусть v0(x) G C[—1,1] QC2(—1,1), h(x,t), ht(x,t) G C((—1,1) x [0,T]), ft(t) G C(0, T), и решение задачи (0.5) - (0.7) существует, тогда оно является единственным, и выполнены оценки (1.8), (1.10), равномерные для всех x G [—1, 1] и t G [0,T]. Если интегралы (1.4). (1.14) сходятся, то функции v(x, t). f (t) стремятся, к нулю с ростом времени по экспоненциальному закону. В следующем пункте устанавливается существование решения.
2. Построение решения в виде рядов по специальному базису Подстановка (0.9) в (0.5) приводит к нагруженному уравнению на v(x,t) и первой начально-краевой задаче для него. Однако мы пока этого делать не будем, а. поступим следующим образом. Поскольку в (0.9) входят неизвестные производные vx(± 1,t), продифференцируем уравнение (0.5) по хи введем новую неизвестную функцию w (x, t) = vx (x, t). (2.1) Она - решение начально-краевой задачи Wt = vwxx + hx(x, t), x G (—1, 1), t G [0,T]; (2.2) w(x, 0) = vоx(x) = wo(x), x G (—1, 1); w(x, t) dx = 0, -1 xw(x, t) dx = 0, -1 t G [0 ,T]. Первое из условий (2.4) следует из (2.1), так как x v (x,t )= I w(x, t) dx, (2.3) (2.4) (2.5) -1 а. второе - из интегрирования по частям второго равенства (0.7). Неклассическая начально-краевая задача (2.2) - (2.4) решается методом разделе ния переменных, именно ∞ w(x,t) — ^2 wk(t) sin цkx, k=1 Wk (t) — ak e^ kt + ak — 1 + цk Jw°( x)sin цxdx, -1 t У bk(T) e-νµ2k(t-τ)dτ, bk (t) — 1-#k µk jhx(x't)sin"kxdx- -1 (2.6) (2.7) (2.8) цk - положительные корпи уравнения tg ц — ц. причем [10] цk — € — €-1— 2€-3/3 + O (€ - 5), € — п (к + 1 / 2). Легко доказывается (см., например, [11, с. 381], [12]) что ряд (2.6) представляет собой классическое решение задачи (2.2) - (2.4) при t > е > 0 и wо(x) G C[— 1, 1]. hxЕ C([—1, 1] х[0,T]). Замечание 3. Система функций sinцkx является ортогональной в L2 на отрезке [-1,1] с нормой цk(1 + цk)-1 // и образует там базис. Эти функции есть решения задачи на собственные значения Xxx + XX — 0, x Е (—1, 1); ^X(x) dx — j xX(x) dx — 0 -1 -1 e X — Xk — цk. Из (0.9) и (2.6), (2.7) находим ∞ f (t) — —v^ Wk (t) sin Цk — k=1 jh(x,t) dx, -1 (2.9) а из (2.5) восстанавливаем v(x,t): re 1 v (x,t)— wk (t )(cos цk— cos цkx). (2.10) k=1 µk Искомая функция u(x,t) определяется из замены (0.4). Формулы (2.9), (2.10) и дают классическое решение задачи (2.2) - (2.4) при указанных выше условиях на w0(x), h (x, t). Замечание 4. Легко видеть, что f (t) в задаче (0.5) - (0.7) определяется только по четной части решения v(x, t). Действительно, пусть h(x,t) — h:(x,t) + h:(x,t). v0(x) — v40(x) + vn0(x) ii v(x,t) — v4 (x,t)+ vH (x,t). Тогда для vH (x, t) получим классическую первую начальнокраевую задачу для параболического уравнения с правой частью hH (x, t) и начальным значением vHо(x). Для четной части будет задача (0.5) - (0.7) с правой частью f (t) + h4(x,t), начальным значением v4о(x), а интеграл в (0.7) берется по промежутку [0,1]. Формулы (0.9), (2.9) упрощаются, f (t) — —vv,x.(1, t) — j h,:(x,t) dx — ∞ —v^Wk (t) sin Цk k=1 — 1 j h.(x,t) 0 dx. (2.11) Далее предполагается, что в задаче (0.5) - (0.7) v = v4, h = h4, vо = v4o, индекс “ч” всюду ниже опускается. Будем искать теперь решение первой краевой задачи для нагруженного уравнения (0.5), где f (t) определена первой формулой (2.11), в виде ряда Фурье ∞ v (x,t ) = ^ Vn (t ) cos (nx, (n = 2(2 n + 1), (2.12) при этом v(± 1, t) = 0, второе условие (0.7) использовано при выводе равенства (0.9). Представляя h(x,t) и v0(x) в виде аналогичных рядов с коэффициентами hn (t ) = 2 j h (x,t) cos (nxdx, vn0 = 2 j v0( x) cos (nxdx о о и пользуясь ортонормальностью базиса cos (nx, из уравнения (0.5) находим эффициентов ряда, (2.12) ДЛЯ KO- Vn (t) = Vn о e A f (T) + hn (T )1 e v^n(t T) dT. ξn (2.13) Из (2.11) получим ∞ f (t) = V 2(- 1)n(nvn (t) n=0 ∞ f (0) = v £( -1) ”(„v„ (0) n=0 - - j h(x t) dx, jh (X,0) dx. (2.14) Подстановка, vn (t) из (2.13) в (2.14) приводит к интегральному уравнению второго рода (уравнение Вольтерры) на f (t): t∞ f (t) = -2 v / f (T) 2 e 0 n=0 v^n(t-T) dT + m(t), (2.15) где m(t) = - / h(x,t) dx + v ^(-1)n(n pn0e 0 n=0 t v^nt + I hn(T)e-v5n(t-T) dT^, (2.16) m(0) = f (0). Ядро интегрального уравнения есть сумма ряда Дирихле K(у) = -2v ^2 e-v^ny, У = t - t. (2.17) n=0 Лемма 2. Функция f (t), определяемая вторым равенством (2.11), является решением интегрального уравнения (2.15). Доказательство. Проведем его для w0(x) = A sinцкx, где A = const, k - фиксированное, h(x,t) = 0. В общем случае доказательство проводится аналогичными выкладками. Из (2.11) f (t) = -vAe-v^ kt sin цк. а из (2.10) -v (x,t) = p-1Ae-v^ kt (cos pk - cos pkx). Значит, коэффициенты ряда Фурье начальной функции v0(x) = jk 1(cos jk — cos jkx) по системе cos ^nx имеют вид vn 0 2 A (—1) n sin jk <. (j k — en) ’ 6.=4+2у (2.18) Функция m(t) из (2.16) с помощью формулы (2.18) перепишется так: ∞ m (t) = 2vA sin jk n=0 e j k- νξn2t - С 2- n (2.19) Вычислим первое слагаемое правой части уравнения (2.15): t ∞ e v"kт E e-v5n(t-T) dT = о n=0 ∞ —e-^2kt E — n=0 <n - J I - ∞ e-νξn2t ^2—ё n=0 ^k ^n_| Сумма первого ряда в квадратных скобках равна [13, с. 688] 1 п _ \ _ 2 nj^k tg 2 ^kj , ^k = П ^k • Поскольку tg jk = jk, эта сумма есть 1 /2. Значит, правая часть (2.20) с учетом (2.19) и есть f (t) — m(t), что и доказывает лемму. □ Уравнение (2.15) можно решить и методом преобразования Лапласа, продолжив функцию h(x,t) нулем вне отрезка [0, T], считая, что при t = T она имеет разрыв 1-го рода [14]. Пусть ∞ u( p )=к"11 (t)dt есть преобразование Лапласа u(t). Тогда в изображениях уравнение (2.15) имеет ре- шение [15,16] откуда K( p) m(p) f(p) = m(p) + ----,— , 1 — K(p) t f(t) = m(t) +I k (t — t ) m (t) dr, 0 (2.21) где k(t) есть opигинал K(p)(1 — K(p)) 1. В нашем случае [14] из (2.17) ZS K (p) 1 — K( p) Поскольку [13] - ∞ 2 "Е n=0 p + v^n. ∞ 1+2 vE , « n=0 p+ v^ 2 v e \ Д th\ Д, n=0 p + v /X = k(p) • получим /X k (p) = th p/v лУp/v + th д/p/v (2.22) Формула (2.22) может быть полезна при численном решении уравнения (2.15). Замечание 5. Используя равенства (2.16), (2.22), можно доказать совпадение вы ражений для f (t) (2.11) ii (2.21).
3. О поведении решения при t ^ го Сначала найдем стационарное решение. В этом случае в задаче (0.6) - (0.8) начальные данные (0.7) не ставятся; функция hs не зависит от времени t, и решение vs (x), fs определяется по формулам x vs (x) = C 1 x + C2 — — x2 — j(x — z)hs(z) dz, -1 f s = 3 j z2h-(z) dz C1 j h(z) dz, 0 (3.1) C2 = ν + 2 z2^ hs(z) dz. Исходное решение us(x) найдется из замены (0.4) . . 3 _ , 1 _ 1 . . u (x) = v (x) + 4 (u 1 + u2— q )x2 + 2 (u2— u 1)x + 4 (3q — u 1 — u2). (3.2) В формулах (3.1) функция hs(z) считается четной согласно замечанию 2. Если в задаче (0.6) - (0.8) функция h(x, t) задана для всех t > 0, то возникает вопрос об асимптотическом поведении функций v(x, t) и f (t) при t ^ то. В частности, при каких условиях на h(x, t) решение задачи (0.6) - (0.8) с ростом времени выходит на стационарный режим (3.1)? Для ответа на этот вопрос произведем замену V(x, t) = vs(x) — v(x, t), F(t) = fs — f (t), (3.3) тогда, V(x,t) 11 F(t) являются решением задали (0.6) - (0.8) с заменой h(x, t) на, H (x,t) = hs (x) — h (x,t) и начальных данных (0.7) на V0 (x) = vs (x) — v0( x). Имеет место Теорема 2. При условии сходимости интегралов ∞∞ 0KW'2vv“- 0K"":"dT- (3.4) (3.5) (3.6) где K (t ) = (У H2(x,t) dx) , K1(t)= (УHt(x,t) dx) , -1 -1 решение задачи (0.6) - (0.8) с ростом времени t стремится к стационарному режиму (3.1) по экспоненциальному закону. Доказательство. Действительно, в этом случае для V(x, t) из (3.3) справедливы оценки (1.7), (1.10), а для F (t) - оценка (1.13) с указа иными выше заменами h (x,t) на, H(x,t) из (3.4) ii v0(x) iiа, V0(x) in (3.5). □ Замечание 6. В условиях теоремы 3 имеет место экспоненциальная устойчивость стационарного решения (3.1). В терминах исходных данных задачи (0.1) - (0.3) для ограниченности интегралов (3.6) достаточно потребовать сходимости интегралов ∞1 [g(x,T) 0 -1 - g"(x)]2dx en2VT/4dT, ∞1 У У gT(x,T) dxe"2vt/4dT; 0 -1 ∞ У [Uj (T) - uj|2en2"<4dT, j = 1, 2, 0 ∞ У [u(n)(T)]2en2VT/4dT, n = 0, 1,2, ∞ [[q(T) - q"]2e2VT/4dT, ∞ j[q(n)(T )|2 Z2VT/4 dT, n .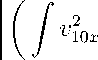
Список литературы О решении одной обратной задачи, моделирующей двумерное движение вязкой жидкости
- Andreev, V.K. Unsteady 2D Motions a Viscous Fluid Described by Partially Invariant Solutions to the Navier -Stokes Equations/V.K. Andreev//Journal of Siberian Federal University. Mathematics and Physics. -2015. -V. 8, 2. -P. 140-147.
- Andreev, V.K. On an Inverse Problem for Two-Dimensional Navier -Stokes Equation/V.K. Andreev//Abstracts of the International Conference Differential Equations and Mathematical Modeling. -Ulan-Ude, 2015. -P. 44-45.
- Mathematical Models of Convection/V.K. Andreev, Yu.A. Gaponenko, O.N. Goncharova et al. -Berlin: Walter de Gruyter GmbH & Co. KG, 2012. -417 p DOI: 10.1515/9783110258592
- Prilepko, A.I. Methods for Solving Inverse Problems in Mathematical Physics/A.I. Prilepko, D.G. Orlovsky, I.A. Vasin. -N.-Y.: Marcel Dekker, 1999.
- Cannot, J.R. Determination of a Parameter p(t) in Some Quasi-Linear Parabolic Differential Equations/J.R. Cannot, Y. Lin//Inverse Problems. -1988. -V. 4. -P. 35-45.
- Васин, И.А. О некоторых обратных задачах динамики вязкой несжимаемой жидкости в случае интегрального переопределения/И.А. Васин//Журнал вычислительной математики и математической физики. -1992. -Т. 32, вып. 7. -С. 1071-1079.
- Васин, И.А. Об асимптотическом поведении решений обратных задач для параболических уравнений/И.А. Васин, В.Л. Камынин//Сибирский математический журнал. -1997. -Т. 38, № 4. -С. 750-766.
- Кожанов, А.И. Параболические уравнения с неизвестным коэффициентом, зависящим от времени/А.И. Кожанов//Журнал вычислительной математики и математической физики. -2005. -Т. 45, № 12. -С. 2168-2184.
- Пятков, С.Г. О некоторых классах линейных обратных задач для параболических систем уравнений/С.Г. Пятков, Е.И. Сафонов//Сибирские электронные математические известия. -2014. -Т. 11. -С. 777-799.
- Олвер, Ф. Введение в асимптотические методы и специальные функции/Ф. Олвер. -М.: Наука, 1978. -375 с.
- Михлин, С.Г. Линейные уравнения в частных производных/С.Г. Михлин. -М.: Высшая школа, 1977. -431 с.
- Ильин, В.А. О разрешимости смешанных задач для гиперболических и параболических уравнений/В.А. Ильин//Успехи математических наук. -1960. -Т. 15, вып. 2 (92). -С. 97-154.
- Прудников, А.П. Интегралы и ряды/А.П. Прудников, Ю.А. Брычков, О.И. Маричев. -М.: Наука, 1981. -800 с.
- Лаврентьев, М.А. Методы теории функций комплексного переменного/М.А. Лаврентьев, Б.В. Шабат. -М.: Наука, 1973. -736 с.
- Деч, Г. Руководство к практическому применению преобразования Лапласа/Г. Деч. -М.: Наука, 1965. -288 c.
- Манжиров, А.В. Справочник по интегральным уравнениям/А.В. Манжиров, А.Д. Полянин -М.: Факториал Пресс, 2000. -384 с.


