О решении задачи маршрутизации транспорта с помощью подвижного генетического алгоритма

На российском рынке логистических услуг большая часть от всего объема рынка логистики приходится на транспортную логистику, поскольку на территории России имеется множество автомобильных (841 тыс. км), железных (86 тыс. км) дорог и воздушных путей (800 тыс. км). В связи с этим управление транспортными потоками является важнейшим элементом логистики, при этом по некоторым оценкам применение современных подходов позволит снизить общие экономические издержки в среднем на 15-35 %, а транспортные расходы - примерно на 25 % [2]. При планировании поставок возникает задача построения оптимального маршрута для набора транспортных средств, которые должны посетить множество заданных объектов.

Например, для снабжения сети магазинов со склада с помощью имеющихся автомобилей необходимо построить для них маршруты передвижения, оптимизировав суммарное преодолеваемое расстояние (для минимизации расходов на транспортировку) и/или время доставки товаров.

Такая задача хорошо известна в теории графов и называется задачей маршрутизации транспорта. Задача является NP-трудной, поэтому на практике для ее решения применяют различные приближенные и эвристические алгоритмы, в том числе генетические алгоритмы (ГА) [3].

Исследования, касающиеся генетических алгоритмов, ведутся уже сравнительно давно, но и в настоящее время развиваются достаточно активно. В частности, в последние годы появилось такое новое направление, как подвижные генетические алгоритмы [4-6]. Учитывая специфику задачи маршрутизации транспорта и сложную структуру, описывающую решение задачи, интересным представляется исследование возможности построения подвижного генетического алгоритма для решения этой задачи.

Таким образом, цель данной статьи -исследовать возможность решения задачи маршрутизации транспорта с помощью подвижного генетического алгоритма, проанализировать скорость работы такого алгоритма, качество получаемого решения, а также сравнить его с другими существующими подходами.

1. Постановка задачи

Для начала формализуем решаемую задачу в терминах теории графов.

Пусть

V = { v о , v i , ..., v n } - множество вершин,

где v о - место начального расположения всех транспортных средств (депо или склад), v i , ..., v n - цели, которые необходимо посе

тить;

C = { C ij }, i , j е [0, N ] - квадратная матрица расстояний между вершинами, имеющая размерность N +1, где C ij - расстояние между

вершинами v i и v j ;

M - количество имеющихся транспорт-

ных средств;

R = { R i }, i е [1, M] - множество маршру-

тов     транспортных     средств,     где

R i = ( j i, o , j i,i , ., j i,k ) - маршрут i -го транспортного средства, представляющий собой после-

довательность номеров посещенных вершин, в которой первый и последний элементы равны нулю (j) о = jj ,k =0), что означает, что марш-

рут начинается и заканчивается в точке

начального расположения;

с ( R i ) = c

j, ,0 , j, ,1

+С

Ji ,1 , j, ,2

+ ... + c

J\ k — 1 , ^Jк k

длина маршрута, равная сумме расстояний между каждой парой соседних вершин в маршруте R i .

Входными данными в задаче является матрица расстояний C и количество транспортных средств M . Решением задачи является такое множество маршрутов R , что все це-

ли оказываются посещенными, а суммарная длина всех маршрутов является минимальной. Заметим, что посещение одной цели не-

сколькими транспортными средствами ведет только к увеличению общей длины маршрутов, поэтому будем считать, что каждая вершина входит ровно в один маршрут. Таким образом, на искомое множество R накладывается ограничение: для любой вершины v i , i е [1, N ], существует единственное j такое, что i е R j . Оптимизируемая величина определяется следующим образом:

M

F = £ C ( R j ) ^ min .       (1)

j = 1

Другим вариантом оптимизации в сформулированной задаче является минимизация не суммарной длины маршрутов, а мак-

симальной из длин, что будет соответствовать оптимизации времени на доставку всех товаров. В этом случае оптимизируемая величина определяется так:

F ‘ = max C ( R ) ^ min . (2) j e ! M ] j

• 2.    Подвижный генетический алгоритм

• 2.1.    Первый вариант кодирования

В классическом генетическом алгоритме, описанном в [3], каждое решение кодируется одной хромосомой, представляющей собой перестановку на множестве чисел от 1 до N . Такая перестановка определяет последовательность посещения вершин, но не содержит разделения на маршруты. Решить задачу оптимального разбиения последовательности на маршруты можно, например, методом динамического программирования за время O(N ■ M ) . Таким образом, хромосома в таком алгоритме не кодирует явно одно допустимое решение, а является, по сути, промежуточным представлением, позволяющим впоследствии построить решение за полиномиальное время.

В разработанном подвижном ГА применен аналогичный подход с использованием промежуточного представления, однако хромосома хранит не саму перестановку, а предрасположенность к превращению в ту или иную перестановку. Рассмотрим два варианта кодирования.

В первом варианте перестановка представляется в виде кода факториального представления ее порядкового номера. Для получения такого кода каждый элемент перестановки необходимо заменить его порядковым номером в упорядоченном списке чисел, составленных из элементов перестановки, чьи позиции не меньше текущего.

Например, кодом перестановки (4, 5, 1, 3, 2) является код (4, 4, 1, 2, 1). У данного кодирования есть два преимущества: простота кодирования и раскодирования, а также возможность использования стандартного одноточечного оператора кроссинговера. Элементы кода перестановки обладают следующим свойством:

MaxVal i <  N - i + 1, 1 <  i <  N (3)

где i - позиция в коде перестановки, а MaxVal i - максимальное значение элемента на позиции i .

Хромосома в генетическом алгоритме будет представлять собой матрицу P = { p j }, i , j е [1, N] , где p ij - вероятность того, что ген на позиции i будет равен j . Свойство (3) позволяет хранить хромосому в виде треугольной матрицы. Кроме того, для вероятностей, очевидно, должно выполняться условие, что сумма всех вероятностей для каждой позиции равна 1, то есть

N - i + 1

V i : X P j = 1 . (4) j = 1

При вычислении приспособленности вначале матрица вероятностей трансформируется в код перестановки ( i -й элемент кода принимает значение j с вероятностью p ij ). Затем по коду строится сама перестановка. Наконец, приспособленность особи вычисляется на основе формул (1) или (2). Поскольку в генетических алгоритмах большей приспособленности должны соответствовать более хорошие решения, приспособленностью особи будем считать значение, обратное к F (или F ‘ ).

При выполнении генетических операторов они применяются не только к самой хромосоме (матрице вероятностей), но и к соответствующему коду перестановки. После выполнения генетического оператора вероятности для каждой позиции i < N пересчитываются по следующему алгоритму.

Пусть в коде перестановки на позиции i после выполнения оператора находится значение j . Тогда элемент матрицы p ij необходимо увеличить, а все остальные ненулевые элементы i -й строки уменьшить. Вначале определяется предельная величина изменения

D i = ma^x( p j + n ind ,1 ^— n DR ) ^— P j , ⁽⁵⁾

где Пш — индивидуальная скорость обучения, n_DR — коэффициент разнообразия (гиперпараметры подвижного ГА).

Далее определяется предельная величина уменьшения каждого элемента:

^di ⁼

D i

,       1 ’

СЛ^ — 1

где cnt i – это количество ненулевых элементов в i -й строке.

Затем все остальные (находящиеся не в столбце j ) ненулевые элементы i -й строки матрицы уменьшаются на величину

^ ik = P k - min P k - ^di, V dr ), k = 1.. N - i + 1, k ^ j

Наконец, элемент pij увеличивается на величину л , =   Z 4 .        (8)

k = 1.. N - i + 1, k ^ j

Такой алгоритм пересчета гарантирует сохранение свойства (4) для матрицы вероятностей.

Рассмотрим пример. Пусть N =4, Ппd = 0.12, Пои = 0.08 , хромосома непосред-

ственно после применения оператора имеет " 0.1 0.3  0.4 0.2' вид P = 0.5 0.2  0.3 0.4 0.6 , а соответ- . 1 2 ствующий код – (3, 1, 2, 1). Тогда для позиции i=1 имеем: j=3, D1=0.12, d1=0.04, ^ = 0.02, ^2 = 0.04, ^4 = 0.04, Л= 0.1 и после корректировки первая строка матрицы P примет вид (0.08, 0.26, 0.5, 0.16). Для остальных позиций алгоритм аналогичен.

• 2.2.    Второй вариант кодирования

Во втором варианте код перестановки не используется. Хромосома так же представляет собой матрицу вероятностей P = { p ij }, i , j e [1, N , но p ij здесь означает вероятность того, что i -й элемент самой перестановки равен значению j . При таком подходе возникает ряд проблем. Например, возникает необходимости следить за корректностью перестановки. Данная проблема решается следующим образом. При формировании перестановки на основе хромосомы будем хранить список уже использованных номеров.

Тогда значение в текущей позиции не может быть равно ни одному значению из этого списка.

Пусть A ( i ) – список доступных значений для позиции i .

Пересчитаем вероятность каждого из доступных значений по формуле

P * = P ij , (9)

где S_; = Z p^ , и выберем одно из доступ- j e A ( i )

ных значений в соответствии с этими вероятностями.

Таким образом, будет получена корректная перестановка. Далее все особи отсортируем в порядке увеличения приспособленности.

Для лучших особей пересчитаем их хромосомы по формулам (5)–(8) аналогично тому, как это описано выше для первого варианта при применении генетических операторов.

Для худших особей их хромосомы также будут пересчитаны аналогично, но с точностью до знака (будем уменьшать вероятность появления соответствующих значений).

Результаты

Оба описанных выше варианта были реализованы в виде компьютерной программы на языке C++. Исходный код программы находится в открытом доступе1.

Для сравнения также была использована существующая реализация классического генетического алгоритма ² . Для небольших размерностей входных данных ( N < 12) также выполнялось сравнение с точным переборным алгоритмом.

Тестирование проводилось на 7 тестах, со значениями гиперпараметров п_пd = 0-05 , n_DR = 0.005 .

Данные значения были подобраны экспериментальным путем. Время работы классического ГА на каждом тесте было ограничено 10 секундами. Для подвижного ГА было установлено минимальное количество итераций для завершения – 1000; в случае достижения этого количества время работы ограничивалось также 10 секундами.

Число особей в популяции после отбора было равно 60. Результаты исследования первого варианта реализации подвижного ГА приведены в таблице.

Сравнение первого варианта реализации подвижного ГА с другими алгоритмами

N	Точный алгоритм	Классический ГА		Подвижный ГА (первый вариант кодирования)
	Сум-мар-ная длина ( F )	Сум-мар-ная длина ( F )	Количество итераций	Сум-мар-ная длина ( F )	Коли-че-ство итераций
5	2395	2395	4508046	2395	1164
10	2354	2354	3627050	2354	1000
20	-	1416	2835683	4782	1000
40	-	2136	1528882	13753	1000
60	-	2039	872248	19488	1000
80	-	2152	546916	27304	1000
100	-	2125	353726	36993	1000

Как видно из таблицы, при N ≤10 оба ГА находят точные оптимальные решения. Однако при N >20 подвижный ГА работает значительно хуже классического.

Дальнейший анализ результатов показал, что в подвижном ГА не наблюдается стабильного роста средней приспособленности популяции, иными словами, алгоритм не сходится даже к точке локального экстремума. Одна из причин может заключаться в том, что очень похожие коды, кодируемые хромосомами, порождают совершенно разные перестановки.

Например, коды (4, 2, 1, 1) и (1, 2, 1, 1) отличаются всего одним значением, но при этом кодируют очень разные перестановки (4, 2, 1, 3) и (1, 3, 2, 4) соответственно. Одна из этих перестановок может иметь высокую приспособленность, за счет этого она будет чаще участвовать в операциях скрещивания, вероятность появления соответствующего кода будет увеличиваться. Однако при этом повышается и вероятность появления другого кода, порождающего совсем другую перестановку с возможно очень низкой приспособленностью. В результате средняя приспособленность популяции может не измениться или даже стать меньше.

Еще один фактор, на который можно обратить внимание – подвижный ГА работает значительно медленнее классического.

Как видно из таблицы, при N ≥10 за 10 секунд не успевают завершиться даже 1000 итераций, в то время как количество итераций классического ГА оказывается на несколько порядков больше.

Результаты работы второго варианта реализации подвижного ГА оказались лишь на 10 % лучше первого варианта, хотя из анализа графика (см. рисунок) следует, что средняя приспособленность популяции достаточно стабильно растет.

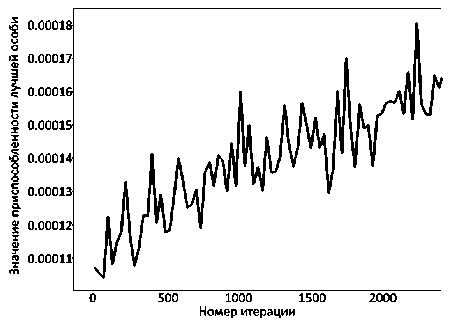
Зависимость приспособленности лучшей особи в популяции от номера итерации для второго варианта кодирования

По всей видимости, в данном случае решающим становится ограничение в 1000 итераций, которых попросту не хватает для достижения экстремума.

Заключение

Проведенные исследования позволяют утверждать, что применение подвижных генетических алгоритмов для решения задачи маршрутизации транспорта, возможно, и дает корректные результаты. При количестве целей N ≤10 подвижный ГА позволяет получить точное решение.

Однако при больших значениях N алгоритм работает слишком медленно, получаемые результаты оказываются значительно хуже результатов классического ГА. Выбор способа кодирования существенно влияет на результаты работы.

Таким образом, дальнейшие исследования могут быть направлены на оптимизацию подвижного ГА, рассмотрение других способов кодирования и пересчета вероятностей, а также применение дополнительных оптимизационных эвристик.