О решениях для внутренних захваченных волн с условиями прилипания на стенке

Для решения задач динамики Мирового океана применяются нелинейные математические модели [1], описывающие широкий спектр движений — баротропные и бароклинные волны Россби, инерционно-гравитационные волны, экваториальные и береговые волны Кельвина и другие. В большинстве случаев решение таких задач может быть найдено только с применением современных численных методов и мощных компьютеров. Исследование теоретическими методами возможно лишь в рамках подсистем, описывающих тот или иной физический процесс в бассейне с упрощенной геометрией. Теория позволяет оценить характерные пространственно-временные масштабы процессов, из чего следуют, например, условия, налагаемые на шаги сетки, и методы дискретизации задачи.

Важную роль в динамике областей океана, примыкающих к материковому склону, играют волны Кельвина [2], которые принадлежат к типу волн, захваченных вращением Земли у вертикальной стенки. Отметим, что при построении моделей динамики океана узкий шельф и резкий материковый склон часто заменяют вертикальной стенкой. В работе [3] исследовано влияние вертикальной вязкости на внутренние волны Кельвина. В

работе [4] представлены результаты исследования совместного влияния вертикальной и горизонтальной вязкостей на волны Кельвина, длина которых превышает радиус деформации Россби.

Основной целью данной работы является получение и исследование решений для захваченных волн, длина которых не превышает радиус деформации Россби. Изложен вывод уравнений и представлены решения для захваченных волн в модельном бассейне с плоским дном и одной прямой вертикальной стенкой.

2.    Основные уравнения

Рассмотрим несжимаемую вязкую жидкость, находящуюся в бассейне с плоским дном и одной прямой вертикальной стенкой. Будем пользоваться правой декартовой системой координат (х, y, z) с направленной вверх осью z и началом координат на невозмущенной поверхности. Пусть состояние покоя характеризуется плотностью р ₀ (z) и давлением p ₀ (z) . Запишем в приближениях Буссинеска и гидростатики систему основных уравнений теории океанских течений [5], линеаризованную относительно основного состояния покоя:

atu * - fv * = -р-1а хР * + ц(а xxu * + а yyu * )+а z (Ka zu *), a * + fu * = - р-1а yp * + ц (axxV * + a yyv *) + az (Ka zv *),

• d    zp * = - g р*,

at р* + w *а z р0 = о, a w* + а u* + а v* = 0.(5)

zxy

Здесь и далее: t — время; и * , v * , w * — компоненты вектора скорости; Z — отклонение уровня жидкости от невозмущенного положения; p , р — отклонения давления и плотности от их невозмущенных значений; р _* — характерное значение плотности; f — параметр Кориолиса, полагаемый постоянным; g — ускорение свободного падения; H — глубина бассейна, H > 0 при х <  0; ц , K — коэффициенты горизонтальной и вертикальной турбулентной вязкости [5], полагаем ц > 0; N — частота Брента-Вяйсяля; d F — частная производная функции F по переменной 5 . Следует отметить [1], что приближение гидростатики может быть принято для крупномасштабных движений, в которых горизонтальный масштаб гораздо больше вертикального и становится несправедливым при рассмотрении тех движений, где необходим учет коротких внутренних волн. Запишем граничные условия на поверхности с учетом малости Z :

p*| = р*gz       w*| = дЛ-< z=0l

Зададим условия непротекания и прилипания на стенке и 1 .=0 = v 1 х=0 = 0(7)

и условия непротекания и свободного скольжения на дне w 1    =0,     a zu 1    = az v 1    =0.(8)

Iz=-H                   z lz=-H      z lz=-H- '

Оценка влияния трения о дно на внутренние захваченные волны выполнена в работе [3] на примере двухслойной жидкости. Показано, что в уравнениях движения для нижнего слоя трение о дно дает вклад в результирующий коэффициент трения. Отношение вклада трения о дно к вкладу трения между слоями равно rH 1 ²/( r H ²), где H 1 — толщина верхнего слоя, r и г' — коэффициенты трения о дно и между слоями соответственно. Далее полагаем, что глубина H настолько превышает толщину термоклина, что влиянием трения о дно можно пренебречь. Исключая р из (3) при помощи (4), имеем

- 1 А * _{Л т} 2 * р * 8 tz p = N w ,

где

N ² = ^- g P^- 1 ^d z Р о -

Известно [5], что структура уравнений (1), (2), (5), (9) позволяет искать решение задачи в виде:

и *= р»1 P (z) u (x, y, t),       v *= р*1 P (z) v (x, y, t);(11)

w*= - W(z)dt П(x, y, t);(12)

p * = P (z )П( x, y, t).(13)

Подставляя (11)-(13) в (5), запишем это уравнение как

81П   = 5 и + 5, v xy Р =        = -s2,                                                              (14) р,а zW где sn — постоянная разделения переменных. Рассмотрим простой случай [3], когда произведение KN2 является постоянной величиной. Подставив (11)-(13) в (1), (2), (9) с учетом (14) и краевых условий (6), (8), имеем где

8tu - fv = -sn2 8xn + ц (axxu + 8yyu) - du,5 tv + fu = -s „2 8 y n + ц (a xxv + 5 yyv)- dv,

d,n + d и + 8, v = 0,

txy

_Й d P P н 8_Z — ' ~ = 0, zN ² s 2

н = 0, zH

d_z P + P

N ^{2 z}

= 0, z=0

d = KN ²/ s ² _n , П = ^{n / s} 2 •

Совокупность собственных функций P_n(z) задачи (18), (19) обладает свойством полноты [5]. Введем безразмерные переменные согласно соотношениям:

T = ft,    X = x /Ln,     Y = yILn;(22)

U(X, Y, T) = u(x, y, t)/ en,   V(X, Y, T) = v(x, y, t)/ en,    h(X, Y, T) = n(x, y, t);(23)

Ln = f .(24)

Здесь L_n — радиус деформации Россби внутренней моды с номером n . Перепишем в безразмерных переменных уравнения «мелкой воды» (15)-(17) и краевые условия (7)

5 TU - V = -5 Xh + E (5 XXU + 5 YYU)- DU,(25)

5 TV + U = -5 Yh + E (5 XXV + 5 YYV)- DV,(26)

dTh id XU id YV = 0,(27)

U |x=0=0, V |x=0=0,(28)

где

E = -£-, D = d.(29)

fLnf

3. Захваченные волны

Обозначим через c, X и l = 2 nd безразмерную фазовую скорость, длину волны и волновое число соответственно; расстояние, на которое смещается гребень волны за время, пока амплитуда уменьшается в e раз, есть

Re ( c ) Im ( c ) l

Пусть { U m , ^V m , ^h m ^} , гЛе

IT = IT ^A ikmn^^ ⁺ i^{l ( Y cT} )

Um Ume          , h => A ikmX+il(Y-cT)

ⁿm me ^e           ,

Im( c )<0,   Im( k m ) < 0,

V = V ^A e‘im^{X + lI ( Y cT} ) m m                 ,

являются решениями системы уравнений (25)-(27). Решения типа волн, захваченных вращением у стенки, будем искать в виде:

( U , V , h ) = ( U 1 + U ₂, V 1 + V , , h 1 + h ₂ ) ,            Im( k 1 )>Im( k ₂).

Для решений вида (34) краевые условия (28) выполняются при

U A + U ₂^a=0,      V 1 ^A + V ₂^a = 0.

Перепишем уравнения (25)-(27), подставив выражения для U , V и h из (31) и (32):

(а + e к ² - icAlU A - V A + ikh A =0     ( m = 1,2),

m            m m m m

UA +(a + sк2 -ic\lVA + ilhnA=0      (m = 1,2), m              m            m n, /, lchA - kUA - lVA = 0                  (m = 1,2), m m m m                                     \, /, где а = D1l + El,    e = E1l.

Исключим h m из (36)-(38), а из полученных уравнений исключим U A и V ₂ ^A при помощи (35); в результате имеем:

( ( ( e k 1 ² + а ) c - ic ² ) l ² + ik^ ) U A + ( ik 1 - c ) lV 1 ^A =0, (40) ( ( ( e к ₂ ² + а ) c - ic ² ) l ² + ik ₂ ² ) U 1 ^A + ( ik ₂ - c ) lV 1 ^A=0, (41) ( c + ik 1 ) U A + ( ( e k А + а ) c + i ( 1 - c ² ) ) /V/ 0, (42) ( c + ik ₂ ) U A + ( ( e k ₂ ² +а ) c + i ( 1 - c ² ) ) V/ 0. (43)

Для существования нетривиальных решений системы уравнений (40)-(43) необходимо задать три условия. Запишем сначала условия существования нетривиальных решений для четырех систем уравнений, состоящих из [(40), (41)], [(42), (43)], [(40), (43)] и [(41), (42)] соответственно; это дает

( 1 - il ² c e ) k1 k ₂ + ( i + l ² c e ) c ( k1 + k ₂ ) + ( c + i а ) cl ² =0,

i e ck 1 k ₂ + e c ² ( k 1 + k ₂ ) - c ² - ic а + 1 = 0,

[( i -L / ²^c) ² -I- (in 4-^4- il²p\^ — A\lr²4-(n — f^²7^{2 2}-|_T²]_i- 11 i l c e ) e ck 2 I i cx + c + il e ) c 1 1 k 1     ( cx ic ) e c l I k 1 + k 2 ) +

+ k1 k ₂ + ic ( k ₂ - k 1 ) - l ² c ⁴ - 2 il ² а c ³ + ( l ² а ² + 1 + l ² ) c ² + il ² а c = 0,

4- 12r-e\pr-k 2 -I-     -I- с -I- il 2f)^ Й 2 -I- (n — iA^^2!2 ( b-2 4- b- 2\ 4- i (i +1 ce) eck 1 + (iex + c + il e) c 1 pc2 (^а ic) ec l (k1 k2 ) +

+ k 1 k ₂ + ic ( k1 - k ₂ ) - 1 ² c ⁴ - 2 il ² а c ³ + ( l² а ² + 1 + 1 ² ) c ² + il ² а c = 0.

Первую пару условий преобразуем, умножив (44) на c ² e , а (45) — на ( i + l ² c e ) c , а затем взяв сумму и разность полученных соотношений; во второй паре вычтем (47) из (46). Имеем

2ec (1 - icel2)k 1 k2 + 212c3e + (i + 2ie12а)c2 - (а + el2) c - i = 0,(48)

2(i + cl e)ec (k1 + k2) — ic +(el +а)c + i = 0,(49)

(cl 2e + i + c а-ic2)(k1 + k2)-2 c = 0.(50)

Исключая k 1 + k 2 из (49), (50), получим уравнение для c:

(1 - 4г2l2)c4 + i2 (l2г - 2г + a) c3 - (l4г2 + 2 + 2l^a + a2) c2 - i2 (l2г + a) c +1 = 0; (51)

исключая k 1 или k 2 из (48), (49), получим уравнение для k:

2(i + cl2г)гc2k2 + (i - ic2 + (гl2 + a)c)k -

—2iгl c +(21 га +1) c + i (l г + a) c — c — 0,      k e{k 1, k2}, решения которого имеют вид k1,2

—i + ic — (l г + a) c ± ^JM। 2M2

где

M 1 — (ca + i +12cг - ic2) - 8( l2cг + i )гc3 (ica -1 + c2 + 212c2гa- 2il2c3 г + il2c8) ,(54)

M 2— 2( l2 c г + i )г c2,(55)

M 1 ^ 0,     M2 ^ 0.(56)

Уравнения (51) и (52) и есть искомые условия существования нетривиальных решений системы (40).

Можно показать, что решения уравнений (51) и (52) удовлетворяют уравнениям (2.7) и (3.4) работы [4]:

г k4 (1 - il2 c г) + k2 (a- ic + г l2 (1 - 2 ic (a- ic )))-

- ic + ( a- ic ) l ² ( 1 - ic ( a- ic ) ) — 0,               k e { k 1 , k ₂ } ,

1 + ic г ( k 1 + k ₂ ) 2 ( 1 - il ² c г ) — 0.

Подставив в (57) и (58) выражения для k 1 и k 2 из (53) и применив второе условие из (56), получим факторизованные уравнения, в которых один из сомножителей совпадает с левой частью уравнения (51).

Пусть H = 1 км, f = 10^-4 с^-1, K = 0,01 м²с^-1. Выберем два значения коэффициента горизонтальной турбулентной вязкости из рассмотренных в работе [6]: Ц 1 — 10³ м²с^-1 и ц ₂ — 10² м²с^-1. Оценим порядок величин a и г и относительную роль вертикальной и горизонтальной составляющих турбулентной вязкости в случае внутренней волны с X * — 25 км при L — 50 км, N — 10^-2 с^-1. Из (22) следует, что l — 2 п L / X * , где l « 12. Подставляя приведенные выше числовые значения и р — 10³ м²с^-1 в (20), (29) и (39), имеем D « 4^10^-4, E « 4-10^-3, a « 5^10^-2, г « 340^-4. Аналогично, при ц — 10² м²с^-1 имеем D « 4-10^-4, E ~ 4-10^-4, a ~ 5-10^-3, г ~ 3-10^-5. Поскольку a = D/l+El « El , при данных условиях влиянием вертикальной турбулентной вязкости можно пренебречь.

Решения уравнений (51) и (52), удовлетворяющие условиям (33), представлены на рисунке 1 для трех наборов параметров D и E . Графики функций Re(c), Л , Re(k) и Im(k),

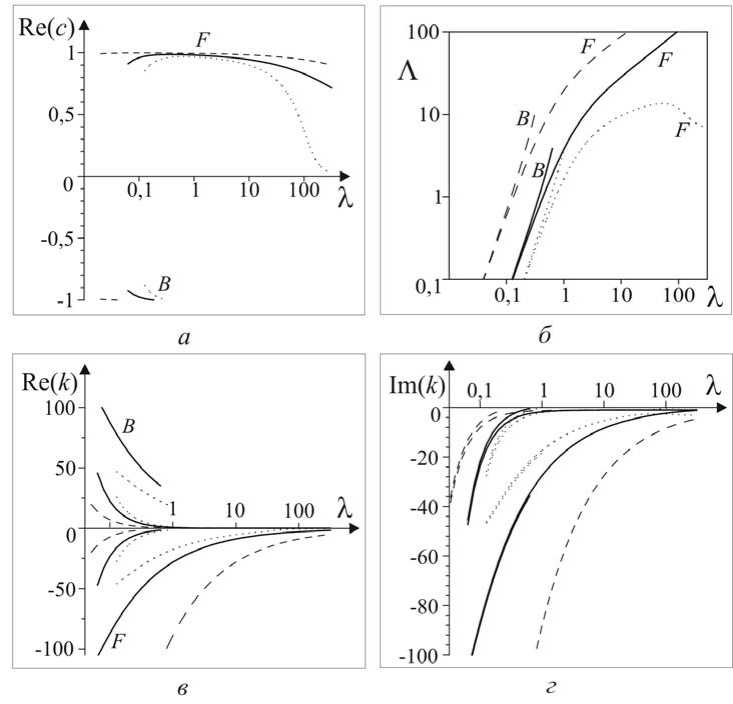
Рис. 1. Графики функций, зависящих от λ : а — Re( c ); б — Λ ; в — Re( k ); г — Im( k ) (сплошные линии — D = 4 ∙ 10^-4, E = 4 ∙ 10^-3; штриховые линии — D = 4 ∙ 10^-4, E = 4 ∙ 10^-4; пунктирные линии — D = 0,1; E = 0,01)

зависящих от λ , показаны на рисунках 1, а–г соответственно.

Отметим, что на рисунке 1 не показаны решения с Λ < 0,02. Решения для волн с длиной больше радиуса деформации Россби ( λ > 1) получены и проанализированы в работе [4]. Важными особенностями решений в области волн c λ < 1 являются существенное уменьшение масштаба убывания захваченных волн с уменьшением длины волны и наличие волн с отрицательной действительной компонентой фазовой скорости c . Здесь и далее решения с Re( c ) > 0, соответствующие волне Кельвина, помечены символом F , решения с Re( c ) < 0 — символом B .

На рисунке 2 представлены два решения уравнений (25)–(27) с граничными условиями (28), полученные при λ = 0,6; D = 4∙10^-4; E = 4∙10^-3. Решения нормированы на максимальные значения h max = 1; ( U B ) max ≈ 0,21; ( V B ) max ≈ 1,03; Λ B ≈ –3,4; ( U F ) max ≈ 0,19; ( V F ) max ≈ 0,95; Λ F ≈ 1,7. На рисунках 2, а и г показаны изолинии h B и h F с шагом 0,2; на рисунках 2, б и д — U B и U F с шагом 0,05; на рис. 2, е — V B и V F с шагом 0,2. Изолинии с положительными значениями показаны сплошными линиями, с отрицательными значениями — штриховыми линиями, с нулевым значением — пунктиром. Следует отметить наличие тонких пограничных слоев на рисунках для U и V и существенное различие масштабов убывания для решений F и B .

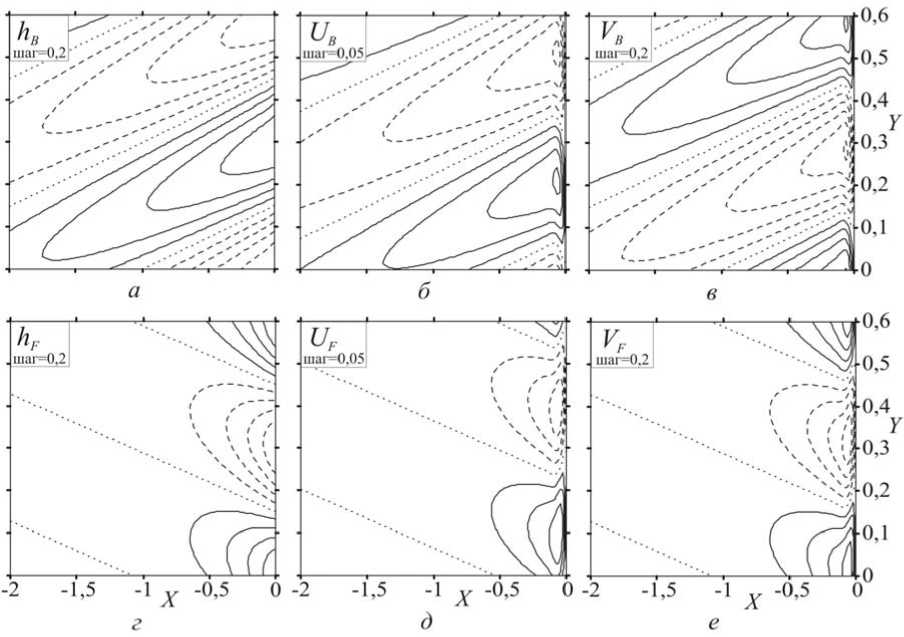
Рис. 2. Изолинии h , U и V при X = 0,6; D = 4 - 10-⁴; E = 4 ^ 10 -3

(сплошные линии — положительные значения; штриховые линии — отрицательные значения; пунктир — нулевые значения).

4.    Асимптотические решения

Полагая, что £ является малым параметром, будем искать приближенные решения в виде асимптотических рядов:

c = c(0) + £1/2c(1) + £c(2) + £3/2c(3) +... ,(59)

k1 = k^ + £1/2k1(1) +£k^ + £3/2k1(3) + ... ,(60)

k2 =£-1/2k20) + k21) +£1/2k22) +£k23) +... .(61)

Подставляя (59)–(61) в уравнения (48)–(50) и приравнивая к нулю коэффициенты при разных степенях £ , получим последовательность уравнений для определения c ⁽⁰⁾, k 1 ⁽⁰⁾, k ₂ ⁽⁰⁾ и так далее. Положив £ = 0 в (59) или (60), получим уравнение

(0)2

c -1 + i a c = 0, решениями которого являются

(0) F

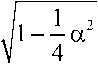
- i a , 2

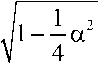
- i a .

Необходимо отметить, что рассматривается та ветвь функции квадратного корня, которая отображает плоскость c разрезом вдоль отрицательной действительной полуоси на правую полуплоскость. Для k2(0) имеем квадратное уравнение k20)2 - ic(0) + a = 0

и для него выбираем такие решения уравнения (64), которые удовлетворяют условию (33):

k20)=k20) I ™    =-1 V2—a - i1 v2+a,

2f     2 c(0) = c?)     22

k2°) = k2°)I     ™ =1V2 — a — i1V2 + a.

2в     2 c(0)=c0 2             2

Остальные переменные можно выразить через с (0) и k2(0). Например, k - ic(0),

₍₀₎ i + a c ⁽⁰⁾      k (1) = (^a 4 ^{- 4 a} 2 ^{+ 2} ) ^{ic (0) + 3 a-a} 3

² 2 ic ⁽⁰⁾ -a ,    ²          ( 4 -a ² )( 1 - i a c ⁽⁰⁾ )

Асимптотические решения для волны Кельвина получены в работе [4] и проанализированы при X > 1. Для k ₁ ⁽¹⁾ запишем приближенное выражение, полагая a <1:

(1)        (0) (0) 2

Л-1     ^,* i *v2 c It

B lB

2 1/3

E 1/3 ,

^X в

2п

l B

« пE1/322/3.

Необходимо отметить важную роль второго слагаемого в приближенном решении k ^{( a )}

1F для волны Кельвина, обеспечивающего существенное уменьшение масштаба убывания с уменьшением длины волны. Графики |Im k(X)| (Рис. 3) построены в логарифмических координатах при D = 4∙10-4 и E = 4∙10-3. Вертикальные штриховые линии пересекают горизонтальную ось в точках с координатами Х|Л = 0,1 » 0,12, Xв « 0,8 и X|s = 0,1 * 160. Исключены из рассмотрения короткие волны с длиной X < Х|Л = 0,1, которые быстро затухают. Решениям k1 и k2 уравнений (51) и (52) соответствует пунктир, приближенным решениям k(a) = k1(0) + s1Z2k(1) и k2a) =£-1/2k20) + k21) — сплошные линии. Отметим, что в области относительно коротких волн графики для k1(a) и k2(a) практически совпадают с графиками для k1 и k2.

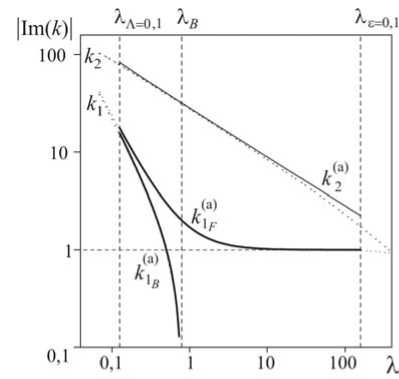
Рис. 3. Функции |Im k ( λ )| для k 1 и k 2 (пунктир), k 1 ^(a) и k 2 ^(a) (сплошные линии)

5.    Заключение

В работе рассмотрены решения для внутренних волн, захваченных вращением Земли у вертикальной стенки в бассейне с плоским дном. Система уравнений для захваченных волн приведена к удобному для решения виду: уравнение четвертой степени (51) для фазовой скорости волны c и квадратное уравнение (52) для волновых чисел k 1 и k 2 . Обратные значения мнимых частей k 1 и k 2 характеризуют масштабы экспоненциального убывания для захваченной волны и для пограничного слоя соответственно. В области относительно коротких волн ( λ < 1) решения характеризуются следующими важными свойствами: 1) масштаб убывания волн Кельвина существенно уменьшается с уменьшением длины волны; 2) имеется второе решение в виде волны противоположного направления (Re( c ) < 0). Построены асимптотические решения для c, k 1 и k 2 , применимые для относительно коротких волн, и получена оценка (69) для λ B — верхней границы диапазона длин волн второго решения.

Результаты работы полезны для анализа решений в численных моделях динамики океана, построенных в приближении гидростатики. По-видимому, представляет интерес исследование решений для захваченных волн в рамках более полных моделей.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 09-01-98519) и ДВО РАН (проект № 06-III-A-03-072).