О риссовской суммируемости непрерывных функций из классов Никольского со смешанной нормой
Автор: Созанов Валерий Гаврилович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 2 т.4, 2002 года.
Бесплатный доступ
Для непрерывной функции из класса Никольского со смешанной нормой установлена равномерная сходимость на компактах средних Рисса спектрального разложения функции к самой функции.
Короткий адрес: https://sciup.org/14318052
IDR: 14318052
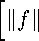
Список литературы О риссовской суммируемости непрерывных функций из классов Никольского со смешанной нормой
- Алимов Ш. А., Ильин В. А. I. Условия сходимости спектральных разложений, отвечающих самосопряженным расширениям эллиптических операторов. II. Самосопряженное расширение оператора Лапласа с произвольным спектром//Дифференц. уравнения.-1971.-Т. 7, № 5.-С. 851-882.
- Алимов Ш. А. О разложимости непрерывных функций из класса Соболева по собственным функциям оператора Лапласа//Сиб. мат. журн.-1978.-Т. 19, № 4.-С. 721-734.
- Козлова Н. Н. О риссовской суммируемости непрерывных функций из классов Никольского//Дифференц. уравнения.-1984.-Т. 20, № 1.-С. 46-56.
- Созанов В. Г. О равномерной сходимости спектральных разложений из H^{\alpha}_{(p_1,p_2)}//Дифференц. уравнения.-1984.-Т. 20, № 1.-С. 124-128.
- Бесов О. В., Ильин В. П., Никольский С. М. Интегральные представления функций и теоремы вложения.-М.: Наука, 1975.
- Никольский С. М. Об одной задаче С. Л. Соболева//Сиб. мат. журн.-1962.-Т. 3, № 6.-С. 845-851.
Статья научная
