О роли математики в социальной и правовой сферах общества

Математика по праву считается самой древней наукой, созданной для познания мира, в том числе посредством создания математических методов и моделей.

Современные разделы математики исследуют непрерывность, случайность, графические обозначения и доказательства, а также процесс передачи информации.

Более того, математическое моделирование стало основным методом изучения социальных процессов.

Между тем некоторые математические модели и методы можно использовать в исследовании социальных процессов.

Автор анализировал работы отечественных ученых-математиков и юристов, среди которых работы А. Пуанкаре, Н. Бурбаки, П.С. Краснощекова, В.С. Нерсесянца, а также социологов М. Вебера, К. Маркса, И. Канта.

Основу современных научных исследований составляют междисциплинарные исследования. Кроме того, междисциплинарные исследования, как правило, используют методологию других наук.

В настоящей работе предлагается использовать методологию математики в исследовании социальных и правовых объектов.

С.В. Игнашов отмечает, что «математика служит цивилизационным двигателем развития культуры, определяющим темпы и глубину процессов рационализации и модернизации культуры» [1, с. 10].

Математика, будучи универсальным языком науки, является ключом к познанию социальных явлений. Кроме того, математика позволяет создать более эффективные правовые модели регулирования общественных отношений.

Например, П.С. Краснощеков создал модель социального поведения людей, которые действуют в социальной группе [2, с. 77].

Между тем, как правило, в гуманитарных и социальных науках математический метод уступает свое место непосредственному анализу явлений, поэтому использование математического аппарата сводится главным образом к созданию математических моделей социальных процессов.

Н. Бурбаки отмечали, что «в своей аксиоматической форме математика представляется скоплением абстрактных форм - математических структур, и оказывается (хотя по существу и неизвестно почему), что некоторые аспекты экспериментальной действительности как будто в результате предопределения укладываются в некоторые из этих форм» [3, с. 10].

Например, по нашему мнению, математическая топология и теория хаоса могут описать некоторые закономерности социальных процессов.

Топология, будучи разделом математики, изучает систему множеств в их непрерывности. Основоположником топологии является А. Пуанкаре, который связал математику с качественными характеристиками объектов [4, с. 84].

Другими словами, топология описывает феномен непрерывности.

В математическом аспекте социальные объекты можно рассматривать как математические множества.

Что же такое множество? Как множества взаимодействуют друг с другом? Множество – это набор абстрактных объектов (рис. 1). Например, в социальном аспекте множеством является индивид, социальная группа и общество.

О. Конт понимал под обществом функциональную систему, включающую в себя государство, классы и семью [5, с. 73].

Важно отметить, что множества могут сочетаться друг с другом. Например, элементы одного множества могут быть элементами другого множества (рис. 2).

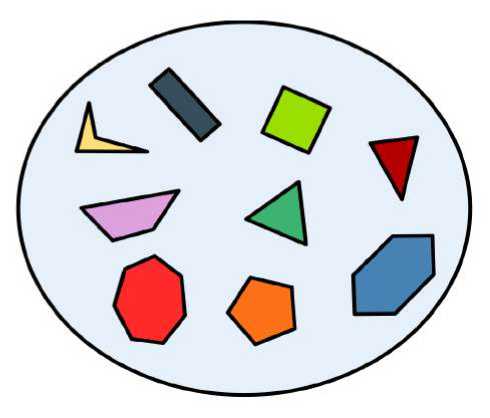
Рис. 1 – Множество

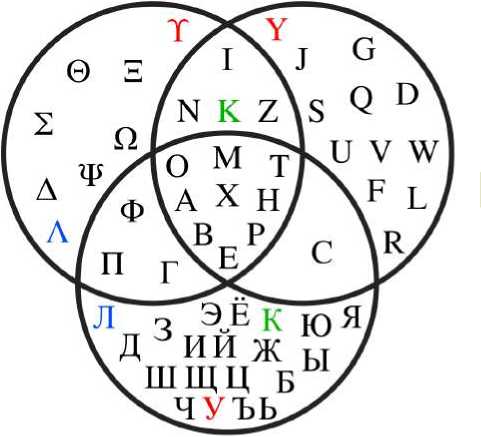
Рис. 2 – Сочетание множеств

Так, члены одной социальной группы могут одновременно являться членами другой социальной группы.

Например, личность является членом множества социальных групп и всего общества.

Важно отметить, что в топологии имеет место такое явление, как гомеоморфизм.

Так, согласно гипотезе А. Пуанкаре, всякое односвязное компактное трехмерное многообразие без края гомеоморфно трехмерной сфере (рис. 3) [4, 109].

Иными словами, гомеоморфизм – это постоянная непрерывная связь объектов, которая позволяет переносить свойства одного объекта на другой.

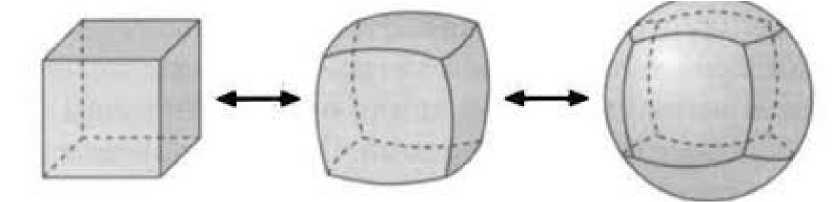
Рис. 3 – Гомеоморфизм сферы

Гомеоморфизм является свойством, отражающим непрерывную связь объектов.

Топологическая связь объектов можно выразить математическим языком. Например: два объекта хиY называют гомеоморфными, если существует непрерывное взаимно однозначное отобра-f. у__^ у жение          , причем обратное отображение          тоже непрерывно.

Таким образом, свойства одного пространства сохраняются при трансформации его в другое пространство.

По нашему мнению, феноменом гомеоморфизма можно описать непрерывную связь человека, социальной группы и общества.

К. Маркс определял общество как особый социальный организм, «сумму связей и отношений, в которых индивиды находятся друг в друге» [6, с. 13].

Ф. Теннис разработал систему о социальных отношениях и социальных связях. По мнению Ф. Тенниса, основу общества составляют общественные связи [7, с. 45].

М. Вебер рассматривает общество как взаимодействие людей, являющееся результатом социального действия [8, с. 69].

К. Маркс отмечал, что «человек – не абстрактное, где-то вне мира ютящееся существо. Человек – это мир человека, государство, общество» [6, с. 414].

Н.К. Михайловский отмечал, что «человек есть частица более высокого целого – общества, критерий и цель прогресса – сам человек, человек – не средство, а результат, цель» [9, с. 73].

Более того, топология выделяет топологически несовместимые объекты. Топологическую несовместимость объектов можно продемонстрировать с помощью петли.

Например, воображаемую петлю на сфере можно затянуть, а на торе нельзя (рис. 4).

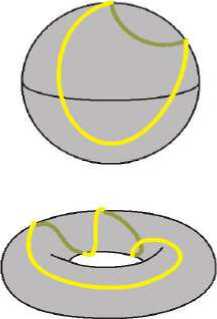
Рис. 4 – Стягивание петли

Между тем в социальном аспекте, по нашему мнению, можно выделить топологически несовместимые социальные объекты, например, государство и общество.

Важно отметить, что методологию исследования диссипативных структур можно успешно использовать в социальной сфере.

Общество является диссипативной структурой, в которой отношения между людьми и социальными группами можно условно обозначить как траектории.

Что же такое диссипативная структура? По мнению И. Пригожина, «диссипативные структуры – это открытые системы, которые обмениваются энергией (результатами работы) или информацией с внешней средой [10, с. 187].

Важно отметить, что в диссипативных структурах особую роль играет странный аттрактор.

Что же такое «странный аттрактор»? «Странный аттрактор» – это нетривиальное притягивающее замкнутое инвариантное множество, лежащее в фазовом пространстве системы внутри поглощающей области, в которую входят все траектории, пересекающие границу этой области (рис. 5).

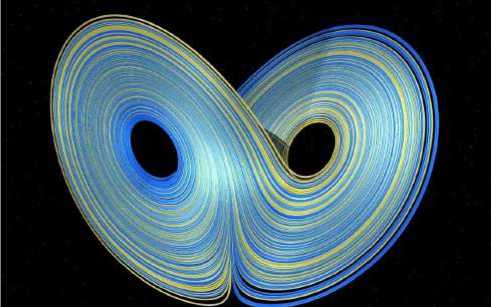
Рис. 5 – Странный аттрактор

Важно отметить, что странный аттрактор представляет собой математическую модель развития открытой системы.

Свойством странного аттрактора является то, что он притягивает все возможные траектории.

Между тем, по нашему мнению, в социальном аспекте эффект притяжения можно обусловить биосоциальной природой человека.

Т. Добжанский отмечает, что «биологическая и социальная подсистемы в человеке с этой точки зрения понимаются как взаимозависимые (interdependent), находящиеся во взаимодействии (interaction) измерения» [11, с. 286], [5, с. 286].

Кроме того, К. Маркс и Ф. Энгельс отмечали, что «человек не есть абстрактная сущность. Он является, с одной стороны, закономерным результатом эволюции природы, а с другой, как личность обладает субъективностью, сознательно-деятельностным свойством, активно воздействует на окружающий мир и изменяет его в соответствии со своими взглядами» [12, с. 91].

Таким образом, можно сделать вывод, что на поведение человека оказывает влияние как социальная, так и биологическая составляющие его природы.

Важно отметить, что право, будучи универсальным регулятором общественных отношений, устанавливает формальные рамки, которые, по нашему мнению, совпадают с границей странного аттрактора, рассматриваемого в социальном аспекте.

Другими словами, в социальном аспекте границы странного аттрактора представляют собой математические границы свободы личности.                       311

В.С. Нерсесянц справедливо отмечал, что «право – это математика свободы» [13, с. 119].

Другими словами, право и математика имеют дело с моделированием действительности.

Таким образом, математическая модель странного аттрактора позволяет описать вектор эволюции социальной системы, обусловленной социальными и биологическими предпосылками, следовательно, открывают возможность для совершенствования правового регулирования общественных отношений.

В заключение необходимо отметить, что использование методов математики в социальной сфере, с одной стороны, позволит с математической точностью описать социальные процессы, с другой – создать эффективные правовые модели, регулирующие общественные отношения.