О самоорганизации и профилировании кристаллов кварца в условиях неравновесной термодинамики

Самоорганизация и хаос – это основные структурные характеристики процесса кристаллизации. В них проявляется противоборствующий характер тенденции к порядку в условиях неравновесной термодинамики. В представленной работе с этих позиций рассматривается формирование кристаллов кварца, которые выращивали в автоклавах – сосудах высокого давления в содовом растворе в неравновесных термодинамических условиях: в нижней зоне автоклава размещался исходный материал – шихта, а в верхней с более низкой температурой – затравочные кристаллы. В зоне растворения шихты раствор насыщается кристаллообразующим веществом, которое в растворе находится в беспорядочном состоянии. Под действием разности температур и плотности раствор перемещается из зоны растворения в зону роста, где он становится пересыщенным. Избыток вещества выделяется из раствора, попадает на поверхность затравочного кристалла, диффундирует и встраивается в его решетку в определенном порядке. Проявляются два процесса: диффузионный, определяющий доставку вещества к кристаллу, и кинетический, обуславливающий встраивание вещества в решетку кристалла.

Система кристалл – раствор открытая и происходит поглощение энергии извне. Оба процесса, растворение и кристаллизация подчиняются второму началу термодинамики, который определяет вероятность протекания процесса и связан с энтропией: в зоне растворения энтропия возрастает, а в зоне роста уменьшается. Согласно уравнению Больцмана изменение энтропии в процессе кристаллизации пропорционально отношению термодинамических вероятностей кристалла и раствора:

Wk

A A = k In -k .

W p

Формирование кристалла на затравочных кристаллах проходит в две стадии: регенерации и собственного роста. На стадии регенерации нарастание кристалла проходит с большой скоростью по плоскостям с высокой поверхностной энергии, в частности с - ( 0 0 0 1 ) , +п -

(1 1 2 0), -n - (1 1 2 0), s - (1 1 2 1) и x - (1 5 6 1). Пирамиды регенерационных поверхностей постепенно вытесняются гранями с минимальной поверхностной энергией R – (1 0 1 1), r - (0 1 1 1). В дальнейшем формирование проходит нарастанием по медленнорастущим граням ромбоэдров. Нарастанием по ромбоэдрам и граням тригональной призмы формируются грани гексагональной призмы (1 0 1 0); кристалл принимает стационарную фор- му.

Скорость роста кристалла пропорциональна изменению энтропии. Согласно [1, 2] dS

—= adV, dt где

j a dV - полный

поток энтропии по всему объему системы. Учитывая, что с т =

;1 Е x i y , где

Т - температура, x i - движущая сила, y i - поток массы. В свою очередь, x i = Ац , где

Ац = цр - цк - разность химических потенциалов кристаллообразующих частиц в растворе и на растущей поверхности кристалла, в (Р, Ф) — кинетический коэффициент встраивания частиц в решетку кристалла, ρ и ϕ – полярные координаты растущей поверхности. Получим уравнение

a = T Т вАТ 2 •

Для поверхностей, нарастающих на стадии регенерации, коэффициенты встраивания частиц в решетку имеют большую величину, а потому переход от неупорядоченного расположения частиц в растворе в упорядоченное состояние в кристалле на стадии регенерации проходит с большой скоростью. В этом проявляется первый принцип Ле-Шателье, когда система стремится быстрее сбросить энергию [2].

Следовательно, скорость роста кристалла и поток энтропии зависят от коэффициента β – встраивания частиц в решетку на поверхности кристалла, состояние которой определяется кристаллографической ориентировкой и величиной Ат . Значение в можно определить из уравнения в = —Vy , где Ар - разность плотностей кристалла и раствора, А с ® /АТ - пересыщение Ас раствора, ν – скорость роста грани.

Из [5] следует, что предельная скорость нарастания по грани (0 0 0 1) составляет 0,4 мм/сут, по грани +n – 0,2 мм/сут, по –n – 0,15 мм/сут. Нарастание по граням стационарной формы: по (1 0 1 1) в 5,5 раз, по (0 1 1 1) в 5,6 раз, и по грани (1 0 1 0) в 11 раз меньше, чем по грани (0 0 0 1). Тогда при Ар ® 2 г/см3, А Т = 10 и / ® 3-10-3 г/см3 получим следую щие значения: вс ~ 3 "10 5 см/с, eR ~ 6 "10 6 см/с, вт ~ 3 "10 6 см/с. Нарастание по граням ста- ционарной формы роста проходит со скоростью на порядок ниже, чем по поверхностям стадии регенерации.

Для потока с незначительным отклонением от стационарного состояния имеем:

5adV = 0, т. е.      = min, dt2

где δ – знак вариации. Полная скорость производства энтропии с учетом, что при постоянной скорости роста увеличение поверхности пропорционально квадрату времени, составляет [2]

dS=t '" f Л e d ( р . Ф )•

В процессе роста скорость производства энтропии возрастает и кристалл должен приобрести форму с минимальной поверхностной энергией, препятствующую скорости возрастания энтропии. В этом случае подынтегральное выражение уравнения должно стремиться к минимуму.

У кристаллов кварца в процессе регенерации формируются поверхности с гранями мини- мальной поверхностной энергией R - (1

0 1 1), r - (0 1 1 1) и m - (1 0 1 0), которые устойчивы к изменениям условий роста. Следовательно, при отклонении системы от стационарного состояния в ней возникают изменения, возвращающие систему в прежнее состояние согласно второму принципу Ле-Шателье.

Полученное выражение для изменения скорости энтропии в процессе роста кристалла является аналогом уравнения Гиббса–Кюри для равновесного состояния системы кристалл – раствор, определяющим конечную форму роста кристалла:

Т aiSi = min, V = const, где σ – удельная поверхностная энергия, S – площадь соответствующей грани, V – объем кристалла. Преимущество уравнений неравновесной термодинамики в том, что они отражают последовательность формирования внешней формы кристаллов с переходом от неустойчивой формы к устойчивой.

Образование стационарной формы роста лежит в основе самосовершенствования и профилирования кристаллов.

В случае зарастания внутренних полостей кристалла подынтегральное выражение должно стремиться к максимуму, принимая вид [4]:

Брызгалов А.Н., Фалькова О.Н., Ахметшин К.Ф.

О самоорганизации и профилировании кристаллов кварца в условиях неравновесной термодинамики dS dt

t^ fjj в d (p, ф).

Таким образом, внешняя форма кристаллов ограничивается плоскостями с минимальной поверхностной энергией, а внутренняя полость зарастает поверхностями с максимальной скоростью роста.

Профилирование внешней формы кристаллов кварца и зарастание полостей

Рассмотрим несколько ( 0 0 0 1 ) .

случаев формирования кристаллов на плоской затравке среза

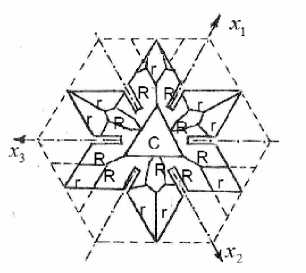
Рис. 1. Формирование кристалла в виде шестиконечной звезды, контуры которой совпадают с

пассивными гранями ( 1 0 1 о )

• 1.    Из пластинки среза ( 0 0 0 1 ) вырезана затравка в виде шести лучевой звезды, контуры которой совпадают с плоскостями ( 1 0 1 0 ) . На поверхности пластинки выполнены надрезы по трем направлениям параллельно пассивным граням ( 1 0 1 0 ) . В результате поверхность затравки разделится на ромбовидные ячейки, каждая из которых в процессе роста будет формироваться независимо от других гранями ромбоэдров (рис. 1).

• 2.    Используется затравка в виде кольца. Нарастанием по граням тригональной призмы +n и – n кристалл в плоскости

Вырезано шесть полостей параллельно граням m . По мере роста кристалла три полости в положительном направлении оси х за счет трапецоэдра ( 1 5 6 1 ) зарастают.

а)

б)

Рис. 2. Заращивание кристалла в форме кольца: а) начальный этап заращивания; б) конечный этап заращивания

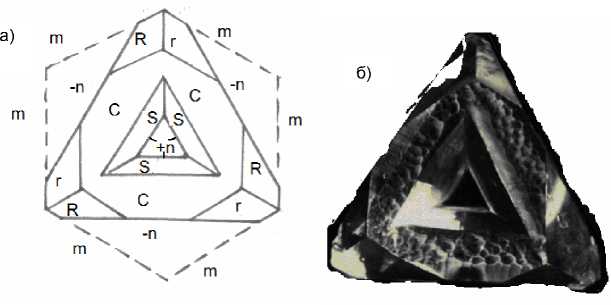
Рис. 3. Формирование кристалла на затравке треугольной формы: а) схематичный рисунок; б) внешний вид

( 0 0 0 1 ) приобретает гексагональную внешнюю форму с гранями m, к которым примыкают грани r и R .

Во внутренней полости кристалла образуются грани тригональной призмы +n и – n , к которым примыкают грани s и x . По мере роста кристалла полость постепенно зарастает активными гранями (рис. 2). Таким образом, внешняя форма кристалла образована гранями стационарной формы с минимальной поверхностной энергией, а внутренняя полость зарастает гранями с высокой поверхностной энергией.

3. Затравка имеет треугольную форму. Внутренние стороны

затравки совпадают с гранями +n , а внешние с –n . Скорость на-

растания по внутренним граням в 1,3 раза больше, чем по внешним. На внутренние грани опираются

активные поверхности дипирамиды s - ( 1 1 2 1 ) . Нарастанием по граням отрицательной

тригональной призмы - n формируются пассивные грани m - ( 1 0 1 0 ) и гексагональная форма кристалла. На внутренние поверхности опираются грани трапецоэдра х . Внутренняя полость кристалла постепенно зарастает нарастанием по активным поверхностям +n и x (рис. 3).

Таким образом, внешняя форма кристалла независимо от геометрической формы затравки на последней стадии формируется медленнорастущими гранями, а внутренняя полость зарастает бы- строрастущими гранями.