О счётности простых деревьев и следствиях из неё
Автор: Чечулин Виктор Львович
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Математика
Статья в выпуске: 4 (4), 2010 года.
Бесплатный доступ
Ввиду доказанной ранее некорректности диагонального метода (Зенкин) переобоснованы, посредством семантики самопринадлежности, теоремы Гёделя, а также утверждения о несчетности количества точек прямой; указано на возможность лишь счетного количества обозначений, построен пересчет обозначений n-ичных разложений чисел на отрезке [0, 1).
Семантика самопринадлежности, теоремы гёделя, предикативные и непредикативные формальные системы, несчетность числа точек на прямой, счетность обозначений
Короткий адрес: https://sciup.org/14729683
IDR: 14729683 | УДК: 519.50
Текст научной статьи О счётности простых деревьев и следствиях из неё
1. Предисловие
В 1997 г. Зенкиным А. А. были опубликованы результаты [1], показывающие некорректность диагонального метода Кан-тора1. В связи с этим возникает потребность в анализе и переобосновании базирующихся на этом диагональном методе утверждений, что и представлено ниже, с использованием семантики самопринадлежности, введенной русским математиком Миримановым еще в 1918 г. [2].
С одной стороны, приведено описание краткого варианта доказательств теорем Гёделя, с другой – в теории множеств с само-принадлежностью разрешен аналог контину-ум-гипотезы.
2. Краткое доказательствотеорем Гёделя
Подробно основания структур с само-принадлежностью и сами эти структуры опи- саны в работах [3], [4], для понимания этого параграфа достаточно интуитивного представления о несамопринадлежащих, X∉X, и самопринадлежащих, Y∈Y, объектах.
Теоремы Гёделя доказываются достаточно кратко. Пусть имеется предикативная теория Т такая, в которой есть набор аксиом (схем аксиом) А i , и выводимые утверждения В j , (A i1 , …, A in , В j1 ,..., В jm ) |= В j0 , (1)
причем это выводимое утверждение не содержится в цепи вывода от аксиом до себя самого, т. е. в левой части формулы (1), которую, безотносительно ее содержания, обозначим через L, {A i1 , …, A in , В j1 ,..., В jm } = L, В j0 ∉ L.
Теорема 1. В предикативной системе не доказуема ее непротиворечивость.
Теорема 2 (о неполноте). Предикативная теория не полна.
Схемы доказательств этих теорем одинаковы: непредикативные утверждения о непротиворечивости, или полноте, предикативной теории Т не являются в ней выводимыми ввиду того, что эти утверждения в их выводе ссылаются на себя самих
Пусть С – высказывание о непротиворечивости теории, т. е. в С утверждается, что все утверждения теории Т таковы, что в этой теории не выводимы и их отрицания. И пусть
Т непротиворечива, т. е. высказывание С выполнимо на всех высказываниях этой теории (важным для использования семантики самос-сылочных высказываний является допущение того, что это высказывание уже истинно), т. е. семантически C выводимо из множества всех высказываний теории, в том числе и из себя самого (раз отрицает собственное отрицание при наличии непротиворечивости),
{A i , …, В j , …, С} |= С, (2)
доказана теорема.
Теорема 3 (о предикативных системах). Непротиворечивость и полнота предикативной теории не доказуемы средствами самой этой теории. □
Таким образом, без применения диагонального метода передоказаны теоремы Гёделя. Поскольку в этих теоремах (1–3) не упоминался совершенно тип логики, посредством которого осуществляется вывод в теории Т, то
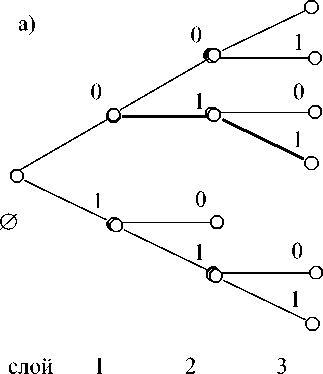
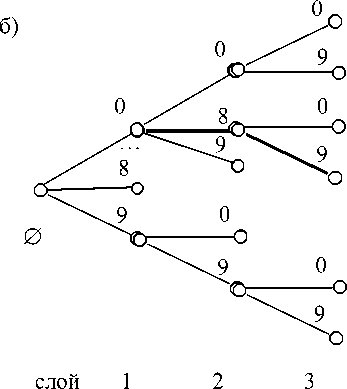
Рис. 1. Фрагменты 2-дерева (а), и 10-дерева (б)
C ∈ L, что противоречит условиям предикативности системы Т (C ∉ L). Следовательно, теорема 1 о том, что в предикативной теории не доказуема ее непротиворечивость, доказана. □
Пусть F – высказывание о полноте системы; F утверждает, что в системе Т выводимы все утверждения, в том числе и само F, но тогда F, если оно верно, семантически (самос-сылочно) тем самым высказывается о себе самом:
{A i , …, В j , …, F} |= F, (3) F ∈ L, что противоречит условиям допущения чисто предикативности теории Т (F ∉ L). Доказана теорема 2. □
Однако предположение о непредика-тивности теории Т являлось лишь начальным условием рассуждений, и в связи с доказанными теоремами 1, 2 допускается и иная ин-тепретация результата – непротиворечивость теории не доказуема в предикативных системах, т. е. доказательства непротиворечивости возможны только с допущением непреди-кативности (самоссылочности) в семантике рассуждений, как, например в теории множеств с самопринадлежностью [3]. Тем самым эти теоремы действенны на множестве предикативных теорий с произвольными правилами вывода (в т. ч. на использующих многозначную, модальную и т. п. логики).
Следующие утверждения, рассматриваемые без использования диагонального метода, связаны с отношением счетности и несчетности множеств.
3. Несчетность точек на прямой
При описании упорядоченных структур в теории множеств с самопринадлежно-стью в работе [4] было показано, что объекты, определяющие структуру прямой, само-подобны, т.е. обладают свойством структурной изоморфности объекта его собственному подобъекту.
Определение 1 . Два объекта структурно изоморфны, если они изоморфны и совпадают по структуре, т. е. А ≅∈ В, если А ≅ В (изоморфизм ϕ : A → B) и если для любых а1, a 2 ∈ A, ϕ (а 1 )=b 1 , ϕ (a 2 )=b 2 , b 1 , b 2 ∈ B, имеет место (а 1 ∈ a 2 ) ⇔ (b 1 ∈ b 2 ).
Определение 2. Внутренность объек- та А содержит объекты, принадлежащие объекту А, за исключением самого объекта А;
V(А)={[х] ∈ М |([х] ∈∅ или ([x] ∈ А и А ∉ V(А))}.
Определение 3. Объект А собственно внутренний по отношению к объекту В, если он принадлежит В, но не принадлежит ряду внутренностей объекта В.
Определение 4. Объект самоподобен, если он структурно изоморфен подобъекту, собственно внутреннему по отношению к этому же объекту.
Для самоподобных объектов C и D одной прямой, D ⊂ С, или С ⊂ D, или D = С, причем в любом случает имеет место структурный изоморфизм D ≅∈ C. Для объектов натурального ряда (натуральных чисел) свойство структурной изоморфности, очевидно, не выполняется, одни натуральные числа другим неизоморфны. Следовательно, самоподобные объекты несчетны.
Теорема 4. Количество точек на прямой несчетно. □
Точкам на прямой соответствует максимальный упорядочиваемый отношением принадлежности объект – нить недостижимых последователей, являющаяся самоподобной (см. [4], [5]).
4. Счетность количества обозначений
Очевидно также, что, располагая конечным алфавитом, можно иметь не более чем счётное количество обозначений (конечной длины). Множество подмножеств конечного множества конечно. Счетное повторение этой операции для начального конечного множества дает счетное множество.
Даже в случае, если имеется счетный алфавит, но сами обозначения содержат конечное число символов, итоговое количество обозначений счетно (ввиду счетности множества конечных подмножеств счетного множества).
Таким образом, следует различать точки на прямой (как показано выше, их несчетное количество) и их десятичные обозначения, которых, по означенным выше соображениям, счетное количество. Остается построить пересчет этих обозначений, не используя диагональный метод.
5. Счетность простых деревьев
Представления чисел на отрезке [0, 1) в n-ичной системе счисления (c m разрядами) изоморфны n-дереву (глубины m), что очевидно. На рис. 1а выделенная линия соответствует двоичному обозначению числа 0,011…, на рис. 1б – десятичному обозначению 0,089…. (номер слоя соответствует порядковому номеру цифры за запятой).
Пересчет n-дерева организуется следующим образом: при обходе считается 1-й слой, затем – 2-й, затем – 3-й и т. д. В m-дереве для всякой вершины r-го слоя ее номер не более чем nr. Для всех n и r из N nr < N, из чего следует счетность количества вершин дерева (и счетность его ветвей, имеющих начало в 0-м слое), а значит, и счетность количества n-ичных обозначений чисел на отрезке [0, 1).
Таким образом, несчетность множества точек на прямой и счетность количества n-ичных обозначений чисел на отрезке [0, 1) согласуются друг с другом. Доказана теорема.
Теорема 5 (о счетности обозначений). Количество k-ичных (k ∈ N ) обозначений чисел на отрезке [0, 1) отличается от количества точек на прямой на этом отрезке (несчетного) и является счетным. □
Из этой теоремы следует естественный вывод, что не все изучаемые множества можно обозначить (на все изучаемые объекты обозначений не хватит, поскольку этих объектов мысли гораздо больше, чем счетное количество обозначений). Такое истолкование теоремы согласуется с интуитивными представлениями и поэтому является естественным.
6. Заключение
Как показано выше, классические утверждения (теоремы Гёделя, утверждения о несчетности числа точек на прямой) доказуемы без диагональных рассуждений, в семантике самопринадлежности.
Счетность же количества обозначений, счётность количества n-ичных обозначений чисел на отрезке [0, 1), не противоречит тому, что объектов мысли (точек на прямой) несчетное число, – не все из существующего (мыслимого) можно обозначить.
Список литературы О счётности простых деревьев и следствиях из неё
- А. А. Принцип разделения времени и анализ одного класса квазифинитных правдоподобных рассуждений (на примере теоремы Г. Кантора о несчетности)//Доклады Академии наук. 1997. Т.356, №6. С.733-735.
- Френкель А., Бар-Хиллел И. Основания теории множеств/пер. с англ.; под. ред. А.С. Есенина-Вольпина. М.: Мир, 1966. 366 с.
- Чечулин В.Л. О множествах с самопринадлежностью//Вестн. Перм. ун-та. Сер. Математика. Механика. Информатика. 2005. Вып. 2(2). С.133-138.
- Чечулин В.Л. Об упорядоченных множествах с самопринадлежностью//Вестн. Перм. ун-та. Сер. Математика. Механика. Информатика. 2008. Вып. 4(20). С.37-45.
- Чечулин В.Л. О свободе теории множеств с самопринадлежностью от известных парадоксов наивной теории множеств//Вестн. Перм. ун-та. Сер. Математика. Механика. Информатика. 2010. Вып. 1 (1). С. 29-31.


