О сходимости масштабируемого алгоритма построения псевдопроекции на выпуклое замкнутое множество

В распознавании образов имеет большое значение задача сильной отделимости, которая состоит в нахождении слоя наибольшей толщины, разделяющего два выпуклых непересека-ющихся многогранника. Такая задача может быть решена с помощью итерационного метода, использующего операцию проектирования. Однако на практике применение этого метода существенно ограничивается тем, что далеко не всегда удается построить конструктивную формулу для вычисления проекции точки на выпуклое множество. Поэтому целесообразно заменить операцию проектирования последовательностью фейеровских отображений [1]. Указанный метод был описан в работе [2].

При решении практических задач экономико-математического моделирования часто встречаются задачи с большим количеством переменных и ограничений. Подобные задачи при решении требуют значительных вычислительных мощностей. В связи с этим актуальной является задача разработки параллельного алгоритма разделения выпуклых многогранников с помощью фейеровских отображений, допускающего эффективную реализацию на многопроцессорных системах с массовым параллелизмом. В методе решения задачи сильной отделимости на базе фейеровских отображений наиболее ресурсоемкой частью является алгоритм вычисления псевдопроекций на многогранник. В данной работе предлагается новый масштабируемый алгоритм построения псевдопроекции на выпуклое замкнутое множество и доказывается его сходимость.

Статья состоит из трех частей. В первой части описывается численный метод решения задачи сильной отделимости на базе фейеровских отображений. Во второй части приводится новый масштабируемый алгоритм построения псевдопроекции на многогранник. В третьей части доказывается сходимость предложенного алгоритма.

1.    Численный метод решения задачи сильной отделимостина базе фейеровских отображений

Пусть даны два выпуклых непересекающихся многогранника M С R n и N С R n , заданные системами линейных неравенств:

M = { x | Ax <  b } = 0 ;

N = { x | Bx <  d } = 0 ;                                 (1)

M П N = 0 .

Задача сильной отделимости – это задача нахождения слоя наибольшей толщины ( π -слоя), разделяющего M и N . Сильная отделимость, по существу, эквивалентна задаче отыскания расстояния между M и N в смысле метрики

p ( M,N )=min{ | x — y | |x G M, y 6 N }.                      (2)

Если x G M и y G N являются arg-точками задачи (2), то есть p ( M, N ) = | x — y | , то слоем наибольшей толщины, разделяющим множества M и N , является P = xc x G P i П P 2}, где P i и P ₂ - полупространства, задаваемые линейными неравенствами

(x — X, X — y) <  0 и (y — y,X — y) >  0 .

Задача сильной отделимости может быть решена с помощью известного итерационного метода последовательного проектирования [2].

Если множества M и N достаточно просты в смысле простоты реализации операции проектирования точек на них, то такой метод решения задачи сильной отделимости может быть использован на практике. Но если M и N – произвольные многогранники, то такой подход не может быть признан эффективным, так как не известен универсальный конструктивный метод построения проекции точки на многогранник. Ситуацию можно исправить, если вместо операции проектирования использовать фейеровские отображения.

Рассмотрим итерационный метод решения задачи сильной отделимости на базе фейе-ровских отображений.

Дадим определение фейеровского отображения. Пусть ^ G {R n ^ R n} . Отображение называется M -фейеровским, если выполняются следующие два условия:

v ⁽ y ) = y, ^ y ^G M ;

! ^(x) — y | <  | x — y | , V y G M, V x G M.

Сконструируем M -фейеровское отображение, следуя работе [3]. Представим систему линейных неравенств, задающих многогранник M , в следующем виде:

Ax <  b : l j (x) = ( a j ,x ) — b j , j = 1,..., m ,                              (3)

где a j = 0 для любого j . Определим l + (x) следующим образом:

l j + (x) = ^max{ l j (x), 0 } , j = 1,..., m .                                    (4)

Тогда отображение вида l+(x)

^ ^{( x )} = x - i a X j     a                             (5)

будет M-фейеровским для любой системы положительных коэффициентов {aj > 0}, m j = 1,..., m, таких, что ^2 aj = 1 и коэффициентов релаксации 0 < Xj < 2. Аналогичным j=i образом сконструируем N -фейеровское отображение ψ . Используя отображения ϕ и ψ, мы можем построить следующий алгоритм F, решающий задачу сильной отделимости с использованием фейеровских отображений.

Алгоритм F . Пусть задано произвольное начальное приближение z g G R n . Зафиксируем положительное вещественное число ε . Алгоритм состоит из следующих шагов:

Шаг 0. к := 0 .

Шаг 1. X k +i := lim ^ u ( z k ) .

Шаг 2. y k+i := lim <( z k ) .

u →∞

Шаг 3. z k+i := x k +i + y k +l .

Шаг 4. к : = к + 1 .

Шаг 5. Если min {| x k +1 — X k ||, ||у к +1 — У к ||} >  е , перейти на шаг 1.

Шаг 6. Стоп.

Алгоритм F был исследован в работе [4]. Проведенные вычислительные эксперименты на модельных и случайных задачах подтвердили его эффективность. Однако, для больших размерностей работа алгоритма F требовала значительного времени. Например, при размерности задачи n = 512 время счета на одном процессорном ядре составило 16 часов. В связи с этим возникла необходимость разработки параллельной версии этого алгоритма для многопроцессорных систем с массовым параллелизмом. Очевидно, что в алгоритме F ресурсоемкими являются шаги 1 и 2. На каждом из этих шагов реализуется последовательный фейеровский процесс, в результате которого мы получаем псевдопроекцию точки на многогранник. Многогранник, задаваемый системой линейных неравенств, всегда является выпуклым замкнутым множеством. В следующем разделе мы предложим новый масштабируемый алгоритм построения псевдопроекции точки на выпуклое замкнутое множество с использованием фейеровских отображений, который допускает эффективное распараллеливание на большом количестве процессоров.

2.    Масштабируемый алгоритм S построения псевдопроекции

В основе масштабируемого алгоритма построения псевдопроекции на выпуклое замкнутое множество лежит метод разбиения вектора на подвекторы. Для каждого подвектора организуется независимый фейеровский процесс. Через каждые s шагов результаты, полученные на подвекторах, соединяются в один вектор, для которого считается невязка. Если значение невязки меньше заданного положительного числа ε , то полученный вектор принимается в качестве псевдопроекции. В противном случае вычисления продолжаются.

Дадим формальное описание алгоритма построения псевдопроекции на выпуклое замкнутое множество с помощью фейеровских отображений, допускающего эффективное распараллеливание на большом количестве процессорных узлов.

Введем следующие обозначения. Для произвольного линейного подпространства P С R ⁿ через п р (х) будем обозначать ортогональную проекцию x G R n на линейное подпространство P . Везде далее линейное подпространство мы будем называть просто подпространством.

Через p(P, x) := min ||p

— x | будем обозначать расстояние от точки x до подпространства P .

Пусть линейное многообразие L получается из P сдвигом на некоторый вектор z : L = P + z .

Через n L (x) будем обозначать ортогональную проекцию x G R n на линейное многообразие

L :

п ь (ж) = n p (x) + z.

Теперь мы готовы к формальному описанию алгоритма.

Алгоритм S. Пусть задано однозначное M-фейеровское отображение p G {Rn ^ Rn}, M -выпукло и замкнуто. Зададим разбиение пространства Rn в прямую сумму ортогональных подпространств: Rn = Pi ® ... ® Pr, Pi ± Pj при i = j. Для каждого подпро странства Pi (i = 1,..., r) построим линейное многообразие Li следующим образом. Пусть xi G Arg min p(Pi,x). Положим zi = n-i (xi) G P£ Здесь P^ обозначает ортогональное x∈M                                Pi           ii дополнение к подпространству Pi . Построим линейное многообразие Li путем сдвига подпространства Pi на вектор :i:

Li = Pi + Г.

Для каждого i G { 1,...,r } определим отображение

Pi(x) = nLi (p(nLi(x))) •

Зафиксируем некоторое натуральное число s и положительное вещественное число ε . Зададим произвольное начальное приближение x q G R n . Алгоритм состоит из следующих шагов:

Шаг 0. k := 0 .

r

Шаг 1. x k +i := £ (p - (x k ) — z i) .

i =1

m

Шаг 2. d := £ l + (x k +i ) .

j =i

Шаг 3. k := k + 1 .

Шаг 4. Если d >  e и || x k +i — x k || = 0 , перейти на шаг 1.

Шаг 5. Стоп.

На шаге 2 вычисляется невязка d , которая определяет степень близости точки x k +i к выпуклому замкнутому множеству M .

• 3.    Cходимость алгоритма S

Для доказательства сходимости нам понадобится следующая теорема, показывающая, что каждое отображение p i G {L i ^ L i}, строящееся в алгоритме S , является фейеровским относительно множества L i П M .

Теорема 1.

Пусть задано выпуклое замкнутое множество M С R n и однозначное M -фейеровское отображение p G {R n ^ R n} . Пусть P - некоторое собственное линейное подпространство в пространстве R n , T = P ^x - ортогональное дополнение к подпространству P . Пусть x G Arg mi n p(P, x) . Представим x в виде суммы ортогональных векторов из подпространств P и T : x = n p (x) + n T (x) . Обозначим : = п т (т) G T . Построим линейное многообразие L путем сдвига подпространства P на вектор z : L = P + z . Определим отображение p l G {L ^ L} следующим образом:

P l ( x ) = n L (р(п ь (ж))} .                                     (9)

Положим

Ml = L П M .                              (10)

Тогда отображение ϕ L является M L -фейеровским.

Доказательство. Сначала покажем, что

P L (y) = У, V y G M l .                                  (11)

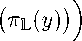
Пусть y G M l . Тогда, в силу (10), y G M. Так как отображение p является M -фейеровским, то p(y) = y . Учитывая, что y G L , отсюда получаем Р ь ( у ) = n L (p n L p p y)^ = n L (y) = y . Таким образом, условие (11) имеет место.

Теперь покажем, что

IIpl(x) — y\| < ||x — y||, Vy G Ml, Vx G Ml .

Пусть y G M l , x G L , x / M l . Из (10) следует, что в этом случае x / M . Так как отображение ϕ является M -фейеровским, то

\p(x) - у\\ < llx - y\\ •

Построим для p ( x ) и y их разложение в виде суммы двух ортогональных векторов, принадлежащих P и T соответственно:

p(x) = пр(p(x)) + nT(p(x)) , y = np(y) + г .

Подставляя эти разложения в (13), получаем l|np(p(x)) + nT(p(x)) - (np(y) + z) \| < \x - y\\ .

Сделав перекомпоновку, будем иметь

||(np(p(x)) - np(y)) + (nT(p(x)) - 2)1 < ||x - y\\ .

Замечаем, что (n p (p(x)) - n p (y)) G P и (n j (p(x)) - 2) G T — взаимно ортогональные векторы. В силу того, что квадрат нормы суммы ортогональных векторов равен сумме квадратов их норм, из (17) следует

IKp(p(x)) - My)!!2 + \nT(p(x)) - ^\2 < llx - y\2 •

В левой части неравенства стоит сумма двух неотрицательных слагаемых. Удалив второе из них, мы снова получим справедливое неравенство:

\\np(p(x)) - np(y)|2 < \\x - y\2 , откуда, в свою очередь, получаем

\ ⁿ P ⁽ P ^{( x )) - n} P ⁽ y) \ <  ^{| x -} y \\ •                                  ⁽¹⁹⁾

По построению L имеем пр(p(x)) = tl(p(x))-2. Подставляя это выражение в (19), получаем \nL(P(x)) - ^ - nP(y)! < |x - y\\ , или llnL(V(x)) - (пр(у) + z) II < llx - yh •                               (20)

Так как x 6 L , то x = n L (x) . Подставив в левой части неравенства (20) выражение n L (x) вместо x , получим

||ⁿL ⁽ V ^{( n} L ^{( x )))} - (^П Р ⁽ У) ⁺ ^ ¹ <  ||x - У ¹ .

С учетом (9) и (15), отсюда llVL(x) - У1 < IIх - У1 , то есть условие (12) справедливо. Теорема доказана.

Прежде чем приступить к доказательству сходимости алгоритма S , докажем следующую лемму.

Лемма 1.

Пусть { x k } - последовательность точек, порождаемых алгоритмом S на шаге 1:

xk+i := 2 (^(xk) - zi); k = 0,1,....

i =1

В условиях алгоритма S определим ML = Li П M. Положим xo = nLi(xO), xk+1 = Vi(xik) .

Тогда

^S(xk)= xS^(k+i), Vk 6 Z>o .

Доказательство. Доказательство проведем индукцией по k . Пусть k = 0 . В силу (8) имеем

V s ⁽ x o ) = V s ¹

Используя первое равенство из (22), получаем

V s ^{( x} o ⁾ = V s ¹ (ⁿ L i (^ ^{( x} 0

Так как x o 6 L i , то x o = n L i (^x o ) - Подставляя n L i (x o ) вместо x o в (24), получаем V s ⁽ x o ) = V s ^{- 1} (ⁿ L i (v(ⁿ L i (x o )))) .

С учетом (8), отсюда

VSW = _V S ( x O ) .

Применяя правое равенство из (22), отсюда получаем

^ S (x o )= vS^D .

Повторив эту подстановку еще (s — 1) раз, получим

Vi (xo) = xs , то есть база индукции имеет место. Пусть теперь k > 0. Рассмотрим тривиальное тождество

V s ^{( x} k ) = V s ^{( x} k ) •

В силу (21) X k : = (25), получаем

^ ^s (x k- i ) - zj^ . Подставляя

это значение в правую часть тождества

v s ^(x k ) = v s

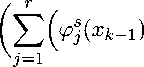
- zj

Отсюда по предположению индукции

vi⁽x k ) = v s

(e (vs^-D) j =i

- zj

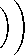
Это равносильно

v S ( x k ) = v S ^{- 1}

( v^E^xE - i))

- zj

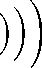
Используя (8), получаем

V ^{S (} x k ) = v s ¹

^ⁿ L i (v(ⁿ L i (Е ⁽ ?

x

j

s- ( k

i) ⁾

- zj

В силу (6) и (7) отсюда следует

V ^{S (} x k ) = v s ¹

(ⁿ L i (^ (Е^Ж^- Х) )

-

T j

Так как vs(xs^k-^) — zj ^ Pj (j = 1, • • •, r) и Pi^Pj при i = j, то из предыдущего получаем vS(xk) = vs 1 (nLi (v(vS(xS^(k—i))

-

z i + T

то есть vS(xk) = vs-1 (nLi (v(vS(xS^(k—i))))) •                            (26)

Из (8) следует vS(x^(k-1)) ^ Li, поэтому vS(x^(k-1)) = nLi (vS(xS^(k-1))) • Подставляя nLi(vs(xS^(k—i))) вместо vs(xS^(k—i)) в (N, получаем vS(xk ) = vs 1

^ⁿ L i (v(ⁿ L i (v s ^{( x} S^ ( k- 1)

В силу (8) отсюда получаем vs(xk) = vs 1 (vi (vs(xS^(k—i)))), или, что – то же самое vS(xk) = v2s(xS^(k-i)) •

Применяя правое равенство из (22), отсюда получаем vS(xk)= .2 X ) •

Повторив эту подстановку еще (2s — 1) раз, получим

Vs(xk) = xs-(k-1)+2s , то есть vs(xk ) = <(k+1), что и требовалось доказать.

Сходимость алгоритма S обеспечивается следующей теоремой.

Теорема 2.

Пусть { x k } - последовательность точек, порождаемых алгоритмом S на шаге 1:

x k+i := 2(^(x _fe ) — z i y, k = 0,1,....                        (27)

i=1

Тогда

{ X k } += ° 0 - x e R n .

Доказательство. В условиях алгоритма S определим

M L i = L i П M ( i = 1,...,r).

По теореме 1 отображение ϕ i является M L _i -фейеровским. Положим

^X 0 = ⁿ L i ^{( x} 0 ), ^x k+1 = V i ^(x k ) .                                   ⁽²⁸⁾

В силу непрерывности отображений π L _i и ϕ [3] отображение ϕ i – также непрерывно. Отсюда по лемме 39.1 [3] имеем

{ x k } + = 0 - X i e M L i , V i G{ 1,...,r } .                          (29)

Определим

X = 2 (x - — X i ) .

i =1

Зададим произвольное вещественное число ε . В силу (29) существует K i такой, что

||x i_k — x i h < ^, V k>K i . r

Положим K = max Ki. Покажем, что Vk > K справедливо ||xk — x| < e. Зафиксируем 1 K. В силу (27) имеем

r hxk

—

x | =

— x

i =1

Используя (30), получаем

| x k — x | =

rr

2(^ ^{S ( x} k- 1 ⁾ — z i) — 2(^x i — z i )

i =1                        i =1

Сгруппировав, получим

^ X k - x | =

r

£ (^(x k— i ) - z i - X i + z i )

i =1

или, что то же самое

||xk - x | =

r

£(y s ^(x k - 1 ) ^{- x} i ) i =1

По лемме 1 отсюда следует

||xk - x | =

r

£(^x isk ^{- x} i ) i =1

Так как x ^k = n p i ( x ^k ) + z i и x i = n p i (x i ) + z i , то, подставляя указанные выражения в

(33),

получим

r

|| x k - x | =

£(ⁿ P i ^(x^ k ) ⁺ z i ^{- n} P i ^{( x} i ) ^- z i ) i =1

то есть

||xk - x | =

r

£(ⁿ P i ^{( x}^k ) ^{- n} P i ^{( x} i )) i =1

Замечаем, что в (34) под знаком суммы стоят взаимно ортогональные векторы. Квадрат нормы суммы ортогональных векторов равен сумме квадратов их норм. Поэтому из (34) следует

r

^{| x} k ^{- x | 2} = ^ || ⁿ P i ^{( x} i_S^k ) ^{- n} P i ( ^X i ) | • i =1

Это равносильно

,||2

^{| x} k ^{- x | 2} = ^ || ⁿ P i ^(x^ k ) ^{+ X} i ^{- n} P i ^{( x} i ) ^- z i ^ • i =1

Так как x^k = npi(x^k) + zi и xi = npi(xi) + zi, отсюда получаем r2

^{| x} k ^{- x | 2} = ^ | (^x i_s^k ^{- x} i ) | • i =1

С учетом (31), отсюда следует

| x k - x | ² <

^ (;тг) i =1

=r

(я

= E ² ,

то есть

|xk - x| < E, что и требовалось доказать.

Работа выполнена при поддержке гранта РФФИ № 09-01-00546а.