О силах, действующих на постоянный магнит, помещенный в прямоугольную полость с магнитной жидкостью

Задачи определения сил, действующих на тело, погруженное в магнитную жидкость, рассматриваются в литературе, начиная с классических работ Розенцвейга (см. [1]), в которых были выведены уравнение Бернулли для магнитной жидкости, магнитный скачок давления на границе намагничивающихся сред и общая формула, связывающая силу, действующую на немагнитное тело, с намагниченностью жидкости. Решение ряда конкретных проблем можно найти, например, в [2–5]. Интерес к этим задачам связан, в частности, с необходимостью теоретического обоснования работы магнитожидкостного сепаратора, разделяющего частицы цветных металлов по плотности, и магнитожидкостного акселерометра, в котором в качестве инерционной массы используется постоянный магнит или немагнитное тело, левитирующие в магнитной жидкости. Главной особенностью известных из литературы решений является то, что они получены в рамках приближения разбавленных растворов. В этом случае пренебрегают межчастичными (стерическими, магнитодипольными и гидродинамическими) взаимодействиями и игнорируют магнитное поле, создаваемое самой жидкостью (то есть размагничивающее поле). Кроме того, не принимают во внимание (но не всегда) магнитофорез коллоидных частиц (их дрейф под действием градиентного поля) и процессы диффузии. Все эти предположения накладывают серьезные ограничения на область применения полученных результатов. Так, согласно данным [6–8], межчастичные взаимодействия в концентрированных растворах могут увеличить намагниченность жидкости на десятки процентов, а размагничивающие поля могут привести к сильной дополнительной сегрегации частиц. Пренебрежение магнитофорезом и диффузией частиц означает, что известные решения справедливы только

на ограниченном промежутке времени, малом по сравнению со временем установления равновесного распределения частиц в полости.

Основная цель данной работы заключается в количественной оценке роли этих факторов на примере прямоугольной полости с магнитной жидкостью и постоянным магнитом. Выбранная геометрия расчетной области соответствует простейшему одноосному магнитожидкостному акселерометру, описанному в [1]. Задача решена численно в двумерной постановке.

Пусть имеется прямоугольная в плоскости { xz } полость размерами a 1 х Ь 1 , заполненная неподвижной магнитной жидкостью, в которую погружен постоянный магнит . Длина полости вдоль оси y полагается большой по сравнению с ее шириной a ₁ и высотой b ₁ . Магнит изготовлен из материала с большой коэрцитивной силой, поэтому его намагниченность M_s можно считать однородной и не зависящей от свойств жидкости, в которой он находится. Для определенности будем считать, что вектор намагниченности M направлен по оси x : M s = ( M s ,0,0 ) . Задача состоит в том, чтобы вычислить квазиупругую силу, действующую на магнит при его произвольном смещении по оси x относительно центра полости.

Поясним кратко появление квазиупругой силы. Магнитное поле H внутри жидкости складывается из поля H ₀ , создаваемого постоянным магнитом и убывающего с расстоянием от полюсов, и собственного поля h жидкости (то есть размагничивающего поля) H = H ₀ + h . Оба слагаемых в правой части последнего уравнения существенно неоднородны, поэтому неоднородна и магнитная добавка к статическому давлению p внутри жидкости. В соответствии с уравнением Бернулли для магнитной жидкости (см., например, [1]) эта добавка является монотонно возрастающей функцией напряженности H магнитного поля

H p = ц0 J MdH + const, (1) 0

где ц ₀ = 4 л- 10 - 7 Гн/м, M = M ( H ) — намагниченность жидкости. Из уравнения (1) следует, что любое немагнитное тело, помещенное в магнитную жидкость, будет выталкиваться ею в область с минимальной напряженностью магнитного поля. Под «немагнитным» телом здесь и далее понимается тело, намагниченность которого мала по сравнению с намагниченностью жидкости. Роль такого немагнитного тела могут играть в том числе и стенки полости, в которой находится магнитная жидкость.

Силу F , действующую на немагнитное тело, можно найти, проинтегрировав по поверхности тела силы давления (1) и приняв во внимание добавки, связанные с магнитным скачком давления на границе двух сред. Согласно [1] имеем:

F =J( p + Ц0 M2/2) dS, (2) s где Mn — нормальная компонента намагниченности.

При интегрировании по внутренней поверхности полости находим силу, действующую на стенки полости, а сила, действующая на магнит, получается из (2) простой сменой знака в правой части уравнения. Если магнит размещается в центре полости, распределение давления по ее внутренней поверхности симметричное, и результирующая сила, действующая на магнит, равняется нулю. Это положение магнита соответствует минимуму потенциальной (магнитостатической) энергии системы — магнит самоцентрируется. Смещение магнита из положения равновесия нарушает симметричность поля H и приводит к появлению квазиупругой силы.

Второй способ вычисления силы, действующей на магнит, подразумевает интегрирование по поверхности магнита, но в этом случае к правой части уравнения (2) необходимо добавить действующие на магнит объемные пондеромоторные силы, плотность которых составляет f = ц ₀ ( M s -V ) - H s , где H _s — вектор напряженности поля внутри магнита. Необходимость дополнительных вычислений этой напряженности делает второй способ более трудоемким. Кроме того, он менее точен при численном решении задачи, так как вблизи поверхности магнита наблюдаются самые большие градиенты напряженности и намагниченности жидкости. По этой причине в дальнейшем будем использовать формулу (2) с интегрированием по внутренней поверхности полости.

Несмотря на кажущуюся простоту формулы (2), ее применение связано с преодолением ряда серьезных вычислительных проблем. Главная проблема состоит в том, что входящая в формулу намагниченность сама является неизвестной функцией координат. Она зависит от напряженности поля H и объемной доли

Ф коллоидных частиц в жидкости, которые, в свою очередь, зависят от намагниченности. Это означает, вообще говоря, необходимость численного решения системы связанных уравнений, которая включает в себя уравнения Максвелла для напряженности и индукции магнитного поля (магнитостатическая задача), динамическое уравнение массообмена для магнитной жидкости, материальное уравнение, связывающее намагниченность жидкости с напряженностью поля и концентрацией частиц, уравнения, описывающие поле постоянного магнита.

3.    Поле постоянного магнита

Задача определения магнитного поля в окрестности однородно намагниченного магнита, имеющего форму прямоугольного параллелепипеда произвольных размеров, решена аналитически [9]. Для магнита, у которого длина вдоль оси y много больше его поперечных размеров, напряженность магнитного поля в произвольной точке P ( x , z ) определяется системой уравнений:

H х=- Ms Arc - M ig, 0x 2п       2п (rx + a 2/2)2 +(rz + b2/2)2 Lg = ln г           2             2n (rx + a 2/2) +(rz - b2/2) ,          rx + a, /2        rx - a, /2 Arc = arctg      2/ + arctg      2' rz + b2/2        rz -b2/2 Hz = -— Arc-— Lg , 0z 2n       2n (rx - a2/2)2 +(rz - b2/2)2 + In ------------2----------------4,                    (3) (rx - a2/2) +(rz + b2/2) rx - a, /2        rx + a, /2 arctg     , - arctg     ,     , rz + b2/2        rz - b2/2 где a2 , b2 — размеры магнита вдоль осей x и z соответственно; Msx , Msz — компоненты намагниченности постоянного магнита; rx = x - x0, rz = z - z0 — проекции радиус-вектора, проведенного из центра магнита в точку P(x, z). Как уже говорилось выше, в работе полагается Msx = Ms, Msz = 0 . В этом случае напряженность поля достигает максимальных значений на полюсах магнита x = x0 ± a2 /2. В частности, в среднем сечении магнита z = 0 напряженность на полюсах равняется

M     [ 2 a₂

,

H 0 z = 0.

H p = H 0 x = — ^arc tg | n      / b ₂

Это значение напряженности в центральной части полюсов магнита удобно выбрать в качестве основного параметра, характеризующего «внешнее» поле, действующее на магнитную жидкость, и поставить ему в соответствие безразмерный параметр Ланжевена ^ ₀ = ц ₀ mH_P ( kkT ) , который определяет характерную намагниченность жидкости вблизи полюсов. Здесь: m — магнитный момент коллоидной частицы; k — постоянная Больцмана; T — температура. Значение параметра Ланжевена вдали от полюсов (то есть безразмерное магнитное поле в произвольной точке, выраженное через локальную напряженность поля), будут заведомо меньше ^ ₀ и подлежит вычислению. На рисунке 1 в качестве примера приведены изолинии магнитного поля (параметра Ланжевена), создаваемого магнитом с отношением сторон 1:5 при ^ ₀=13 .

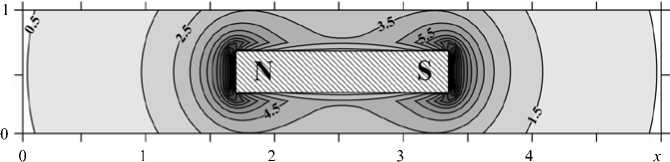
Рис. 1. Напряженность поля, создаваемого постоянным магнитом, расположенным в центре прямоугольной полости; £ 0 = 13

4.    Собственное поле магнитной жидкости

Напряженность поля внутри магнитной жидкости отличается от напряженности поля, созданного магнитом, в меру поля, создаваемого самой жидкостью, то есть размагничивающего поля. Размагничивающее поле вычисляется обычно путем решения сопряженной краевой задачи для некоторой геометрической области, включающей в себя собственно намагниченное тело (магнитную жидкость)

и окружающее пространство. Если в намагничивающейся среде нет электрических токов, то задача сводится к решению статических уравнений Максвелла и материального уравнения, связывающего векторы намагниченности M и напряженности H внутри вещества. На границе тела накладывается условие непрерывности нормальной компоненты магнитной индукции B = Ц о ( H + M ) и тангенциальных компонент напряженности. Однако при численном решении задачи возникает серьезная проблема, связанная с дальнодействующим характером магнитных полей. Границы внешней области должны быть настолько удалены от центра полости, чтобы обеспечивалось затухание магнитного поля, но достаточно близки, чтобы размер массива переменных оставался в разумных пределах и соответствовал возможностям компьютера. Вынужденный компромисс представляет собой источник некоторой трудно оцениваемой систематической погрешности.

Эта погрешность отсутствует при применении метода узкой щели, предложенного в [10]. Метод использует то обстоятельство, что в узкой щели, вырезанной в пробной элементарной ячейке и содержащей точку P ( x , z ), продольная компонента напряженности совпадает с продольной компонентой напряженности в самом теле, и такое же соотношение выполняется для поперечной компоненты индукции. Такая ситуация является прямым следствием граничных условий для индукции и напряженности магнитного поля. Согласно принципу суперпозиции вклад магнитной жидкости в напряженность H в точке P ( х , z ) определяется суммированием вкладов А Н всех элементарных ячеек, содержащих магнитную жидкость, но вклад пробной ячейки с точкой P ( х , z ) внутри вычисляется отдельно. Если размер элементарной ячейки достаточно мал и намагниченность внутри нее можно считать однородной, то для вычисления А Н можно использовать формулы, эквивалентные (3), в которых заменены размеры магнита на размеры элементарной ячейки ( А х и A z ), а rx и rz — на проекции радиус-вектора, соединяющего центр элементарной ячейки ( х 0 , z 0 ) с точкой P ( х , z ) , на координатные оси. Просуммировав вклады А Н всех внешних (по отношению к точке P ) элементарных ячеек, прибавляя к этой сумме вклад пробной ячейки и напряженность поля магнита, получим выражения для компонент напряженности поля в магнитной жидкости:

H_x ( х , z ) = H 0 x ( х , z ) + £ A H_x - 2 M_x ( х , z ) arctan x * x o

H_z ( x , z ) = H 0 _z ( x , z ) + £ A H_z -П M_z ( x , z ) arctan ^z * ^z 0

Добавки к внешнему полю в правой части уравнения (4) и есть размагничивающее поле, то есть поле, создаваемое самой магнитной жидкостью. Если намагниченность среды M ( х , z ) как функция координат известна, то формулы (3), (4) однозначно определяют напряженность магнитного поля как внутри, так и снаружи жидкости.

В случае разбавленных растворов эффекты, связанные с магнитодипольными межчастичными взаимодействиями, играют второстепенную роль, и ими можно пренебречь. Для учета межчастичных взаимодействий в концентрированной жидкости ее намагниченность M , входящая в правую часть уравнений (4), вычислялась в рамках модифицированной модели эффективного поля второго порядка, справедливой в достаточно широком диапазоне параметров [11]:

M = mnL  )Н, ^=^0^, eH ekT

MH

H = H + L^ ’ e 3

1+± ^dM-H ) 48 dH

M L = mnL ( £ ) ,

где n = б фДп d ³)

числовая плотность частиц; d — диаметр частицы с защитной оболочкой;

L(^) = cth(^) - V^ — функция Ланжевена; ML — намагниченность жидкости, вычисленная в рамках ланжевеновского приближения; He — эффективное поле, действующее на частицу. Уравнения (5) многократно проверялись различными методами. Они хорошо описывают экспериментальные данные по начальной восприимчивости магнитных жидкостей и результаты численного моделирования в области малых и умеренных значений энергии магнитодипольных взаимодействий [6, 7, 12]. При решении динамического уравнения массопереноса в магнитной жидкости (см. следующий раздел) шаг по времени сопровождался уточнением магнитного поля и намагниченности путем последовательного применения уравнений (3)–(5) к каждой элементарной ячейке. При этом использовался двухшаговый итерационный алгоритм, обеспечивающий лучшую сходимость по сравнению с пошаговым алгоритмом.

5.    Магнитофорез и диффузия частиц в концентрированных магнитных жидкостях

Под действием магнитного поля первоначально однородная магнитная жидкость со временем становится пространственно неоднородной по концентрации магнитной фазы вследствие магнитофореза частиц (движения частиц под действием неоднородного магнитного поля). В отсутствие конвективного движения единственным фактором, препятствующим этому расслоению, является градиентная диффузия. В концентрированных системах эти процессы описываются нелинейным динамическим уравнением массообмена, содержащим слагаемое, ответственное за магнитофорез и зависящее от намагниченности и напряженности поля в веществе. Последнее обстоятельство особенно важно. Оно означает, что магнитная и диффузионная части задачи должны решаться совместно. Главная особенность диффузионных процессов в магнитной жидкости состоит в том, что характерное время затухания концентрационных возмущений т D « LJ ( п ² D ) минимум на шесть-семь порядков превышает время релаксации магнитного момента т B ® 3 п V(kkT ) ( L — характерный размер полости, D — коэффициент диффузии, п — вязкость магнитной жидкости, V — объем коллоидной частицы). По этой причине намагниченность жидкости можно считать термодинамически равновесной с очень хорошей степенью точности, а на этапе вычисления магнитного поля концентрационное поле рассматривать как замороженное.

Различные варианты уравнения массообмена, отличающиеся полнотой учета межчастичных взаимодействий и анизотропии коэффициентов переноса, предлагались ранее в [13–20]. В данной работе используется уравнение из [20], которое описывает изменение объемной доли коллоидных частиц ф в пространстве и во времени при отсутствии конвективных течений:

Дот                       , ,         , lT = -dv Ьо K (ф)кL (^, )V(^,)- 1 + dt               I I

2 ф ( 4 -ф ) д ² ( ф ² G ) ( 1 -ф ) ⁴ -^Ф дф ²

Vф^ ,

G ( X , ф ) = 3 X ²

( 1 + 0,04 X 2 ) ( 1 + 1,28972 ф + 0,72543 ф ² ) ( 1 + 0,308 X ² ф )       ( 1 + 0,83333 Хф )

Здесь: K(ф) = b]b0 (b и b0 — подвижности частиц в магнитной жидкости и жидкости-носителе, соответственно); D0 = b0kT — эйнштейновское значение

коэффициента диффузии; X = ц ₀ m ² Д4 п d³kT ) —

параметр магнитодипольных взаимодействий (отношение энергии диполь-дипольных взаимодействий при контакте двух частиц к энергии теплового движения); G(X, ф) — относительный вклад магнитодипольных взаимодействий в плотность свободной энергии. Первое слагаемое в (6) отвечает за магнитофорез, второе — за диффузию, третье — за стерические взаимодействия и последнее — за эффективное притяжение частиц, связанное с магнитодипольными взаимодействиями. Эффективный параметр Ланжевена ^e, определяющий интенсивность магнитофореза, задается уравнением (5). В правой части (6) коэффициент при Vф в фигурных скобках можно рассматривать как изотропную часть коэффициента диффузии D коллоидных частиц, зависящую от их объемной концентрации и энергии магнитодипольных взаимодействий:

D = D 0 K ( ф )

1 +

2 ф ( 4 -ф ) д ² ( ф ² G ) ( 1 -ф ) 4 ^ф дф ²

Аппроксимация (7) для свободной энергии обеспечивает хорошее количественное согласие с результатами численных расчетов при X <  2 . Система уравнений (6), (7) хорошо описывает также результаты численных экспериментов по сегрегации частиц в области X <  2 и ф <  0,4. При X >  3 это количественное согласие нарушается, однако фазовая диаграмма для спинодального распада системы, полученная на основе уравнения (7), выглядит вполне реалистично. В частности, критическое значение параметра X , соответствующее спинодальному распаду, находится в интервале значений, определенных другими методами [20].

6.    Метод решения и результаты

Связанная система уравнений (4)–(7) решалась численно, методом конечных объемов, в двумерной постановке по явной схеме. Система координат соответствовала рисунку 1. Влияние гравитационного поля не учитывалось. Уравнение магнитодиффузии было приведено к безразмерному виду. В качестве единицы длины была выбрана высота прямоугольной полости b1 , а единицей измерения времени служило время затухания концентрационных возмущений в разбавленном растворе т = b12 /D0 . Координаты узлов расчетной сетки располагались в центрах прямоугольных элементарных ячеек. Такой подход упростил расчетную схему и позволил избавиться от проблем, связанных с расходимостью магнитного поля на ребрах постоянного магнита. Устойчивость решения обеспечивалась выбором шага At по времени. Этот шаг изменялся в процессе счета в зависимости от максимального значения эффективного коэффициента диффузии D в полости, определяемого формулой (8), который, в свою очередь, зависел от локальной концентрации частиц. В безразмерной форме шаг по времени составлял At = 0,45(1/Ax2 +1)Az2) Jdmax. Концентрационная зависимость относительной подвижности частиц аппроксимировалась формулой Рассела [21] K(ф) = (1 - ф)6,5.

Так как границы полости и постоянного магнита непроницаемы для вещества, нормальная компонента полного потока частиц на границе равняется нулю. Это условие легко выполняется при численной реализации метода конечных объемов: вводится дополнительный слой элементарных ячеек, примыкающий к границам полости снаружи. В этих — буферных, ячейках концентрация частиц и напряженность эффективного поля приравниваются к соответствующим величинам в пограничных ячейках внутри полости, что автоматически «зануляет» поток частиц через границу. Прием имеет тот недостаток, что он не пригоден для внутренних границ с плавающим в жидкости твердым телом, что имеет место в данной работе. Поэтому здесь применялся другой вариант, в котором для пограничных ячеек записывалось отдельное условие баланса частиц, изначально исключающее локальный поток через границу полости.

В качестве начального условия использовалось однородное распределение частиц, наблюдаемое в реальных условиях сразу после заполнения полости. Равновесное неоднородное распределение частиц в полости устанавливалось через некоторое время в диапазоне от 5 до 50 безразмерных единиц в зависимости от значений параметра магнитодипольных взаимодействий и положения магнита в полости. Для вычисления x -компоненты силы, действующей на магнит, в качестве поверхности интегрирования в (2) выбирались боковые поверхности полости. Как следует из (1), (2), элементарное приращение силы, соответствующее одному шагу A z по вертикальной координате, составляет

Ф2j L(^)d^ — Ф1 j L(^)d^ Azz , где индекс 1 относится к левой границе полости, а 2 — к правой. Формула записана в безразмерном виде. За единицу измерения давления принята величина 6kT/(лd3), сопоставимая с максимально возможным осмотическим давлением коллоидных частиц в отсутствие магнитного поля.

Основными безразмерными параметрами, определяющими интенсивность магнитофореза и структуру концентрационных полей в полости, выступали: средняя по объему концентрация ^; параметр Ланжевена с ₀, определенный через магнитное поле на торцах магнита; параметр магнитодипольных взаимодействий X . Большинство представленных ниже результатов получено для средней по объему концентрации частиц (ф) = 0,1 и безразмерного поля (параметра Ланжевена) на торцах магнита ( с ₀ = 13), типичных для реальных систем. Для более наглядной демонстрации эффектов, связанных с магнитодипольными межчастичными взаимодействиями полагалось, что X = 2, хотя для коммерческих магнитных жидкостей обычно X <  1. Отметим, что увеличение параметра X в два раза вполне достижимо в реальных жидкостях [6, 24], а применительно к частицам из магнетита соответствует относительно небольшому увеличению среднего диаметра частиц на 20–30%.

Процесс решения системы уравнений по времени продолжался до тех пор, пока не достигалось стационарное состояние. Динамика процесса подробно не исследовалась, так как рассматриваемая здесь система имеет несколько характерных размеров (это — ширина и высота полости, размеры зазоров между магнитом и стенками полости), каждому из которых соответствует свое диффузионное время. Кроме того, свое характерное время добавляет скорость магнитофореза. Анализ динамики в таких условиях становится чрезвычайно громоздким и выходит за рамки данной работы.

Задача решена в трех вариантах.

Вариант 1. Постановка простейшая, то есть не учитываются межчастичные взаимодействия и размагничивающие поля (приближение разбавленных растворов), а также магнитофорез. В этом случае намагниченность жидкости однозначно связана с полем постоянного магнита, задаваемым формулой (3)

H        ^0 mH

M = mnL ( £)— ,     ^ = —:---

H        kT

Проблемы, которые могли быть обусловлены неоднородностью концентрационного и существованием размагничивающего полей, отсутствуют. Числовая концентрация частиц n и соответствующая ей объемная доля ф полагаются однородными по всему объему полости. Магнитостатическое давление и сила, действующая на магнит, находятся простой подстановкой (9) в уравнения (1) и (2).

Вариант 2. Решение получено в приближении разбавленных растворов, но с учетом магнитофореза и диффузии частиц. Концентрация частиц неоднородна и подлежит определению. К уравнению (9) добавляется уравнение массопереноса, получающееся из (6) после удаления слагаемых, ответственных за межчастичные (стерические, магнитодипольные и гидродинамические) взаимодействия дф/3 t = - D 0 div [ф L ( £ ) V£-Уф] . В стационарном случае последнее уравнение имеет общее решение вида [22]

, V    sh ( ^ )

ф = (ф) V

, sh U)

J 4s2 dV

V ^

Для одномерного случая уравнение, аналогичное (10), получено ранее в [23].

Вариант 3. Постановка максимально полная, то есть учитываются магнитофорез, диффузия, размагничивающие поля и межчастичные взаимодействия. Решалась система уравнений ( 1)–(3), (5)–(7).

Результаты расчетов приведены на рисунках 2–5. На рисунке 2, а показаны изолинии равной концентрации при центральном положении магнита в полости. Рисунок демонстрирует роль магнитофореза в пространственном перераспределении частиц. Видно, что эффект очень сильный: концентрация коллоидных частиц вблизи полюсов магнита примерно в три раза превышает концентрацию на периферии. Ясно, что такими сильными эффектами пренебрегать нельзя.

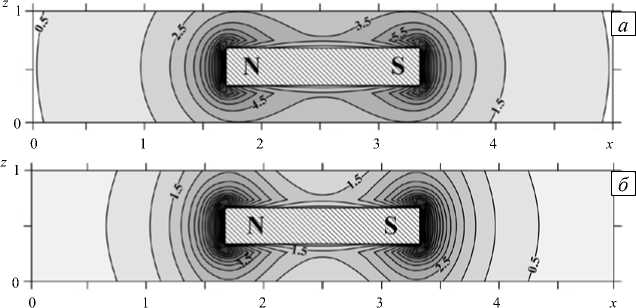
Рис. 2. Изолинии равной концентрации частиц ( а ) и размагничивающего поля в терминах параметра Ланжевена ( б ) в прямоугольной полости при центральном положении магнита для варианта полной постановки при (ф} = 0,1 , ^ 0 = 13 , X = 2

Рисунок 2, б содержит изолинии размагничивающего поля, созданного магнитной жидкостью в поперечном сечении цилиндра. Размагничивающее поле представлено в безразмерном виде — как параметр Ланжевена, определенный через модуль напряженности. При выбранных входных данных оно имеет такие же по порядку величины значения, как и поле постоянного магнита. Структура размагничивающего поля также напоминает структуру поля постоянного магнита (см. Рис. 1). Так как эти поля преимущественно направлены навстречу друг другу, суммарное поле может оказаться в несколько раз меньше поля магнита. Это обстоятельство означает многократное уменьшение квазиупругой силы, действующей на магнит. Слой магнитной жидкости с повышенной концентрацией частиц, примыкающий к торцам магнита, эффективно экранирует его поле. Эффект усиливается с ростом параметра магнитодипольных взаимодействий.

Влияние магнитофореза на квазиупругую силу, возникающую при смещении магнита из центрального положения, продемонстрировано на рисунке 3. Кривые 1 – 3 соответствуют трем вариантам решения задачи, перечисленным выше. По оси ординат отложена x -компонента силы, взятая по модулю. Видно, что решение задачи в приближении разбавленных растворов без учета магнитофореза (кривая 1 ) предсказывает многократно завышенное значение силы. Учет магнитофореза приводит к уменьшению квазиупругой силы примерно на порядок (кривая 2 ). Основная причина этого эффекта — экранирование постоянного магнита слоем высококонцентрированной жидкости, образующимся вблизи полюсов, и, как следствие, уменьшение концентрации частиц на границах полости. Результатом магнитофореза является многократное уменьшение намагниченности жидкости и магнитного давления на границах полости. Отметим, что именно в таком приближении ранее решена задача о силах, действующих на левитирующее в магнитной жидкости немагнитное тело [23]. Наконец, кривая 3 демонстрирует суммарный эффект, связанный с межчастичными взаимодействиями и размагничивающими полями. Это влияние разнонаправленное. Стерические взаимодействия (эффекты исключенного объема) препятствуют сегрегации частиц [20] и тем самым увеличивают расчетное значение квазиупругой силы. Магнитодипольные взаимодействия, напротив, усиливают сегрегацию частиц (квазиупругая сила

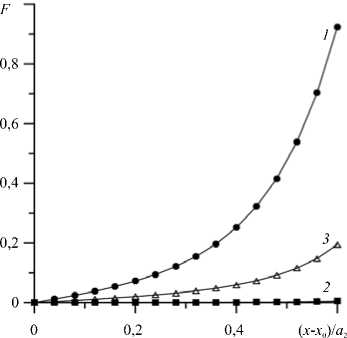
Рис. 3. Квазиупругая сила, действующая на магнит, в зависимости от его смещения из центрального положения; (ф) = 0,1, ^ q = 13, X = 2; номера кривых соответствуют трем вариантам решения задачи

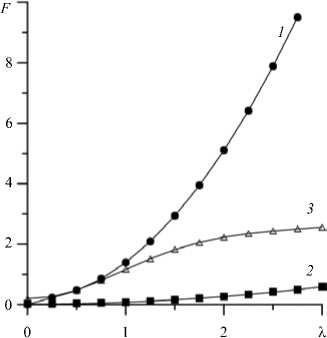
Рис. 4. Квазиупругая сила, действующая на магнит, в зависимости от параметра магнитодипольных взаимодействий при фиксированном смещении магнита 0,84; (ф> 0,1, ^ = 13

на равновесную намагниченность в области

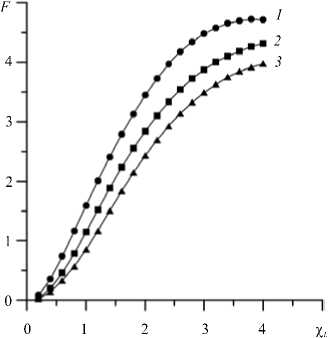
Рис. 5. Квазиупругая сила, действующая на магнит, в зависимости от ланжевеновской восприимчивости исходной жидкости при относительном смещении магнита 0,84 и £ q = 13 . Кривая 1 соответствует X = 1;

уменьшается), но, кроме того, увеличивают намагниченность жидкости (сила растет). Размагничивающее поле ослабляет квазиупругую силу во всех случаях.

Наконец, на рисунке 4 приведена зависимость квазиупругой силы от параметра магнитодипольных взаимодействий при фиксированном относительном смещении магнита, равном 0,84, и средней концентрации частиц (ф) = 0,1. Разница между кривыми 1 и 2 (номера кривых соответствуют трем вариантам решения задачи) обусловлена влиянием магнитофореза, а разница между кривыми 2 и 3 — влиянием межчастичных взаимодействий и размагничивающего поля. Воздействие этих факторов очень сильное, а пренебрежение ими может привести к систематической ошибке в сотни процентов. Кроме того, у кривой 3 видна тенденция к насыщению, вызванная межчастичными взаимодействиями, а у кривых 1 и 2 эта тенденция, естественно, не наблюдается. С учетом сказанного выше результаты на рисунке 4 вполне предсказуемы: с ростом X увеличивается намагниченность жидкости и, соответственно, квазиупругая сила.

В этой связи напомним, что универсальной мерой влияния межчастичных взаимодействий слабых магнитных полей служит ланжевеновская восприимчивость х L = Ц ₀ m 2 ( ^й )/(3 kT ) = 8X^ [25]. Начальная восприимчивость жидкости зависит только от произведения X и ф , то есть от х L в широком диапазоне безразмерных параметров. Квазиупругая сила, действующая на левитирующий магнит, этому правилу, строго говоря, не починяется, так как в уравнения (6), (7), параметры X и ф входят по отдельности. Тем не менее, величина х L остается главным безразмерным параметром, определяющим силу    F . Семейство кривых    F = F ( х L , (ф) )

демонстрирует существенно меньший разброс по сравнению с семейством F = F ( X , (ф) ) . В качестве примера на рисунке 5 приведены зависимости квазиупругой силы от средней концентрации частиц (ф^ при фиксированных значениях X , но кривые построены в координатах ( х L , F ). Видно, что при фиксированном значении х L изменение X в 2,5 раза приводит к изменению силы только на 20–30%.

2 - X = 2; 3 - X = 2,5 . Задача в полной постановке

7.    Заключение

Итак, численно решена задача определения сил, действующих на постоянный магнит, помещенный в прямоугольную полость с магнитной жидкостью. Задача реализована в двумерной постановке с учетом магнитофореза и диффузии частиц, размагничивающих полей и межчастичных взаимодействий. Рассчитаны размагничивающее поле и поле концентрации коллоидных частиц. Приведена зависимость результирующей силы, действующей на магнит, от его смещения из положения равновесия, параметра агрегирования и концентрации частиц. Основной итог работы — демонстрация очень сильной зависимости результатов расчета от выбора теоретической модели. Показано, в частности, что пренебрежение межчастичными взаимодействиями в жидкости может привести к погрешности в расчетных данных в сотни процентов.

Разумеется, взятое за основу уравнение массопереноса в магнитной жидкости (6) само является приближенным, так как при его выводе использовался целый ряд серьезных допущений, включая экстраполирование формулы (7) для свободной энергии на область сильных магнитных полей, где ее применимость неочевидна [20]. Тем не менее, не следует ожидать большой погрешности в результатах расчета, вызванной этой экстраполяцией, так как относительный вклад магнитодипольных взаимодействий в свойства системы быстро уменьшается по мере усиления внешнего поля. Исключение составляют только результаты, полученные при больших параметрах агрегирования ( X >  2), при которых возможен фазовый переход типа «газ – жидкость». Хотя в данной работе такие переходы не наблюдались, к результатам в области X >  2 следует относиться с некоторой осторожностью. Отсутствие в настоящее время достаточно точных аппроксимаций для относительной подвижности частиц при их большой концентрации потенциально может привести к существенным погрешностям в динамических свойствах системы, но не способно повлиять на описание стационарных состояний, исследуемых в данной работе.

Работа выполнена при поддержке РФФИ (проект № 13-02-00076-а) и Уральского отделения РАН (проект № 12-T-1-1008).