О системе дифференциальных уравнений, описывающей отображения, близкие к растяжению

TTiin... Ln... тппп dx1 Л ... Л dxn.

Обозначив в последнем равенстве через detMT(L,i) - детерминант матрицы Мт со столбцом коэффициентов L^...,!^ вместо г-го столбца, получаем dAl = (—1)г(п — l)detMr(L, i^dx1 Л ... Л dxn.

Отсюда *_ndA’ = (—1)^г(п - l)detM^T(L,i) и тогда detM^T(L,i) = ⁽       •

Рассматривая далее систему линейных уравнений M^Tb = (Ly,..., L_n')^T с неизвестным вектор-столбцом Ь, согласно формуле Крамера и последнему равенству, имеем: by =                                     ⁼ 1,---,тг). Заметим, что

1         detMJ         detM n-1                      '             ’ detM = det (/'/ (^tr/')) = det/'/ (^tr/')n / 0 всюду в D по условию теоремы.

Следовательно, в каждой точке х 6 D имеем:

M^Tb = (L_b..., L^^T и Lj = 52™ i ^тч^Ьг (7 = 7 n-Y Отсюда

71                 П П

L = Ljdx^j = УУУ2 ^ijbydx³ = j=l           ;=1 i=l

7Z 71                                 71                           71 -| / -. \ ^ i * 2

= lAE™»^ = Еь-М‘ = Е^й-Зт-^ =KwY г=1 j="l              i=l            г=1

Итак, L(x) = dln\T(xY = K^M^Y Теорема доказана.

Формула (3) выражает основное необходимое условие существования решений системы (2). Пользуясь соотношением (3), получим еще несколько необходимых условий существования решений системы (2), которым удовлетворяет матрица м(х') = f^/vY^f'^Y

Следствие 1. При выполнении условий теоремы 1 справедливы равенства:

dK(M) = 0,(4)

dM1 = М1 ^^(M') (г = 1,...,п),(5)

dM{ ^ М3 + М{ Л dM3 = 0 (г, у = 1,...,п).(6)

Доказательство. Последовательно получим указанные равенства:

• а)    дЦМ) = dVdln\T\) = 0;

• б)    dM¹ = d^ = V-Wdf ^ dT'¹ = ^ Л f = Л^ Л din \T\ = M^l Л ЦМУ

• в)    dM¹ Л М³ + Mⁱ Л dM³ =) М^г Л Л М³ + М^г Л М³ Л Л =

= -М¹ Л М³ Л Л + МЧМ³ Л Л = 0.

Следствие доказано.

Взаимосвязь равенств, полученных в следствии 1, показывают следующие утвер ждения.

Следствие 2. Пусть D — область 6 ^(п > 3) и М(ж) 6 C‘²(D) — матрица размерности п х п с detM(x) ^ 0, trM(x) = п, х Е D. Равенства (6): дМ^г Л М³ + М¹ Л dM³ = 0 (i,j= 1, ...,п) выполняются тогда и только тогда, когда справедливы соотношения (5): dM^-1 = М^г Л Л(М) (г = 1, ....п).

Доказательство. Рассмотрим следующие вспомогательные (п — 2)-формы

= (-iySgn(i-

Покажем, что из условий (6) и определения формы Л(М) вытекают формулы:

dM4 ^ = dM³ Л ^^З’^р\                 (7)

dA1 =-(п-1)Л(М) Л Аг,                      (8)

'М,Р =       г,з ^р.

Докажем соотношение (7). Зафиксируем натуральные числа i,j, г < j. Выберем Р Е N, р г,з.

Рассмотрим случай г < у <  р. Тогда

Д(чл) =

= ^vyYMY м.Л "..мму и пользуясь (6), имеем dM1 л д^-р) = (-iy-1dMi ^MY Л ...v... Л М3 Л Л Мп =

= (-ly^'^dM1 ^M3                 =

= (My⁺³dM³ Л М^г Л M^Y Л ..Л - v..^Mⁿ =

= (-^^НзШг”^х^М³ Л М¹ Л ... Л М^г Л ..Л М^п = dM³ Л ^^З’^р\

Пусть г < р < j. Тогда

Д(ЧР) = ^-iy-41A Л v V А мп, дЬ'.р) = (-тум1 Л ..." V... д МТ\ и из (6) получаем dM1 Л Д^’р^ = (-1У"^Мг Л М1 Л ...V V... Л М3 Л ... Л мп =

= (-ly+WATPAM^.-v v v...A,Mⁿ =

= (-l)^i+HdMMMⁱAM¹A.J v У.^М^п =

= (—iydM^j Л М¹ Л ..." V... л М^п = dM³ А

Наконец, пусть р < г < j. Тогда

На основании (6) имеем:

dM¹ л д^ = (-lydM¹ л м¹ лv vл м^' лл м^п =

= (-ly^dM¹ Л М³ AM¹ Л..." ’L.AAf =

= (-iy+jdMj ^мг ^м1 л..Л t L.Mvr =

= (-iydM3 ^M1           = dM3 ^’p\

Итак, формулы (7) доказаны.

Проверим справедливость равенств (8). В самом деле,

-(п - 1)Л(М)=

= -(п- У ^^-М3 Л *ndkh Л Д' = v AdeW^n-l

• -    -(-!)' *n Wy-Vf'M1 Л Л Мп-^-(9)

Так как М^т Л ... Л М^п = detMds¹ Л ... Л dx¹\ последнее выражение в (9) равно

*п(й?Д’)с/х1 Л Л dx11 = ^Д1, и мы приходим к соотношению (8).

В теории полилинейных форм хорошо известно следующее утверждение [4]: Пусть Q — некоторая полилинейная кососимметрическая форма над Rⁿ степени к и а есть 1-форма. Для того чтобы форма Q допускала представление

П = ш Л а, где ш — некоторая (к — 1)-форма, необходимо и достаточно выполнения равенства Q Л а = 0. В силу условий dM1 Л Мг = 0, г = 1,...,п, вытекающих из (6), и сформулированного выше утверждения справедливы равенства dM' = M'AA' (г = 1,...,п).                     (10)

Здесь А^г — некоторые 1-формы. Дифференциальные формы Л4¹,...,М^п образуют базис пространства 1-форм в каждой точке х Е D. Поэтому найдутся такие функции Aj — коэффициенты форм А^г относительно базиса М\ г = 1,...,п, что

А = ^АХМУ

Условиями (10) формы А^г не определяются однозначно. Например, из (10) видно, что значение коэффициента А¹- может быть произвольным. Поэтому условимся считать, что А- — Aj, где Л₁₅ ...,Л_Т1 — коэффициенты разложения дифференциальной формы Л(М) по базису М\...,М^п, т. е.

= Аг =

1 (-1)^г det М п — 1

АР Л ^Д'.

Покажем, что в этом случае А1 = ... = Ап = А(Му Заметим, что выполнение равенств (7) означает, что а; = а;(п)

для всех г, j,p = l,...,n, i,j р р. Докажем соотношения (11).

Выберем i,p € N, г > р. Тогда sgrpi — р) = 1 и справедливы равенства dAT л д(1’р) = Mi л Аг n ^ = а;м‘ л ар л д(г'А =

• -    -А^АР Л АР Л ... V... Л Мп = ИУА^М1 Л ... Л Мп.(12)

Пусть теперь г < р. Тогда sgn(i — р) — — 1 и dAP Л Д^А = АГ Л Аг Л Д(г'А = АрМг Л Мр Л =

• -    МГ'М^ЛГ Л АР Л АР л ... V V ... Л АГ =

= PAyApArA.-AAP.(13)

Равенства (7), (12), (13) доказывают справедливость соотношений (11).

Полагаем далее ар = Агр, г = 1,..., п, г р р.(14)

Отметим следующую формулу для вычисления внешнего дифференциала от внешнего произведения ш¹ Л ... Ад" т гладких 1-форм, заданных в D:

d(iP А Л шт) = ^(-l)^1^' А Л v... Л шт.(15)

2=1

Формула (15) легко доказывается по индукции и представляет собой следствие известного правила вычисления внешнего дифференциала от внешнего произведения двух гладких форм произвольных степеней [5]:

d(a Л Д) = da Л 3 + И^^е9аа Л d3-

Рассмотрим (п — 1)-форму

^г = М1 Л...Р.^А1п и, пользуясь (15), вычислим ее внешний дифференциал. Определим формы ш1, полагая а)1 = М1 при I = 1,..., г — 1 и ш1 = Ml+1 при I = г,..., n—1. Тогда Дг = и на основании (15) имеем

6?Д‘ = У^(-1)^г~Чи^г Л о? Л ...v Л ш^п~^т = z=i

= ^( —l)'^-1^' Аш¹ ^ ...V... Лу^,н| 4- ^(—1У^-1с?й? Auz¹ Л ...v... Aw^n-1 =

= ]Гм УЛ/ЛД Л М¹ Л V 0Л М^п + ^P(-VpdM^w А М¹ Л V ТЛ м^п.

Z=1

Отсюда, в силу определения форм Д(г-^, получаем d^ = ^dMl А ^ V^dMw Л Д(т-^ 1=11=г и, пользуясь установленными ранее соотношениями (12), (13), (14), из которых dMl^Д^^ = (—lya^M1 Л ... Л Мп, приходим к выражению dA* = Н№-1)сцМ1 А...АМп.(16)

Но из (8) следует, что

^Д¹ = (~1)^г(п - ПЛ.М¹ Л ... Л МА

Сравнивая последнюю'формулу с (16), заключаем, что А^ = а3 = Aj, г, j = l,.... п, г Д ]. Кроме того, ранее мы условились считать выполненными равенства А33 = К3. Значит, Aj = Kj, i,j = 1,...,п. Эти равенства означают, что А1 = ... = Ап = К(М) и, следовательно, dM' = Мг АЦМ\ г = 1,...;п.

Таким образом доказано, что из условий (6) вытекают соотношения (5).

Докажем теперь обратное, т. е., что при выполнении условий (5) следует выполнение соотношений (6). Действительно, dM1 Л Мг = Мг ^ Л(М) Л Mj

= -М^г Л М³ Л Л(М) = -М¹ Л dM³.

Следствие доказано.

Следствие 3. Пусть D — область в Rⁿ (п > 3) и М^ Е C²(D) — матрица размерности пхп с detMX ^ О, НМ^ = п, х Е D. Если выполняются равенства dM^l = М^г Л Л(М) (г = 1,..., п), то справедливо соотношение dAX) = О.

Доказательство. Установим следующие вспомогательные равенства d^M1 A...V VЛ м^ = -(п - 2)Л(М) Л(МТ Л ...v               (17)

Будем считать, что г < j. Определим формы ш¹, полагая ш¹ = М¹ при I = 1,..., г — 1, М = M^z+1 при I = г, ...,j — 1 и и? = М^т при I = j, ...,п — 2. Отметим, что

M^-v л,.ЛАГ = ^Л...лУ²

и, в силу (5), dM — и1 Л Л(М), I — 1,..., п — 2. Пользуясь формулой (15), имеем dX1 Л .М ЛМП) = п-2

= ^(-l)'"1^ Аш1 Л ...VЛ^п""2 =

Z=1

п— 2

= ^(-1)'" V л MX) Л ш¹ Л ... V ... л х'^ =

Z=1

п-2

= ~ ^Л(М) Л Л ... Л zZ~² = -М - 2)Л(М) Л М^х Л ... v V ... л М^п, Z=1

что и доказывает (17).

Из равенств (17), а также из (15) и К(М) Л dlVF ^ Л(М) Л (Мг Л Л(Л7)) = О, заключаем, что a^d(dxy a...v '...ллп) = -(п-Хм^м1 л..М М.г\Мп. (18)

Пусть dkX^ = ^is Л M^l — разложение для dMX) по базису M^s ^ М¹, 1 <  s < I < п . На основании формулы (18) получаем

О = дЦМ) Л М¹ Л ... v v... д М^п = 8.;_рМ^г /\ М^{Р Л} М^{1          мп} =

• . = ЗМ-Х^М¹ Л ... Л М^п = ЗМХ^-^еШдх¹ Л ... A dxⁿ.

• 2. Теорема существования

Значит, З-ij = 0 для всех г, у. 1<г<у<пи dKX) — 0.

Следствие доказано.

Следующая теорема показывает, что найденные необходимые условия существования решений системы ^х^^^-Мфф являются также и достаточными.

Теорема 2. Пусть D — односвязная область в Rⁿ (п >  3). Тогда, если матрица Мфф Е C^^D^-^ размерности п х п с detM^x) Д 0, 1гМ(ж) = п, х Е D такова, что dAT = АГ Л Л(М), то существует, и притом единственное, отображение f:D^Rⁿ класса C³(D), удовлетворяющее уравнению (2) и условиям нормировки:

КА = А

tr./»

п

где а — фиксированная точка из D, А Е R", г Е R¹. При этом отображение /(ж) выражается формулой

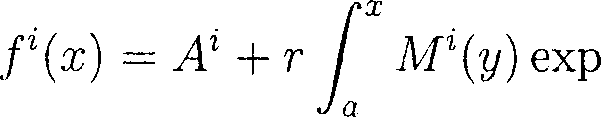
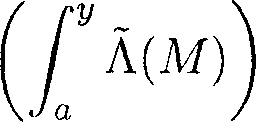
(г = 1,..., п).

Доказательство. Заметим сразу, что, согласно следствию 3, имеем dA = 0.

Рассмотрим функцию Ефф = exp(f^ Л(М)); здесь интегрирование ведется по гладкой кривой, лежащей в D, с началом в точке а и концом в точке у. Так как dA = 0, то интеграл в определении функции Е(у) зависит только от а и у.

Дифференциальные формы АГЕ, как и Л, замкнуты. Действительно, d(AFE) = dAT F + (-l)W Л dF = АР Л Л F - АГ А Л F = 0.

Следовательно, интеграл в определении функции РЮ -АЧт ]‘ф АГ (у) F (у) зависит только от а и х. Тогда имеем df^x) = тЕффАРфс), т. е. f' = rFM, откуда tr/' = г FAM = nrF и F = ^tr/', а значит, f^f = г Ют f'AI = А1ЮР (т. е. указанная в условии теоремы 1 функция / — действительно есть решение уравнения (2)). Кроме того, эта функция удовлетворяет условиям нормировки: РфГ) = А¹ + т ]ф АГ(у) ехр(фф Л(М)) = А¹, г — 1, ...,п (т. е. /(а) = Д); и так как dF = г FAR, то - HfAad — - rF НА1\ = тЕЮ = т.

Докажем теперь единственность этого решения. Пусть ф: D —» RT — еще одно решение уравнения (2), удовлетворяющее указанным условиям нормировки. Положим ТуА) = ^tr/^z(x) = тЕфф = г exp J^ А (откуда Т] Д 0), Тзфф = Цтф'(х\

Так как рассматриваем Д ip Е C^yD^ — решения уравнения (2), то для них с необходимостью выполнены (см. теорему 1) условия:

^ = jln|Tt| = A(<; = l,2).

1k

Отсюда dT_k = ХТ_к (к = 1,2). Поэтому имеем (учитывая IX ^ 0):

,.Т2.  d^-^dT, МТ2ТА-Т2Тф и значит Т2(х)=сТ1(тф, где с - некоторая постоянная. А поскольку Тл\а^=Т2^а^~ т\ то с = 1 и Т2фхф — Т^х\

Итак, -ф'^х) = М(х)Т₂(х) = М^Т^х) = Г(хф Отсюда и из -ффф = f(a) = А следует равенство: ^(ж) = /(я), ж Е D.

Теорема доказана.

ON A SYSTEM OF DIFFERENTIAL EQUATIONS DESCRIBING MAPPINGS ARE CLOSED TO DILATATION

The system of the differential equations with partial derivatives, describing the smooth mappings close to dilatation is considered. Results of search of integrability this system in space of smooth functions are stated.

• 1.    Решетник Ю.Г. Пространственные отображения с ограниченным искажением. Новосибирск: Наука, 1982.       '

• 2.    Гольдштейн В.М., Решетняк Ю.Г. Введение в теорию функций с обобщенными производными и квазиконформные отображения. М.: Наука, 1983.

• 3.    Журавлев И.В. Вопросы существования в теории пространственных отображений с ограниченным искажением: Дис. ... д-ра физ.-мат. наук (на правах рукописи). 1993.

• 4.    Slebodziiiski W. Exterior forms and their applications. Warszawa: PWN, 1970.

• 5.    Зорич В.А. Математический анализ. M.: МЦНМО, 1998. Ч. II.