О следах - операторов, сосредоточенных на подмногообразиях

Для пары ( M, X ), состоящей из замкнутого гладкого многообразия M и его подмногообразия X , определена операция взятия следа, которая каждому оператору на M сопоставляет его след — некоторый оператор на подмногообразии X . Следы появились в работах по относительной эллиптической теории (см. [1–3]) и применяются в исследовании задач Соболева с граничными условиями на подмногообразиях произвольной размерности. В последнее время интерес к следам возник в связи с тем, что следы дают операторы новой природы. В частности, исследовались следы операторов, ассоциированных с действиями групп Ли G на основном многообразии M (такие операторы будем ниже называть G -операторами, см. [4]). Было установлено, что такие следы в общем случае уже не являются G -операторами, а локализованы на некоторых подмножествах подмногообразия X . Соответствующие общие теоремы о локализации получены в работе [5]. В работе [6] исследованы следы, которые сосредоточены на конечном множестве точек — неподвижных точек действия группы. В этой ситуации для следов (которые оказываются операторами Фурье–Меллина) была установлена теорема конечности и предъявлена формула индекса.

В настоящей работе рассматривается случай, когда неподвижные точки действия группы образуют подмногообразие произвольной размерности, вложенное в данное подмногообразие X . В этом случае основная теорема настоящей работы утверждает, что след G-оператора представляет собой псевдодифференциальный оператор с операторно-значным символом, причём для любого значения параметра этот символ является оператором Фурье–Меллина, изученным нами ранее. Этот результат даёт в качестве следствия теорему конечности. Однако, работая с символом — оператором Фурье–Меллина, мы уже не можем говорить о естественных условиях, при которых он обратим, а только об условиях, при которых он фредгольмов. Мы также рассматриваем ситуацию, когда символ не является обратимым, а является только фредгольмовым. В этом случае задача не является фредгольмовой. Однако её можно достроить до фредгольмовой задачи, пользуясь техникой оснащений, разработанной Б. Ю. Стерниным. Эта техника заключается в том, что если к данному псевдодифференциальному оператору с фредгольмовым операторно-значным символом добавить конечное число граничных и кограничных условий, этот оператор становится фредгольмовым (см. [7]). Мы применяем эту технику и строим оснащения следа G-оператора.

2.    Постановка задачи

Рассматривается гладкое замкнутое многообразие M , замкнутое подмногообразие X с гладким вложением i : X —> M коразмерности v и компактная группа Ли G , гладко действующая на многообразии M .На M рассматривается G -оператор (см. [4]):

D =

G

D g T g dg,

где D g — семейство псевдодифференциальных операторов порядка m , гладко зависящее от g ∈ G , T g — оператор сдвига, индуцированный действием элемента g ∈ G :

Tg u (x) = u (д1 x), dg — мера Хаара на группе G.

Цель настоящей работы состоит в том, чтобы исследовать оператор i!(D) = i* Di* : Hs(X) ^ Hs-m-v(X),

который называется следом оператора D на подмногообразии X (см. [1]), где i ^∗ и i _∗ — операторы ограничения и коограничения, отвечающие вложению X → M . Напомним, что оператор ограничения i ^∗ действует непрерывно в пространствах

i* : Hs (M) ^ Hs- 2 (X), s - v/2 > 0, и сопоставляет функции на многообразии M ее ограничение на подмногообразие X : i*(u) = ulx, а оператор коограничения i*, определяемый двойственным образом к оператору i∗ , действует непрерывно в пространствах

i* : H-s + 2 (X) ^ H-s(M), -s + v/2 < 0, по формуле i* (u) = u®5x, где 5x — дельта-функция на подмногообразии X. Таким образом, след (1) корректно определен при s < 0, s — m — v > 0.

3.    Действие группы вблизи неподвижного подмногообразия

Введем некоторые условия на действие группы G по отношению к подмногообразию X , в которых, с одной стороны, потребуем, чтобы неподвижные точки действия группы G образовывали подмногообразие в X , и, с другой стороны, наложим некоторые условия трансверсальности.

Пусть X ^G = {x Е X | gx = x Уд E G} — множество неподвижных точек на X и G X = {д Е G | 3x е X \ X G : gx Е X} — множество элементов группы G , которые оставляют внутри X другие точки, кроме неподвижных.

Определение 3.1. Действие группы G будем называть допустимым , если

• 2)    множество G x состоит из конечного числа элементов, и для любого элемента g Е G x имеем gX = X , где gX — образ многообразия X под действием элемента группы g .

Пример 3.2. На рис. 1 изображен пример, когда M = R ³ , X = R ² , группа G действует поворотами вокруг прямой X G = R ¹ , лежащей в X .

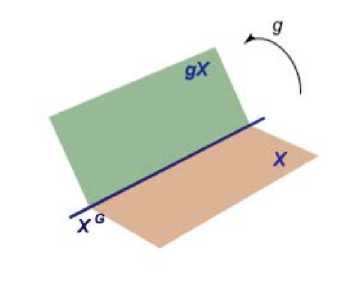
Рис. 1. Многообразия X , gX , X G . Объемлющее пространство соответствует многообразию M

Пусть N — нормальное расслоение над многообразием X G , отвечающее вложению X G G M . Далее будем отождествлять окрестность нулевого сечения в N с некоторой трубчатой окрестностью U С M подмногообразия X G в многообразии M с помощью фиксированного диффеоморфизма.

Пусть N e — нормальное расслоение над многообразием X G , отвечающее вложению X G G X . Оно является подрасслоением расслоения N , и окрестность нулевого сечения в нем также диффеоморфна некоторой трубчатой окрестности подмногообразия X ^G , теперь уже в многообразии X . Будем считать, что последний диффеоморфизм отвечает фиксированному выше диффеоморфизму в следующем смысле: диаграмма

N -G U

↑↑            (2)

N e -G X П U

(вертикальные стрелки обозначают вложения соответствующих пространств, а горизонтальные — указанные выше диффеоморфизмы) коммутативна.

Будем также считать, что в окрестности U действие группы G является послойно линейным по отношению к структуре векторного расслоения N G X G .

Для упрощения вычислений введем еще ограничение на размерности подмногообразий. А именно, будем считать, что выполнено соотношение codim м X G = 2codim х X G.

На многообразии M в окрестности точки на подмногообразии X G построим специальные координаты, которые будут использоваться в дальнейшем. Для этого зафиксируем элемент g Е G \ G x . Пусть N g — нормальное расслоение подмногообразия X G , отвечающее вложению X G G gX 1 , Тогда из условия трансверсальности пересечения X G = X П gX следует разложение

TMIXG = TXG ф Ne ф Ng расслоения TM|хg G XG в прямую сумму векторных расслоений. Следовательно, в силу коммутативности диаграммы (2), для любой точки из XG существуют ее окрестность в M и координаты (у, z, zg), в которых подмногообразие XG задается уравнением {(z, zg) = (0, 0)}, многообразие X — уравнением {zg = 0} и многообразие gX — уравнением {z = 0}.

Все перечисленные в этом пункте условия в совокупности будем называть условиями допустимости и считать в дальнейшем всегда выполненными.

4.    Анализ структуры следа оператора

Начнем со следующего выражения для следа:

i ^! D = i * Di * = j i * D g T g i * dg = j i * D g i gx * T g dg

(мы прокоммутировали операторы T g и i _∗ ), где i _gX _∗ для каждого фиксированного g — оператор коограничения с подмногообразия gX — образа подмногообразия X под действием элемента g . Действительно, T g i * = T g i * T - 1) T g = i gX * T g , где второе равенство следует из определения оператора коограничения.

Теперь наша задача разбивается на две части: изучить оператор, стоящий в (3) под знаком интеграла, и затем изучить оператор, который представляется как интеграл от семейства таких операторов.

4.1.    Подынтегральное выражение

Итак, под знаком интеграла в (3) имеем оператор

i * D g i gX * : H s ( gX ) -^ H s - m - ( X ) .

Операторы такого вида называются трансляторами и изучались в работах [8–10, 14]. (Отметим, что терминология и первые работы о трансляторах принадлежат Б. Ю. Стернину (см. [7])). В частности, в работе [9] изучались трансляторы, отвечающие двум многообразиям, которые пересекаются трансверсально по некоторому гладкому подмногообразию. При наших условиях на действие группы при g Е G \ G x мы находимся именно в такой ситуации и потому можем применить результаты работы [9].

В частности, из цитированной работы следует, что оператор i∗DgigX∗ является псевдо-дифференциальным оператором с операторно-значным символом (см. [11, 12]). Поскольку такие операторы технически трудно изучать в пространствах Соболева, мы, прежде чем формулировать какие-либо утверждения, заранее приведем оператор i∗DgigX∗ к оператору нулевого порядка. Положим s-m-ν                 s

Ag = А X 2 i*Dg igX * AgX : L 2( gX) -^ L 2( X), где Ax и Agx — операторы Лапласа на многообразиях X и gX соответственно.

Мы будем рассматривать оператор A g как псевдодифференциальный оператор с операторно-значным символом, т.е. как оператор, действующий в сечениях гильбертовых расслоений, которые будут сейчас определены. Пусть N g — гильбертово расслоение над X G со слоем L ² ( N g,y ) (см. [12], с. 74), где N g,y — слой расслоения N g над точкой у Е X G . Имеется естественный изоморфизм

L ² ( N g ) - L ² ( X G , N ) .                                 (4)

Далее, оператор i∗DgigX∗ сосредоточен на подмногообразии XG (напомним, что оператор C сосредоточен на подмногообразии XG , если для любой гладкой функции ϕ с носителем вне этого подмногообразия композиции Cϕ, ϕC являются компактными операторами). Отсюда следует, что, пренебрегая компактными операторами, оператор i∗DgigX∗ (а также оператор Ag ) можно рассматривать как транслятор, отвечающий трубчатым окрестностям подмногообразия XG в многообразиях X и gX. Поэтому, пользуясь диффеоморфизмами из диаграммы (2) и изоморфизмом (4), мы можем с точностью до компактных операторов рассматривать оператор Ag как оператор

A g : L ² X ^g , N g) -^ L ² ( X ^G , N e) ,

где e — единица группы G . Приведем основные свойства оператора A _g .

Предложение 4.1. Пусть действие группы G допустимо. Тогда для каждого g ∈ G \ GX оператор Ag сосредоточен на подмногообразии XG ⊂ gX и с точностью до компактных операторов является псевдодифференциальным оператором (5), действующим в сечениях гильбертовых расслоений. Символ a(Ag)(y,n) : L2(Ng,y) —> L2(Ney) для каждых (y, n) € TXG равен s-m-ν

^{a (} A g ⁾⁽ y,n ) = ^(A z + n ^{2 ) 2} j e D g

∂∂      s y,z,zg,n, -idz, —idZg) 3g* (Azg + n) 2

где j g : N g,y =^ N y — вложение подмногообразия N g,y в многообразие N y ( слой нормального расслоения к X ^G , соответствующего вложению X ^G ^ M, в точке y ), A z + n ² и A z g + n ² — операторно-значные символы операторов Лапласа A х и A gX соответственно, представленные как операторы с операторно-значимыми символами на подмногообразии X ^G . ²

Доказательство. По построению при всех g ∈ G \ G X оператор A g является транслятором, отвечающим многообразиям X , X _g , которые пересекаются по гладкому замкнутому подмногообразию X ^G , причем их пересечение трансверсально (что следует из условий допустимости и коммутативности диаграммы (2)). Теперь требуемое утверждение есть следствие работы [9]. Предложение доказано.

Замечание 4.2. Символ a ( A g )( y,n ) обладает свойством компактной вариации и свойством скрученной однородности. А именно, разность a ( A _g )( y,n ) — a ( A _g )( y,n 1 ) при всех η, η 1 ∈ T _y ^∗ Y является компактным оператором, и выполнено соотношение a ( A _g )( y,An ) = к \ a ( A _g )( y,n ) к д ¹ , при всех A € R + , где к д u ( х ) = u ( Хх ) — оператор растяжения.

4.2.    Теорема о структуре следа оператора на подмногообразии

Вернемся к оператору (3). Поскольку вместо оператора i∗DgigX∗, фигурирующего в (3), мы стали изучать его приведенную версию (оператор Ag), будем далее рассматривать приведенный след G-оператора D, а именно, оператор i о( D ) = /

G

s-m-ν                s

A g T g dg, где A g = A X ² i * D g i gX * A _gX .

Следующая теорема описывает природу следа G -оператора на подмногообразии и является одним из основных результатов работы.

Теорема 4.3. Пусть действие группы G допустимо. Тогда оператор A = i 0 ( D ) сосредоточен на подмногообразии X ^G ⊂ X; с точностью до компактных операторов является псевдодифференциальным оператором, действующим в сечениях гильбертова расслоения N _e :

A : L² ( X ^G , N e ) —^ L ² ( X ^G , N e )

с символом a ( A )( y,n ) : L ² ( N e,y ) — > L ² ( N e,y ) , ( y,n ) € T*X ^G ,

σ

⁽ A ⁾⁽ y,n ) = /

G

a ( A g )( y,n ) T g dg.

Доказательство. 1. Докажем утверждение о сосредоточенности.

Лемма 4.4. Оператор i 0 ( D ) сосредоточен на подмногообразии X G С X .

Доказательство. В работе [6] дано доказательство в случае, когда X ^G состоит из конечного числа изолированных точек. Доказательство в нашем случае дословно повторяет доказательство из [6].

• 2.    Для доказательства второго утверждения теоремы о псевдодифференциальности сформулируем в виде леммы одно общее утверждение. Введем соответствующие обозначения. Пусть Ф = Ф X G , Ne) — замыкание по норме алгебры псевдодифференциальных операторов, действующих в пространстве L ² ( X G , N e ) сечений гильбертова расслоения N e , со скрученно-однородными символами, 5 — замыкание по норме алгебры 5 гладких символов на S * X G со значениями в ограниченных операторах в слоях расслоения N e .

Лемма 4.5. Пусть B t Е Ф , t Е T, — семейство операторов, равномерно ограниченное по норме и сильно непрерывное по параметру t, лежащему в компакте T . Тогда оператор

B =

T

B t dt,

где dt — некоторая мера на T, является псевдодифференциальным, т.е. B Е Ф, и его символ равен

° ⁽ B >4

° ( B t ) dt.

Доказательство. Отображение ° : Ф — > 5 , D ^ ° ( D ) является гомоморфизмом C * -алгебр, откуда следует, что нормы ||° ( B t ) | | равномерно ограничены (той же константой, что и нормы |B _t | ). Теперь, если мы представим интеграл (7) в виде предела по норме B n ^ B при N ^ го интегральных сумм B n и к каждой из этих сумм применим гомоморфизм ° , то получим, что B — псевдодифференциальный оператор, а его символ равен интегралу символов (8).

• 3.    Вернемся к доказательству теоремы. Заметим, что семейство операторов

  Aε

  
  

  =

  Uε

  
  

  A_gT_gdg,

  
  
5.    Приложения 5.1.    Фредгольмовость

где U _e С G — дополнение к е -окрестности множества G x , сходится к оператору A по норме при е ^ 0, что следует из равномерной ограниченности норм операторов A g и T g .

Теперь, чтобы применить лемму 4.5 к оператору A _ε , нам надо показать, что оператор A g T g является псевдодифференциальным оператором. Вспомним, что оператор A g действует между сечениями расслоений N g и N e , слои которых представлены функциональными пространствами на слоях нормальных расслоений N g и N _e над подмногообразием X ^G . Учитывая, что T _g действует послойно-линейно в слоях расслоения N _g , мы видим, что композиция A _g T _g , очевидно, является псевдодифференциальным оператором между сечениями расслоений N g и N e (его символ представляет собой композицию операторов ° ( A g )( y, п ) и T g ). Обозначая B g = A g T g , мы видим, что выполнены условия леммы 4.5: сильная непрерывность и равномерная ограниченность по норме операторов B g наследуются из аналогичных свойств семейства операторов D g (которыми оно обладает по условию) и сильной непрерывности и равномерной ограниченности нормы семейства T g операторов сдвига.

Итак, оператор А _е является псевдодифференциальным при всех е >  0. Поэтому псевдо-дифференциальным является и оператор A , равный пределу по норме операторов A _ε при е ^ 0. Эти же рассуждения дают искомую формулу для символа.

Теорема 4.3 доказана.

Положим A = i О и рассмотрим оператор

1 + A : L ² ( X ) — > L ² ( X ) .

Следствие 5.1. Пусть символ 1 + ст ( A ) обратим на S * X G . Тогда оператор 1 + A фредгольмов.

Доказательство. Согласно теореме 4.3 имеем A Е Ф, т.е. псевдодифференциальный оператор 1 + A является эллиптическим и, следовательно, фредгольмовым в силу результатов работы [11].

В общем случае символ 1 + ст ( A ) не является обратимым оператором, и говорить можно только о его фредгольмовости. Эта фредгольмовость может быть эффективно проверена, пользуясь результатами работы [6].

Предложение 5.2. Оператор

1 + ст(A)(y,n) : L2(Ne,y)  > L2(Ne,y), для каждых (у, п) Е S*XG является оператором Фурье-Меллина из [6] и не зависит от параметра η с точностью до компактных операторов.

Доказательство. Для фиксированных (у,п) оператор ст(A)(у,п) действует на функциях на слое Ne,y, который вложен в слой Ny расслоения N . В силу условий допустимости, действие группы G на Ney имеет единственную неподвижную точку {0} Е Ny, и для всех точек x ∈ Ne,y орбиты Gx в пространстве N трансверсальны пространству Ne,y. При этом оператор ст(A)(у,п) представляет собой след G-оператора, соответствующего указанной геометрии. Действительно, этот оператор равен ст(A)(У,П) = j ст(Ag)(У,П)Tgdg,

где

^{ст (} A g ⁾⁽ У,П ) = ^(А z ⁺ П ^{2 ) S}

-

m-ν                                   s

² j e D g ⁽ у,п ) ^j g * ^(А Z g ⁺ п 2 ) ²

и операторно-значная функция Dg(у,п) определена так же, как в формуле (6). Преобразуя выражение (10) и подставляя его в (9), получаем ст(A)(У,П) = j* j (Аz + П2)s

-

m-ν                          s

² D g ⁽ У,П ^)(А z g + П ^{2 ) 2} T g dgj * ,

где j — вложение N ey ^ N y . Пользуясь свойством компактной вариации символа ст ( A ), мы можем положить в формуле (10) п = 0. Имеем (с точностью до компактных операторов):

ст ( A )( у,п ) = j* j А z

-m-ν

s

2 D g ⁽ У,П ^)А zg² T g dgj * ,

т.е. ст ( A )( у,п ) действительно представляет собой след G -оператора:

B ( у,п ) = /

G

А

s

-

m

z

ν

- ^s

D g ( У,П ) А z g² T g dg,

порядок которого, как видно из (11), равен ord B ( у,п ) = —v .

Итак, согласно работе [6], оператор 1 + ст ( A )( у,п ) является оператором Фурье-Меллина для каждого ( у,п )■ Независимость от значения параметра п следует из компактной вариации для 1 + ст ( A ).

Символ оператора Фурье-Меллина 1 + ст ( A )( у,п ) обозначим ст ₇ [1 + ст ( A )( у,п )]( p ). Он определен как аналитическая оператор-функция на прямой

Re p = ү, где ү = dim N _e,_y / 2 = codim X X ^G / 2 = codim M X ^G / 4

(оператор 1 + ст ( A )( у, п ) действует в пространствах L ² на линейном пространстве N ey , размерность которого равна коразмерности вложения X ^G ^→ X ).

5.2.    Оснащения

Пусть

P : L ² ( Y, H 1 ) -^ L ² ( Y, H 2 )

• — псевдодифференциальный оператор на гладком замкнутом многообразии Y , действующий между сечениями гильбертовых расслоений H 1 и H 2 над Y . Предположим, что символ ст ( P ) является семейством фредгольмовых операторов.

Определение 5.3. Оснащением оператора P называется фредгольмов оператор вида

PD,\

L ² ( Y, H1 )        L ² ( Y, H 2 )

⊕    -→     ⊕   ,

L ² ( YE )        L ² ( Y, F )

где E , F — некоторые конечномерные векторные расслоения над Y , B , C , D — некоторые псевдодифференциальные операторы.

Утверждение 5.4. [10]. Пусть символ оператора P обладает свойствами компактной вариации и скрученной однородности. Тогда оснащение оператора P существует, т.е. можно подобрать подходящие расслоения E, F и операторы B, C, D .

Вернемся к многообразию X G и оператору 1 + A на нем. Напомним, что оператор A является псевдодифференциальным оператором, действующим в пространствах

1 + A : L2(XG,Ne) -^ L2(XG,Ne), с операторно-значным символом 1 + ст(A) : n*Ne —> n*Ne, где п : S*XG —> XG— естественная проекция.

Потребуем, чтобы символ 1 + ст ( A ) был эллиптическим оператором, т.е. символ Фурье-Меллина Ст ү [1 + ст ( A )( y,n )]( p ) был обратимым оператором для всех

( y,n,p ) € S * X G х { Re( p ) = 7}, ү — codim m X G / 4 .

Тогда по утверждению 5.4 существует оснащение оператора 1 + A , т.е. такие векторные расслоения E , F над X ^G и операторы b, c, d на S ^∗ X ^G , что оператор

/ 1+ ст (A) с\   n*Ne ст (B) —                  : ф   —> ф(12)

bdπ∗Eπ является обратимым. Определим псевдодифференциальный оператор

B : L2 (XG, Ne ф Е) -^ L2 (XG, Ne ф F)

с символом (12). По построению этот оператор фредгольмов. Итак, мы получаем

Следствие 5.5. Оператор (13) , являющийся оснащением оператора 1 + A, корректно определен ( является псевдодифференциальным оператором с операторно-значным символом ) и эллиптичен.

Пример 5.6. Пусть символ 1 + ст ( A ) является семейством фредгольмовых операторов. Тогда все операторы 1 + ст ( A )( y,n ), ( У,П ) € S*X G , имеют конечные ядро и коядро. Предположим, что эти ядра и коядра образуют конечномерные векторные расслоения

Ker ^ S * X G , Coker ^ S * X G .

Пусть все операторы 1 + ст ( A )( y,n ) являются мономорфизмами (т.е. у них отсутствует ядро), и имеются векторное расслоение E над X G и изоморфизм с : п*Е —> Coker , тогда символ

π ^∗ N e

(1 + ст ( A ) с ) : ф   —> n*N e

π∗E можно взять в качестве символа оснащения оператора 1 + A. Иначе говоря, оператор 1 + A превращается во фредгольмов оператор путем добавления кограничных условий.

Если же мы предположим, что все операторы 1 + ст ( A )( у,п ) являются эпиморфизмами (т.е. у них отсутствует коядро), и пусть имеются векторное расслоение F над X ^G и изоморфизм b : Ker — > п * Е. Тогда оператор

( ^{1 +} ^ ^{( A} ) } : n * N e —^

n * N e ® _π ∗ _F

определяет символ оснащения оператора 1 + A . Таким образом, в этом случае оператор 1 + A превращается во фредгольмов оператор путем добавления граничных условий.

6.    Пример

Рассмотрим тор M = T3 с локальными координатами (y, z, t) и вложенный в него тор X = T2, задаваемый уравнением {t = 0}. Предположим, что на объемлющем торе M действует группа G = S1 вращениями вокруг окружности {z = 0, t = 0}, а именно, элемент ф Е G действует на точку x = (y, z, t) как умножение на матрицу x ।—>   0

cos ^ sin ^

— sin ^ cos ^

x.

Многообразие X , сдвинутое под действием вращения на угол ϕ , будем обозначать ϕX .

Действие группы G удовлетворяет условиям допустимости: действительно, в нашем случае множество X ^G неподвижных точек действия группы G задается уравнениями {z = 0 , t = 0 } и является подмногообразием в X , а множество G x “особых” точек группы G состоит из двух элементов: 0 и п ; все остальные условия (трансверсальности и т.д.) очевидны из определения.

Далее, подразумевая локальное рассмотрение, многообразия M , X и X ^G будем отождествлять с пространствами R ³ , R ² и R соответственно, с теми же координатами ( y,z,t ). Тогда геометрическая картина выглядит так: в пространстве R ³ фиксирована плоскость, и группа G действует вращениями вокруг прямой на этой плоскости (см. рис. 1).

Рассмотрим G -оператор D :

D = Д-1 f T^dp : Hs(M)   - Hs+2(M), где Д — оператор Лапласа на M. Тогда след i! (D) этого оператора на подмногообразии X равен i!(D )=/ i* Д -1 T^i*dv : Hs (X)   - Hs+1( X)

и корректно определен при s < 0 и s + 1 > 0. Приведенный след равен i0(D) = / ДX+1 [i*Д-1 T^i*] ДX2dV : L2(X)    - L2(X), где Дx — оператор Лапласа на многообразии X, и изучим оператор вида

1+ i 0 ( D ) : L ² ( X ) —^ L ² ( X ) .

По теореме 4.3 оператор 1 + i o ( D ) является псевдодифференциальным оператором на многообразии X G с операторно-значным символом, который для каждого у Е X G является оператором, действующим на функциях в L ² ( N _y ), где

N y = { ( z, t ) I t = 0 } — {у = 0 , t = 0 } C R ³ .

Вычислим символ оператора (14). Для этого зафиксируем y , применим оператор (14) к функции u ( z ) G L ² N y ) и сделаем преобразование Фурье по у :

[ 1 + ст ( i 0 D ⁾⁽ у, п )] u ⁽ z ) = u ⁽ z ^{) +}

+

[^{2 П} (А z

J о

s +1                                             _- s

+ П 2 ) ² j * [( П ² + А z,t ) - ¹ Т ^\ j * (А z + п ² ) ² u ( z ) dy,

где А _z,t — оператор Лапласа на многообразии R 2 t — {у = 0 } , А _z — оператор Лапласа на многообразии R _z — {у = 0 , t = 0 } , j : R _z ^ R 2 _t — вложение многообразия {у = 0 , t = 0 } в многообразие {у = 0 } , п — двойственная переменная к у .

Утверждается, что для каждых фиксированных ( у, п ) оператор (15) — это оператор Фурье–Меллина на подмногообразии R _z . В самом деле, поскольку символ обладает свойством компактной вариации, мы можем положить п = 0. Обозначим

1 + A = 1 + ст^і 0 D )( у, 0)

и изучим этот оператор.

Далее, следуя [6], получим действие оператора A после преобразования Фурье по переменным ( z, t ):

(1 + A ) u ( Z ) = u ( Z ) +

2 п

0 R t

IZ| s ⁺¹        u ( Z cos y + T sin y )

IZ cos y + T sin y| ^s        Z ² + T ²

dϕdτ,

где ζ , τ — двойственные переменные к z , t . Сделаем в последнем интеграле замену переменной t ^ Ө по формуле Ө = Z cos y + t sin y . Получим

(1 + A ) u ( Z ) = |Z|u ( Z ) + yR Kr( Z,Ө ) u ( Ө ) Ө,

где интегральное ядро Kr( Z, Ө ) равно

2 п

Kr( Z,Ө )= /

Z s |Z ||Ө|| sin y|                   ( ^s IZI + |Ө|

Ө Z ² + Ө ² - 2 ӨZ cos y^y Ө IZ| —|Ө|

Разобьем функцию u ( Z ) в сумму u ( Z ) = u ⁺ ( Z ) + u - ( Z ) , где u ⁺ ( Z ) — четная компонента и u - ( Z ) — нечетная. Тогда оператор (16) по отношению к указанному разбиению на четную и нечетную компоненту записывается в матричном виде:

_{(1 + i)} / u + ( < ) V f1+4 .Гк Ш d»

^{(1 +} A ) V u - ( Z ) у = I          ^0o ₀ ^^Ie^ ^|Ө|

0     / u ⁺ ( Z )

1 ) V u - ^{( Z} )

где

K ( t ) = ! t s in I l± t

П 1 — t

Преобразование Меллина (см., например, [13]) M r , p u ( r ) = Jr+ t p u ( t ) dt/t переводит оператор (17) в оператор умножения на матрицу:

/ _tg / T i p +l A    \

_{(1 +} A f ^{u + (} p ) A =   1 + 4 n —Ц— L 0   ( u ^{+ (} p ) A

Z u - ( p ) J                p ⁺ s          \ u - ( p ) .

\         0          1У

Эта матрица и есть символ Фурье–Меллина оператора A , который обозначается через ст 1 / 2 (1 + A )( p ). Отметим, что здесь выбирается весовая прямая Re p = 1 / 2, так как оператор A действует в пространствах L ² ( X ), поэтому, согласно определению символа оператора Фурье-Меллина (см. [6]), весовая прямая имеет вид Re p = codim х X G / 2 = 1 / 2 .

Предложение 6.1. Оператор (15) фредгольмов при тех s, для которых tg П^ П+Г) = - -   - г’ -1

\ \ 4   2у)     8 п 4 п

Доказательство. Матрица ст i / 2 (1 + A )( p ) вырождена, когда выполнено равенство

( p + s ) = 4 п tg ( п ( p + s ) / 2) .

Представим p + s в виде p + s = a + ів , где а и в — вещественные числа (при этом а = 1 / 2+ s ), и рассмотрим мнимую часть уравнения (19). Получим соотношение

1 в = sh пв

4 п    cos па + ch пв

Заметим, что левая и правая части равенства (20) для каждого α являются нечетными функциями переменной β , при этом для ненулевых β они принимают значения противоположных знаков. Поэтому равенство (20) выполнено только при в = 0. Отсюда следует, что соотношение (19) не выполнено никогда, если у p присутствует мнимая часть. Подставляя в (19) p = 1 / 2, получаем условие (18).

Работа выполнена при поддержке Российского фонда фундаментальных исследований (РФФИ), проекты № 16-31-00176, № 16-01-00373.