О спектральных свойствах самосопряженных частично интегральных операторов с невырожденными ядрами

Линейные уравнения и операторы с частными интегралами возникают в различных областях механики [1–4], теории интегро-дифференциальных уравнений [5, 6], теории операторов Шредингера [7–9] и в ряде других прикладных задач [10–12]. Частично интегральные операторы T 1 и T 2 действуют в пространстве функций с двумя переменными x Е Q i и y Е Q 2 , где Q i и Q 2 являются замкнутыми линейно связанными ограниченными множествами в R ^V 1 и R ^v 2 , соответственно. Оператор T i интегрирует функцию f ( x,y) по аргументу x G Q i на множестве Q i , а оператор T 2 интегрирует функцию f ( x,y) по аргументу у Е Q 2 на множестве Q 2 . Обычно операторы T i и T 2 являются ограниченными, но не являются компактными операторами. Последнее обстоятельство вызывает интерес

• © 2022 Култураев Д. Ж., Эшкабилов Ю. Х.

• 2.    Необходимые сведения и предложения

специалистов к исследованию спектров операторов T i , T 2 и T i + T 2 . Легко проверяется равенство T i T 2 = T 2 T i , и T i T 2 является компактным интегральным оператором.

В [13] изучен спектр ЧИО (частично интегрального оператора) T i + T 2 в L 2 с положительными ядрами. Затем в 1991 г. А. С. Калитвин и П. П. Забрейко [14] исследовали спектральные свойства частично интегральных операторов вида T i + T 2 в пространстве L p, p ^ 1 . Линейные операторы и уравнения с частными интегралами в разных функциональных пространствах исследовались в монографиях [11, 12], см. также [15].

В работе [16] исследованы существенный и дискретный спектры суммы тензорных произведений самосопряженного компактного оператора и тождественного оператора в гильбертовом пространстве L 2 . В статье [17] изучаются спектральные свойства ЧИО T 1 с ограниченным ядром. Затем в гильбертовом пространстве L 2 (Q i х Q 2 ) изучены спектральные свойства самосопряженных ЧИО T i , T 2 и T i + T 2 с непрерывным ядром трех переменных и доказана теорема, описывающая свойства существенного и дискретного спектра ЧИО T i + T 2 [18]. Доказана теорема о дискретном спектре для самосопряженного ЧИО Н о — (T i + T 2 ) с непрерывным ядром в [19], где Н о — оператор умножения на непрерывную функцию.

В работе [20] получено явное выражение для существенного спектра и доказано существование собственного значения ЧИО Н о — (T i +T 2 ) c ядром трех переменных (в частном случае, сокр. ЧИО). Исследованы существенный и дискретный спектры самосопряженных ЧИО T i , T 2 и T i +T 2 типа Фредгольма в пространстве L 2 ([a, b] х [c, d]) с вырожденным ядром в [21].

Несмотря на ряд публикаций о спектрах ЧИО, отсутствуют теоремы о точном описании существенных спектров самосопряженных ЧИО, возникающих в прикладных задачах. В данной статье, в гильбертовом пространстве L 2 ([a, b] х [c, d]) изучаются спектральные свойства самосопряженных ЧИО типа Фредгольма T i , T 2 и T i + T 2 с невырожденными ядрами. Дано точное описание существенных спектров операторов T 1 и T 2 (§ 3). Получено явное описание существенного спектра ЧИО T i + T 2 и изучено существование счетного числа собственных значений в дискретном спектре ЧИО T i + T 2 с невырожденным ядром (§ 4).

Пусть T i — линейный интегральный оператор в пространстве L 2 ([a, b] х [c, d]) , заданный по формуле

b

^(T i f^)(x,y) = j ^k(x,s,y^{)f (s,}y) ds.

a

Здесь k(x,s,y) измеримая функция в смысле Лебега на [a, b] ² х [c, d] и интеграл в (1) понимается в смысле меры Лебега на [a, b].

Ядро k(x,s,y) интегрального оператора T i обычно удовлетворяет условию

b j k(x,s,y)f (s, y) ds G L2([a, b] х [c, d]), Vf G L2([a, b] х [c, d]). a

Следовательно, оператор T 1 является линейным ограниченным оператором на

L 2 ([a, b] х [c,d]) . Если, кроме того, ядро k(x,s,y) удовлетворяет условию

k(x,s,y) = k(s,x,y) для почти всех x, s G [a, b] и y G [c, d], тогда оператор T1 является самосопряженным оператором в гильбертовом пространстве L2([a, b] x [c, d]).

Пусть H — сепарабельное гильбертово пространство, A : H ^ H — линейный ограниченный самосопряженный оператор. Через a(A) , a ess (A) и a disc (A) обозначим, соответственно, спектр, существенный спектр и дискретный спектр самосопряженного оператора A (см. [22, 23]).

Введем также следующие обозначения:

E min (A) = inf { A : A G C ess (A) } ,   E max (A) = SUp { A : A G C ess (A) } .

Число E min (A) G a(A) ( E _max (A) G a(A) ) будем называть нижним краем (верхним краем) существенного спектра оператора A .

Для существенно ограниченной измеримой функции V ^ 0 на измеримом множестве

Q С R ^v мы определим [24]

esssupQ(V) = inf {C : ц({< G Q : v(€) > C}) = 0}, где ^0 мера Лебега на R. Для измеримой функции V на множестве Q С Rv, число A G R называется [24] существенным значением функции ϕ, если

00 G Q : A — е < v(^) < A + е}) > 0, для всех е > 0. Обозначим через essran(^) множество всех существенных значений функции ϕ.

Пусть { V k (x) } k =! — полная ортонормированная система функций из L 2 [a, b] и пусть { h k (у)}0 1 — система существенно ограниченных измеримых вещественных функций на [c, d] . Определим измеримую функцию k i (x,s,y) на [a, b] ² x [c, d] с помощью следующего правила:

∞ ki(x,s,y) = ^Vk(x) Vk(s) hk(y),                             (2)

k =1

где | h k (y) | ^ M k, k G N и ^ k =1 M k = M <  to .

Предложение 1. Частично интегральный оператор T с ядром k i (x,s,y) (2) является самосопряженным ограниченным линейным оператором на L 2 ([a, b] x [c, d]) .

• <1 Линейность и самосопряженность интегрального оператора T с ядром (2) проверяется легко. Мы докажем ограниченность оператора T 1 . Имеем

  T i f ^(x,y) = I

  a

  
  

∞∞

^ V k ^(x) V k ^(s) h k ⁽ y ) f ^{( s,} y ) ^ds = ^T k ^{(1) f (х,}У), k =1                                 k =1

где

b

T k ' f (x, y) = У V k (x) V k (s) h k (y)f (s, y) ds, k G N. a

Пусть f G L 2 ([a, b] x [c, d]) . Тогда для каждого интегрального оператора T^; , k G N , используя неравенство Коши — Буняковского, получим

b

|^T k ^{(1) f (x,}y) I <  Ih k ⁽y) I |V k ^(x)|

j ^{1 f (s,}y^{) | 2} ds.

a

Следовательно,

b   db

||Ti(1) f||2 < / |vi И2 dx I\hk (y)|2/If (s,y)|2 dsdy C Ml l|f |2, a   ca

k E N.

Тогда ||T i f || C M ||f ||. Таким образом, оператор T i является ограниченным оператором в L 2 ([a, b] х [c,d]) . Предложение 1 доказано. >

Рассмотрим следующие ортогональные проекторы P i, k E N , в пространстве

L 2 ([a,b] х [c,d]) :

b

P i ^{f (x,} y ) = I

V i (x) V i (s) f (s, y) d^ i (s),

k E N.

a

Предложение 2. Пусть E — тождественный оператор в пространстве L 2 ([a, b] х [c, d]) . Тогда P i + P 2 + ... + P n + ... = E.

<1 По предположению { v n (x) } n =i — полная ортонормированная система в L ₂ [a,b] -Для каждого f (x,y) E L ₂ ([a, b] х [c, d]) имеем f (x,ш) E L ₂ [a, b] при п. в. ш E [c, d] и, пользуясь свойством ряда Фурье в гильбертовом пространстве L 2 [a, b] , получим

^

f(x, ш) = ^c n (w )< V n (x) прип.в. ш E [c,d],                     (3)

n =1

где

b

C n (ш) = У f (х,ш) V n (x) dx, a

ш E [c, d].

Из (3) получим, что

lim n^^

где f _ш (x) = f (x,ш) .

Отсюда имеем

Таким образом, для

n

52 c j ^(ш)v j - ^f ^

j =1

lim n^^

каждого

E^ =1 c n (y)V n (x). Отсюда

= 0 при п. в. ш E [c, d], L 2 [ a,b ]

n

52 c j V j - ^f ^ j =1

= 0.

L 2 ([ a,b ] x [ c,d ])

f (x,y) E L ₂ ([a, b] х [c, d]) верно равенство f (x,y) =

f(x,y)

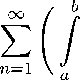
f (s,y) V n (s) ds

)

^

V n ^(x) = 52 P i ^{f (x,}y⁾, n =1

т. е. En =i P l = E . Предложение 2 доказав. >

Предложение 3. Для спектра ^(T i ) ЧИО T i с невырожденным ядром k i (x, s, y) (2) , справедливо включение

^

^J essran(h i ) C ^(T _i ).

i =i

Предложение 4. Число А д = 0 является собственным значением оператора T i тогда и только тогда, когда существует j g Е N такой, что ^ 2 ( h — ( { А д } )) > 0 .

Предложение 5. Любое собственное значение А = 0 ЧИО T i является бесконечно кратным.

Доказательства предложений 3, 4 и 5 аналогичны доказательствам теоремы 2.3, предложений 2.1 и 2.4 из [21], соответственно.

• 3.    Спектр частично интегрального оператора Ti

В этом параграфе будем исследовать спектр ЧИО T i с невырожденным ядром (2).

Предложение 6. Имеет место свойство 0 Е a(T i ) .

• <1 Пусть А к Е essran(h k ) = 0 , к Е N . Тогда А k Е ^(T _i ) , к Е N . Так как ряд ^ k =i M k сходящийся, то lim^ ^ M k = 0 . В силу | h k (y) | ^ M k , к Е N , имеем lim^ ^ h k (y) = 0 при почти всех у Е [c, d] . Следовательно, для последовательности чисел А k Е a(T i ) , к Е N , имеем lim k ^^ А k = 0 . Из предложение 3 и в силу замкнутости спектра a(T i ) вытекает, что 0 Е ff ( T i ) . Предложение 6 доказано. >

Предложение 7. Если А Е C \ ( { 0 } U Ufc =i essran(h k )) , то оператор T i — АЕ обратим в L 2 ([a, b] х [c, d]) , а оператор (T i — АЕ) ^{- i} ограничен в L 2 ([a, b] х [c, d]) , более того,

( T i — АE) ^{- 1} f (x,y) =

А (f^(Х,У) Е h k (y)У - А^{P k} f ^(Х,У)) •

< Сначала докажем ограниченность оператора (T i — АЕ) ⁱ . Пусть А Е C \ ( { 0 } U U ^ =i essran(h k )) . Рассмотрим линейный оператор B :

Bf (х,У)

∞

Е k=i

¹ р \ ₌ 1 ^Е МуНЛе-Еу) h k (у) — А ^k f ^{( ,У)}   А k =i      h k (y) - А

P k f ^(x,y)

λ

∞∞

—Е Pkf (x,y)+Е k=i            k=i

h k (y) h k ^{(y) — А}

P k f (x, y)

^{f (x,y)} Е h _k (y)' — а^{Р f (x,y)}

Определим в L 2 ([a, b] х [c, d]) линейный оператор A :

∞

Af (x,y) = Е T^f (x,y), k=i где

b

TEf (x,y)= / Th^Mr ^k(x) ^k(s) f (s,y) ds, k Е N. k            J hk(y) — А a

Пусть f Е L 2 ([a, b] х [c, d]) — произвольная функция. Тогда для интегральных опера- (2)

торов Tk , к Е N , используя неравенство Коши — Буняковского, получим

|T k ⁽²⁾ f(x,y)| ² <

h k (y) h k ^{(y) — А}

b

kk ^{(x) |2}y^{| f(s,}y^{) |}

² ds.

a

Так как А G C \ ( { 0 } U Ufc =i essran(h k )), то существует число c >  0 такое, что

|hk (y) — А| ^ c при почти всех y G [c, d], k G N. Тогда имеем bd

^^ = / I ^f (x,y)l2dxdy ac

b

<>

bd

² .                  M 2

| f(s,y) | dsdy ^ —k ||f ||² ,

V k G N.

a

ac

Следовательно, ||Af || ^ MM||f ||. Последнее означает, что оператор A ограничен. Таким образом, оператор B является линейным ограниченным оператором в пространстве L 2 ([a,b] х [c,d]) .

Проверим равенство (T i — АЕ ) B = E . Имеем

ГО 1

Bf ^(x,y) = ^"ТЛ Г Pf ^{( x,} y ) . tl h h ^{k (} y ) ^{— А}

Положим g ( x,y) = Bf ( x,y ) Тогда

∞

^(T i ^{— A} E ^{) Bf ( x} , y ) = ⁽ T i ^{— A}E)g^(x, y ) = ^ ( h-k ⁽ y ) ^— X PPggxx, y ) k =i

∞

= ( h i ( y ) — A)P 1 £

- j=i

P j fxy ) h j ^{( y ) — А}

∞

+ . . . + ^(hn^{(y) — A)P}n ^^

j =i

P j ^{f ( x,} y ) ^h j ^{( y ) — А}

+ ...

∞

∞

= ^2^P k ^{2f ( x,y} ) = ^P k ^{f ( x,y} ) = ^{f ( x,} y Y k =i              k =i

Следовательно, (T i — AE)B = E .

Аналогично легко показать, что B ( T i —АЕ) = Е . Таким образом, оператор B является обратным оператором для оператора T i — АЕ , т. е. (T i — AE) ^{- i} = B . Предложение 7 доказано. >

В силу предложений 3, 5, 6 и 7 справедлива следующая теорема.

Теорема 1. Для спектра a(Ti) ЧИО Ti с невырожденным ядром ki (2) справедлива формула

a(T i ) = a ess (T i ) = { 0 } U

∞ и k =i

essran(h k )

)

Для ЧИО T i с вырожденными ядрами аналоги теоремы 1 доказаны в работе [21]. Пусть T2 — линейный интегральный оператор в пространстве L 2 ([ a, b ] х [c, d]) , заданный по формуле

^(T 2 ^f K^y)

d j q(x,t,y)f (x,t) dt.

c

Здесь q ( x, t, y ) — измеримая функция в смысле Лебега на [a, b] х [c, d] ² и интеграл понимается в смысле Лебега на [ c, d ] .

Ядро q(x, t, у) интегрального оператора T 2 обычно удовлетворяет условию

d j q(x,t,y)f (x,t) dt E L2([a, b] x [c, d]), V f E L2([a, b] x [c, d]).

c

Следовательно, оператор T 2 является линейным ограниченным оператором на

L 2 ([a, b] x [c, d]) . Если, кроме того, ядро q(x,s,y) удовлетворяет условию

q(x,t, у) = q(x,y,t) для почти всех x E [a, b] и y,t E [c, d], тогда оператор T2 является самосопряженным оператором в гильбертовом пространстве L2([a,b] x [c,d]).

Пусть { c j (y) } j =i — полная ортонормированная система функций из L 2 [c, d] и пусть {P j (x) } 5 =i — система существенно ограниченных измеримых вещественных функций на [a, b] . Определим измеримую функцию k 2 (x,t, у) на [a, b] x [c, d] ² с помощью следующего правила:

∞

М^хЛу) = ^P j ^(x) ^ j (y) ^ j ^(t),                         ⁽⁵⁾

j =1

где | P j (x) | C N j , j E N и 52j =i N j = N <  то . Тогда ЧИО T 2 с невырожденным ядром k 2 (x, t, y) :

d

⁽T 2 ^{f )(x,}y)= j k 2 ^(x,t,y^{)f (x,t) d}№^(t),                        ⁽⁶⁾

c есть линейный ограниченный самосопряженный оператор в L2 ([a, b] x [c, d]).

Аналогичным образом теорема 1 формулируется для ЧИО T 2 .

Теорема 2. Для спектра a(T 2 ) ЧИО T 2 (6) с невырожденным ядром k 2 (x,t, у) (5) справедлива формула

a(T 2 ) = a ess (T 2 ) = { 0 } U

∞ и j =1

essran(p j )

)

• 4.    О спектре частично интегрального оператора Ti + T2

В этом параграфе мы коротко изложим доказательство теоремы о существенном спектре ЧИО T i + T 2 . Надо подчеркнуть, что спектры оператора T i + T 2 с непрерывным ядром исследованы в работе [18], а с вырожденным ядром исследованы в [21].

Предложение 8. Ноль принадлежит существенному спектру оператора T i + T 2 .

• <1 Пусть x o E [a, b] и у о E [c, d ] — фиксированные точки. Для каждого n E N определим подмножества J ^¹ ) С [a, b] и J ^² ) С [c, d] :

  J n¹ ) = {x E [a, b] :

  
  

  < | x - x o | <¹L n + 1             nJ

  
  

  J n^{2 )} = {y ^{E [c,d] :}

  
  

< \У - Уо| < 1} , n + 1            nJ n E N.

Тогда ^ i J n ’ ) > 0 и ^Jn ² ) > 0 для всех n Е N и имеем lim n ^^ ^ i ( Jn ) ) = 0 , lim _n ^^ ^ 2 ( J n 2) ) = 0 . Мы определим следующую последовательность ортонормирован-ных функций ХпЧх) Е L2K b] и X n ²⁾ (y) Е L 2 [c, d] :

x n ’ ^(x) = *

V . J )

.0,

x Е Jn’, x Е Jn’,

х П ^{2) (}У) = *

V. 2 J ² ' ’

.0,

(2) y ^Е J n ,

(2) У / J n •

Определим через f _n (x,y) Е L 2 ([a, b] x [c, d]) , n E N , ортонормированную систему функций f n (x,y) = х П ¹² (х)х П ²⁾ (у) , n Е N . Очевидно, что ||(T i + T 2 )f n | <  H T i f n H + IIT 2 f n | .

Сначала покажем, что lim n ,^ H T i f n H = 0 .

Пусть T ⁰ — ЧИО с ядром k i (x, s,y o ) (см. (2)), заданный по формуле

Тогда

где K y o ’

b

T 0 f (x,y) = j k i ( x,s,y o ) f ( s,y ) ds. a

T 0 f n (x,y) = j . X* (s) x i ?’ (y) ds = (Kg ’ x i i’X x)    (У),

a компактный интегральный оператор, действующий в L2 [a, b] по равенству

b

^K»^V(x⁾⁼ / k ^{i (}x's'^{y 0 ) V(s)} d ^s.

a

Следовательно,

|| T i ^{0 f} n || ² = У ^ K y o ’ x n ’ || ² | x n ^{2) (}y⁾ | ² dy = 11 K y o^ X n"’ ^ L ₂ [ a,b ] ^ ⁰ при n ^^.

J _n

С другой стороны, получим

b

(T i - T 0 ) f n ( x,y ) = j (k i (x,s,y) - k i (x,s,y o )) f n ( s,y) ds

a

b

∞∞

= 52    ( h k ⁽У) - h k ⁽У 0 )) V k ^(x) V k ^{(s) f} n ^(s,y) ^ds = 52^T k ⁽³⁾ f n^ y).

k=ia                                                  k=i где

b

T k ³⁾ f n (x,y) = j (h k (у) - h k (У о )) V k (x) V k (s) f n (s,y) ds, k Е N. a

Отсюда, используя неравенство Коши — Буняковского, получим

^{| T} k ^{(3) f} n ^(x,y^{) |} <  ^{| h} k ⁽y) ^- h k (У 0 ) ¹ ^k ^{(x) |} ^n ² ’ (У) ¹

j ^| V k ^{(s) | 2}

NJn ¹ )

ds .

Следовательно,

IT^^f n (x,y)| 2 ^{С | h} k (y) ^— h k (y o )| 2 ^k (x)| 2 |x n ²⁾ (y)| 2 j | V k ^(s) 1 2 ds, ^{n,k €} N-

! (1)

J _n

Надо отметить, что для каждого k € N имеет место неравенство | h k (y) — h k (y o ) | С 2M k, при п. в. y € J n 2) , так как | h k (y) | С M k , k € N (см. (2)). Таким образом, имеем

bd

^T'^fn^2 = / J \T^fn(x,y)^dxdy ac

bd

С j j (2 M k ) ^{2 |} V k ( x ) ^{|2 |} XnЧy ) ^|2 j^| V k ( s) ^ds dxdy = (2M k V^V k (s) ^ds, n,k € N,

ac т. е.

Jn pk3)fn|| С 2Mk

J _n

| V k (s) | 2 ds, k, n € N.

^ (1)

J _n

Тогда

|| (T i — T0) f n \\ С 2M

j ^| V k ( s ) ^{| 2} ds-

J

В силу абсолютной непрерывности интеграла Лебега, имеем lim n ,^ Jo | V k (s) | 2 ds = 0 для всех k € N , т. е. существует достаточно большое n o € N такое, что /J (i) | V k ( s ) 1 2 ds <  (2M^.n ) 2 k4 при каждом n ^ n o , где E — достаточно малое положительное число. Следовательно,

∞

^(T1 — T10)fn|| С ^ -2- = |C0 ^ 0 при n ^ГО, nn k=1

где C o = ^ k =1 — . Отсюда имеем lim n^ ||( T 1 — T ° )f n | = 0 .

Таким образом, из ||T i f n || С || (T i — Tf)f n | + H T P f n ! получим, что lim n ^^ | T i f n | = 0 . Аналогично докажем, что lim n ^^ | T 2 f _n | = 0 . Следовательно, lim n ^^ | (T 1 + T 2 )f _n | = 0 . Из определения существенного спектра [22, 23] вытекает 0 € a _ess (T i + T 2 ) . Предложение 8 доказано. >

Предложение 9. Имеет место соотношение

_O( T 1 ) U a^) C - . T + T 2 ) -

<1 Мы покажем, что a(T1) C aess(T1 + T2). Пусть Ao € essran(hj0), Ao = 0 и yo — произвольная точка из подмножества h-01({Ao}). Определим через gn(x,y) € L2([a, b] x [c, d]) ортонормированную систему функций: gn(x,y) = Vj0 (x)Xn2)(y), n € N. Доказательство равенства lim ||(Ti — AoE)gn| =0

n→∞ аналогично доказательству теоремы 2.3 из [21].

Для оператора T 2 имеем

∞ ^d                     ∞

T2gn(x,y)   52 Pj(x)^j(y)^j(t^gn(x,t) dt = 52z ' g x-y, j=1 c                                j=1

где

d

Tj^gn^y) = jP j ( x)^ j ( y)^ j ( t ) g n (x,t) dt,  j E N.

c

Нетрудно проверить, что

∞

;'-'-   < £ HTj(4)gn j=1

∞

II ^ £ Nj   j ^j(t)l2dt- j=1    \.

В силу абсолютной не преры вности интеграла Лебега, существует достаточно большое

. 2

n ₀ E N такое, что J (2) | ^ j (t) | ² dt <

J _n

.₄^e_{2 2} при всех n ^ n o , где e >  0 — достаточно малое. j n N _j

Тогда из (8) получим lim n ,' ||T 2 g _n ^ = 0 . Отсюда и из (7) вытекает lim n ,' ll( T i + T 2 — A o E)g _n || = 0 , т. е. по определению существенного спектра A o E a _ess (T i + T 2 ) .

Аналогично получим, что ^(T h ) \ { 0 } С a _ess (T i + T 2 ) . В силу предложения 8 имеем 0 E a _ess (T i + T 2 ) . Предложение 9 доказано. >

Пользуясь предложением 4 и применяя универсальную технику, изложенную в доказательствах утверждений из [21] о спектре ЧИО T i + T 2 с вырожденными ядрами, получим описание существенного спектра самосопряженного ЧИО T i + T 2 с невырожденными ядрами (см. также теоремы 4.2 и 5.4 из [18]). Не повторяя громоздкой процедуры, изложенной в [21], мы сформулируем следующие теоремы.

Теорема 3. Для существенного спектра a _ess (T i + T 2 ) ЧИО T i + T 2 с невырожденным ядром верна формула

CT ess (T 1 + T 2 ) = { 0 } U ^ U essran(h k )^ U ^ ^ essran(p j )^ .

Теорема 4. Пусть выполняются следующие условия для функций h j (y), j E N и P k (x), k E N в ядрах (2) и (5) :

h j (y) >  h j +i (y) > 0, j E N и p k (x) >  P k +i (x) > 0, k E N.

Пусть существуют убывающие последовательности из положительных чисел {a j } j r N и {b k } k e N такие, что

• (i)    V ' a j <  ~ , П =х b k <  ~ ;

• (ii)    max { esssup(h _i ),esssup(p _i ) } = max { a _i ,b _i } ;

• (iii)    h j (y) >  aj- при п. в. y E [c, d], j E N и p k (x) >  b k при п. в. x E [a, b], k E N.

Тогда ЧИО T i + T 2 имеет счетное число собственных значений, лежащих выше верхнего края E _max (T i + T 2 ) существенного спектра a _ess (T i + T 2 ) .

• <1    Пусть V i , V 2 — самосопряженные частично интегральные операторы в пространстве L 2 ([a, b] х [c, d]) с невырожденным ядром, заданные по формуле

∞ ^b                                 ∞ ^d

V i f^(x,y) = 52 a j ^ j ^(x)^ j ^{(s)f (s,}y) ds, V 2 ^{f (x,}y )=52 b k ^ k ⁽y)^ k ^{(t)f (x,t) dt}- j =1 _a                                           k =1 _c

Для существенного и дискретного спектра самосопряженного ЧИО V i + V 2 верны следующие равенства [12]:

^ ess (V 1 ^{+ V} 2 ) = { 0 } U ^{ a j ^} - g N U {b k } k _G N ,

^ disc (V 1 ^{+ V} 2 ) = {^w : ^w = a j + b k ^€ ^ ess ⁽V i + V 2 ), j, k E N}.

Следовательно, ЧИО V i + V 2 имеет счетное число собственных значений, лежащих выше верхнего края E _max (V i + V 2 ) существенного спектра a _ess (V i + V 2 ) , т. е. множество ^ disc (V i + V 2 ) П (E _max (V i + V 2 ) , го ) является счетным множеством.

В силу условий (ii) и (iii) теоремы 4 следует, что E max ( T i + T 2 ) = E _max (V i + V 2 ) и V i С T i , V 2 С T 2 . Тогда из неравенства V i + V 2 С T i + T 2 и леммы 2.2 из [25] ЧИО T i + T 2 имеет счетное число собственных значений, лежащих выше верхнего края E _max (T i + T 2 ) существенного спектра a _ess (T i + T 2 ) . Теорема 4 доказана. >

Пример 1. Пусть [a, b] = [c, d] = [0,1] и для ядер операторов T i и T 2 имеют место следующие равенства:

h i (у) = 2, h j (y) = 4 + e - jy , j € N \{ 1 } и j ²

, ,            , x 1 + sin ⁿ X            , _r

P i ^(x) = 1, P k ^(x) = —2k 2— , ^{k € N} \^{{ 1 }} -

Рассмотрим убывающие последовательности

из положительных чисел { a j } - _g n и { b k } k _G N

a i = 2, a j = j 2 ⁺ e j , j E ^N \ ^{{ 1 }} ,

b i = 1, b k =     , k ^G N \{ 1 } -

2k ²

Тогда в силу теорем 1, 2 и 3 для существенных спектров операторов T i , T 2 и T i + T 2 справедливы следующие равенства:

Л \ г 1  11 Л aess(Ti) = {0, 2}U

I j = ₂ j⁺e j ^; j ^{2 +1}JJ

= [0,4] ^U{ 2 } ,

a ess (T 2 ) = { 0,1 } U

(и

I       2k ²

k =2

k2] ) = [0' 4

U { 1 } ,

σ ess (T i + T 2 ) = σ ess (T i ) U σ ess (T 2 ) =

0,4 и { 2 } .

Из ⁽⁹⁾ вытекает CT ess ⁽V i ⁺ V 2 ) = ^{{ 0,} 1, ^{2 } U} {-2 ⁺ _e ⁱ j }j _G N \_{{ i }} ^U { 2 k 2 }_{k G} N \_{{ i }} . Здесь верно равенство E max (T i + T 2 ) = E max (V i + V 2 ) = 2 .

Таким образом, в данном примере для ЧИО T i + T 2 выполняются все условия теоремы 4. Следовательно, ЧИО T i + T 2 имеет счетное число положительных собственных значений, лежащих выше верхнего края E _max (T i + T 2 ) существенного спектра a _ess (T i + T 2 ) .