О способах повышения точности расчета ударных волн

Для математического моделирования ударных волн в сплошных средах широко применяются однородные разностные методы, в которых ударные волны «размазываются» на несколько интервалов сетки. Неоднородные разностные методы позволяют явно выделять в решении ударные волны в виде разрывов первого рода, которые разграничивают области с гладким решением. Неоднородные методы являются алгоритмически более сложными, но при этом дают возможность на одинаковой сетке получать результаты точнее, чем результаты, полученные с применением однородных методов. Важной особенностью методов с выделением разрывов является отсутствие энтропийных следов в решении.

Одним из первых неоднородных методов, который позволяет выделять в решении сильные и слабые разрывы, был метод характеристик [1, 2]. Метод характеристик использует Эйлеровы координаты.

В 60-х годах создан неоднородный разностный метод в Лагранжевых координатах [3]. Одной из особенностей данного метода является то, что он способен выделять в решении наиболее «важные» разрывы, а остальные разрывы «размазывать». Такая особенность позволяет с успехом применять его для расчета очень сложных течений, акцентируя внимание на определяющих течение областях. Разрывы во второстепенных областях размазываются, что позволяет сократить вычислительные затраты и при этом сохранить точность вычислений.

В данной работе для метода [3] предлагаются способы повышения точности расчета выделенных ударных волн. Для определения величин перед фронтом ударной волны наряду с разностным подходом применяются элементы метода характеристик. Для повышения точности расчета величин за фронтом ударной волны при взаимодействии регулярной сетки и сетки особенностей предлагается алгоритм, позволяющий корректно учитывать возмущения, догоняющие фронт. Для интервалов перед фронтом и за фронтом предлагается подход, который сводит расчет величин в данных интервалах к расчету величин на регулярной сетке.

Шаблон для определения сеточных величин и основные этапы расчета

В данной работе за основу взят неоднородный разностный метод В.Ф. Куропатенко [3]. В этом методе используется разнесенный шаблон - координаты и скорости определены на границах интервалов, а термодинамические величины в их серединах. Будем придерживаться терминологии, используемой в [3]. Интервалы, в которых отсутствуют разрывы, называются регулярными. Интервалы, в которых присутствуют разрывы, называются особыми. Если разрыв попадает в регулярный интервал, то этот интервал становится особым. Когда разрыв покидает данный интервал, он снова становится регулярным. Таким образом, выделенные сильные разрывы рассчитываются как особенности, перемещающиеся по регулярной сетке.

Рассмотрим одиночный сильный разрыв, перемещающийся вправо (рис. 1). Для наглядности здесь и далее на подобных рисунках будем использовать Лагранжевы координаты, в которых частицы не перемещаются, а, следовательно, траектории границ интервалов являются вертикальными линиями. Точка i является фронтом ударной волны и принадлежит сетке особенностей. Пусть за время т разрыв переходит с n на (n + 1) слой, при этом остается внутри интервала и не взаимодействует с другими разрывами и контактными границами.

Особый интервал состоит из двух интервалов: интервал перед фронтом - « а -интервал», интервал за фронтом « Р -интервал». Для величин на разрыве используются обозначения: «-» - перед фронтом, «+» - за фронтом.

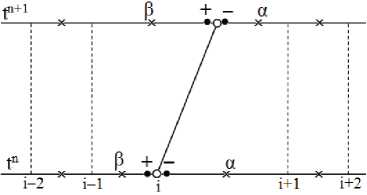
Рис. 1. Шаблон расчета особого интервала

Перед началом расчета интервала с разрывом известны все величины в регулярных интервалах на момент времени t и t^{n +1}. В интервале с разрывом на момент tⁿ известны:

• ( р , E , P , U , C ) - , ( р , E , P , U , C ) + - величины на разрыве;

• •    R D , Wⁿ , Dⁿ - положение и скорости разрыва;

• •    ( р , E , P , M ) ^ - величины в интервале перед фронтом ( а -величины);

• •    ( р , E , P , M ) n - величины в интервале за фронтом (Р -величины).

Здесь р - плотность, Е - удельная внутренняя энергия, Р - давление, U - скорость, С - скорость звука, М - масса интервала, D - скорость перемещения разрыва в Эйлеровых координатах, W - скорость перемещения разрыва в Лагранжевых координатах.

Задача состоит в том, чтобы на момент t^{n +1} определить все величины в интервале с разрывом и величины на разрыве. Алгоритм расчета особого интервала можно разбить на несколько этапов. Не вдаваясь в конкретные операции каждого этапа, рассмотрим общую структуру. Последовательно определяем:

Величины перед фронтом:

• •    новое положение фронта и величины перед разрывом ( р , E , P , U , C ) ^{n + 1};

• •    плотность р О , ^{+ 1} в a-интервале и массу A M , которая «перетекла» сквозь фронт за время т ;

• •    термодинамические величины в ( E , P , M ); n ^{+ 1} а -интервале.

Величины за фронтом

• •    величины за разрывом ( р , E , P , U , C ) ++ ¹;

• •    величины в Р -интервале и его массу М^п р ^{+ 1}.

После проведения данных операций можно говорить, что на момент времени tn+1 в интервале с разрывом определены все величины.

Расчет минус величин n+1                  n+1

I dD I           I dD I

Определим скорость фронта ударной волны D = D + т | — I , где I — I - ускоре- ^ dt )          ^ dt )

ние фронта, полученное с применением дополнительного к условиям Гюгонио уравнения для расчета величин вдоль траектории фронта ударной волны [3]. Новое положение фронта

R D ^{+ 1} = R D + T D^{n + 1}

.

Рассмотрим точку D (рис. 2). Величины в данной точке характеризуют состояние на разрыве перед фронтом в момент t^{n +1} и соответствуют «минус» величинам. Координата точки D совпадает с положением фронта в момент t^{n +1}.

Для нахождения решения в точке D воспользуемся характеристическими свойствами уравнений газовой динамики [1]. Построим характеристический треугольник. Для этого из точки А проведем линию с наклоном как у « характеристики ™Д = ( U + C)A, а из точки В с наклоном как у Р характеристики ДД = (U — C)B " Для

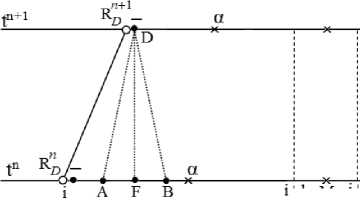
i+1 м 1-2

Рис. 2. Определение «минус» величин

dR точки F построим траекторию   = U^ . Координаты и скорости точек А, Ви F неизвестны и их dt F необходимо определить. Для этого составим систему из трех уравнений. Первое уравнение - это уравнение « характеристики, второе и третье - выражения для U и С, полученные путем линейной интерполяции на n слое. Запишем систему уравнений для точки А

R’ D ^{+ 1} = R A + Т ( U + C ) n ,

UA = U- +

CA = cn +

U n

^RD ⁿ

C n

^RD ⁿ

-

-

n UM n RM

n

-

-

CM

RM

( R A - R D ) ,

( R A - R D ) •

Решив данную систему, получим выражение для определения координаты точки А

R D ^{+ 1}

Ra =---

- Т(U- + C- - R’D (Z 1 + Z2

1 + Т ( Z, + Z 2 )

,

Un где Z1 =

RD

-

-

nn

Um  Z = C - n ,   2 Пп

RM RD

-

-

n CM n RM

•

Для определения R B решим аналогичную систему при этом первое уравнение примет вид r" _d ^{+ 1} = R B + т ( U - C ) B . Получим

R D ^{+ 1} - т (

^RB ⁼

U- - CП - R’D (Z 1 - Z2

1 + Т (Z - Z 2 )

Далее линейной интерполяцией на n слое рассчитываем величины (p, E)AB и из уравнения nn состояния находим РАВ и CA B .

Запишем уравнения, описывающие изменения величин вдоль а и Р характеристик с учетом симметрии ( а = 1, 2, 3)

1      (a -1) UCdt dU ±---dP ± ^--------= 0.

R

p c

Для каждой из характеристик заменим дифференциальное уравнение разностным и после несложных преобразований получим выражения для определения U — ⁺ 1 и P — n ^{+ 1}

Ц П + 1 = ^Ф А - ^Ф B рп + 1 = ^p A C A ^ B - ^p B C B ^ A - P aCa + P B C B ’ "       P aCa + P B C B "

4                      (a - 1) PAUACA.                   (a - 1) PBUBC^

^Здесь Фа = P A ^{+ P} A C A U A                ^T , ^Ф B = P A ^{+ p} B C B^UB                ^T .

RA                               RB

Из точки D опустим на n слой траекторию и найдем положение точки F

R F = R D ^{+ 1} - t U n ^{+ 1}.

Величины (р,E,P, C)F определяются аналогично точкам А и В. Вдоль траектории энтропия по- dP стоянна, следовательно C = —j—. Для определения плотности перед фронтом запишем разност ный аналог этого уравнения

p n ⁺ 1

= pF +

I П +1 _— р

² C_F

Для определения E—+1 проинтегрируем с заданной точностью уравнение изэнтропы dE = — PdV вдоль траектории частицы в пределах (VF, V—+1). Из уравнения состояния найдем давление P—n+1 и скорость звука Cn+1. Таким образом, определено состояние перед фронтом на момент tn+1.

В целях повышения точности проведем пересчет. Для этого из точки D «опустим» характеристики и определим R A , R B следующим образом

R A = R D ^{+ 1} — t ( U + C ) ^{n + 1}, R B = R D ^{+ 1} — t ( U — C ) ^{n + 1}.

Затем пересчитаем «минус» величины для данных координат.

Расчет плотности в a-интервале и массы, перешедшей через фронт

Для учета изменения плотности в a-интервале за шаг по времени представим, что на левой границе интервала ( R D , R D _{+ 1} ) с массой M ^ n отсутствует разрыв, т.е. он является регулярным, его масса не меняется, левая граница движется со скоростью вещества перед фронтом (рис. 3). Обозначим состояние данного интервала на момент tn ⁺¹ индексом С.

Координата левой границы R DC = R D + t UD C ¹, где a dU Л ^{n + 1}

U D c¹ = Uⁿ + t II . Правая граница совпадает с гра-

^ dt у— ницей соседнего регулярного интервала. На момент вре- n+1

мени t n+1 n +1 (RAC , RBC ) ’

определим объем и плотность >C ^{+ 1}, P C ^{+ 1} = md/ o c ^{+ 1}.

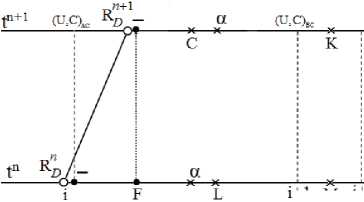
. Тогда плотность в а-интервале на мо- i+1 М 1+2

Рис. 3. Расчет «альфа» величин

Пусть интервал К характеризует ближайший к разрыву регулярный интервал перед фронтом на момент tn+1 мент времени tn+1 определим линейной интерполяцией n+1     n+1      n+1     n +1

Pa = P c ⁺ ( P k ^— P c )

п + 1

RD

^^^^^^^.

Р п + 1

R AC

n + 1        n + 1       n + 1 .

^{2 R}K ^— ( R BC ⁺ R AC )

Далее определим объем а-интервала (RDD1, RBC) ^ 9D+1, его массу M,n+1 = P^Oa+1 и массу, пе- решедшую за время т сквозь фронт ударной волны AM = M n—M'n+1

.

Расчет величин в а-интервале

Предположим теперь, что интервал (RF,Rin+1) является регулярным (см. рис. 3). Точка L -середина интервала. Линейной интерполяцией рассчитываем значения термодинамических величин в этом интервале на момент времени tn+1. На момент времени tn+1 состояние в данном интервале соответствует значениям величин в a-интервале. Таким образом, задача определения альфа величин сводится к расчету регулярного интервала (RF, Rin+1) на момент времени tn+1. Знак вели чины AU = U-+1 - WBD определяет сжатие или растяжение в интервале. Пользуясь методом расчета регулярных интервалов [3], определяем величины в интервале перед фронтом ударной волны. Таким образом, при расчете регулярных интервалов и интервала перед фронтом используется один метод, что позволяет получить одинаковый порядок аппроксимации.

Расчет плюс величин

На фронте ударной волны значения кинематических и термодинамических величин справа и слева в идеальной среде связаны между собой условиями Гюгонио

W (U+- U-)-(P+- P_) = 0, W (V+- V—) + ( U+ - U-) = 0, (E+- E-) + 0,5 (P++ P_)(V+- V_) = 0.

Величина скорости фронта ударной волны Dn+1 и состояние перед фронтом на момент вре мени tn+1 определены. Найдем значение Wn+1

W n ^{+ 1}

= p - ^{+ 1}

( D n ^{+ 1}

- U n ^{+ 1} ) .

Тогда условия Гюгонио в совокупности с уравнением состояния P = P ( V , E ) содержат четыре уравнения и четыре неизвестных. Разрешая полученную систему уравнений, определим параметры на фронте ударной волны в момент времени tn ⁺¹.

Расчет величин в р-интервале

Положение правой границы Р -интервала соответствует положению сильного разрыва. Левая граница является границей соседнего регулярного интервала (рис. 4). Масса в интервале за фронтом равна сумме массы на момент времени tⁿ и массы, перешедшей через фронт ударной волны за шаг т : М ^ ^{+ 1} = М в +A M . Рассчитаем объем ( R in Y, R D ^{+ 1} ) ^ 0ⁿ n ^{+ 1}   и определим плотность

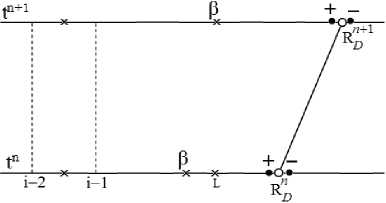
Рис. 4. Расчет величин в интервале за фронтом

n + 1        n + 1 n + 1

p p = ^M p I⁹ P .

Для определения величин в интервале за фронтом поступим аналогично определению величин в a-интервале. Представим, что интервал (Rin+1, RD+1) регулярный, т.е. разрыв на правой границе отсутствует. Определим состояние в данном интервале на момент времени tn. Из точки с координатой RD+1 = 0,5 (RDD + RD+1), «опустим» со скоростью U"p+1 = 0,5 (Uin+1 + U++1) траекто- рию на n слой и получим точку L: RL = R^+1 - tUD+1. Зная распределение величин за фронтом на момент tn, рассчитаем величины в точке L. Теперь Р-интервал на момент времени tn+1 можно рассчитать как регулярный. Заметим, что подобные операции проводятся потому, что масса Р-интервала за шаг по времени изменилась, а, следовательно, середина Р-интервала на моменты времени tn и tn+1 не принадлежат одной траектории. По этой причине нельзя использовать Лагранжев метод напрямую.

После определения величин в интервале за фронтом можно говорить, что особый интервал на момент времени t^{n +1} рассчитан полностью.

Особый случай расчета величин в р-интервале

В процессе счета сетка особенностей перемещается относительно регулярной сетки. При этом возникают ситуации, когда разрыв переходит через границу регулярного интервала. В таком случае на момент tn масса в интервале за фронтом равна нулю, т.е. М в = 0 (рис. 5) и применение подхода, описанного выше, приведет к тому, что точка L будет лежать на траектории фронта ударной волны. На практике это приводит к тому, что в профиле величин за фронтом возникают немонотонности. Они являются следствием того, что при расчете Д -интервала некорректно учитываются возмущения, «пришедшие» из области за фронтом. Решить данную проблему можно путем измельчения шага по времени, что негативно отразится на расчете всей системы. В рамках рассматриваемого метода был разработан алгоритм расчета величин в интервале за фронтом при переходе разрыва через границу регулярного интервала.

Временно исключим из рассмотрения регулярную точку ( i -1). Таким образом, эту ситуацию сводим к расчету величин в интервале за фронтом в общем случае. Рассчитаем величины в интервале К, т.е. интервале

( R D ^{+ 1}, R^ ) .

М к = М ? - 1,5

Масса этого

+ А М . Определяем

его плотность

интервала   равна:

объем интервала К и

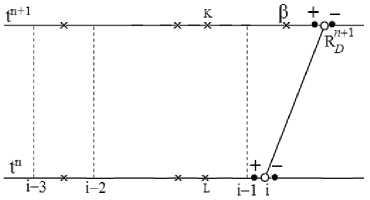
Рис. 5. Расчет р -интервала при выходе разрыва из целой точки

( R in -2 ¹, R D ^{+ 1} ) ^ О к , Р к =

^О к

.

Из точки К опустим траекторию на n слой и находим: RL = Rк - тUK, где

RK = 0,5 (RD+1 + Ri-21), UK = 0,5 (U++1 + Ui-21) . Вт. L найдем термодинамические величины, за- тем, аналогично расчету величин в Д-интервале, описанному выше, определим (Е, P)^

.

На момент времени tn+1 масса в Д-интервале соответствует массе перешедшей через фронт за шаг т: М"р+1 = АМ. Предположим, что в области (RK, RDD+1) распределение плотности и энергии линейные. Найдем такое значение Ri-11, при котором выполнятся условия f . n+1_ АМ

^Р Р      Q ⁿ + 1 ’

I           Ор

Рр+1 = Рк +

n + 1

(Рк - Р++1) Re

RK

^^^^^^^.

RK

^^^^^^^.

n n +1

RD

Для этого итерационно вычислим ноль функции fU”+1) = ^М

\ i ^{- 1}          n + 1

^О Р

^^^^^^^в

Р к

^^^^^^^в

n + 1 n +1 \ R e ^{( Р} к ^{- Р} + ) —

RK

^^^^^^^в

RK

^^^^^^^в

n + 1 . R_D

Определив R i - 11 , рассчитаем U n + 1

и Г —1 ■ ^{+ 1}

dt

n + 1

n + 1    R i - 1

U i - 1 ⁼

^^^^^^^в

v i -1

n             ^{n +} 1        n + 1

R D  ( ^dU |    _ Ui - 1

^^^^^^^в

U +

т

,

dt

i - 1

т

.

Энергию вычислим линейной интерполяцией на (n+1) слое между «плюс» величинами и величинами в точке К

E p ^{+ 1} = Е к + ( Е к - E + ^{+ 1}

n + 1 ) R e R K

^^^^^^^в

RK

^^^^^^^в

n n +1

RD

Давление определяется из уравнения состояния.

Применение данного подхода позволяет корректно учитывать возмущения, догоняющие фронт, тем самым, повысить точность и монотонность профилей величин за фронтом.

Тестовые расчеты

Задача о движении поршня с постоянным давлением на границе по линейному профилю плотности.

Задана область 0 <  R <  1. На левой границе давление PL = 1,5, на правой границе и в области U = 0. Количество расчетных точек равно 10. В области: энергия Е = 0, распределение плотности р ( R ) = 1,7 - 1,4 R . Вещество - идеальный газ, у = 5/3. Симметрия плоская.

На левой границе системы после распада разрыва образуется ударная волна, которая распространяется вправо. На рис. 6 представлено распределение плотности в системе на момент времени t = 0,49, полученное с использованием модифицированного метода. До прихода ударной волны профиль плотности перед фронтом не меняется, т.к. давление в области равно нулю. За фронтом наблюдаем сжатие вещества.

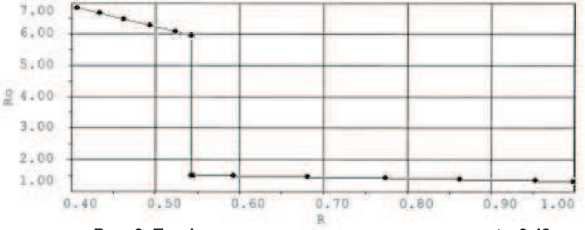
Рис. 6. Профиль плотности на момент времени t = 0,49

На рис. 7 представлены зависимости плотности р _ перед фронтом ударной волны от времени, полученные с помощью метода [3] и модифицированного метода, а также аналитическое решение (начальное распределение).

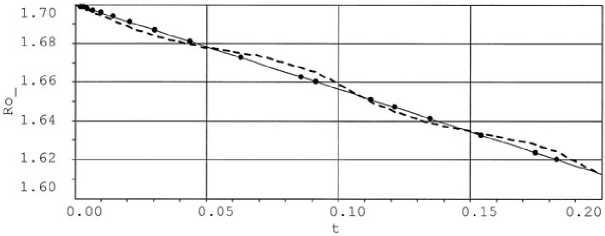
Рис. 7. Зависимости плотности перед фронтом от времени.

Метод [3] (—), модифицированный метод (—), точное решение (•)

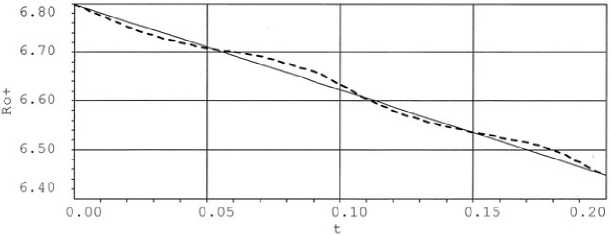
Рис. 8. Зависимости плотности за фронтом от времени.

Метод [3] (—), модифицированный метод (—)

Из рис. 7 видно, что использование метода, основанного на применении уравнений в характеристической форме для определения величин перед разрывом, позволило повысить монотонность и точность расчета термодинамических величин и скорости. Все неточности, возникающие при определении состояния перед фронтом, переносятся сквозь фронт и отражаются на величинах за фронтом, что видно из рис. 8.

Задача о движении поршня с переменной скоростью по постоянному фону.

Задана область 0 <  R <  1. На правой границе и в области U = 0, на левой границе скорость изменяется со временем по закону U L ( t ) = 1 - 1 ² . Количество расчетных точек равно 10. В области: энергия Е = 0,5, плотность р = 1,7. Вещество - идеальный газ, у = 5/3. Симметрия плоская.

От левой границы в систему пойдет ударная волна, за фронтом которой вещество разгружается. На рис. 9 представлено распределение давления в системе на момент времени t = 0,2557.

0.00        0.20        0.40        0.60        0.80     1.00

Рис. 9. Распределение давления в системе на момент времени t = 0,2557

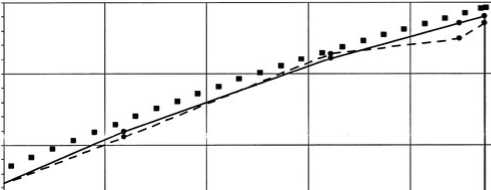
3.20________

0.33        0.35        0.37        0.39        0.41     0.43

Рис. 10. Распределение давления в области за фронтом на момент времени t = 0,2557.

Метод [3] (-•-), модифицированный метод (—), «точное» решение (•)

На рис. 10 представлено распределение давления в области за фронтом на момент времени t = 0,2557. Этот момент времени соответствует моменту перехода разрыва через границу регулярного интервала. Здесь под «точным» решением подразумевается решение, полученное на 1000 точках. Дальнейшее увеличение числа точек при рассмотрении в данном масштабе бессмысленно. Из рис. 10 видно, что профили величин за фронтом ударной волны, полученные модифицированным методом, более монотонные, значения величин на ударной волне ближе к «точному» решению.

Заключение

Предлагаемые способы модификации метода [3] повысили точность и монотонность расчета выделенных ударных волн. Идеология и порядок расчета величин остались прежними, изменились методы их определения. Авторами показана принципиальная возможность использования элементов метода характеристик внутри разностного метода. Данный подход применительно к методу [3] показал свою работоспособность и эффективность. Для любого другого разностного метода элементы метода характеристик можно использовать в качестве интерполяции для определения величин в любой точке пространства и времени. Преимуществом такой интерполяции является учет особенностей уравнения состояния и изменения течения во времени.