О статистической устойчивости оптимального решения, найденного по уравнению регрессии

Поиск оптимальных условий функционирования какой-либо системы является одной из наиболее распространенных научно-технических задач. Она возникает в тот момент, когда установлена возможность проведения проектируемого процесса и необходимо найти наилучшие в некотором смысле условия его реализации. При поиске оптимальных условий протекания процессов пищевой технологии важное место отводится экспериментам и математическим методам их обработки, в частности, регрессионному анализу и планированию экспериментов [1-21].

Поскольку любые экспериментальные исследования, в частности в пищевых технологиях, неизбежно сопряжены с погрешностями, вызванными неточностью измерений и влиянием неконтролируемых факторов, то важным и ответственным моментом при проведении и использовании результатов любых экспериментов является установление точности полученных решений. Это особенно важно при поиске оптимальных условий, т. к. оптимизационные задачи обладают плохой обусловленностью [22, 23] и весьма чувствительны к погрешностям измерений и вычислений.

Как известно [24], в статистических исследованиях для анализа точности и надежности полученных результатов и выводов используются так называемые интервальные оценки параметров случайных величин. Они указывают, в каких границах заключено точное значение параметра исследуемой случайной величины. Настоящая работа посвящена исследованию чувствительности статистических оптимизационных моделей, применяемых в изучении процессов пищевых технологий и разработке методики построения интервальных оценок для численного представления качества результатов оптимизации.

Материалы и методы

Рассмотрим пример оптимизации.

Пример 1. Работа [5] посвящена разработке оптимальной рецептуры комбинированной пищевой системы, т. е. мясного фарша с добавлением растительных ингредиентов. В частности, в ходе проведенных экспериментов была установлена связь массовой доли льняной муки ( X, %) и влагосвязывающей способности ( Y, %) комбинированного фарша. Согласно приведенным данным [5], квадратичное уравнение такой связи для ортогонализированной независимой переменной имеет вид

Y = 75.8333 + 1.8 ( X - 12.5 ) -- 0.06143 [ ( X - 12.5 ) 2 - 72.9167 ] .

Уравнение (1) имеет хорошие статистические характеристики: коэффициент детерминации R ² = 0.968, расчетное значение критерия Фишера для оценки значимости регрессии F_{Bbi ч} = 91.6 при критическом ^ _ритич = 9.55 , остаточная дисперсия s 2 _стат = 16.43 .

Согласно данному уравнению, наибольшая влагосвязывающая способность достигается при X " = 1.8/2 • 0.06143 + 12.5 = 27.15% .

Оценим степень влияния экспериментальных ошибок, допущенных при построении уравнения регрессии на точность определения координаты точки оптимума.

Пусть имеем квадратичное уравнение парной регрессии для ортогонализированной независимой переменной

Y = b + b ( X - X ) - b ( X - X ) ² - A

где x =—Yx — среднее арифметическое экс-N Y i периментальных значений независимой переменной X; A - коэффициент, полученный в процессе ортогонализации Грама-Шмидта.

Тогда оптимальное значение X определяется по формуле xopt = X - bX             (3)

2 b

Как известно, при нормальном распределении экспериментальных ошибок МНК-оценки коэффициентов уравнения регрессии представляют собой случайные нормально распределенные величины, причем при использовании ортогонального плана эксперимента они независимы. Таким образом, координата оптимальной точки квадратичной функции регрессии вида (2), представляет собой случайную величину вида ф = С + ^              (4)

П где % и п—независимые нормально распределенные случайные величины, C - известная константа.

В литературе не были найдены данные о распределении случайной величины (4), поэтому авторы получили соответствующий результат самостоятельно.

Пусть ^ и п — независимые нормально распределенные случайные величины с параметрами ( m 1 , s 1 ) и ( m ₂, s ₂), соответственно. Построим функцию распределения F ( t ) случайной величины (4). По определению функции распределения, значение F ( t ) равно вероятности P ( ф <  t ) того, что случайная величина ф меньше неслучайного числа t , т. е.

P | С + ^ <  t |

I п /

Неравенство в скобках при фиксированном t эквивалентно следующим соотношениям: £           П л

----< п при---- > 0 t - С        t - С

> п при п <  0         (5)

t - С        t - С

— <  0 при t = С п

Обозначим, а F 1 ( x ), f 1 ( x ) – соответственно функцию и плотность распределения случайной величины ^ , а F 2 ( x ), f 2 ( x ) - соответственно функцию и плотность распределения случайной величины п . Тогда в соответствии с (5) функция распределения F ( t ) определится по формуле

'1 - р ( t ) при t - С >  0

F ( t ) = <  P ₂ ( t ) при t - С <  0

где

x оо      и  t-С

P ⁽ t ) = J f l⁽ x ) J ^f >⁽ У ddx + J ^f( x ) J ^f >⁽ y ) dydx

-и      _x_                о0

t - С

x о      Cc             и

^P 2⁽ t ) = J ^f 1⁽ x ) J ^f >⁽ У ) dydx + J ^f ) J ^f , ( y)dydx

-и        о                 о t - С

о       и                и рз = J f.(x )J f2( y dydx + J flI x) J f>( y)dydx

-и       о                о

Поскольку

b

J f2( y)dy = F2( b)- F2( a)

a то формулы (7) можно упростить, понизив кратность интегралов:

_ Р3 при t = С о       (

P 1 (t ) = J f l ( x )к(о) - F 2

-и       \

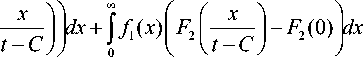
о

P 2 ( t ) = J f l ( X ) I F 2

-и

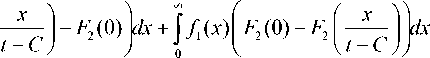
P ₃ = F (о) • ( 1 - F 2 (о) ) + ( 1 - F l (о) ) • F 2 (о)

Вычисления по формулам (6), (8) несложно выполнить с использованием системы компьютерной математики МаthСАD с учетом того, что для нормального распределения в системе существуют встроенные функции pnorm dnorm для F j ( x ) и f j ( x ), i = 1, 2, соответственно.

На основании формул (6), (8) найдем выражение для плотности распределения f ( t ) = F '( t ) , воспользовавшись правилом дифференцирования под знаком интеграла:

Для проверки адекватности полученной плотности воспользуемся имитационной моделью. Для повышения надежности результата вместо обычных псевдослучайных чисел применим ЛП т -последовательность И.М. Соболя [25]. На рисунке 1 приведен совместный график плотности (10) и гистограммы, полученной по результатам имитации случайной величины (4) с помощью 1023 чисел Соболя.

и f (t) = J f4x) f2

-и

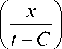
xdx

( t - С )²

Упростим выражение (9), выделив в подынтегральном выражении множитель, зависящий только от переменной интегрирования x и вычислив в явном виде интеграл. Получим

T f ( t ) = '■ n V

D v .пЛ

• exp

T +

D² 2Vs 2 s ₂2

• erf\

где

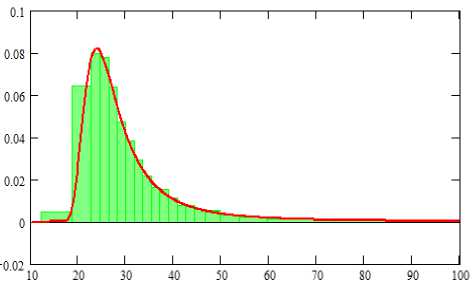
Рисунок 1. Результаты имитационной проверки адекватности плотности вероятностей (10)

Figure 1. Results of simulation verification of probability density adequacy (10)

v=(t - c )2 s2’ + s2,

D = m^s 2 ( t - С ) + m₂s 2 ² ,

- D s,s2 2Vy

T =

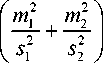
/^ и erf (x) = —;= J e ~ t dt -V п о

встроенная функция системы МаthСАD.

Расчетное значение критерия Пирсона составите 7 _в ² _ьн = 1,З^о4 при х ^ич (о,95) = 3о,144 .

Бугаев Ю.В. и др. Вестник ВГУИТ, 2024, Т. 86, №. 2, С. 48-55 Результаты и обсуждение

На основе формул (6), (8) можно определить область возможного положения оптимальной точки одномерной регрессии при рассеянии, вызванном экспериментальными ошибками. Обозначим

К = b 1 , n = 2 b 2 , С = X (11)

Согласно известной теореме Гаусса– Маркова, величины МНК-оценок b 1 и b 2 распределены нормально с параметрами ( в , ^ K i ) и ( в , ^ д/ K 2 ) , соответственно. Здесь в / — истинные значения коэффициентов квадратичного уравнения регрессии, ст ² - дисперсия ошибок измерения зависимой переменной Y (ошибки экспериментов), K jj – диагональные элементы ковариационной матрицы K коэффициентов функции регрессии (2). Выясним возможную область положения абсциссы X^opt , рассчитанной по формуле (3), если МНК-оценки b j определены согласно (11).

Положим P – доверительная вероятность, с которой необходимо определить искомую область, [ c, d ] – неизвестные границы этой области. Значения c и d будем искать из условия ( d - c ) ^ min при F ( d) - F ( c ) = P . (12)

Воспользуемся данными примера 1. Положим m 1 = P 1 = 1.8, m 2 = 2 P 1 = 0.1229, S 1 = ^[K = Жа К 1 = 0.1938,

s 2 = ^4K2 = V 4 s о2стат K22 = 0.05307, P = 0.9.

Тогда решением задачи (12) будут значения c = 20.492, d = 57.267. Относительно найденной оценки X^opt = 27.15 отклонения от границ возможной ошибки составят -24.5% и +111.9%, соответственно.

Результаты примера 1 показывают, что, несмотря на вполне удовлетворительную значимость полученной регрессии, возможная погрешность в определении положения оптимальной точки весьма велика. Выясним, какие меры следует предпринять, чтобы уменьшить величину погрешности.

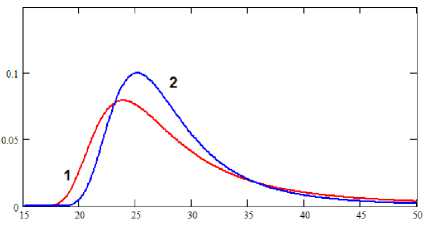
Рисунок 2. Влияние на форму кривой (10) уменьшение дисперсий s ² .

Figure 2. Influence on the shape of the curve (10) reduction of variances s ² .

Очевидно, для этого надо уменьшить ширину пика плотности f ( t ). Несложно убедиться, что для этого достаточно уменьшить значения дисперсий s ² и s ² . На рисунке 2 приведены графики плотностей. У кривой 2 обе дисперсии уменьшены в 2 раза по сравнению с кривой 1. Для того чтобы уменьшить обе дисперсии в n раз можно увеличить число экспериментальных точек тоже примерно в n раз, в частности, провести параллельные опыты. При этом уменьшатся значения диагональных элементов K jj . Однако из графика видно, что уменьшение ширины пика при n = 2 незначительно. Т.е. увеличивая число точек существенно повысить точность проблематично.

Теория планирования эксперимента при поиске оптимальных условий рекомендует решать задачу оптимизации в два этапа. На первом этапе с помощью простых линейных регрессий выходят в область оптимума, а затем строят квадратичную модель в найденной области для уточнения оптимальной точки. Выбор области планирования в окрестности точки экстремума теория объясняет тем, что так называемый коридор ошибок регрессии всегда сужается к центру области планирования, в результате точность модели в центре области максимальна. Однако как при этом меняется стабильность положения экстремума, и меняется ли вообще – неясно. Ответ на данный вопрос позволяют получить построенные нами функции распределения. Продемонстрируем это на данных примера 1.

В примере 1 область планирования – это промежуток [0; 25], немного удаленный от найденной оптимальной точки 27.15. Сымитируем повторную серию экспериментов, используя данные примера 1, но сместим область планирования, взяв в ее качестве отрезок [15; 40], так, чтобы предполагаемая точка оптимума находилась близко к центру области планирования. Для этого в качестве выходных значений Y возьмем значения, полученные в точках новой области по уравнению (1), наложив на них экспериментальные погрешности, совпадающие с полученными в примере 1. Построим по этим синтезированным данным новое уравнение регрессии:

Y = 89.0118 - 0.04285( X - 27.5) -- 0.06143[( X - 27.5)² - 72.9167]

Как видим, при экспериментах в области оптимума значение коэффициента при линейном члене существенно уменьшилось.

Поскольку наложенные погрешности полностью совпадают с допущенными в примере 1, то величина остаточной дисперсии при этом не изменилась 2         , так же как и эле- остат         .     , менты матрицы K. Не изменилась и «кривизна» графика регрессии, т. е. значение коэффициента b1. Значения же параметров m1 и C функции F(t) поменялись: m1 = -0.04285; С = 27.5. Отметим, что при этом уменьшилась оценка числителя дроби (4), а знаменатель не изменился. Это должно привести к уменьшению диапазона величины (4). Действительно, на рисунке 3 приведены графики оригинальной плотности по данным примера 1 и синтезированной плотности после имитации смещения области планирования, второй пик заметно у́же.

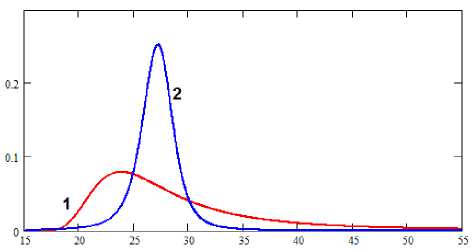
Рисунок 3. Влияние на форму графика плотности (10) смещение области планирования: кривая 1 – исходная плотность, 2 – плотность после смещения

Figure 3. Influence on the shape of the density graph (10) of the displacement of the planning area: curve 1 – initial density, 2 – density after the displacement

Замечание. Оценки значимости регрессии после смещения существенно ухудшились по сравнению с первоначальным вариантом: коэффициент детерминации R2 = 0.643, расчетное значение критерия Фишера для оценки значимости регрессии F = 5.4 при критическом Fкритич = 9.55 . Это произошло потому, что показатели R2 и F вычисляются относительно выч диапазона варьирования экспериментальных значений Y. В области экстремума вариабельность Y значительно меньше, чем вдали от нее. Поэтому для того, чтобы в области экстремума получить значимую регрессию нужно уменьшить экспериментальную погрешность, например, за счет применения параллельных опытов. В результате имитации применения n = 4 параллельных опытов улучшились характеристики регрессии: R2 = 0.878, F = 21.634 , а значения параметров s1 и s2 уменьшатся в  n раз. В результате ширина пика f(t) еще уменьшится. Этот факт изображен на рисунке 4.

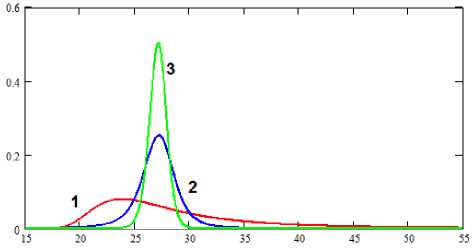
Рисунок 4. Изменения формы графика плотности (10). Кривая 3 – результат применения 4-x параллельных опытов в области экстремума

Figure 4. Changes in the shape of the density graph (10). Curve 3 – the result of applying 4 x parallel experiments in the extremum area

В результате смещения области планирования и применения параллельных опытов 90%-ная область вероятного положения оптимальной точки для примера 1 будет иметь следующие границы [25.744; 28.531]. Т.е. размер доверительной области уменьшится в 13 раз.

Заключение

Часто начальная область планирования экспериментов бывает либо слишком широкой, либо удаленной от оптимальной точки. Поэтому теория планирования эксперимента рекомендует проводить поиск оптимальных значений параметров исследуемого процесса в два этапа. На первом этапе посредством построения линейных регрессий производится локализация области экстремума. Для реализации этого этапа существуют целый набор методов экспериментальной оптимизации: метод Гаусса–Зайделя, метод Бокса–Уилсона, метод симплексов. Первый этап заканчивается, когда применяемые линейные регрессии становятся статистически незначимыми. Если в течение первого этапа требуемая точность не будет достигнута, то реализуется второй этап, на котором положение искомого экстремума уточняется с помощью квадратичной модели. Проведенные авторами исследования подтверждают необходимость указанных двух этапов. При этом получены новые аргументы эффективности их использования и разработаны дополнительные рекомендации при их планировании.

Важным аргументом в пользу необходимости локализации области экстремума и привязки к ней области планирования экспериментов является обнаруженная в ходе исследований возможность существенного повышения статистической устойчивости координат оптимальной точки, найденной по уравнению регрессии.

Бугаев Ю.В. и др. Вестник ВГУИТ, 2024, Т. 86, №. 2, С. 48-55 Полученные формулы для расчета значений функции и плотности распределений положения точки экстремума позволяют оценить размер зоны ее вероятного варьирования.

Было также выяснено, что при построении квадратичного уравнения регрессии в оптимальной области возможно ухудшение показателей значимости регрессии по сравнению с моделями первого этапа. Это может быть вызвано существенным уменьшением диапазона варьирования выходного параметра в стационарной области. Поэтому для построения значимого уравнения регрессии на втором этапе необходимо принять меры для уменьшения влияния экспериментальных ошибок, например, увеличение количества параллельных опытов. Следует отметить, что подобная рекомендация ранее в специальной литературе не встречалась.