О стохастической марковской динамике, приводящей к равновесию Нэша-Вардропа в модели распределения потоков

Ориентированный граф Г = ( V,E ) представляет собой транспортную сеть города ( V – узлы сети (вершины), E С V xV — дуги сети (рёбра графа)). Пусть W = {w = ( i,j ) : i,j Е V} — множество пар источник-сток; p = {у 1 , v 2 , ..., v m } — путь из v 1 в V m , если ( V k ,V k +1 ) Е E , к = 1 , ..., m - 1; P w — множество путей, отвечающих корреспонденции w Е W ; P = U we^ P w — совокупность всех путей в сети Г; x _p — величина потока по пути p , x = {x p : p Е P} ; G _p ( x ) — удельные затраты на проезд по пути p , G ( x ) = {G _p ( x ) : p Е P} ; y e — величина потока по дуге e :

y e = ^2 x p ^ pe , ^где ^ pe = { о e Е p ∈ P

T e ( y e ) — удельные затраты на проезд по дуге e (как правило, возрастающие, выпуклые, гладкие функции), при этом естественно считать, что G p ( x ) = S e _eE T e ( y e ) S pe • Если T e ( y e ) — возрастающие функции, то отображение G ( x ) — строго монотонное. Заметим, что в приложениях часто требуется учитывать и затраты на прохождения вершин графа (в свою очередь эти затраты могут зависеть, вообще говоря, от величин всех потоков, проходящих через каждую рассматриваемую вершину). Пусть также известны потоки корреспонденций d w , w Е W . Тогда вектор x , характеризующий распределение потоков, должен лежать в допустимом множестве:

X = x >  0 : 52 x p = d w ,w Е W

I          peP w

Это множество может иметь и другой вид, если дополнительно учитывать, например, конечность пропускных способностей рёбер (ограничения сверху на y _e ).

Рассмотрим игру, в которой каждому элементу w Е W соответствует свой, достаточно большой ( d w ^ 1), набор однотипных игроков (сидящих на корреспонденции w ). Множеством чистых стратегий каждого такого игрока является P _w ,а выигрыш (потери со знаком минус) определяются формулой -G _p ( x ) (игрок выбирает путь следования p Е P w , при этом он пренебрегает тем, что от его выбора также немного зависят |P _w | компонент вектора x и, следовательно, сам выигрыш -G p ( x )). Тогда, считая отображение G ( x ) непрерывным и строго монотонным (этого достаточно), можно показать, что отыскание (единственного!) равновесия Нэша (1951) x * Е X (макроописание равновесия) равносильно решению задачи дополнительности (принцип Дж. Г. Вардропа (1952)), что в свою очередь равносильно решению вариационного неравенства:

V w Е W,p Е P w ^ x p

( G _p ( x * ) — min G q ( x * )) = q ∈ P w

= 0    ^ V x Е X    G ( x * ) , ( x — x * ) ) >  0 .

Вариационное неравенство можно переписать как проекционное уравнение

x* =Пx (x* — AG(x*)), X> 0, где Пx (x* — AG(x*)) — такая «точка» множества X , которая доставляет минимум функционалу расстояния от точки x Е X до фиксированной точки x* — AG (x*). Выписанное проекционное уравнение можно далее численно решать, например, с помощью метода простой итерации xn+1 = ПX (xn — AG(xn)). Более того, в рассматриваемом случае задача отыскания равновесия Нэша–Вардропа сводится к решению следующей задачи выпуклого программирования [1]:

Е e∈E

p ∈ P x ^p δ ^pe

I

т_Р ( z ) dz ^ min . ^e          x ∈ X

²⁰ Например, шаг с периодом в день можно проинтерпретировать как выбор утром маршрута следования (пути) из дома на работу, исходя из опыта вчерашнего дня. Заметим, что информацию о G p ( x ( n )) водители (игроки) черпают из открытых источников типа Яндекс-пробки, а множитель ( X p ( n ) + 1) определяется исходя из случайного опроса соседей, знакомых, коллег и т.п.

В данной заметке предлагается возможная динамика в этой игре, приводящая к равновесию Нэша-Вардропа. Свой путь на ( n + 1)-м шаге ²⁰ игрок, сидящий на корреспонденции w , выбирает согласно смешанной стратегии (в независимости от всех остальных): с вероятностью

Probp (n + 1) = Yn • (xp (n) + 1) x x exp(-Gp(x(n))/Tn)/Zn, w e W, выбрать путь p e Pw (0 < Yn ^ 1), ас вероятностью 1 — Yn действовать согласно стратегии, использованной на предыдущем n-м шаге. Здесь xp(n) — количество игроков, сидящих на корреспонденции w и выбравших на n-м шаге стратегию p e Pw, а

Z n = ^ Y n • ( X p ( n ) + 1)exp( —G p ( x ( n )) /T n ) .

p ∈ P w

Множитель ( x p ( n ) + 1) характеризует желание имитировать, а также надежность использования этой стратегии. Именно этот множитель подмечает специфику рассматриваемой задачи (без него сходимость будет в общем случае не к равновесию Нэша–Вардропа) и отличает предложенную в статье динамику от многих других (см. ниже краткий обзор). Параметр γ характеризует «консерватизм» («ленивость»), чем меньше γ , тем более консервативный игрок; «температура» T характеризует отношение к риску («горячность»), чем больше температура, тем более «горячий игрок», склонный к более рискованным действиям.

Как показали разнообразные численные эксперименты, часто вполне разумно выбирать Y n ~ 1 /n . При таком выборе Y n наблюдается сходимость при наиболее общих условиях относительно T (вне зависимости от точки старта). Строго говоря, наблюдается сходимость не к равновесию, а к некоторой его окрестности, уменьшающейся с уменьшением T . Стоит обратить внимание на высокую эффективность предложенной процедуры «нащупывания равновесия» с точки зрения количества итераций. Иначе говоря, на предложенный итерационный процесс можно смотреть просто как на эффективный способ численного нахождения равновесия Нэша–Вардропа.

Введение в динамику стохастичности сближает предложенный подход с поиском так называемых «стохастических равновесий в транспортных сетях» [2], с другой стороны, подход данной статьи принципиально от них отличается тем, что предполагает знание транспортных расходов по маршрутам (используется достоверная информация вчерашнего дня), на основе которых производится рандомизированный выбор. В стохастическом же равновесии водитель узнает лишь случайную оценку времени проезда по каждому из маршрутов и затем выбирает маршрут с минимальным временем.

Предложенную схему можно трактовать скорее как стохастическую динамику наилучших ответов в эволюционной (популяционной) игре [3] -- [5], при этом имеется много общего с концепциями quantal response equilibria [6] (используется похожая рандомизация) и minority games [7] (наблюдаются похожие колебания около равновесия). Также близким к предложенному итерационному процессу является концепция генетических алгоритмов [8] и предложенный на их основе эффективный вероятностный (с гиббсовским распределением) алгоритм Григориадиса–Хачияна (1995) [9] поиска ε приближенного равновесия Нэша в матричной игре n x n за O( n • (log ² n ) /е 2 ) операций с плавающей точкой. Стоит заметить, что в классе детерминированных алгоритмов необходимо осуществлять не менее ~ n ² таких операций.

В заключение рассмотрим пример, демонстрирующий, что в результате строительства новой дороги новое равновесие Нэша–Вардропа окажется не эффективным по Парето и будет строго хуже, чем то, которое было до строительства. Тем не менее предложенная выше марковская динамика наилучших ответов приводит именно к такому, не оптимальному по Парето, равновесию.

Пример (парадокс Брайеса, 1968). Пусть корреспонденция x 14 = 6 (тысяч автомобилей / час). Вес ребра (удельные затраты на проезд по этому ребру) есть время движения по ребру (в минутах), если поток через ребро есть y ij (тысяч автомобилей / час). Например, в случае 2: У 24 = x 124 + x 1324 (рис. 1). Естественно считать, что время движения — возрастающая функция потока.

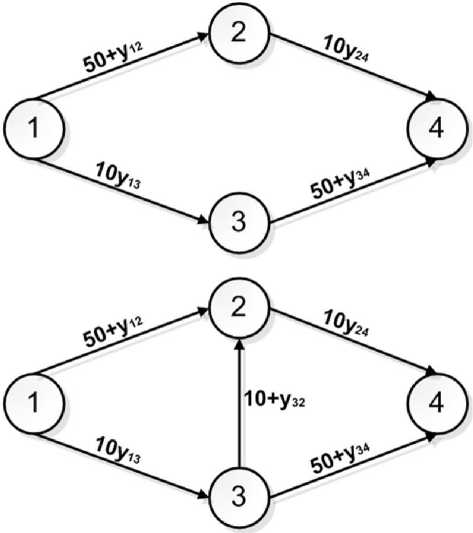
Рис. 1. Случай 1: x 124 = x 1-34 = 3 (полное время в пути T = 83 мин). Случай 2: x 124 = x 1-324 = x 1-34 = 2 (полное время в пути T = 92 мин)

Оба равновесия Нэша–Вардропа (в случае 1 и 2) являются притягивающими положениями равновесия описанной выше динамики (положили Y ~ 1, T ~ 15 — 35), рис. 2, 3 (для случая 2).

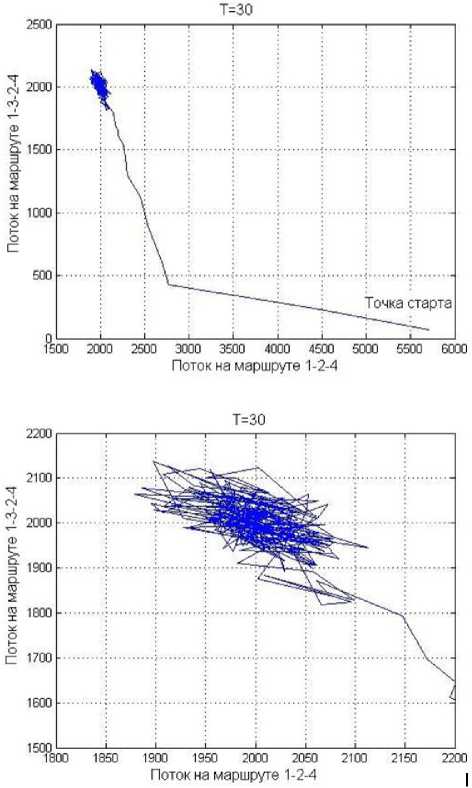
Рис. 2

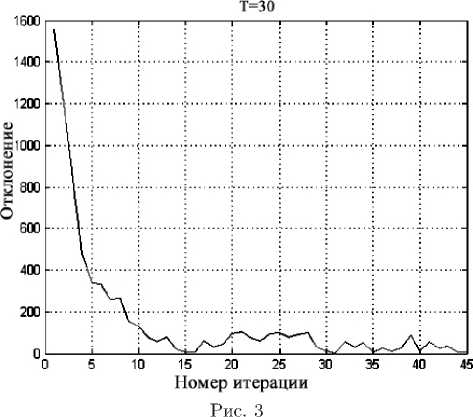
тать, например, в книгах [1, 2, 10]. Значительно более подробные материалы, посвященные эффективным численным методам отыскания равновесий Нэша–Вардропа и решениям задач выпуклого программирования, содержатся в следующих электронных ресурсах [11].

Работа поддержана грантами РФФИ № 10-07-00620-а, 10-01-00321-а, 11-01-00494-а. Работа проведена в рамках реализации ФЦП «Кадры инновационной России» на 2009--2013 годы (меропр. 1.3.1, НК-215П, П1490).