О структурах моделей систем отопления, используемых в алгоритмах регулирования процесса теплоснабжения

Введение. Известно, что задачи погодного регулирования процесса теплоснабжения, в частности, вопросы построения графиков количественнокачественного регулирования отпуска теплоты рассмотрены в достаточно большом количестве работ [1–4 и др.]. Получены существенно значимые и интересные для теории и практики результаты. Применяемые системы автоматизации обычно решают задачу управления процессом посредством компенсации основного возмущения для теплового режима зданий (ТРЗ) – температуры наружного воздуха. Как правило, при этом используются хорошо известные алгоритмы Е.Я. Соколова (см., например, [1]). В работах [4, 5] приведен обоснованный вывод уравнений Е.Я. Соколова для количественно-качественного регулирования систем централизованного теплоснабжения. При этом было установлено, что системы отопления зданий представляются эквивалентным отопительным прибором. Это достаточно принятый и разумный в существующих условиях прием, когда в реальных условиях системы отопления содержат в своем составе отопительные приборы разных типоразмеров и разных сроков эксплуатации и, возможно, с различными вариантами подключения к подводящим и обратным теплопроводам. Очевидно, что прямой анализ режимов работы таких систем является весьма трудной задачей. Целесообразность такого подхода обуславливается еще и тем, что, как это показано в работе [6], параметры эквивалентного отопительного прибора достаточно успешно определяются по экспериментальным данным. В данной работе рассматривается вопрос о рациональной структуре математической модели эквивалентного отопительного прибора, которую следует использовать при разработке алгоритмов регулирования.

Структуры моделей систем отопления. В алгоритмах регулирования Е. Я. Соколова считается, что коэффициент теплопередачи отопительных приборов k зависит от температурного напора A t и с приемлемой точностью может быть определен по следующему уравнению:

k = mAt n , (1) где A t - среднее значение температурного напора отопительного прибора, m и n – некоторые эмпирические коэффициенты. Следует заметить, что A t обычно вычисляют по соотношению:

^{A t} = ^(tBX + t BbIX )/ ² - t B , ⁽²⁾ где t_В – температура внутреннего воздуха, t_ВХ и t_ВЫХ – соответственно температура на входе и выходе отопительного прибора.

Как известно из теории теплообмена, тепловой поток (мощность) W отопительного прибора в этом случае будет равен

W = m A t^{n + 1}F, (3) где F – площадь поверхности отопительного прибора.

С другой стороны, тепловой поток отопительного прибора W можно определить и по следующей формуле:

W = k A tF = k[(t Bx + t BMx )/2 — t B ]F =

= | t BbIX = t BX ^{- W/ (cG}np)| =

= kF[t Bx - t B - W/(2cG np )]. (4)

Следовательно,

W = kF(t Bx - t B )/[1 + kF/(2cG np )]. (5)

В данной формуле GПР – массовый расход теплоносителя через прибор (систему отопления), с – удельная теплоемкость теплоносителя. Заметим, что уравнения (3) и (5) являются двумя различными вариантами модели эквивалентного ото- пительного прибора, которым представляется система отопления.

Для отчетливого понимания последующих выкладок требуются пояснения. Температуру и массовый расход воды из подающей магистрали тепловой сети на абонентский ввод обозначим через tC и GC соответственно, температуру и расход обратной воды на узел смешения через tОБР и GОБР , а температуру и расход теплоносителя после узла смешения, т. е. на входе системы отопления, как tСО и GСО (рис. 1).

t_C , g_C                       t _СО , g_СО

------------►          ------------► tОБР , gОБР

Рис. 1. Расчетная схема узла смешения

Согласно закону сохранения энергии (тепловому балансу) и 1-му закону Кирхгофа, можно записать следующие соотношения:

G CO = G C + ^GОБP ;                        (6)

^сGCО^tCО = ^сGC^tC + ^сGОБP^tОБP .            (7)

В нашем случае вся система отопления здания заменяется эквивалентным отопительным прибором, следовательно, все соотношения, указанные выше, справедливы и в данном случае, однако теперь необходимо учесть, что   tBX = tCO, tBЫХ = tОБP и GnP = GCO. В связи с этим тепловой поток (мощность) системы отопления будет равен

W co = (kF) Co (t Co - t B )/[1 + (kF) Co /(2cG co )] (8)

В формуле (8) (kF)СО – это тот параметр, который подлежит определению посредством решения задачи параметрической идентификации модели системы отопления [6].

При использовании модели (3) выражение для мощности системы отопления будет следующим:

W co = (mF) co At C + 1 ,                      (9)

где (mF)СО – параметр, который тоже следует определять при идентификации модели системы отопления.

Вычисление разности температурных графиков. Согласно работам [4, 5], классический алгоритм управления теплоснабжением по отопительной нагрузке, полученный с использованием модели (9), представляется следующим соотношением:

t c = t B ^{+ A t}Co^{Q 1/(n + 1) + [(t}C ^- ^БР ) ^-

• -0,5(t Co - t O^ j x Q. (10)

Уравнение (10) с точностью до обозначений при n = 0,25 совпадает с уравнением (4.38), приведенным Е.Я. Соколовым на с. 132 в [1].

В этом случае Q = Q/Q ^P = (t_B-t_H)/(t B -t H ) — относительные теплопотери здания, а параметры расчетного режима обозначены верхним индексом «р».

Необходимо также отметить следующее: как это было установлено в [6], значимой практической необходимости в учете зависимости коэффициента теплопередачи k от температурного напора A t нет. В работе [6] показано, что пересчет найденных по экспериментальным данным параметров (mF)_СО и n модели (9) в параметр (kF)_СО дает практически те же самые значения, что и для случая, когда сам параметр (kF) _СО при решении задачи параметрической идентификации непосредственно оценивался по тем же экспериментальным данным. Поэтому при выводе алгоритма регулирования допустимо считать, что (kF)_C0 = (k ^P F)_C0 . Это позволяет заметно упростить конечные соотношения. Кроме того отметим и следующие обстоятельства. Известные в литературе попытки повысить точность расчетов за счет более глубокого учета механизма явлений оказались малоэффективными, так как погрешности расчетов определяются в основном погрешностями исходных данных, которые, к сожалению, довольно высокие. Здесь, к примеру заметим, что, как это хорошо известно, весьма проблемной характеристикой в теплопередаче является коэффициент теплоотдачи; этот коэффициент трудно определяется, поэтому появилась идея построения так называемой новой теории теплопередачи, в которой этот коэффициент просто не используется [7]. По всем этим причинам погрешность теплотехнических расчетов может достигать 30 и более процентов. Поэтому наиболее целесообразно из всех возможных вариантов модели теплопередачи использовать самую простую по структуре, но при этом достаточно проверенную на практике модель.

В самом деле, если же считать, что (kF)C0 = (kPF)C0, то получим, что уравнение регулирования процесса теплоснабжения будет иметь вид tC = tB + AtCoQ + [(tC - tОБP ) -

• -0,5(t Co - t Osp )] x Q. (11)

Как видно из (11), показателя n в алгоритме уже нет, т. е. соотношение упростилось. При этом, как это выяснилось в процессе решения задачи, для получения формулы (11) нет прямой необходимости в том, чтобы специально пересмотреть процедуру вывода [4, 5], оказалось, что всего лишь

Инженерное оборудование зданий и сооружений

достаточно в алгоритме (10) просто формально положить n = 0 .

Для полноты исследования следует оценить разность между температурными графиками (10) и (11) - A t e , Для этого из уравнения (10) вычтем уравнение (11), тогда будем иметь

At e =At Co -[Q^ n ^{+ 1)} -Q]. (12)

На рис. 2 приведены кривые, показывающие, как изменяется A t e в зависимости от относительной тепловой нагрузки Q при n = 0,25 : кривая 1 для Δt_С ^Р _О = 64,5 °С (температурный график 95/70 °С ), а кривая 2 для Δt ^Р _СО = 69,5 °С (температурный график 105/70 ° С).

Как следует из рис. 2, наибольшее различие температурных графиков не превышает 5,7 °С (кривая 2), что на практике малозначимо при реальной точности поддержания температурных графиков.

Зависимость (12) имеет максимум при Q = (n + 1)-(n+1)/n , этот максимум равен AteMAx = Ateo -[(n + 1) -1/n - (n + 1)-(n+1)/n]. В частности, при n = 0, 25 относительная тепловая на- грузка, при которой достигается максимум различия температурных графиков, будет равна Q=1,25-5 = 0,327, при этом AteMAX = 0,0819 -AtC0 .

Среднее значение разности температурных графиков, очевидно, будет равно

Ate = j A t Co -[ Q^{1/(n + 1)} - Q ] dQ =

= ^{A t}eo ■

n + 1 1 — n + 2 2

что, например, для температурного графика 105/70 ° С при n = 0,25 составит всего 3,86 ° С .

В то же время следует отметить, что, как это было указанно выше, на практике фактическая точность поддержания температурных графиков теплоснабжения, к сожалению, не велика, погрешность может быть 20 °С и более. На рис. 3 приведены кривые фактической и расчетной (по графику) температуры теплоносителя в подающей магистрали тепловой сети, а также и соответствующая им кривая температуры наружного воздуха за один календарный год [8].

На рис. 3 кривые 1 и 2 – соответственно расчётная и фактическая температура теплоносителя

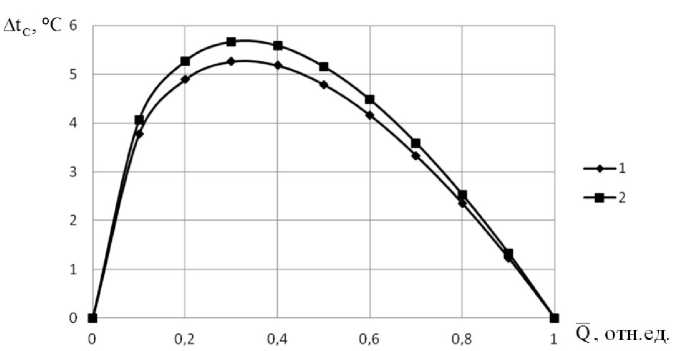
Рис. 2. Различие температурных графиков

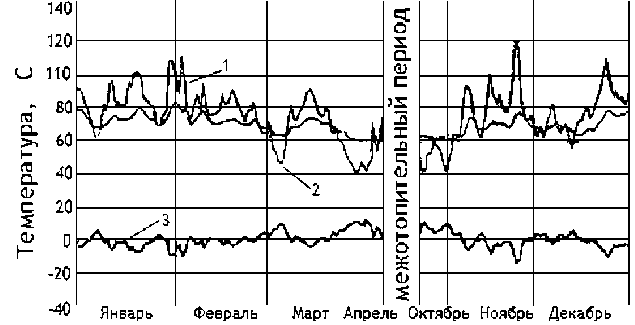
Рис. 3. Графики изменения температуры

в подающем теплопроводе системы теплоснабжения; кривая 3 – температура наружного воздуха.

Следует отметить, что в работах [9, 10] рассмотрены два варианта математической модели отопительного прибора: первый вариант – это формула (5), а второй вариант модели точнее учитывает физику явлений в приборе, поэтому он сложнее и получен на основе классической теории теплообменников. В [9, 10] показано, что в практически интересных случаях расхождение мощностей отопительных приборов, вычисленных по указанным вариантам моделей, весьма незначительно. Следовательно, и с этой точки зрения предпочтительнее использовать модель (5), как более простую по структуре.

Выводы. В работе аргументированно показано, что при разработке алгоритмов регулирования процесса теплоснабжения нет практической необходимости в учете зависимости коэффициента теплопередачи эквивалентного отопительного прибора от температурного напора. Разность температурных графиков теплоснабжения, построенных как с учетом отмеченной зависимости, так и без ее учета, получается практически малозначимой.