О структуре окрестности гомоклинической траектории к негрубой неподвижной точке

В теории бифуркаций особое место занимают задачи, связанные с изучением глобальных бифуркаций многомерных систем с гомоклиническими траекториями к негиперболическим состояниям равновесия или периодическим движениям [1]. Такие системы характеризуются неравномерно гиперболическим поведением траекторий, и они являются пограничными между грубыми гиперболическими системами и системами со сложным

• ^#    Работа выполнена при финансовой поддержке Российского научного фонда, грант № 24-11-00339. (0 2025 Гордеева О. В., Гордеев В. Е.

хаотическим поведением траекторий, для которых характерно существование гомоклинических касаний и всех тех непредсказуемых динамических явлений и бифуркаций, которые они привносят [2, 3].

Основные элементы теории глобальных бифуркаций систем с гомоклиническими орбитами к негиперболическим периодическим траекториям были заложены в работах В. С. Афраймовича и Л. П. Шильникова [4–6]. С точки зрения нелинейной динамики, в этих работах были заложены основы теории такого часто наблюдаемого в приложениях типа странных аттракторов, которые называются «тор-хаосом». Такой тип хаоса возникает при разрушении резонансного двумерного инвариантного тора после того, как существующие на нем устойчивое и седловое периодические движения сливаются в седло-узловое и исчезают. Подробно этот механизм возникновения тор-хаоса, который называется также переходом к хаосу через разрушение двумерного тора, представлен в работе [6], см. также [7].

Одним из основных случаев разрушения инвариантного тора, указанным еще в [4], является случай, когда в критический момент седло-узловое периодическое движение имеет еще и трансверсальную гомоклиническую траекторию. Основные результаты, связанные с исследованием возникающих здесь глобальных бифуркаций, были получены в работе Лукьянова и Шильникова [8].

Напомним, что в работе [8] рассматривалось однопараметрическое семейство F µ многомерных C ^r -гладких диффеоморфизмов ¹ таких, что

• •    при µ = 0 диффеоморфизм F 0 имеет трансверсальную гомоклиническую траекторию Γ 0 к невырожденной седло-узловой неподвижной точке O;

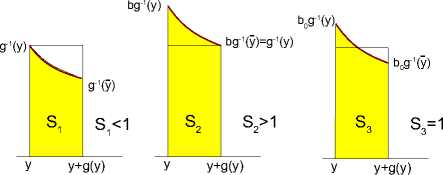
• •    при µ < 0 неподвижная точка исчезает, а при µ > 0 она распадается на две грубые неподвижные точки — седловую O 1 µ и устойчивую O 2 µ , см. рис. 1.

  

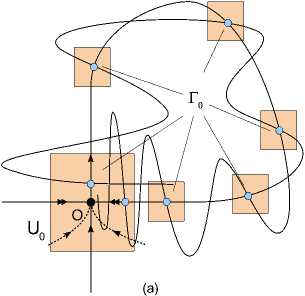
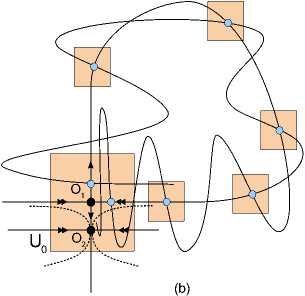
  Рис. 1. Примеры двумерных диффеоморфизмов с трансверсальной гомоклинической траекторией Го к неподвижной точке в следующих случаях: (а) неподвижная точка O является точкой седло-узлового типа; (b) точка O распадается на две, устойчивую O2 и седловую O1, траектория Го(^) становится гомоклинической к точке O1. В каждом из случаев показана также окрестность U гомоклинической траектории, которая состоит из окрестности Uo точки O и конечного числа малых окрестностей тех точек траектории Го, которые не попали в U0 . В случае (b) окрестность U0 содержит обе точки O1 и O2 .

  
  
  
  
  

Основное внимание в работе [8], как и в цикле работ Афраймовича и Шильникова [4–6], было уделено исследованию динамических явлений, происходящих при исчезновении седло-узла (для ^ < 0). Здесь была получена серия замечательных результатов, которые составили в совокупности основу математической теории известного в нелинейной динамики сценария перехода к хаосу через перемежаемость [9]. Однако в работе [8] был также исследован случай (при ^ ^ 0), когда седло-узел распадается на две неподвижные точки. Тогда гомоклиническая траектория, уже к седловой неподвижной точке O i ^ , сохраняется. При этом, как показано в [8], при достаточно малых ^ сохраняется и нетривиальное гиперболическое множество N µ , которое состоит из всех неблуждающих траекторий (за исключением точки О ^ ^ при ^ > 0), целиком лежащих в достаточно малой фиксированной окрестности U = U(О U Г о ) гомоклинической траектории Г д . Такая окрестность состоит из окрестности U g точки О и некоторого числа окрестностей тех точек траектории Г д , которые не лежат в U g , см. рис. 1.

Для того чтобы сформулировать соответствующий результат из [8], напомним сначала некоторые факты из символической динамики.

Топологической схемой Бернулли из двух символов B 2 называется дискретная динамическая система а : Q ^ Q, определенная на полном метрическом пространстве Q бесконечных в обе стороны последовательностей вида ш = (..., a i , a i +i ,...), где a i = { 0,1 } , i = 0, ± 1,... На Q вводится метрика

РМ = "г к=-ж и оператор а, гомеоморфизм на Q, которых сдвигает каждый символ последовательности на единицу влево: аш = ш‘, ш = {ak}, ш‘ = {вк}, вк-1 = ak. Рассмотрим подмножество Q" С Q, выделяемое следующими условиями:

• 1)    Q " не содержит последовательностей, в которых есть два соседних символа «1»;

• 2)    для любой последовательности из Q ^ , длина любого полного отрезка из символов «0» не меньше, чем k .

Теорема [8] . Существуют такие ^ д > 0 и натуральное к, что при всех 0 С ^ С ^ о динамическая система F ^ \ _N топологически сопряжена с системой а : Q " ^ Q " .

В настоящей работе мы обобщаем этот результат на случай двумерных диффеоморфизмов с трансверсальной гомоклинической траекторией к негрубой неподвижной точке, имеющей произвольное конечное вырождение.

(a)                                       (b)

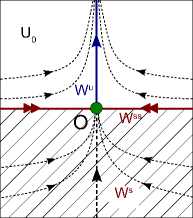
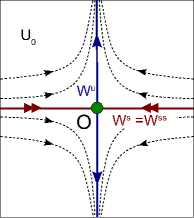
Рис. 2. Структура окрестности неподвижных точек типа (a) седло-узел и (b) сложное седло в случае двумерных отображений.

В работе рассматривается однопараметрическое семейство C ^r -гладких двумерных диффеоморфизмов f µ , удовлетворяющих условиям A)–C):

• A)    При у = 0 диффеоморфизм f o имеет неподвижную точку O с мультипликаторами v i = 1 и V 2 = А, где 0 <  | А | < 1. Предполагается также, что неподвижная точка O имеет вырождение порядка n ^ 1 и ее ляпуновская величина положительна, т. е. при n нечетных это точка типа седло-узел, а при n четных — типа сложное седло.

Заметим, что в этом случае локальное отображение T o , т. е. ограничение диффеоморфизма f на достаточно малую окрестность U o точки O, с помощью некоторой C r^{- 1} -гладкой замены координат может быть приведено к виду [10]

T o : x = Ах(1 + h(x,y)), y = y + y n ⁺¹ + P(y), (1)

где h(0, 0) =0 и P (y) = O(y n + ² ). Из формулы (1) вытекает, см. также [1, 7], что качественная картина поведения траекторий вблизи таких точек будет такой же, как и в невырожденном случае: как у простого седло-узла (при n = 1) и у грубого седла соответственно, см. рис. 2. У неподвижных точек этих двух типов можно выделить два одномерных локальных инвариантных многообразия. Во-первых, это сильно устойчивое многообразие W ss (O) : { y = 0, | x | < е } , и, во-вторых, это неустойчивое многообразие W ^u (O), которое в случае седло-узла имеет уравнение { х = 0, 0 < y < е } , а в случае сложного седла — уравнение { х = 0, | y | < е } .

На рис. 2 показано как такие многообразия устроены локально. Эти локальные многообразия продолжаются до глобальных, которые, как известно, не являются подмногообразиями (например, в топологии плоскости), но мы предполагаем, что они пересекаются таким образом, что

• B)    Инвариантные глобальные неустойчивое W ^u (O) и сильно устойчивое W ss (O) многообразия неподвижной точки O диффеоморфизма f o пересекаются трансверсально в точках некоторой гомоклинической траектории Г о , см. рис. 1a.

• C)    При у >  0 точка O cтановится грубой седловой неподвижной точкой диффеоморфизма f и траектория Г о (у) является грубой (трансверсальной) гомоклинической к ней траекторией.

• 2. О структуре итераций отображений вблизи негрубых неподвижных точек

Основной результат работы — это следующая теорема.

Основная теорема. Пусть f µ — непрерывное однопараметрическое семейство C ^r -гладких, r ^ n+3 , двумерных диффеоморфизмов, удовлетворяющее условиям A)-C). Тогда существует такая достаточно малая фиксированная окрестность U = U(O U Г о ), такие y i >  0 и натуральное k, что при каждом фиксированном у G [0, y i ] ограничение f ^ на множество N µ неблуждающих траекторий из U топологически сопряжено с системой a : Q k ^ Оу При этом N ^ является равномерно гиперболическим множеством при у >  0 и неравномерно гиперболическим при у = 0 .

Оставшаяся часть работы посвящена доказательству этой теоремы. Вo втором параграфе мы доказываем некоторые результаты о структуре итераций одномерного отображения, которое в нашем случае, является ограничением диффеоморфизма f µ на его центральное многообразие. Полученные результаты имеют вполне самостоятельный интерес, они также существенно используются при доказательстве основной теоремы, которое мы даем в третьем параграфе.

Рассмотрим однопараметрическое семейство C r -гладких одномерных отображений вида л : у = (1 + р)у + yn+1 + P(y,^,                        (2)

где р — параметр, P(у,р) = O(y^{n +2} ) и r ^ n + 2. Нас интересует прежде всего поведение траекторий отображения т ^ на полуинтервале I q = [0, е) значений координаты у при достаточно малом фиксированном е >  0, не зависящем от р.

Отметим, что одномерное отображение у = (1 + р)у + y ⁿ⁺¹ + ... является весьма частным случаем общей n-параметрической нормальной формы у = р о + (1 + p i )y +... + р _{п -} 1У^{п —} + y ⁿ⁺¹ +... для бифуркаций одномерных отображений (или многомерных отображений в ограничении на центральное многообразие), имеющих негрубую неподвижную точку с мультипликатором +1. В отличие от общей нормальной формы, в отображении (2) координата неподвижной точки у = 0 при изменении параметра р сохраняется. Кроме того, при р >  0 она становится грубой седловой (что согласуется с условием C)), и на интервале (0, е) с достаточно малым е >  0 других неподвижных точек не появляется.

Таким образом, задача исследования поведения траекторий в однопараметрическом семействе (2) становится интересной с той точки зрения, что ее решение позволит разобраться в тонких вопросах перехода от неравномерно гиперболической к равномерно гиперболической динамике, в том числе при исследовании соответствующих глобальных бифуркаций. В случае коразмерности один, n = 1, такие бифуркации изучались в работе Лукьянова и Шильникова [8], для случая невырожденного седло-узла, соответствующую теорему мы сформулировали во введении. В нашей работе мы обобщаем этот результат Лукьянова и Шильникова из [8] на случай произвольного n.

Для этой цели в настоящем параграфе мы выводим формулы для итераций отображения т(р) и их производных на полуинтервале I q = [0,е) , которые будут справедливы для достаточно малого фиксированного и не зависящего от р значения е >  0.

Докажем сначала общий результат о вложении в поток одномерного отображения в окрестности негрубой неподвижной точки.

Лемма 1. Рассмотрим m-параметрическое семейство C ^r -гладких (г ^ 2) одномерных отображений вида

У = У ⁺ д⁽у^,р),                                     ⁽³⁾

непрерывно зависящих от параметров р, область значений которых Am принадлежит шару ||р|| < $о и содержит точку р = 0. Пусть существует такое eq > 0, что для всех р G Am и всех 0 < у < eq выполняются условия д(0,р) = 0, д'у (0, 0) =0 и д'у(у,р) > 0. Тогда отображение (3) на интервале 0 < у < eq при р G Am совпадает с отображением сдвига на единицу времени по траекториям некоторого Cr-1-гладкого потока у = д(у,р)                                     (4)

и функция д(у, р) определяется на интервале 0 < у <  e q по функции д(у, р) однозначно.

• <1 По определению, отображение (3) вкладывается в поток (4), если выполняется интегральное равенство

y

/ дк^ = ^{1.                           (5)}

y

Это означает, что за t =1 мы переходим вдоль траекторий такого потока из точки у в точку у в соответствии с формулой (3). Теперь наша задача показать, что уравнение (5) имеет решение и оно единственное.

(a)                (b)                         (c)

Рис. 3.

Посмотрим, что будет при g(s,p) = g(s,p). В этом случае, поскольку g(y,р') — возрастающая функция (соответственно, g^-1(y,р') — убывающая), имеем, см. рис. 3a,

—

y t' ds

J g(s,p)

y

—

y t' ds

J g⁽y^{,р) y}

y - y g^y,^)

Пусть теперь g(s,p) = в 1 g(s, р), где мы возьмем такое в >  0, что eg 1 (у) = g 1(у), см. рис. 3b. В этом случае — ^y

Г ds > у - у = 1 J g^, р) g(y, р) ’ y и для β имеет место соотношение в = 9(рр) g(y,р)

₉ ( ^у. ^{р )}(1+ g- ( „ ( ^{у )} .^{р ))} = i ₊ g („(у), р) g(y)

где в (у) — некоторая промежуточная точка на интервале (у, у).

Таким образом, получаем, что существует некоторая функция в = в о (у, р) >  1 такая, что при g(s, р) = в о (у, Р)g(s, р) выполняется соотношение (5).

Покажем теперь, что функция g(y, р) определяется по функции g(y, р) однозначно. Заметим, что точка у = 0 является неподвижной для отображения (3) и состоянием равновесия для потока (4). Это состояние равновесия неустойчиво на интервале у G (0, е) для достаточно малого е >  0, так как Ду = у/ — у = g(y, р) >  0 в силу того, что функция g(y, р) строго возрастающая при у >  0. Отсюда также вытекает, что g y (у, р) >  0 и g(y, р) >  0 при у >  0. Тогда для интеграла (5) на любом интервале [0, е) применима теорема о среднем значении, которая дает следующую формулу.

—

y

!' ds

J g^,^{р) y}

у ^— у = ____________ у ^— у ____________

(№,^{р)   g(}y^,р) + ^eg y ⁽у,^р)(у - у^{) + о(}у ^— у)

_________________ g⁽y^, р) _________________= 1

g(y, р) + „gy (у, р)(у — у) + о(у — у)     , где £ G [y,y], 0 G (0,1) и y G (0, e). Отсюда вытекает, что r g(y,v) 1 lim ——— = 1, y -° g(y,v)

так как y ^ y при y ^ 0.

Докажем теперь, что функция g(y, v) определяется функцией g(y, v) однозначно. Продифференцируем соотношение (5) по y, получим

^{1 +} g'⁽y^{,v)       1}

-

g(y,v)      g(y,v)

n         g(y,v)

= 0 или ——— = 1 + g (y,v). g(y, v)

Предположим, что две функции gi(y, v) и g2(у, V) удовлетворяют этому равенству. Тогда получим, что g1 (y,v) = g2(y,v)

^g 1 ⁽y^{,v)    g} 2 ⁽y^,v) ’

Перепишем эту пропорцию в виде gi(y,v) = gi(y,v) g2 (y,V)    g2(y,V) ’

Заметим, что последнее соотношение выполняется во всех точках траектории отображения (3). В частности, для тех, которые при обратных итерациях сходятся к точке у = 0. Последнее можно записать в следующим образом gAy^ = llm giUti = llm giUti llm g^ti = 1

^g 2 ⁽y^,v)     y ^0 ^g 2 ⁽y^,v)     y -° g⁽y^,v) y -° ^g 2 ⁽y^,v)

Последнее равенство является следствием (6), и оно влечет что g i (y,V) = g 2 (y,V), что и требовалось доказать. >

Замечание 1. Леммы о вложении в поток при v = 0 доказывались в разных работах. В частности, в [11] был рассмотрен случай простого (невырожденного) седло-узла, а в [12] существование гладкого вложения в поток при v = 0 было доказано без предположения о высокой гладкости и о том, что седло-узел простой. См. также § 12.5 из книги [7], в котором представлен ряд результатов на эту тему.

Вернемся теперь к нашему отображению т(v), представленного в виде (2). Очевидно, что оно при v ^ 0 удовлетворяет условиям леммы 1, что позволяет установить некоторые результаты (см. леммы 2 и 3) об итерациях отображения т(v) при всех достаточно малых v ^ 0. В случае v = 0 справедлива следующая лемма.

Лемма 2. При v = 0 для любых yo, yk из Io и любого натурального k таких, что Tk(yo) = yk, выполняется соотношение y =    yk

У 0   nn/1 + nyy^’ где y = Y(yk, k) — некоторый коэффициент, близкий к 1, когда e мало: y ^ 1 при e ^ 0. Кроме того, при фиксированном yk > 0 и больших k справедливы следующие асимптотические оценки:

1      dy o      1

y 0 ∼ √ _{n k}, _{dy k} ∼ _k √ _{n k},

• <1 Рассмотрим отображение у = y + y ⁿ⁺¹ + P(y) где P(y) = O(y ⁿ⁺² ). По лемме 1 оно локально (на интервале I q = [0,е) ) вкладывается в поток ^ q : y = g(y) с g(y) = y ^{n +1} + P(y), где P(y) = O(y ⁿ⁺² ).

Рассмотрим два вспомогательных мажорирующих потока ^ 1 : y = Y i y ^{n +1} и ^ 2 : y = Y 2 y ^{n +1} таких, что

Y i y n ⁺¹ n ⁺¹ + P(y) 2yⁿ⁺¹.

Очевидно, константы Y1 < 1 < Y2 можно выбрать такими, что Yi = Yi(£) ^ 1 при Е ^ 0 и выполняются интегральные неравенства —               —— yyy

1 !' d s        t' d s 1 t' d s

Y2 J sn+1 < J sn+1 + P(s) < Y1 J sn+1 ’ yyy

Таким образом, потоки ^ 1 и ^ 2 при подходящих Y 1 < 1 < Y 2 являются системами сравнения [13] для исходного потока ^ q .

Отображения T 1 и T 2 сдвига за единицу времени вдоль траекторий одномерных потоков y = Y i y ⁿ⁺¹ , i = 1, 2, за единицу времени можно представить в следующем интегральном виде: ^y

T^ : / ^dy₊i = 1,                                     (9)

i J Yi yn+1 y или в явном виде

T i : y=             = y + Y i y ^{n +1} + O ( y ^{n +2} ) .

n 1 - nY i y n

Рассмотрим теперь отображение t q , см. формулу (2) при у = 0. Мы показали, что для его координаты yj справедливы оценки T 1 (y) <  t q (y) < T 2 (y) для всех y G I q . Отсюда следует, что T ^{— 1} (y) < T ^{- 1} (y) <  T ^{— 1} (y). Таким образом, для k-ой итерации отображения t q справедливо неравенство T ^{- k} (y k ) <  т - k (y k ) <  T ^{— k} (y k ).

Пусть yoi и yk такие, что yoi = T-k(yk). Тогда yk

/

dy           1     y k

----=--= k, Yiyn+1      nYiyn y0i y0i откуда получаем, что y„ • =       yk

• ^yQi    J 1 + nY i y n k ,

• и, следовательно, для координаты y o такой, что y o = т - k (y k ), справедлива оценка

yk      < y <      yk      , nJ 1 + nY2ynk       nJ 1 + nY^k из которой сразу следует формула (7). В свою очередь, из нее легко получаются асимптотики (8). ⊲

Рассмотрим теперь отображение τ µ , см. формулу (2), для которого мы докажем следующий результат.

Лемма 3. При всех достаточно малых ц >  0 для любых y o ,y k G I g и любого натурального k таких, что T k (yo') = y k , имеет место соотношение

У 0 =

y _k e - µγk

П1 + (1 - e^^k)ц-1уП ’ где y = Y(ц, Ук,k) — коэффициент такой, что y ^ 1 при ц,£ ^ 0.

<1 Рассмотрим отображения Т^ и Т^^ сдвига вдоль траекторий одномерных потоков ^i ^: У = Y i (цУ + У ^{п +1} ), i = 1, 2, за единицу времени. Заметим, что по лемме 1 отображение т ^ при ц ^ 0 вкладывается в некоторый поток ^ ^ д , для которого оно является отображением за единицу времени. Мы покажем, что для подходящих констант Y 1 и Y 2 потоки ^ ^ 1 и ^ ^ 1 будут являться системами сравнения для потока д ^ д .

Запишем отображение T iµ в интегральном виде

y

dy

Y i (ЦУ + У ^п+1 )

= 1.

Вычислив интеграл

— ^y

/

y

dy

Y i (цУ + У ^п+1 )

=

— y

dy

Y i У ^п+1 (ЦУ ⁿ

+ 1)

=

— ^y

d(цy ⁿ )

- nцY i (цУ ^{- n} + 1)

- ^4 a +4=!

ⁿЦY i \П^п J _v

получим, что

У = —/                    ==.

1 + (e - n^Y - 1)ц ^{- 1} (ц + y ⁿ )

Используя разложение в ряд Тейлора, получим равенство

1 - e-n^i

У = У (^1 + ——-- (ц + y ⁿ )+ O ЦЦ + yⁿ) )j

= y ( 1 + Y i Ц + О ( ц ² )) + Y i ( 1 + О ( ц ) ) у ^{п +1} + О ( у ^{п +2} ) .

Отсюда видно, что наше отображение у = у(1 + ц) + y ⁿ⁺¹ + О ( у ^{п +2} ) мажорируется отображениями Т 1 ^ и Т ₂ ^ с подходящими константами Y 1 < 1 и Y 2 > 1 такими, что Y i ^ 1 при £ ^ 0 и ц ^ 0. Таким образом, для координаты у отображения т ^ получаем неравенство T^y) < т ^ (у) < Т 2 ^ (у). Отсюда следует, что Т -^ у) < T ^{- 1} (y) <  Т ^{— 1} (у). Таким образом, для k-ой итерации отображения т ^ справедливо неравенство Т - k (y k ) < T ^{- k} (y k ) !

Найдем теперь yoi = Т-kyk, вычислив интегральное равенство, yk f dy

J Y i (цУ + У ^п+1 )

-          +     = k

/ y„

Откуда получаем

y o i =

yke-µγik n/1 + (1 - е-п^k)ц-1 yn

Таким образом, справедлива оценка yke-µγ2k

П 1 + (1 - e - nwk )u ^{- 1} y "

< y 0 <

y _k e - µγ 1 k

П 1 + (1 - e n-' k )u ^{- 1} y" ’

из которой сразу получается искомая формула (10). ⊲

Сформулируем теперь следующий результат, который «соединяет» утверждения лемм 2 и 3.

Лемма 4. При любом фиксированном y k ∈ I 0 справедливы следующие асимптотики для y o из (10) :

• 1)    при фиксированном k

lim y ₀ (y k , u, k) =    . У^к   = ~ =;

M ^ +0            / 1 + nYy " k    n k

• 2)    при фиксированном u >  0 и больших k

y 0 ∼ ^{√ n} µe ^-µγk , ^{dy 0} ∼ µ ^{√ n} µe ^-µγk . dy k

<1 1) Формула (12) выводится из условия, что e "^'-k = 1 — nuYk + O(u 2 ) при малых U

• 2)    Асимптотики (13) легко получаются из формулы (10). Действительно, для коэффициента перед e ^-nµγk в (10) получаем

• 3. Доказательство основной теоремы

lim             y k           = y k =      n ^    ,          (14)

k 'x П 1 + (1 — e-n-Yk)u-1 У"   V 1+ u yk   П1+ uy-n что дает искомую асимптотику для y0 при больших k. Дифференцируя последнее выражение из (14) по yk , получаем асимптотику для производной dy0 /dyk при больших k. ⊲

Из лемм 3 и 4 можно вывести тот интересный факт, что поведение траекторий отображения τ µ при больших k и малых µ может меняться от гиперболического, экспоненциального, (когда при u > 0 траектории проходят очень близко к седлу O), см. асимптотику (12), до полиномиального (с порядком разбегания k ^{1 /n} асимптотически меньшее, чем любое экспоненциальное). При этом, в определенные моменты (это будет, когда U = O(k ^{- 1} )) асимптотика должна быть промежуточной — субэкспоненциальной (которая, конечно, присутствует в общей формуле (9), но как ее «извлечь» оттуда, мы не знаем).

Рассмотрим двумерный диффеоморфизм f µ , удовлетворяющий условиям A)–C) из введения. Как показано в работе [10], в этом случае локальное отображение T 0 , т. е. ограничение диффеоморфизма f µ на достаточно малую окрестность U 0 точки O , с помощью некоторой C ^{r- 1} -гладкой замены координат может быть приведено к виду

T o : x = Ax(1 + h(x,y,u)), У = (1 + u)y + y " +1 + P(y,u), (15)

где A = A(u) и 0 <  | A | < 1, h(0, 0,u) = 0, и, в силу условия С), P (y,u) = O(y " + ² )• В этих координатах мы полагаем, что U o { (x,y) : | x | < е, | y | < е } для некоторого достаточно малого е > 0, не зависящего от u.

Везде ниже мы рассматриваем случай, когда д ^ 0. Тогда точка 0(0, 0), которая при д = 0, в силу условия A), является негрубой неподвижной точкой (вырождения порядка n ^ 1) либо типа седло-узлом, либо типа сложное седло, при д > 0 становится гиперболическим седлом (с мультипликаторами А и 1 + д). В координатах (15), многообразие W₍“ имеет уравнение у = 0 и оно делит окрестность U q на две части: U + : {| x | <  е, 0 < у <  е } и U - : {| x | <  е, — е < у <  0 } . Заметим, что траектории в U - не принадлежат N ^ , и поэтому мы их не рассматриваем. Что касается окрестности U + , то траектории, покидающие ее при итерациях f µ , могут возвращаться (даже бесконечное число раз) в силу существования гомоклинической траектории Г о (д). Соответственно, мы будем изучать те траектории диффеоморфизма f ^ , целиком лежащие в U(O U Го).

Что касается локальных свойств диффеоморфизма f µ , т. е. итераций локального отображения T q : U + ^ U + , то для них справедлива следующая лемма.

Лемма 5. Пусть точки M q (x Q ,y Q ) и M k (x k ,y k ) из U + такие, что M k = T k ( M q ) . Тогда существует такое д 1 > 0 , что при всех 0 С д С д 1 выполняются соотношения:

X k = A ^k ^ k (xo,У k ,д),

У 0 = ^ k (y k ,д) = ⁽

y _k e - nµγk

^ 1+(1- e ^{- n}^^Yk ) ^ ^{- 1} у П , y k

^ l+ nYy ^ k ,

д > 0,

Д = 0,

где A = | A | + 5 1 и 5 1 достаточно малая константа (5 1 ^ 0 при е ^ 0) , ^ k (0,y k , д) = 0 , и функция ^ k (x q ,y k , д) равномерно ограниченна по k вместе со всеми своими производными.

Формула (16) для у о получается объединением формул (7) и (10) из лемм 2 и 3, а для координаты x _k она получается стандартно, см., например, [14], прямым итерированием по координате x с учетом того, что последовательность итераций (уо,... ,y k ) по координате y уже известна.

Замечание 2. Формула (16) есть не что иное, как представление отображения T k : U + ^ U + в так называемом перекрестном виде или в (перекрестных) координатах Шильникова. Отметим, что стандартная задача Коши для нахождения траектории (х_о,у о ), (X 1 ,у 1 ),..., (x k ,У k ), где (x i +1 ,y i +1 ) = T q (x i ,y i ), по данным начальной точке (хо,у о ) и k не всегда имеет решение в U q (например, при больших k траектория покидает U q ). Поэтому здесь решается так называемая краевая задача Шильникова [15, 16]: задаются краевые условия x q и y k и число итераций k, по которым находятся x k и у о . Эта задача всегда имеет решение в случае седла. В лемме 5 этот факт устанавливается также и в случае негрубой точки произвольного порядка вырождения для соответствующих решений в окрестности U ⁺ .

По условию C) локальное многообразие W^ : {x = 0, 0 С у < е} продолжается до глобального W“+, которое имеет точки трансверсального пересечения с Wss — это точки траектории Го. Для диффеоморфизма fo, т. е. при д = 0, выберем в Uq две точки M+ (x+, 0) 6 W^ и M-(0, у-) G W^ траектории Го, где x+ > 0, у- > 0. Также выберем достаточно малые окрестности П+ и П- точек M+ и M- соответственно такие, что fo (П± И П±) = 0. Так как M+ and M- принадлежат одной и той же траектории Го, то существует такое натуральное q, что M+ = fq(M-). Тогда в случае диффеоморфизма f при всех достаточно малых д ^ 0 определено отображение T1(д) = f^ : П- ^ Uq, которое будем называть глобальным. В координатах (x, у) на U , отображение T1 можем быть представлено в следующем виде:

x - x + = F (x,y - y , ц) = ax + b(y - y ) + ..., y = G(x,y - y - ,ц) = cx + d(y - y ^- ) + ...,

где, вообще говоря, все коэффициенты зависят от ц, в частности, x ⁺ = х ⁺ (ц) и y - = y - (ц) — это соответствующие координаты двух гомоклинических точек траектории Г ^ . Также имеем, что ad - bc = 0, так как T 1 — диффеоморфизм, и d = 0, так как Г ^ — трансверсальная гомоклиническая траектория. Многоточиями в (17) обозначены члены порядка O(x 2 + (y - y ^- ) ² ).

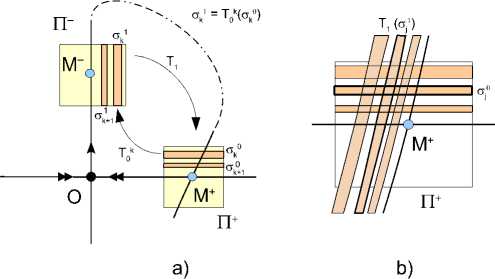
Рис. 4. Иллюстрация геометрических свойств отображений первого возвращения

T i T j : П⁺ -II —— П⁺, областью определения которых является счетное множество полосок a j , j = k,k + 1, ..., на П ⁺ , которые переходят в полоски a j = T ^j (a j ) на II , рис. (a), а затем возвращаются на П ⁺ уже в виде полосок T ₁ (a ¹ ), рис. (b).

Заметим, что каждая траектория из множества N µ по определению должна иметь точки в П ⁺ и П ^- . Более того, точки из П ⁺ , кроме тех которые лежат на W ss , попадают в П ^- под действием итераций локального отображения Т о , а точки из П снова попадают в П ⁺ под действием глобального отображения T 1 и т. д. Таким образом, любой не асимптотической к O траектории из N µ может быть поставлена в соответствие бесконечная в обе стороны последовательность отображений

где T k j = T i T k j : П ⁺ ^ П ^- ^ П ⁺ и jj ^ k для всех j.

Областью определения отображения Tk : П+ ^ П- является полоска ak С П+ такая, что ak = T-k(П-) П П+, см. рис. 4(a) (при этом полоски σk0 с разными k не пересекаются и накапливаются к отрезку Wss П П+ при к ^ от). Соответственно, Tk переводит ak в вертикальную полоску ak С П-, т. е. Tk(a0) = ak (полоски ak не пересекаются между собой и накапливаются к отрезку Wu П П- при к ^ от). В свою очередь, глобальное отображение T1 переводит ak1 в полоску T1 (ak1) на П+ , которая лежит вблизи куска Ti(Wi“c) неустойчивого многообразия точки O и пересекает все полоски ak С П+, рис. 4(b). Такая «седловая» геометрия характерна для всех отображений из последовательности (18). Полоски ak при ц ^ 0, как можно извлечь из оценок леммы 5, при итерациях локального отображения T0 сжимаются по горизонтали и растягиваются по вертикали: для T0k коэффициент сжатия — это величина порядка λk , а коэффициент растяжения варьируется от k1/n при ц = 0 до ц---//1^^ при ц > 0. При этом глобальное отображение T1 , в силу того, что Г0 — трансверсальная гомоклиническая траектория, сохраняет этот порядок растяжений и сжатий, когда точки из П+ снова возвращаются в П+ при итерациях. Это «один в один» напоминает динамику отображений возвращения в случае диффеоморфизмов с подковой Смейла. Это дает возможность применения к этой последовательности леммы Шильникова [14, 15] о седловой неподвижной точке в прямом произведении пространств для того, чтобы доказать, что каждой последовательности вида (18) отвечает ровно одна траектория Л g N (седлового типа), целиком лежащая в окрестности U(O U Го).

Пусть Mj (xj,yj) и Mj(xj,yj'), j =0, ±1,..., — точки траектории Л такие, что Mj g П+ и Mj g П-. Тогда Mj- = Tkj (Mj) и Mj+1 = T1(Mj). Эти соотношения в координатной форме можно записать в виде x0+i -x+ = F(x1,yj -y-^), yj+i = G^yj -y-^), j = 0,±1,...,    (19)

где в силу леммы 5

x ¹ = \ ^{k j} ^ _{k j} (x j ,y j ,p), y ⁰ +₁ = $ _k j (y j +i ,^, j = 0, ± 1,...             (20)

Последовательность (19)–(20) можно теперь переписать в так называемом перекрестном виде. А именно, поскольку Gy(0) = d = 0, здесь используется условие С) трансверсальности гомоклинической траектории Го, второе уравнение из (17) можно разрешить относительно координаты yj — y-. В силу (17) получим yj — y- = dy°j+i — cxj + ...). Используя формулы (20), это соотношение перепишем как yj — y- = Gj jyj+i’p) = d ($kj+1 (yj+i,^)(1 + ...) + ^j^kj (jy^p)^ .

Тогда последовательность (18) можно переписать в таком виде x0+i — x+ = Fj (xj,yj+1,P), yj — y- = Gj (jyj+^P), j = 0, ±1,-..,     (21)

где в силу лемм 2 и 3, а также леммы 5, мы для всех 0 С P < P 1 всегда можем написать такие оценки

( ^{1 /n}

| F j I + I G j I < C ^^k j +1 + ^{A j}) ,

d ( F j ,G j ) ^d ( ^x ° ,y }+i )

^j¹/ + Bj) ,     (22)

где C — некоторая положительная константа, оценивающая нормы производных функций F и G из (17).

Оценки (22) показывают, что бесконечная в обе стороны последовательность (18), записанная в перекрестных координатах, является последовательностью сжимающих отображений, каждое из которых определено на компакте. При этом константу сжатия q <  1 можно выбрать одной и той же, именно q ^ k ^{- 1 /n} , где к — минимальный номер полосок o k и о\ в П ^- и П ⁺ .

Таким образом, мы получили следующее утверждение:

Множество неасимптотических в O траекторий из N ^ при 0 С P < P 1 состоит из траекторий седлового типа и находится во взаимно-однозначном соответствии с множеством неасимтотических к (..., 0,... , 0,...) траекторий подсистемы ^ _к топологической схемы Бернулли из двух символов. По построению, это соответствие является гомеоморфизмом.

Отсюда вытекает, что ограничение f µ на множество N µ неблуждающих траекторий из U топологически сопряжено с системой о : Q k ^ ^ к , см. также [17].

Однако заметим, что Nµ содержит также точку O и асимптотические к ней траектории. При p = 0 сама точка O не является гиперболической, как и все ш-предельные к ней траектории из Nµ . Во всяком случае для таких траекторий, так как бесконечное число их точек лежит на Wss : {у = 0, |x| < е}, константа сжатия (для обратных итераций по y ) не отделена от 1. Поэтому в целом множество N0 является здесь неравномерно гиперболическим.

Ситуация сразу резко меняется, если мы рассматриваем случай ^ > 0. Тогда константу сжатия для всех траекторий, проходящих очень близко к O (например, для асимптотических к O траекторий), можно брать равной q ^ nfpe -^k ^ 1 при больших к. Это завершает доказательство основной теоремы.