О существовании центров равнодавлений, являющихся центрами концентрации материальной субстанции

В работах [1-3] Г.С. Гуревичем предложена принципиально новая физическая теория, описывающая устройство и функционирование окружающего нас мира. Эта теория основана на выводе о том, что существуют, так называемые, центры равнодавлений в галактиках, в метагалактиках и во Вселенной, в которых концентрируется материальная субстанция, излучаемая солнцами в галактиках, галактиками в метагалактиках, метагалактиками во Вселенной.

Настоящая статья посвящена математическому исследованию правомерности выводов теории Г.С. Гуревича.

В работе [4] Г.С. Гуревич приводит следующее определение центра равнодавлений: "Центр равнодавления есть точка в пространстве, где равнодействующая сила порожденная давлением материальной субстанции излучаемой другими точками (звездами), равна нулю".

Согласно работе [4] в центре равнодав-лений концентрируется материальная субстанция, поступающая от окружающих излучающих ее точек.

Рассмотрим на частных примерах вопрос о существовании центров равнодавлений и постараемся описать свойства этих центров, исходя из правил векторной алгебры [5].

Случай двух излучающих точек

На рис. 1 приведен пример, описывающий излучение субстанций, идущее от двух точек.

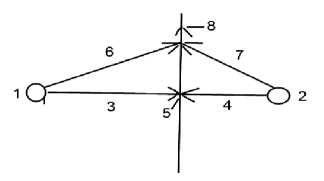
Рис. 1. Схема излучения материальной субстанции двумя точками

Опишем и проведем анализ схемы, изображенной на этом рис. 1.

Пусть излучения происходит из точек 1 и 2. Силы 3 и 4, определяемые давлениями, направлены друг к другу. Пусть точка 5 является центром равнодавлений. Очевидно то, точка 5 находится на прямой, соединяющей точки 1 и 2. Рассмотрим вектора сил 6 и 7, пусть они "сходятся" в одной точке на прямой, перпендикулярной прямой, соединяющей точки 1 и 2. В этом случае направление равнодействующей силы 8, образованной силами 6 и 7, будет направлено в сторону, противоположную центру равнодавлений 5.

Поэтому материальная субстанция не будет концентрироваться в центре равнодавлений 5, созданном излучающими точками 1 и 2.

Излучение материальной субстанции тремя точками

Рассмотрим схему излучения материальной субстанции тремя точками (см. рис. 2).

Пусть угол α является углом между направлением силы 6 и основанием треугольника – отрезка, соединяющего точки 1 и 2.

Пусть общая формула силы, исходящей от точек излучения, задается соотношением

F = k -1- r2

где r – расстояние от точки излучения субстанции до заданной точки пространства.

Легко видеть, что равнодействующая сила Fr сил 5, 6, 7, исходящих из точек 1, 2, 3 и приложенная к любой точке, расположенной на расстоянии x от нижнего основания (см. рис. 2) и находящейся на высоте, исходящей из точки 3 рассматриваемого треуголь- ника, определяется равенством k ksin3α

F r =^h - X ) 2 ^{- 2} x

Исходя из свойств равностороннего треугольника, справедливо соотношение

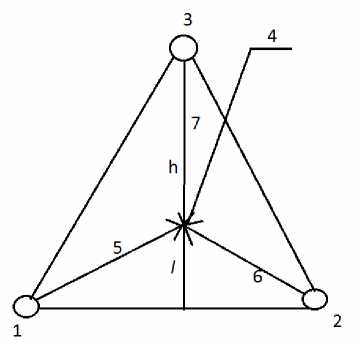
Рис. 2. Схема излучения материальной субстанции тремя точками

a = arctg

X

htg П

V 6 J

_ I 3 x I=arctg I hT3 J.

С учетом равенств (1) и (2) верна формула

k

F r ( h - x ) ²

, • з     _ I 3 x k sin arctg I —;=

L   I h Л x2

. (3)

Очевидно, что для центра равнодавле-ний справедливо равенство

Пусть излучающие материальную субстанцию точки 1, 2, 3 образуют равносторонний треугольник. Очевидно, что центр равно-давлений 4, если он существует, находится на высоте этого треугольника, исходящей из точки 3. Центр равнодавлений 4 обусловлен действиями силы 5 (сила исходит из точки 1), силы 6 (исходит из точки 2) и силы 7 (исходит из точки 3).

Пусть высота рассматриваемого треугольника равна h , а отрезок высоты, соединяющий основание треугольника и центр рав-нодавлений 4, равен l .

Fr = 0 =

k

(h - l )2

- 2

, • 3        . I 3l k sin arctg I —1=

L     I h У3

x ²

. (4)

Заметим, что для центра равнодавлений должно выполняться двойное неравенство

l e ( 0, h ) .                    (5)

Согласно соотношению (4) для вычисления значения l достаточно решить уравнение

arctg

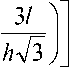
sin3

= 0 . (6)

Вычислительный эксперимент

Пусть h = 10000 .

Для определения корней уравнения (6) воспользуемся электронным on-line ресурсом [6]. Несложные вычисления позволяют из нескольких корней выбрать два, удовлетворяющих условию (5): 1 1 = 1435, 1 2 = 3333. [3].

Таким образом, произведенные вычисления показывают, что в равнобедренном треугольнике, образованном излучающими точками, может быть несколько центров равно-давлений.

Замечание

Отметим, что для концентрации в точке l ₁ материальной субстанции необходимо, чтобы для точки x , удовлетворяющей одновременно условиям x ^ 1 1 , x е ( 0, h ) , были справедливы неравенства F r <  0 для x <  1 1 и F r >  0 для x >  1 1 . Для концентрации материальной субстанции в точке l ₂ необходимо, чтобы для точки x , удовлетворяющей одновременно условиям x ^ 1 2 , x е ( 0, h ) , были справедливы неравенства F_r <  0 для x <  l ₂ и F_r >  0 для x >  l ₂ .

С помощью on-line ресурса [7] был построен график функции (3) при h = 10000 (см. рис. 3).

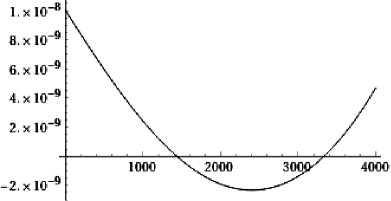
Рис. 3. Равнодействующая сила распространения материальной субстанции

Рисунок 3 демонстрирует, что согласно вышеприведенному замечанию, в центре рав-нодавлений l ₁ не будет происходить концентрация материальной субстанции, но материальная субстанция будет концентрироваться в центре равнодавлений l ₂ .

Так как в равностороннем треугольнике существует три высоты, а центры равнодав-лений, являющиеся центром концентрации материальной субстанции, располагаются на этих высотах на расстоянии от каждого основания, то в этой точке, которая является центром треугольника, существует единственный центр равнодавлений, где происходит концентрация материальной субстанции.

Выводы

Таким образом, в результате вычислительного эксперимента на примере равностороннего треугольника, вершинами которого являются источники излучения материальной субстанции, показано, что точек в пространстве, в которых концентрируется материальная субстанция, может быть несколько и что существует единственный центр равнодавле-ний, где концентрируется материальная субстанция.