О существовании и единственности решения обратной задачи спектрального анализа для самосопряженного дискретного оператора

Пусть дискретный самосопряженный полуограниченный снизу оператор Т с ядерной резольвентой действует в сепарабельном гильбертовом пространстве Н. Предположим, что спектр оператора о(Т), простой и занумеруем собственные числа оператора А_п в порядке возрастания п = 0, ос. Через v_n обозначим соответствующие Х_п ортонормированные в Н собственные функции.

Рассмотрим следующую обратную задачу спектрального анализа: для данной последовательности {Сп}^о мало отличающейся, в некотором смысле, от последовательности {А_п} доказать существование и единственность такого оператора, что его спектр совпадает с данной последовательностью {£_п}-

Будем искать этот оператор в виде суммы Т + Р, где Р — оператор умножения на функцию ре Н действующий в Н. Обозначим: r„ = i min{A_ra+i — A_n; A_n — A_n-i}, To = inf r_n,

'In ⁼ {A ^: l^n ^1 ⁼ ^n}; ^П ⁼ {^ ^: l^n ^1 — ^rn}> ^ ⁼ П ^n-

71=1

Лемма 1. Пусть ||P|| < r/2, где 0 <  r < го, тогда оператор T + P — дискретен и его собственные числа р_п имеют такую же кратность, что и Х_п, причем

(г) если Ro(X) G ©_д, то R(X) G ©_q, 1 <  q < ос,

(И) если A_n G С \ П_г, то р_п G С \ Q_r, где Rq и R резольвенты операторов Т иТ + Р соответственно.

Доказательство. Рассмотрим очевидное операторное тождество, справедливое при всех A G Q:

Т + Р - ХЕ = (Е + PRoWXT - ХЕ).

1                          г

— < -. Значит существует линейный Тп 2

Так как ||.Ro(A)|| = ^у^ур т0 ll^^o(^)II < 2

ограниченный в Н оператор (Р + PPq(A)) ¹ = 52£L_O(^— ^(^^oW)¹¹, причем ряд сходится по норме равномерно по А G Q и ||(Р + Р7?о(А))-¹|| < 2.

Тогда всюду на Q существует линейный ограниченный оператор

RW = (Т + Р- АР)”¹ = Л₀(А)(Р + РЯо(А))-¹.

Отсюда следует, что оператор Р(А) G 69, и для него справедливо разложение в сходящийся по норме ряд

RW = f;(-l)^fcPo(A)(PPo(A))\ А е Q.                    (2)

fc=0

Так как Р(А) — компактный оператор в Н, то оператор Т + Р дискретен. Норма разности проекторов Рисса, при любом n G N

^-J (P(A)-Po(A))dA

<    / 1|Л(А)|| . ||РЯ0(А)|||дА| < -2тггп-^—    < -

2тг ■'Tn                           "^ "п 2г_п т_п

(3) поэтому все корневые подпространства оператора Т + Р имеют такую же размерность, как и у оператора Т.

Кроме того, если A_n G С \ П_п, то д_п € С \ $1_П.

Рассмотрим операторное тождество

Я(А) = Яо(А) - Яо(А)РДо(А) + Р(А)(РР0(А))2, A G Q.

Умножим его на ^, проинтегрируем по контуру 7П и найдем след. В итоге получим следующее утверждение.

Теорема 1. ||Р|| <  ^ то имеет место спектральное тождество

Рп = А_п + (Ри_п, -и^ + а_и(р),

где аДр) = J_7n ASp [Л(А)(РРо(А))²] дА.

Лемма 2. Если ||Pj || < г/2, 0 <  г <  tq, j = 1,2, то

|ап(Р1) - an(p2)| < rrn||Pi - Р2|| max ||Р0(А)||2,

AGTn где || • Ц2 — норма Гильберта-Шмидта.

Доказательство. Введем обозначение ПДХ) = (Т + Pj — ХЕ)^-1, j = 1,2. Умножая ряд (2) на (Р,Яо(А))², получим

ОО

Я(А)(Р,Яо(А))² = 53(-1)^кРо(А)(Р,Р_о(А))^к, A G Q.

к=2

Обозначив через а^ к-ю поправку:

«пЧр) =

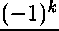
2тгг

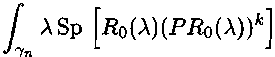
dX =

(~l)fc+1

2itik

Sp[PPo(A)]fcdA,

О существовании и единственности решения...

из (4) получим а_п(р) = ^ а^ (р).

к=2

Оценим разности к-х поправок, к > 2.

l«^fe)01) — «^02)1

= 2^ / Sp [(Р1До(Л)^ ~ №^o(A))fc] dX

Tn — max к AG7n

fc-1

^(P₂7?₀(A))^s№ - РаЛДАДАЯоСА))^⁵-¹

s=0                                                i

( k —1             ^^

ЕИЛ-туД) ~ l№O)ll2№Wll‘”2

5=0                                                     .

r„||Pi -p₂|| Q^k 'max f||Po(A)||i ||Po(A)||^fc-²) . Х2/ AG7„ X                     /

Далее оценим модуль разности:

|«n(pi) -»n(P2)| <  r_n||Pi -P₂||-max||Po(A)||2 V (-) max ЦРоСА)^ <  k=Q

rrn||Pi - Р2|| max ||Ро(А)||2.                                □ хе^п

ОО

Разложим v2 по ортонормированному базису {<Рп}^=о- Тогда и2 = 52 Спк^Рк- Отсюда к=0

получаем (Pv_n,v_n) = 52^=0 ^kPki где Рк — коэффициенты Фурье функции р в базисе {Pn}^o- Перепишем (4): д_п - A_n - o_n(p) = (Pv_n,v_n) и обозначим: а_п = р_п - А_п - а_п(р),

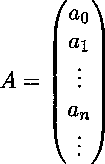
^Ро^

Pi

Рп

С = (су)^₌₀.

Тогда основное спектральное тождество (4) запишется в матричной форме А = СР.

Обозначим элементы обратной матрицы С^-1 через с^-.

Следующая теорема является обобщением результатов работ [1 — 2].

Теорема 2. Если матрица С обратима и для нее выполняется неравенство:

т

\ 9\ 9

оо                        \ z \ 2

52 c2fcrfc ™ах IIд0 (А) II2 )     =ш<1, к^о х^к        / /

то для любой комплексной последовательности {^п} удовлетворяюи^ей неравенству:

ОО /ОО

п=0 \/г=0

2\ 2

<5(1-^,

существует функция р 6 Н, такая, что а(Т + Р) = {^_та}.

Доказательство. В пространстве Н рассмотрим уравнение относительно р;

р = «о — а(р), где

ОО ОО

«О —      ^cnk(^к ^k^nj n=0 А:=0

ОО ОО

«(р) = ^^^спк^ак{р)^рп- п=0 к=0

Введем оператор А : Н -> Н, определяемый равенством: Ар = ао — а^\ Так как Мр11я < ||ао||я + ||«(р)||я < ^(1 — со) + ^ш = 5, то оператор А отображает замкнутый шар U(0. 5) в себя. Покажем, что оператор А сжимающий в этом подпространстве.

Mpi - АргИн = ||«(Р1) - а(р₂)||я =

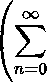
ОО

^Спк^М -«кЫ)

к=0

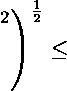
» О\ 9

оо\ \

52l^CnfcH«k(Pl) -»кЫ\ )

/с—О) )

,. 1

/ оо / оо\ I dl^-^ll ^(^|c~Jrfcmax||.Ro(A^ < w||pi-р2||я.

\n=o\t=O Х^к / /

По принципу С. Банаха уравнение (5) имеет единственное решение р.

Определим оператор Р, действующий в Н, следующим образом: Рь(ж) = р(т)ь(ж), гдер - решение уравнения (5). Оператор Р удовлетворяет условиям леммы 1, поэтому оператор Т + Р имеет дискретный спектр а^Т + Р) = {рп}^=о- Кроме того, для этого оператора выполняется основное спектральное тождество (4).