О существовании переходов между стационарными режимами задачи обтекания

Пусть ограниченное тело B С R 3 движется в жидкости, занимающей все пространство вне тела, со скоростью — a(t)e i , где e i — единичный орт оси Ox i . Тогда поле скорости жидкости u = u(x, t) удовлетворяет следующей начально-краевой задаче для системы Навье — Стокса

( д? + (u, V )u = A u — V p,

[divu = 0, uldB(t) = —a(t)ei, u^ = 0, где B(t) — область, занимаемая телом в момент времени t. Здесь, не нарушая общности, считаем, что плотность и коэффициент вязкости равны единице. Полагая

u(x, t) = v

t x + j a(s)e1

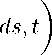
— a(t)e i ,

p(x, t) = r I x

+

t

У a(s)e i

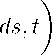
получаем, что v(x,t), r(x,t) удовлетворяют системе

I

^dv + (v, V )v — a'(t)e i = Av — Vr, divv = 0, v | _S Q = 0, v | ^ = a(t)e i ,

в области Q x (0, го ), где Q = R 3 \ B (0).

Пусть v _{α 1} , v _{α 2} — стационарные режимы задачи обтекания, т. е. решения стационарной системы Навье — Стокса в области Q

A v — Vp = (v, V )v, divv = 0, v | q q = 0,

удовлетворяющие соответственно условиям vU = aiei, v|^ = a2ei.

Задачей о переходе между стационарными режимами vα1 и vα2 будем называть задачу об определении решения нестационарной системы Навье — Стокса (2), удовлетворяющего начальному условию v|t=o = va1 и предельному соотношению limt^^ v = va2. В случае ai = 0 получается задача, впервые рассмотренная Р. Финном [1] и названная им «стартовой проблемой». О работах, посвященных этой задаче и имеющихся здесь трудностях смотрите в [2]. В частности, в [2] при ai = 0 и достаточно малом a2 установлено существование в подходящем банаховом пространстве решения стартовой проблемы v(t), удовлетворяющего оценке llV(v(t) — va2 )kL3 6 ct-i/2, kv(t) - va2 IlLq 6 cq t-(i-3/q^/2, q> 3.

2.    Сведение к интегральному уравнению

Будем предполагать, что стационарная система (3) имеет семейство стационарных решений v _a (v _a | ^ = ae i ), гладко зависящих от параметра a при a Е [a i , a 2 ]. (В дальнейшем это условие будет уточнено.) При этом предположении решение задачи (2) будем искать в виде v = v _a(t) + w, r = p _a ( _t ) + q, где a(t) — гладкая функция со значениями на отрезке [a i ,a 2 ], такая, что a(0) = a i , a(t) ^ a 2 при t ^ го . Тогда для определения w имеем следующую начально-краевую задачу в области Q при t >  0

f ^d dw ^{+ (v} a ( t ) , ^{V )w + (w}, ^V)v a(t) ^{+ (w}, ^{V )w - a} 0 ^(t)e i = 4 w ^- V q ^{- a} 0 ^(t) da v a(t) ,

(divw = 0, w|SQ = 0, w|t=o = 0, причем будем требовать выполнения условия w|^ = 0 при всех t > 0.

Введем обозначение va = va — aei. Тогда первое уравнение системы (4) представляется в виде dW + a2diW + (Va2, V)w + (w, V)Va2 + (a(t) — «2) diW + (va(t) — Va2, V)w

-

d                     (5)

^{+ (w}, ^{V )(v} a ( t ) ^— v a 2 ) ^{+ (w}, ^{V )w} = ^{4 w — V}q ^{— a}' ^(t) dav a ( t ) ’

Для дальнейшего исследования удобно свести систему (4) к задаче Коши для ОДУ в подходящем банаховом пространстве. Обозначим через S p = S p (^) (1 6 p 6 го ) подпространство в пространстве векторных полей L _p (Q), являющееся замыканием множества всех гладких соленоидальных полей с компактным в Q носителем. (Заметим, что здесь и далее мы не различаем обозначения для пространств векторных полей и функций.) Известно (см., например, [3, 4]), что для областей класса C ² (в дальнейшем это условие предполагается всегда выполненным) существует ограниченный проектор П : L _p (Q) ^ S p (^) (1 < p <  го ). Применяя его к системе (4) и учитывая (5), сведем ее к следующей задаче Коши для ОДУ в пространстве S _p (Q)

^t. = Aw + B(t)w + Kw + F (t), w|t=o = 0, где операторы A, B(t), K и векторное поле F(t) имеют вид

Aw = П I 4 w — a ₂ d _i w — (v _a 2 , V )w — (w, V )v _a 2

B (t)w = - П^(«(<) - a 2 )d i w + (V a(t) - V a 2 , V )w + (w, V )(v _a ( t ) - V a 2 )J ,       (8)

∂

Kw = - n(w, V )w, F (t) = - П a (t) da^v a(t )j •                  (9)

Рассмотрим действующий в пространстве S p (Q) оператор Озеена

A o = П( 4 - u ^ d i )

с областью определения D(A o ) = S p (Q) П W p2 (Q) П W p (Q).

Здесь Wp(Q), Wp(Q) — соболевские пространства векторных полей, причем элементы из Wp(Q) имеют нулевой след на границе dQ.

Оператор A o порождает в любом пространстве S p (Q) (1 < p <  го ) аналитическую полугруппу T ^ (t), для которой справедливы оценки

/, - Ид' _ 6 Cpq t-|a|/2-3/2(1/p-1/q) , где 1 < p 6 q < го при a = 0; 3/2 6 p 6 q < го при |a| = 1.

При фиксированном значении u ^ = 0 данные оценки установлены в [5] методом гидродинамических потенциалов, в [6] они получены независимо и иными методами, причем доказана их равномерность по параметру u ^ Е (0, r).

Вместе с оператором A o рассмотрим возмущенный оператор Озеена A = A + B , где Bu = - П((u, V )v + (v, V )u).

В [7] для оператора A установлены следующие результаты.

Теорема 1. Если v — соленоидальное поле, причем v,djv Е L^(Q), то возмущенный оператор Озеена A с областью определения D(A) = D(Ao) порождает в любом пространстве Sp(Q), 1 < p < го, аналитическую полугруппу T(t). Если дополнительно v Е Lp(Q), p Е [pi, го], где pi < 3, и при некотором q > 2 возмущенный оператор Озеена A : Sq(Q) ^ Sq(Q) не имеет собственных значений в полуплоскости Re А > 0, то для возмущенной полугруппы Озеена справедлива оценка kT(1)Пд6 ||p_q 6 Cpqt-\6V2-3/2(1/p-1/q>                          (10)

при выполнении следующих условий

|0| 6 1, 1 < p 6 q < го, q > 3/2, причем p > 3/2 при |У| = 1.

Заметим, что из результатов [8] (см. также [9]) следует, что обобщенное решение v _a стационарной задачи обтекания (3) удовлетворяет условиям: v _a Е W p 2 (Q) для всех p Е (2, го ], V v _a Е L _p (Q) для всех p Е (3/2, го ]. Далее, как уже отмечалось, мы предполагаем гладкую зависимость решения v _a при a Е [a i ,a 2 ] (a i ,a 2 > 0) в норме любого пространства L _p (Q) при p Е (2, го ]. Заметим, что локально, т. е. в окрестности фиксированного α данное предположение может быть обосновано методами теории неявных отображений, если для v _α выполнены предположения теоремы 1. При малых числах Рейнольдса (в данном случае при малых α) указанное утверждение можно извлечь из результатов [10]. Сошлемся также на работу [11], где исследован вопрос о гладкой зависимости стационарного решения задачи обтекания от числа Рейнольдса в норме некоторого банахова пространства.

В дальнейшем оператор A вида (7) будем рассматривать как возмущение оператора Озеена с той же областью определения D(A) = D(Ao ) и предполагать выполненными предположения теоремы 1. Аналитическую полугруппу, порожденную этим оператором, будем обозначать T(t). В силу наших предположений для нее справедливы оценки (10) и кроме того даva Е Lp(Q) для любого p £ (2, го].

Формально обращая главную часть ОДУ (6), приходим к интегральному уравнению

w(t) = j | t (t — s) ( B(s)w(s) + Kw(s) )| ds + F(t),               (11)

где

t

F ⁽t) = 1

T(t — s)F(s) ds

а операторы B (t), K и поле F (t) определены в (8), (9).

В дальнейшем решение задачи Коши (6) будем понимать в обобщенном смысле как решение интегрального уравнения (11).

3.    Существование решения задачи о переходе

Предварительно установим ряд оценок для интегральных операторов и поля F(t), входящих в уравнение (11). Всюду в дальнейшем считаем выполненным условие a(t) = a 2 при t > R.

Лемма 1. Справедлива оценка

(1+ t)5kF(t)kq 6 A(p,q,R,5K где

A(p, q, R, 5) = sup

α

∂ vα ∂α

(1 - y)^{- 1} (1 + R) ⁵ R ^1-Y C p,q ^p

c _p,_q — константы из оценки (10), E = max | a ⁰ (t) | , а параметры 5, y , p, q удовлетворяют соотношениям 0 <5 6 y = (3/2)(1/p — 1/q) < 1, 2 < p 6 q < го.

C Используя представления (9), (12) и оценки полугруппы (10), устанавливаем нера- венство

kF ^(t) k q ⁶ c pq ^{E su}P

α

∂ vα ∂α

p

min( t,R )

У (t — s) ^-Y ds.

Остается получить оценку для интеграла

I (t) = (1 + t) ⁵

min( t,R ) /  ^(t

— s) ^Y ds.

В случае t 6 R, осуществляя замену 1 — (1 + s)(1 + t) 1 = u, приводим интеграл I(t) к виду t/(i+t)

I (t) = (1+ t)5+1-Y У u-Y du, из которого ввиду возрастания I(t) на [0, R] получаем

R/ (1+ R )

I (t) 6 (1 + r) ^{5+1 - y}   у .

«7 ... = R 'R

^{1 —} Y

.

В случае t > R интеграл I (t) убывает при возрастании t. Поэтому

R

I (t) 6 (1 + R) ⁵ J (R - s) ^-Y ds =

R ^1-Y (1 + R) ⁵

^{1 —} Y

.

Утверждение леммы следует из установленных оценок (13)–(15). B

Для оценок интегральных операторов введем банахово пространство Xδ,q векторных полей из C([0, го), Sq(Q)) с конечной нормой llu|5,q = SUp(1 + t)5 ku(t)kq.

t

Лемма 2. При 0 <5 6 1/2, q >  3/2 для оператора

t

Bu(t) = У T (t — s)B(s)u(s) ds

справедлива оценка

WUkq 6 24C q,q dR ^1/2 k u k ₅,q , где c q,q — константа из оценки (10),

d = max d(t), d(t) = | a(t) — a 2 | + 2 k V a ( t ) — V a 2 k ^ -

C Используя оценки (10) с | 0 | = 1, получаем неравенство

t kBu(t)kq 6 3Cq,q У(t — s)-1/2d(s)(1+ S^-ds^uk^.q,   q> 3/2.

Учитывая, что функция d(t) отлична от нуля лишь на отрезке [0, R], приходим к выводу, что достаточно оценить интеграл

min( t,R )

J (t) = (1 + t)⁵ j (t — s) ^1/2 (1 + s) 0

^δ ds.

Применяя рассуждения, аналогичные доказательству леммы 1, получаем оценку (1 + t) ⁵ J (t) 6 8R ^1/2 .

С учетом (16) приходим к утверждению леммы. B Лемма 3. Для оператора

t

K u(t) = j T(t — s)Ku(s) ds, 0

где K определен в (9), при выполнении условий p > 3, q > 3/2, 0 6 2/p - 1/q < 1/3, 0 < в < 1/2, 0 6 5 6 2в + (3/2)(2/p - 1/q) - 1/2

справедлива оценка kKukq 6 C(e,5,p,q)kuke,p, где

C(e,5,p,q) = 3cp/2,qB(1 - a, 1 - 2в), cp/2q — константа из оценки (10), a = (3/2)(2/p - 1/q) + 1/2, B(•, •) — бета-функция Эйлера, определяемая формулой

B(а,в) = j (t - s) ^a-1 s ^e-1

ds.

С Вследствие оценок полугруппы T (t) справедливо неравенство

t kK u(t)kq 6 3cp/2,q кикв„ J (t - s)-a(1 + s)"^ ds.                 (17)

Теперь, осуществляя в интеграле

t

I(t) = j(t - s)-a(1 + s)-2e ds замену переменной 1 - (1 + s)/(1 + t) = a, получаем t/(1+t)

I (t) = (1 + t) ^1-a-2e j a ^-a (1 - a) ^-2e da 6 (1 + t) ^1-a- 2 ^e B (1 - a, 1 - 2в).     (18)

Комбинируя (17) и (18), приходим к заключению леммы. B

Следствие 1. При выполнении условий q > 3 и 1/2 - 3/(2q) 6 5 < 1/2 справедливы неравенства kKukq 6 C(5, 5,9,q)kuk2,q,

||K U 1 - KU 2 k »,q 6 2C(5, 5, q, q) max ku j Ц ^,, k u i - ^k^q .

j

Для исследования вопроса о разрешимости уравнения (11) воспользуемся следующей леммой.

Лемма 4. Пусть X — банахово пространство, B : X ^ X — линейный ограниченный оператор и kBk 6 1/2, Q : X ^ X — нелинейный оператор с оценками kQuk 6 b||u||2,   kQui - Qu2k 6 bmax kukkui - «2k- j

Тогда уравнение u = Bu + Qu + g при выполнении условия kgk 6 1/(16b) имеет единственное решение в шаре {u : |u| 6 1/(4b)}.

C При указанных предположениях шар { u : ||u k 6 1/(4b) } инвариантен относительно отображения u i^ B u + Q u + g, являющегося сжимающим в этом шаре. Поэтому утверждение леммы следует из теоремы Банаха о неподвижной точке. B

Вернемся к уравнению (11). Справедлива следующая

Теорема 2. Пусть существует гладкое семейство стационарных решений v _α , α ∈ [a i ,« 2 ] задачи обтекания, причем v _a 2 таково, что при некотором q >  2 возмущенный оператор Озеена A : S q (Q) ^ S q (Q) вида (7) не имеет собственных значений в полуплоскости Re А > 0. Тогда для любых фиксированных чисел q, p, 6, удовлетворяющих условиям q >  3, p >  2, 1/2 — (3/2q) 6 6 < min(1/2, (3/2)(1/p — 1/q)), существует такое П = n(q,P, 6), что при | a i — a ₂ | 6 n уравнение (11) имеет единственное решение w Е X s,q •

C Заметим, что уравнение (11) можно представить в виде w = Bw + Kw + F (t), где операторы B, K и поле F определены соответственно в леммах 2 и 3 и в (12). Будем считать, что a(t) = ai + («2 — ai)t при t Е [0, R] и a(t) = «2 при t > R. Тогда при заданных q, p, δ в силу лемм 1, 2 и следствия из леммы 3 выполняются неравенства kF kδ,q 6 A|α1 - α2|, kBukδ,q 6 B|α1 - α2|kukδ,q, kKuks,q 6 Ckuk2q, |Kui — Ku2lkq 6 2Cmax ku ks,q|ui — u^q. j

Вследствие установленных оценок существование решения вытекает из леммы 4.

0 6t6T

Тогда аналогично предыдущим рассуждениям устанавливаем неравенство llwkq,T 6 c(T)kwk^,q,T, в котором c(T) ^ 0 при T ^ 0. Поэтому w(t) = 0 в окрестности точки t = 0.

Пусть £ = max T всех таких T , что w(t) = 0 при t 6 T.

Очевидно, что £ = го , иначе аналогично предыдущему

NW 6 d(T — e)kwk^,q,T при T > (, где d(T — () ^ 0 при T ^ £. Но тогда w(t) = 0 на более широком отрезке чем [0, ^], что противоречит определению ^. Этим завершается доказательство теоремы. B

Замечание. Можно считать a(t) произвольной гладкой функцией и дополнительно требовать малости sup | a ⁰ (t) | при t Е [0, R].

4.    Оценки сходимости к стационарному режиму

Дальнейшей целью является получение оценок норм разности v(t) — va2, где v(t) — решение системы (2), при t ^ го. Учитывая, что при t > R v(t) = va2 + w(t), приходим к необходимости оценки норм w(t). Для этого будет исследован вопрос о принадлежности решения w уравнения (11) пространствам Xµ,r. В этом случае мы не предполагаем малости решения и, следовательно, малости разности |ai — «2/ а используем лишь его принадлежность одному из пространств Xg,q, в котором существует согласно теореме 2 малое решение.

Ниже существенно используется следующая лемма.

Лемма 5. Оператор I — B, где B определен в лемме 2, обратим в любом пространстве X g,_q при всех q > 3/2 и всех 6 6 1/2.

C Ввиду соотношения

(Bw)(t) =

/

min( t,R )

T(t — s)B(s)w(s) ds

достаточно доказать однозначную разрешимость уравнения

t

w

^{( t ) —}/

T(t — s)B(s)w(s) ds = f (t)

в пространстве C([0, T],S_q (Q)). Этот факт является следствием того, что оператор B имеет нулевой спектральный радиус в пространстве C ([0,T ],S_q (Q)) при q >  3/2. B

Пусть w — решение уравнения (11) из пространства X g,_q , где q — одно из чисел интервала (3, го ), а 6 — одно из чисел, удовлетворяющих неравенству 1/2 — 3/(2q) <  6 <  min(1/2, (3/2)(1/2 — 1/q)). Существование малых решений с такими 6, q доказано в теореме 2. Предварительно покажем, что w G X ^,_q при заданном q и всех ц < min(1/2, (3/2)(1/2 — 1/q)). Для элемента Kw имеем в силу леммы 3 включение K w G X _pq , где ц — любое число, удовлетворяющее неравенству ц < 6 i = 26 + 3/(2q) — 1/2. Применяя лемму 5, получаем, что для w справедливо включение w G X _pq при ц < min(6 i , 1/2). Если 6 i > 1/2, то указанное свойство доказано. В противном случае, повторяя приведенное рассуждение, устанавливаем, что Kw и, следовательно, w принадлежат X _pq при всех ц <  min(1/2, 6 2 = 26 i + 3/(2q) — 1/2). Так как последовательность 6 n = 26 _n- i + 3/(2q) — 1/2 обладает свойством 6 n — 6 _n- i = 6 _n- i + 3/(2q) — 1/2 >  6 + 3/(2q) — 1/2 > 0, то при некотором n 6 n становится больше 1/2, что опять влечет выполнение нужного свойства.

Приведенный метод рассуждений обычно называют шнуровкой. Таким образом, шнуровка приводит к следующим выводам: так как при 3 < q 6 6 имеем (3/2)(1/2 — 1/q) 6 1/2, то w G X ^,_q при всех ц < (3/2)(1/2 — 1/q); в случае q > 6 w G X ^,_q при всех ц < 1/2.

Следующие рассуждения показывают, что из принадлежности решения w одному из пространств X g,_q следует его принадлежность некоторой совокупности пространств X ^,r . Ввиду предыдущего заключения можно считать, что 6 < min(1/2, (3/2)(1/2 — 1/q)) и сколь угодно близко к этому числу.

Рассмотрим отдельно два случая 3 < q 6 6 и 6 < q <  го .

В первом случае (3/2)(1/2 — 1/q) 6 1/2, а F(t) в силу леммы 1 принадлежит всем пространствам X ^,r для всех r > 2 и ц < (3/2)(1/2 — 1/r). Ввиду леммы 3 Kw принадлежит всем пространствам X ^,r для всех ц и r, удовлетворяющих условиям 0 6 2/q — 1/r < 1/3, ц < 26 + (3/2)(2/q — 1/r) — 1/2. Учитывая выбор 6, получаем, что можно считать, что ц сколь угодно близко к числу 2((3/2)(1/2 — 1/q)) + (3/2)(2/q — 1/r) — 1/2 = (3/2)(2/3 — 1/r). Следовательно, согласно лемме 5 w(t) G X ^,_r для всех ц и r, удовлетворяющих неравенствам ц < (3/2)(1/2 — 1/r), 0 6 2/q — 1/r < 1/3. Применение шнуровки приводит к заключению, что в первом случае w(t) G X ^,_r при всех r, ц, удовлетворяющих неравенствам 3 < r 6 6, ц < (3/2)(1/2 — 1/r).

Далее, выбирая q достаточно близким к 3 и повторяя предыдущее рассуждение, устанавливаем, что w G X ^,r для всех r £ (2, 3], ц < (3/2)(1/2 — 1/r).

Таким образом, установлено, что в первом случае w £ X ^,r для всех r £ (2, 6], ц < (3/2)(1/2 — 1/r).

Заметим, что этот результат нельзя улучшить.

Обратимся ко второму случаю q £ (6, го ). Так как w £ X _pq для всех ц < 1/2, то в силу лемм 3 и 5 w £ X ^,_r для всех r >  6, r £ [q/2, го ), ц < 1/2. Следовательно, применение шнуровки, если это необходимо, приводит к включению w £ X ^,_r для всех r £ (6, го ), ц < 1/2.

Далее, если w £ X §,_q , где q достаточно близко к 6, а 6 >  1/2 — 3/(2q), то w £ X ^, _r для всех ц, r с условиями 0 6 2/q — 1r < 1/3, ц < min(1/2, (3/2)(1/2 — 1/r)). Здесь важно, что r может принимать значения как большие, так и меньшие 6.

Учитывая изложенное, приходим к выводу: из принадлежности w одному из пространств X§,q, где параметры удовлетворяют условиям q £ (3, го), 6 £ (1/2 — 3/(2q), min(1/2, (3/2)(1/2 — 1/q))), следует, что w £ X^,r при всех r > 2, ц < min(1/2, (3/2)(1/2 — 1/r)).

В отличие от первого случая при q £ (6, го ) граница для ц может быть улучшена. Учитывая последнее утверждение, для Bw имеем оценку

k(Bw)(t)k r 6 С , (1 + t) ^-^                               (19)

для всех r > 2, ц <  1/2 + (3/2)(1/2 — 1/q).

В то же время согласно лемме 3 справедлива оценка

k (Kw)(t) k r 6 c r,^ (1+ t) ^-^                              (20)

для всех r >  6, ц < 1/2 + (3/2)(1/3 — 1/r) = (3/2)(2/3 — 1/r). Ввиду того, что показатели для ц в (19), (20) больше, чем показатель для F(t) (см. лемму 1) окончательно получаем, что при всех r > 6 w £ X ^,_r при всех ц < (3/2)(1/2 — 1/r).

Таким образом, установлена

Теорема 3. Пусть w — решение уравнения (11), принадлежащее одному из пространств Xg,q при выполнении условий q > 3, 1/2 — 3/(2q) < 6 < min (1/2, (3/2)(1/2 — 1/q)).

Тогда w £ X ^,_r для всех r > 2, ц < (3/2)(1/2 — 1/r) и, следовательно,

||v(t) — V a 2 k r 6 C r,^ (1 + t) ^-^

при r > 2 , ц < (3/2)(1/2 — 1/r).