О связи достаточных условий регуляризуемости интегральных уравнений

.    1963 .

[1] . .                                                                                                                                                         .-

,                                                                                                                                                                                .-

,                                                                                ,                                                               .[2]

.,

.

[3–11]                                                              ,-

.

[12–14] .

Достаточные условия регуляризуемости линейных обратных задач

Пусть E и F - банаховы пространства, A : E ^ F - линейный непрерывный инъективный

.

Определение 1. Отображение A 1 называется регуляризуемым, если существует семейство отображений R° : F ^ E, 5е(0,50) такое, что для любого x е E lim sup R у - x = 0 .

5 >0| y - Ax |< °" °       "

В этом случае семейство { R° } называется регуляризатором для A ¹. Операторное уравнение Ax = у называется регуляризуемым, если регуляризуемо отображение A ¹. В случае регуляризуемости уравнения семейство x° = R°y° может быть взято в качестве удовлетворительного приближенного решения некорректной задачи нахождения решения уравнения первого рода при приближенно заданной правой части у° с точностью 5.

Рассмотрим классическую ситуацию E = C (0,1), F = L 2 (0,1). Будем предполагать, что опе-

A                             L2 -       .                    A                                        - рывности на различные подпространства M , C (0,1) с M с L2 (0,1).

В работе [2] было показано, что если продолжение A на некоторое Lp (0,1), p > 2 имеет конечномерное ядро, то отображение A ¹ регуляризуемо.

Теорема 1. Если интеграленый оператор A : C (0,1) ^ L ₂ (0,1) инъективен и его ерооогже-ние на некоторое L_p (0,1) , p > 2 имеет конечномерное ядро, то A ¹ регуляризуемо.

,                                                                                                                                                          .                                   - ная серия условий при разных p > 2. Возникает вопрос, не будут ли какие-то из этих условий

Менихес Л.Д.                                                 О связи достаточных условий регуляризуемости интегральных уравнений эквивалентными, если рассматривать не произвольные операторы A, а интегральные операторы с гладкими симметричными ядрами.

В работе [14] был дан отрицательный ответ на этот вопрос. Оказалось, что все рассмотренные в теореме 1 достаточные условия попарно не эквивалентны.

В работе [13] доказывается такое усиление теоремы 1.

Теорема 2. Если интегральный оператор A : C (0,1)^ L ₂ (0,1) инъективен и его еродолже-ниена L „„( 0,1) имеет конечномерное ядро, то A ¹ регуляризуемо.

Здесь также возникает естественный вопрос, не будут ли какие-нибудь достаточные условия из теоремы 1 эквивалентны достаточному условию из теоремы 2, если ограничиться операторами с гладкими ядрами. Из теоремы 3 следующего пункта следует отрицательный ответ на этот вопрос .

Сравнение условий регуляризуемости

Пусть K ( x , t ) - непрерывная функция на квадрате [0,1]х[0,1]. Рассмотрим интегральный оператор

Q : f ( x )^ J K ( x , t ) f ( t ) dt ,                                  (1)

действующий из C (0,1) в L2 (0,1). Через Q обозначим продолжение Q на L2 (0,1). Оператор Q предполагается инъективным, так как здесь будет идти речь о регуляризуемости Q 1. Опера- тор Q может и не быть инъективным.

Теорема 3. Существует инъективный интегральный оператор из C (0,1) в L ₂ (0,1) с гладким симметричным ядром, продолжение которого по непрерывности на любое Lp (0,1) , p > 2 имеет бесконечномерное ядро, а продолжение на L ° (0,1) имеет конечномерное ядро.

Заметим, что здесь слово ядро используется в двух различных смыслах, но из контекста ясно, что имеется в виду.

Доказательство. Рассмотрим последовательность промежутков

k

1 — Л,1 —1г , k = 1,2,....

2 ^k ’     2 ^{k +1}J’        ’

Определим следующую последовательность функций. Через hk ( x ) обозначим функцию на [0,1] сносителемв J_k и такую, что hk ( x )е Lk ₊₁ (0,1), но hk ( x )ё Lk ₊₂ (0,1), k = 1,2,....

Через M обозначим наименьшее замкнутое подпространство L2 (0,1), содержащее все функции hk (x). Пусть C° ( a, b) - подпространство C (a, b), состоящее из финитных функций, т.е. бесконечно дифференцируемых и равных нулю в окрестностях точек а и b. Для доказательства теоремы рассмотрим следующую лемму из [2].

Лемма 1.Пусть h(t)е L2 (а,b) и b

H =

] f ( t )^е L 2 ( а , b ): J f ( t ) h ( t ) dt = 0^.

[                        a                      J

Тогда

H П C 0~( a , b ) = H .

Теперь покажем, что в ортогональном дополнении N к M существует полная ортонорми-рованная система {yn ( t )} ^такая, ^41-0 Cn ( t )^е Cо( 0,1), n = 1,2,.... Для этого убедимся, что

Математика

независимую последовательность, ортогонализируя которую мы и получаем нужную систему {Vn ( t )} ■

Пусть f е N и е > 0 ■ Выберем номер n так, чтобы

• ¹                      с²

Г     f ² ( t ) dt < — ■                                   (2)

• 2    n + 1 1J 2 n + 1

Поскольку f ( t ) ортогональна hk ( t ), k = 1,2,..., в силу леммы 1 существует семейство { f_k ( t ), k = 1,2,..., n }, для которого выполняются следующие условия:

• 1.    fk ( t )е C °( Jk ), к = 1,2,..., n ;

• 2.    J fk ( t ) hk ( t ) dt = 0, k = 1,2,..., n ;

  
  

• 3.    f - f l < — ^— -, k = 1,2. ^k J ^J-    2 ( n +1)

  n ,

  
  

Jk

где через fJ обозначено сужение f ( t ) на промежуток J_k . На промежутке J ₀ = 0,1 сущест- ^k                                                                                   2

вует функция f , е C 0 ° (0,12) такая, что

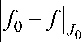
< -— 2 ( n +1)

Теперь рассмотрим функцию

fk ( t )^ПР^{H t е} Jk , ^k = ^0,1,.

n ;

g ⁽ t ) = ‘

при t е

2 n ⁺¹ -1

2 n ⁺¹ ,

В силу (2) и (3) g е C0° (0,1), g е N , так как для любого k = 1,2,...

J g ( t ) hk ( t ) ^dt = J g ( t ) hk ( t ) ^dt = ⁰,

0                    Jk

а значит и для любого m е M

J g ( t ) m ( t ) dt = 0.

Наконец, из соотношения

II g — f l

J ( g - f )² dt <  0

, it J⁽ g ^{- f )2 dt +} ^ T <

\^k =⁰ Jk                 ⁴

< it I J ( g - f )² dt ^k=⁰\ Jk

е . .Д    е е

+— <       +— = е

2 k “ 0 2 ( n +1) 2

следует, что N П C° (0,1) = N .

Теперь рассмотрим интегральный оператор Q (1) с ядром

ОО

K ( x , t ) = t anVn ( x>n ( t ) ,                                ⁽⁴⁾

n = 1

где { ^n ( x )} - произвольная ортонормированная система из бесконечно дифференцируемых на [0,1] функций, {y_n ( t )} - построенная выше система и

Менихес Л.Д.

О связи достаточных условий регуляризуемости интегральных уравнений an = I sup max к 0< x <1

х-1

( ^pn ( ^x )|,-, \)(^x))J

sup max (| ^n ( t )|

0 < t < 1       '

y• n

⁽ t ))

- 1

n

- 2

,              (4)                                                                               ,                              - членным дифференцированием произвольное число раз, и, следовательно, K (x, t) - бесконечно дифференцируемая функция на квадрате [0,1] х [0,1].

Теперь покажем, что ker Q = M . Действительно, если

• ¹    те

JZ anPn ( ^XУн ( t ) f ( t ) ^dt = ⁰,                               ⁽⁵⁾

0 n = 1

TO

Z anbnPn ( ^X ) = ⁰,                                      ⁽⁶⁾

n = 1

где bn = J f ( t )^_n ( t ) dt - n -й коэффициент Фурье функции f ( t ) по системе {yn ( t )}, так как ряд 0

в формуле (5) по теореме Лебега можно почленно интегрировать. Из (6) следует bn = 0, n = 1,2,..., т.е. f ( t )е M . Ясно также, что из f ( t )е M следует f ( t )е ker Q . Таким образом доказано , что ker Q = M . Для того, чтобы ядро Q было симметричным, достаточно положить p_n = y_n . Отсюда следует, что Q удовлетворяет условиям теоремы. В самом деле, продолжение Q по непрерывности на любое L_p (0,1) имеет бесконечномерное ядро, так как оно содержит все функции hk , начиная с некоторого номера. А продолжение Q на L _те (0,1) имеет нулевое яд

,                M                      ,                                              ,                         ..

,

• 1                                                       2                          ,-

• ме 3 оператора Q теорема 1 не дает ответа о регуляризуемости Q 1, в то время как из теоремы 2 следует регуляризуемость Q 1.