О связи имитационной логит-динамики в популяционной теории игр и метода зеркального спуска в онлайн оптимизации на примере задачи выбора кратчайшего маршрута

• 1.    Введение

• 2.    Метод зеркального спуска для задач стохастической онлайн оптимизации с неточным оракулом

В литературе по онлайн оптимизации почетное место занимает так называемая «Задача о выборе кратчайшего пути» («The Shortest Path Problem»), см., например, п. 5.4 [1]. Основной результат здесь заключается в описании «оптимальной» стратегии пользователя транспортной сети (на базе алгоритма «Follow the Perturbed Leader»), из дня в день выбирающего маршрут следования, исходя из истории загрузок графа транспортной сети.

В литературе по равновесной теории транспортных потоков наиболее популярными являются модели равновесного распределения потоков по путям. Одной из первых (и по-прежнему наиболее популярных) моделей такого рода является модель Бекмана [2] (также называемая BMW-моделью). Современные исследования этой модели связаны с ее пониманием как популяционной игры загрузок (как следствие, потенциальной игры [3]), поиск равновесия (Нэша) в которой сводится к задаче выпуклой оптимизации. Упомянутый эволюционный подход, в частности, приводит к изучению различных естественных динамик (наилучших ответов, репликаторов, имитационной логит-динамики и др.), отражающих «нащупывание» пользователями транспортной сети равновесия [4]. Все эти динамики положительно коррелированы с антиградиентной динамикой, поэтому все они приводят в конечном итоге к одному и тому же равновесию (или в более общем случае к одному и тому же множеству равновесий). Тем не менее возникает желание глубже разобраться с природой этих динамик, понять, чем та или иная динамика дополнительно (помимо отражения рациональности игроков/пользователей транспортной сети) примечательна.

В данной работе мы постараемся изложить, чем примечательна имитационная логит-динамика, пояснив ее связь с алгоритмом поведения «Follow the Perturbed Leader», а точнее, с переформулировкой этого алгоритма на языке современной выпуклой онлайн оптимизации: с методом зеркального спуска [5–11].

В разделе 2 статьи описаны различные варианты классического метода зеркального спуска применительно к задачам стохастической онлайн оптимизации с шумами. Ввиду последующих приложений мы сосредоточимся на множествах вида симплекса и прямого произведения симплексов. Хотя во многом эти результаты ранее были известны, тем не менее в такой общности, в которой они приведены в данной статье, нам не удалось найти точной ссылки, поэтому было решено посвятить этому отдельный раздел 2. В разделе 3 мы используем результаты раздела 2 (в данной статье не в максимальной общности) для объяснения имитационной логит-динамики, возникающей при описании поведения пользователей транспортной сети в модели Бекмана.

Сформулируем основную задачу стохастической онлайн оптимизации с неточным оракулом. Требуется подобрать последовательность {ж^} G Q так, чтобы минимизировать псевдорегрет [6–11]:

• 1    ^N                 1 ^N

Regret tv (^{ffe ⁽ • ^{) }} , {^ж/г}) = — ^ ^f k (V) - m a in — ^ f k ^{(ж)             (1)}

• ^V k=1            x 4 N _{k =1}

на основе доступной информации:

{Vx/1 (ж1^1) ;...; VxA-1 (ж^Леfc-1)} при расчете жк. Причем выполнено условие :1

• 1)    для любых к = 1,..., — (S ^{fc -1} - сигма алгебра, порожденная е ¹ , • • •, е^ ^-1 )

\\v _xfk ( х ^к ,£^к) -V / к х Л^к) ||* 6 5, E ■ \к (х ^к ,Е )] = V / к (х ^к ) .

Здесь случайные величины {^^к} могут считаться независимыми и одинаково распределенными. Онлайновость постановки задачи допускает, что на каждом шаге к функция /к ( • ) может выбираться из рассматриваемого класса функций враждебно по отношению к используемому нами методу генерации последовательности {х^к}. В частности, /к ( • ) может зависеть от

{_ж 1 ,е 1 ,/ 1 ( • );...; _Ж ^к - 1 ,^ ^{к -1} ,/к - 1 ( • );х ^к} .

Относительно класса функций, из которого выбираются { / к ( • ) } , в данной работе будем предполагать выполненными следующие условия :

• 2)    { / к ( • ) }  - выпуклые функции;

• 3)    для любых к = 1,..., N , х Е Q

v ■ . (х,е)\ \ 2 6М 2 .

Опишем метод зеркального спуска для решения задачи (1) (здесь можно следовать огромному числу литературных источников, мы в основном будем следовать работам [12, 13]). Введем норму |||| в прямом пространстве (сопряженную норму будем обозначать ||П*) и прокс-функцию d (х), сильно выпуклую относительно этой нормы, с константой сильной выпуклости не меньше 1. Выберем точку старта х1 = arg mind (х), XEQ считаем, что d (х1) = Vd (х1) = 0.

Введем брэгмановское «расстояние»

V x (у) = d (у) - d (х) - (V d (х), у - х} .

Везде в дальнейшем будем считать, что d (х) = Vxi (х) 6 В для всех х Е Q.

Определим оператор «проектирования» согласно этому расстоянию:

Mirrx k ⁽9) = ^arg m l in { ( 9, У ^-хк) + ^V x ^k (у) } .

Метод зеркального спуска (МЗС) для задачи (1) будет иметь вид, см., например, [13]:

х ^{k +1} =Mirr _x k (a V _x / _к (х ^к , ^ ^к )) , к = 1,..., N.

Тогда при выполнении условии (2) для любого и Е Q, к = 0,..., N — 1 имеет место неравенство, см., например, [13]:

а ( V x/к (х ^к , Е ) , хк - и ) 6 ^ || V x / к ^ , Е ) 112 + V x _k (и) - V x _{k +}1 (и).

2/2

Это неравенство несложно получить в случае евклидовой прокс-структуры d (х) = | х |

• [14]    (в этом случае МЗС для задачи (1) есть просто вариант обычного метода проекции

градиента). Разделим сначала выписанное неравенство на а и возьмем условное математическое ожидание E^k+i [ • | Нк], затем просуммируем то, что получится по к = 1,...,N, используя условие 1. Затем возьмем от того, что получилось при суммировании, полное математическое ожидание, учитывая условие 3. В итоге, выбирая и = ж* (решение задачи

N

52 f k (ж) ^ min), получим при условиях 1, 2, 4 [11]:

к =1     №

N • Е [RegretN ( { fk ( • ) } , {ж ^к })] 6 ^^ - ^М ₊ Q м 2 _{а +} R ₈^n 6

6?+( 2м 2 “+R6)N- выбирая2

R р2 а = М\N, получим

^Е [RegretN ( ^{{ f}k⁽ • ^{) }} , {^{ж к} })] ^{6 MR}J Nn + ^R 5.

Немного более аккуратные рассуждения (использующие неравенство Азума–Хефдинга) позволяют уточнить оценку (2) следующим образом (см., например, [15]):

RegretN ( { fk ( • ) } , {ж ^к }) 6 Ма^² (R + ^2jR VM ^ ¹ )) -I           (3)

с вероятностью не меньше 1 — ст.

Оценки (2), (3) являются неулучшаемыми с точностью до мультипликативного числового множителя. Причем верно это и для детерминированных (не стохастических) постановок, в которых нет шумов (5 = 0), при этом можно ограничиться классом линейных функций [1].

Рассмотрим три примера, которые понадобятся нам в дальнейшем [11, 15].

Пример 1 (симплекс). Предположим, что

Q = S n (1) =

{ж >  0:

п         Л

Еж. = 1 .

. =1        )

Выберем

п

IHI = IH^, d (ж) = 1n n + У^ж. 1п ж..

. =1

Тогда МЗС примет следующий вид (а = М ¹ ^21n n /N):

ж1 = 1/n,   г = 1,..., n, при к = 1,..., N, г = 1,..., n

( А дЛ(жг ,§г )\         к (    8Jk(xk^k )\ exp |^— ^ а)      жк exp -а  vd$1   )

'Е е( 5^ о⁸^^{( х Т} ,^ ^Г) ^ 5^ ж ^к exп (— а ^Э ^ к ^{( ж к} ,^ ^к ) А Zx^ ^exp I ^— 2_^^а —s^i— ) ^^ж/ ^{exp а} Эх і J

Оценки псевдорегрета будут иметь вид

^Е [RegretN ( ^{{ f}k ⁽ • ^{) }} , {^{ж к} })] ^{6 М}^ ^N^ ^{+ 2 5,}

RegretTV ( { /к ( • ) } , {x ^k }) 6 ^M\PN ( ^ inn + Win (ст 1 )) + 25 с вероятностью не меньше 1 — с.

Пример 2 (прямое произведение симплексов). Предположим, что x = (z1,

..

.,<) e Q

m

= П ^S n ₃ (d j ).

j=1

Выберем

m

0 x 0 = . £ V 0 1 , N 3=1

d (x)=£ m⁽a j =1

n NA ^d3 (z ^{3 )} = ^d j in n + £ ^ln (dj) ■

Тогда, вводя обозначения

R p2 ^a = mN N,

R ²

m

£ d2 in nj, j=1

МЗС можно записать следующим образом:

4 = ^d j ^{/ n} j ,

г = 1, ...,n j ,

при к = 1,..., N, г = 1, ...,n j , j = 1,..., m

3,к +1 A

= ^d j

( к ^exp ^— X ^a \ r=1

^3 ,^ ) ^dz i

)

x ^ exp

n      к   к

X exP — X a

1=1      \ r=1

->Г'хл

^8z i

— = dj —

\

)

/1=1

-- a ^

k (    9Jk (xk,^ )\ ■ x exp (-a N )

Оценки псевдорегрета будут иметь вид

Е

R ^R egretv (^{/к ⁽ • ^{) }} ,

m

{^{x; k} })] 6H _N А £ ^d j ^{ln n} j ⁺²⁵ \ j=1

N

m

£ d2, j=1

Regretv ^{{ /}fk ⁽ • ^{) }} ,

m

{^{x k} }) ^6Mv n (\^{£ d} 2 ^ln

\ N з =1

m nj+4^ £ d2 vin(c-1)

+ 25^

m

£ dj j=1

с вероятностью не меньше 1 — т.

Пример 3 (выбор среди вершин симплекса). Вернемся к примеру 1 и будем дополнительно считать, что по условию задачи {x^k} должны выбираться среди вершин единичного симплекса S _n (1). Так же, как и раньше, онлайновость постановки задачи допускает, что на каждом шаге к функция / к может подбираться из рассматриваемого класса функций враждебно по отношению к используемому нами методу генерации последовательности {x^¹}. В частности, / к может зависеть от

{x1,^1,/1(•); ...;xk-1,^k-1,/k-1(•)} и даже от распределения вероятностей рк, согласно которому осуществляется выбор x/c. Чтобы можно было работать с таким классом задач, нам придется наложить дополнительные условия :

• 4)    /к (x) = (J^k ,x), к = 1,...,N.

• 5)    На каждом шаге генерирование случайной величины ж ^к согласно распределению вероятностей р ^к осуществляется независимо ни от чего. Выбор /к осуществляется без знания реализации ж ^к .

Следуя примеру 1, положим р ¹ = ж ¹ = ^, г = 1, ...,п. При к = 1, ...,N , г = 1, ...,п согласно распределению вероятностей (а = М ^-1 ^ 2lnn/N)

( А эДх' ,0 Л      к (  эЦхк Д А exp — £ а 1             Pi exP —а   дхг рк+1 = ____£^=________/  = ______V/

*     £ ex"P (— Д “■)   gP-'exP (-«')’ генерируем случайную величину г (к + 1) и полагаем ж^+і) = 1, жк+1 = 0, j = г (к + 1).

Оценки псевдорегрета будут иметь вид

Е [Regret^ ( { /к ( • ) } , {ж ^к })] 6 М ^2 n " + 25,

Regret V ({/к ( • ) } , {ж ^к }) 6 M^N ( V lnn + б^іп (ст ^-1 )) + 25

• с вероятностью не меньше 1 — ст.

• 3.    Приложение к задаче о выборе кратчайшего пути

Рассмотрим транспортную сеть, которую будем представлять ориентированным графом ( V,E ) , где V - множество вершин, а Е - множество ребер. Обозначим множество пар источник-сток через OD С V 0 V ( | OD | = m); d _w - корреспонденция, отвечающая паре w; ж _р - поток по пути р; P _w - множество путей, отвечающих корреспонденции w, Р = U P _w w e OD - множество всех путей. Обозначим через L - максимальное число ребер в пути из Р . Будем считать, что затраты на прохождениe ребра е Е Е описываются неубывающей (и ограниченной в рассматриваемом диапазоне значений) функцией

0 6 Те (/е) 6 м, где /е - поток по ребру е:

/е ^(ж) = ^ ⁵ ер ^ж р , ⁵ ер = I о _е Е р

P E P                 ^V

Положим М = ML. Введем G _P (ж) - затраты на проезд по пути р:

^GP (ж) = ^2^те (/е (ж)) 5 ер .

e E E

Введем также множество (прямое произведение симплексов), на котором транспортная сеть «будет жить»:

X = ж >  0 :

У^ жр = dw, w Е OD > , PEPw и функцию, порождающую потенциальное векторное поле G (ж):

/ е (^{х )}

Ф

^(ж)=Е I е Е^Е 0

т _е (г) dz.

Основное свойство этой функции заключается в том, что

V Ф(ж) = G (ж).

Будем считать, что число пользователей транспортной сети большое:

dw := dw • N, N » 1, w E OD, но в функциях затрат это учитывается:

Т е (fe) := T _e (fe/N ) .

Таким образом, далее под d _w , ж, f будем понимать соответствующие прошкалированные (по N ) величины [4].

Выберем корреспонденцию w E OD и рассмотрим пользователя транспортной сетью, соответствующего этой корреспонденции. Стратегией пользователя является выбор одного из возможных путей следования р E Pw. Будем считать, что пользователь мало что знает об устройстве транспортной системы и о формировании своих затрат. Все, что доступ- но пользователю на шаге к + 1, — это история затрат на разных путях, соответствующих

{'; = g (ж' ) }„„ . }‘ _₁

его корреспонденции, на всех предыдущих шагах

. Для простоты

рассуждений мы не зашумляем эту информацию, считая, что доступны точные значения имевших место затрат. Все последующие рассуждения (ввиду общности выбранной в разделе 2) можно обобщить и на случай зашумленных данных (детали мы вынуждены здесь опустить).

Допуская, что 0 6 {Zp} 6 М могут выбираться враждебно, пользователь стремится действовать оптимальным образом, то есть так, как предписывает стратегия из примера 3 (с г = р, п = \ P _W | ). Заметим, что при некоторых дополнительных оговорках (см. п. 5.4 [1]) случайный выбор пути (согласно примеру 3) может быть осуществлен за время O ( | Е | ), что не зависит от п, которое может быть намного больше (например, для манхетенской сети, см. п. 5.4 [1]).

Представим себе, что остальные пользователи ведут себя аналогичным образом, но независимо (в вероятностном плане) друг от друга. Тогда в пределе N ^ то такая стохасти- ческая марковская динамика в дискретном времени вырождается в детерминированную динамику в дискретном времени [16], описываемую итерационным процессом из примера 2 с j =w, Z3 = {жр}реРш, п = |pw|, а, = М-1 2lnn,/N,

N Regret _N 6 max a

3=1,...,m •

' 3

¹ ( R ² +— М ² N max a² ) ,

\        2         j=1,...,m

для задачи не онлайн оптимизации:

Ф (ж) ^ min, xEX

f k (ж) = Ф (ж) , ж^ = N ^ ж ^к ,  Ф * = Ф (ж * ) ,

N к=1

Ф (ж^) - Ф * 6 Regret _N 6

max { ln п ₃ }

М    j=1,...,m       ³

NN /2 min { Inn у j=1,...,m

m       \

E d 3 + 1) .

3 =1       /

Решение задачи (4) иногда называют равновесием Нэша(–Вардропа) в описанной популяционной игре [4, 17], соответствующей модели Бэкмана равновесного распределения потоков по путям [2]. Для простоты формулировок будем далее считать, что решение единственно.

Введем теперь схожий процесс (совпадающий с описанным ранее в пределе N ^ то ): дискретный аналог имитационной логит-динамики с произвольным параметром а >  0, популярной в эволюционной теории игр [4]. Пусть отрезок времени [0, Т ] разбит на Т N ^ 1 одинаковых отрезков, соответствующих шагам. На каждом шаге к = 1,...,TN каждый пользователь корреспонденции j = w Е OD независимо от всех остальных пользователей с вероятностью N ^-1 принимает решение выбрать потенциально новую стратегию (маршрут следования) согласно распределению вероятностей г Е P j (в действительности, тут требуются некоторые оговорки на случай, когда x ^k = 0, мы опускаем здесь эти детали, за подробностями отсылаем к монографии [4]):

Р^¹ =

x ^k exp ( — aG _i (x ^k ))

Z xk exp (—aGi (xk)), ip а с вероятностью 1 — N-1 — использовать стратегию предыдущего шага. Аналогично действуют пользователи, принадлежащие другим корреспонденциям: j = 1, ...,m. Тогда в пределе N ^ то эта динамика превратится на отрезке [0, Т] в имитационную логит-динамику в непрерывном времени [4, 16], в которой с каждым пользователем связан свой (независимый) пуассоновский процесс с интенсивностью 1. В моменты скачков процесса пользователь принимает решение о потенциальной смене маршрута следования согласно распределению вероятностей г Е Pj, j = 1, ...,m:

( _t ) = X i (t) exp ( — aGi (x (t))) ^{P i} Z x i (t) exp ( — aGi (x (t)))^.

i ^ P i

При T ^ то описанный эргодический марковский процесс выходит на стационарную вероятностную меру [4]:

~ exp (—N • (Ф (х) + о (1))) , которая при N ^ то экспоненциально концентрируется в окрестности решения задачи (4).

Если описанные предельные переходы выполнить в обратном порядке: сначала N ^ то , потом Т ^ то , то марковский процесс, отвечающий имитационной логит-динамике, выродится в СОДУ г Е P j , j = 1, ...,m:

dx _i (t)         X i (t)exp( — aG _i (x (t)))

dt ^j Z x _l (t) exp ( — aG _l (x (t))) i ^ P j

-

X i .

Эта динамика (на внутренности инвариантного относительной данной динамики множества X ) имеет глобальным аттрактором неподвижную точку, определяемую как решение задачи (4). Более того, СОДУ (5) имеет функцию Ляпунова Ф (x) [4] (это общий факт: функционал Санова является функционалом Больцмана [18]), причем [5]

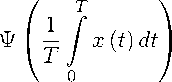
1 m

^{— Ф} * ⁶ ат ^' 2 ^;.

j=i

Заметим также, что СОДУ (5) можно понимать как непрерывный аналог (см., например, [19]) примера 2.

Работа выполнена при финансовой поддержке РФФИ (коды проектов 13-01-12007-офи_м, 15-31-20571 мол_а_вед, 15-31-70001 мол_а_мос). Исследования первого автора, связанные с п. 2, выполнены в ИППИ РАН за счет гранта Российского научного фонда (проект № 14-50-00150).