О связи между степенью суммируемости почти-периодических функций и коэффициентов Фурье

Известно [1], что если {cn} — коэффициентьi Фурье функции f (x) С L2 по любой ортонормированной системе {^(x)}, то имеет место неравенство

∞

Е w2

n =1

b j |f (x)|2 dx.

a

Если рассматриваемая система, полна, то это неравенство превращается в равенство, т. е. если существует последовательность чисел {cn}, для которых P |c_n|²< то, то найдется функция f (x) С L2, для которой эти числа будут коэффициентами Фурье и

b j If (x)|2 a

∞ dx = ElCnl2.

n =1

Если функция f (x) С L p (p >  1), то что можно сказать об ее коэффициентах Фурье? II наоборот, если P |c_n|p < то. то существует ли функция. имеющая {cn} своими коэффициентами Фурье, и какова степень ее суммируемости?

Ответы на. эти вопросы для случая тригонометрической системы даются теоремой Хаусдорфа. — Юнга. (см. [1, с. 211]), а. для общей ортогональной системы — теоремой Рисса (см. [1, с. 211]).

Пэли [2] доказал, что если f (x) С Lp, 1 < p 6 2, {c n } — ее коэффициенты Фурье по ортонормированной системе {^_n(x)} нa [a, b], |д_п(x) | 6 M, n = 1, 2,..., a 6 x 6 b, to

∞             1/p e ыр np-2

6 Ap

b j If Ip dx >

1 /p

a

где Y1, Y2, • • •, Yn, • • • ^{— 4}исла |ci|, |c2|,..., |cn|,..., расположенные в порядке убывания и Ap зависит только от p и M. Если же p > 2 11 c 1 ,c₂ , • • •, cn, • • • — последовательность чисел, для которой

∞

X ЫРnp-2 < +^, n=1

то существует функция f (x) G Lp(a, b), для кото рой числа cn являются коэффициентами Фурье по системе {^n (x)} и имеет место

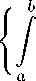
1/p          ∞              1/p

6 Bp ЁЫ”np-2   ,

где Bp зависит только от p и M.

В этой работе получены результаты, которые являются аналогами теоремы Пэли для почти-периодических в смысле Безиковича и Степанова функций при p > 2 по произвольной тригонометрической системе {exp(iAkx)}.

Определения и свойства почти-периодических в смысле Безиковича и Степанова функций можно найти в [3].

ОПРЕДЕЛЕНИЕ 1. Функцию f(x) называют Bp-почти-периодической, p > 1, или почти-периодической в смысле Безиковича, если |f (x)|p интегрируем на любом конечном отрезке,

D B p ^{f(x)} = ( Tim^T / ^|f(x)|p^dx )    < ^ro,

и существует ряд вида

СЮ

Pn(x) = У^ ck exp(iAkx), k=-∞ для последовательности прямоугольных сумм {Pn (x)} которого выполняется nlim^ DBp{f(x) - Pn(x)} = 0.

Пространство функций, удовлетворяющих всем условиям определения 1, принято называть Bp-пространством, или пространством Безиковича, в котором за норму функции f (x) G Bp (p > 1) принимается величина kf(x)kBp = ( lim      / |f (x)|p dx)    < ”•

T юго 2T JT

Если f (x) G Bp. то миожество Л{Ак}. для которых

T

Ak

-im —   f (x)exp(-iAkx)

dx = 0,

T юго 2T

-T счетно и принято их называть спектром (показателями Фурье) Bp-почти-периодической (руиктпш f (x). a mi 1С,та {Ak} — KO9<|><|>iiniieiirbi Фурье (руиктпш f (x) G Bp. Таким образом. каждой <|>упкппи f(x) G Bp с помотпьто ее спектра Л{Ак} и коэсрсритщеитов {Ak} ставится в соответствие ряд f (x) ~ X Ak exp(iAkx), k который называется рядом Фурье функции f (x) G Bp.

Справедливо следующее утверждение.

Теорема 1. Пусть задан тригонометрический ряд

n

X Ak exp(iAkx),

k =1

где Л{Ак} — произвольное счетное множество действительных чисел. Если при некотором p >  2

∞

Стр = X |An|p np^-2 < то,                              (2)

n=1

то в пространстве Bp найдется функция f (x). для которой ряд (1) будет ее рядом Фурье и имеет место

Db p {f (x)} 6 C -                                      (3)

Заметим, что так как из условия (2) вытекает сходимость ряда РП=1 | Ak|², то на основании аналога теоремы Рисса — Фишера (см. [3, с. 252]) в пространстве Bp найдется функция f (x). для которой ряд (1) будет се рядом Фурье.

Сначала нам необходимо доказать справедливость следующего неравенства

DBp {Pn(x)} 6 n1/2-1/pDB2 {Pn(x)} , p> 2.(4)

Известно, что n

Pn(x) = Mt Pn(x + t) X exp(-iAkt) = 11m      [ Pn(x + t) X exp(-iAkt) dt,

Tмж 2T / k=1                          -Tk=1

следовательно,

Тогда

max |Pn(x)| 6 n¹/² (m | |Pn(x)|² j) / .

TT

[ ^|pn^(x)|p ^dx 6 ^{max |p}n^(x)|P-2 Дф [ ^|pn^(x)|2 ^dx

2T                         x                2T

- T                                 - T

T

6 np^-2 ( M { ^|pn^(x)|2 ^}) P^ 21T У ^|Pn^(x)|2 ^dx-

- T

После перехода к пределу по T ^ то получим неравенство (4).

C ДОКАЗАТЕЛЬ(ЙТВО ТЕОРЕМЫ 1. При всяком натуральном N рассмотрим сумму

2N+1                  N

S2N+i (x) = X Ak exp(iAkx) = ХЛп’ k=1                 n=1

где

2 n+1— 1

An = An(x) = У^ A v exp(iX v x).

v =2 ⁿ

В силу почти-периодичности функции имеем

T

2T у S 2 N+1 (x)

-T

dx

£/ E An dx-

- T n =1

Отсюда при r = [p] + 1. R = r^r^-) 11 5_V = |A_v|^p/r. получаем

T

2T У ^N+1 (x)|p dx =

-T

T

N

p

p

—  V A„ dx

2T J        ^v

-T

T

v =1

TN         r

6 2T   X ^0 dx

-T   v=1

N

Nr

- ЦУ 5 dx =

2T J )        \

-T v=1

N NT

2TE---E i    ■■■5vrdx v1 =1   vr =1-T

NNT

X - X 2T   n e^-4ij-¹¹ dx.

v 1 = 1    v r =1     _— t 1 6 i 6 j 6 r

После применения неравенства Гёльдера получим

T                  N N               T

2T  IS 2 N+1 (x)|^p dx 6 Е^Х П   TrOO S V/ ² dx

-T                     vi = 1    Vr = 1 16i6j6r

N N               T

= X...X П   2T/I Avi A„, 12 dx, v1=1    Vr=1 16i6j6r w r = [p] + L R = rrfc-a

В правой части (6), применяя неравенство Гёльдера с показателями a = (p + 2)/2 и a = (p + 2) /р. находим

T

1                     p .

2T J ^|A^^Av 1² dx 6

- T

T

- T

²· ^p T

IA-C dx}' Xf

|A_V | ² dx

2p p+2 2

После перехода к пределу, при T ^ то, будем иметь

,.       1

lim тюго 2T

T

p

A-Av |² dx

T

lim

T→∞

T                   2·p                  T

{ 2T/^ ..}'"  т.,{ х ^f

p+2

|A_V | ² dx

2p p+2 2

или

2 ·p                                           2 ·p

M { |A^Av|² } 6 (m { |A^|Ч }) ^{pa 2} • (m { |Av|p^ }) ^p+2'² .

Применяя к правой части (7) неравенство (4), получим, что

M { AAv|p } 6 2(р+1)(1/2-1/а)Yy22(v+1(1/2-1/a0’yV/2 = 2(p+1)(p/4-1/a) (M { А|2})p • 2(v+1)(p/4-1/a0’ (M {|Av|2})p , где

/2v+1-1\

Y_v = 2^(v+1)(p/2-1) ( M ^{|A_v|^{2}) 2} = 2^(v+1)(p/2-1) I X |Ak|² )

\ k=2 ^v

Так как Л = 1 — 1, то из соотношения (8) вытекает, что а0

M ^{|A_MAv|Р^/2} 6 2^-k^-vl⁽¹/ 2 ^-V^a)■ yV^/2 .

Благодаря (6), (7) и (9) имеем

p

.

NN1

м {|S2n+, (x)ip}6 x-X n ! ■² yV/² з^-^^1-'-"¹/^2-1/»’}R. v1 = 1     vr =1 1 6 i 6 j 6 r

Далее, поступая так же как и в работе [4], находим, что

N           N             2n+1 -1

M{ | S 2 N+i ( x ) | p} 6 Cp^L Yn = CpX2 ' I E IAk1²1

Покажем теперь, что из условия (2) вытекает сходимость ряда.

го               2n+1-1\Р

^X 2"^(p/2-1)f X IAk1²)

Сходимость ряда. (И) эквивалентна, сходимости ряда.

N            гоР

X np/2-2 Xi Ak 12.

n =1

(И)

Используя неравенство (см. [5, с. 308]), ∞∞

X n-c Xdk  6 AX"-c (ndn)‘, n=1      k=nn при c = 2 — p/2 < 1. 5 = p/2 > 1. dn = |An|2. получаем го                го          p/2

X n-(2-P/2) X I Aki2     6 A X I An|P"P-2- n=1           k=nn

Следовательно, в силу условия (2)

∞

M {|S2N+1 (x)ip} 6 Cp X |AnIp np-2 < x ■ n=1

Из сходимости ряда х               2n+1-1       pP/2

X И"*/2-»! X |AkH вытекает, что для любых m. n (m > n)

m              2k+1-1\

X 2k(p/2-1)   X |Av|2^ о k=n          \ v=2k/ при m ^ to, n ^ то, и так как неравенство (10) верно для любого полинома и, в частности. для S2m+i (x) — S2n+i (x) то при m ^ то. n ^ то

Db _p {S 2 m+1 (x) — S 2 n+1 (x)} ^ 0.

В силу полноты пространства найдется функция f (x) G Bp, для которой при n ^ то

DBp {f (x) — S 2 n+1 (x)} ^ 0

и, следовательно, для нее будет верно неравенство (3). B

ЗАМЕЧАНИЕ. В теореме 1 условие (2) можно заменить более слабым условием p/2

2 ⁿ⁺¹- 1         ^p/

X |Ak|² )     < то.

k =2 ⁿ

ОПРЕДЕЛЕНИЕ 2. Под Sp-пространством, или пространством почти-периодических функций Степанова, понимается совокупность функций, для которых

Dsp {f (x)} = sup

x

< ∞ ,

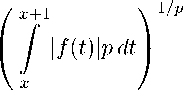
и можно указать последовательность тригонометрических сумм {Pn(x)}

n

Pn (x) = ^Ck exp(i^k x) k =1

таких, что

lim DSp {f (x) — Pn (x)} = 0. n →∞

Теорема 2. Пусть задан ряд (1), где Л {Ak} — последовательность чисел, удовлетворяющая при некотором a >  0 для всех n

An +i — An > a.

Если выполнено условие

∞

Стр = X |An|^pn^p-2< то, n =1

то в пространстве Sp (p > 2) найдется функция f (x), для которой {Ak} будут ее коэффициентами Фурье и имеет место оценка

Ds p {f (x)} 6 C p ^V^P.

C Доказательство теоремы 2. Покажем вначале, что для любого полинома вида (12) при выполнении условия (13) и p >  2 справедливо неравенство

1-1

D S p {Pn(x)} 6 An ^{2 p}

■ n \ 1/ 2

Ei cki2

. k=1 /

Действительно, так как u+ 1

2 / |Pn(x)l^p

dx 6

u+ 1

J (¹ -|x

— u|) |P_n(x)|^p dx

u-

u-

max |Pn x

u + -^(x)|p-2 / ^{(1 — |x}

— u|) |Pn(x)|² dx,

то на. основании неравенства. (5) получим, что p-2

D S p {Pn (x)} 6 n '2

MM {|Pn(x)|²})

p-2 2

u + 2

у (i — |x

— u|) |P_n(x)|² dx.

u-

В работе [3] установлено, что u+-

J (1 — |x

u

— u|) |Pn(x)|² dx 6 A XX |c k |² = AM {|Pn(x)|²} . k =1

Следовательно,

D S p {Pn(x)} 6 Anp^-

(m {|Pn(x)|²})p/² ,

что дает неравенство (14).

Используя тот же метод, что и при доказательстве теоремы 1, найдем D s p {P_n(x)} 6

1 /p

C _p σ p

S p                              B