О свойствах решений краевой задачи, моделирующей термокапиллярное течение

Двумерное течение вязкой теплопроводной жидкости описывается системой урав нений ut + (г1 • V )и +— Vp = v Агг,   dh" u = 0,

(0.1)

ρ

9t + гг • V9 = хА9, где u = (u(x,y,t),v(x,y,t)) - вектор скорости, p(x,y,t) - дав.теине. 9(x,y,t) - температура суть искомые величины; р > 0, v > 0, х > 0 - плотность, кинематическая вязкость и температуропроводность жидкости, соответственно, являются заданными постоянными. Жидкость находится на твердой неподвижной стенке у = 0 и контактирует с пассивным газом через свободную границу у = l(x, t) > 0. На этой границе поверхностное натяжение линейно зависит от температуры а(9) = а0 — ж9 [1] с постоянными ст0 > 0, ж > 0, которые достаточно надежно определяются из эксперимента [2] для конкретных жидких сред.

Сделаем следующие предположения: 1) число Вебера (или обратное ему капиллярное число) We = а 0 h/ ( pvx ) ^ 1 ( ^ 1), тогда [1,3] свободная граница есть линия у = l = const >  0. параллельная твердой стенке у = 0. h = max l ( x, 0) -характерная толщина слоя жидкости; 2) поле скоростей имеет специальный вид:

u = ( w ( у, t ) х, v ( у, t )). Такое поле скоростей впервые было предложено в работе [4] для описания натекания чисто вязкой жидкости из бесконечности на твердую стенку у = 0 с условием прилипания на ней. Для стационарных течений в канале или трубке с твердыми стенками такое поле скоростей использовалось в работе [5]; 3) поле температур квадратично по х; 6 = a ( у, t ) х ² + b ( у, t ). Если на твердой стенке задана температура, 6 _о( х, t ) = 6 ( x,y,t ) = a _о( t ) х ² + b _о( t ). то при a _о( t ) >  0 она, в точке х = 0 имеет минимальное значение, а при a _о( t ) <  0 - максимальное. Поэтому в настоящей работе будут изучаться двумерные течения специального вида, возникающие вблизи точки экстремума, температуры на твердой стенке.

При подстановке стационарного поля скоростей и температур в уравнения (0.1) и анализа на совместность придем к системе vw" = vw' + w2 — f, v' + w = 0,

(0,2)

Xa" = va' — 2 wa, xb" = vb' — 2 xa, где штрих означает дифференцирование по у, 0 < у < I. Граничные условия для системы (0.2) таковы:

w (0) = v (0) = 0, a (0) = a 0, b (0) = b 0, v (l) = 0, w' (l) = — 2$ a (l), ka! (l) + Ya (l) = 0,

(0,3)

kb' ( l ) + Yb ( l ) = Y6 о + q о , где a о, b о - заданные постоянные, k >  0 - коэффициент теплопроводности жидкости, Y - коэффициент межфазного взаимодействия, 6 ₀ - постоянная температура газа вне жидкости, q о - заданный постоянный поток тепла. Давление в жидкости определяется по формуле

- p = vv' — - v ² p

^— 2 ^fx + ^d о

(0,4)

с постоянной d 0. Таким образом, постоянная f представляет собой « градиент » давления вдоль канала, и он должен определяться вместе с решением задачи (0.2), (0.3)

т.е. поставленная задача, является обратной. Заметим также, что задача, на функцию b ( у ) отделяется п основной будет краевая задача, нахождения функций w ( у ). v ( у ). a ( у ) II постояшюй f. В свою очередь. после исключения функции v ( у ) из второго уравнения системы (0.2)

y v (у) = — j w (z) dz задача сводится к обратной для w(у), a(у) и f. Далее считаем, безразмерные величины

W ( 5 ) = 2Г w ( у ) , A ( 5 ) = aM,F = -4- f,( = у, P = —, 11 =

X                   a 0         x²           l X

(0,5)

что a 0 = 0 и введем

, в = Yl, („.у ρνχ k

тогда, упомянутая выше обратная задача, примет вид

ξ

W" +   W' I W ( z ) dz = 1 (^I W ² —

F ) ,

ξ

A" + ^ Ы ' У W ( г ) dz = 2^ I AW, 0 <(< 1 ,

(0,7)

W (0) = 0 , A (0) = 1 ,                              (0.8)

W ‘ (1) = - 2 A (1) ,  A’ (1) + B A (1) = 0 ,                     (0.9)

IW ( г ) dz = 0 .                              (0.10)

Последнее интегральное условие есть следствие (0.5) и равенства v ( l ) = 0.

Замечание 1. Полученная краевая задача (0.7) - (0.10) является нелинейной, ин-тегродифференциальной и представляет новую математическую модель термокапиллярного двумерного движения в слое. Как правило, в практических приложениях [1,3] число Марангони М невелико, поэтому исследование указанной задачи (и ее нестационарного аналога, см. п. 2) методом возмущений по данному параметру является актуальной задачей. При этом будут определены: необходимый для возникновения движения градиент давления вдоль слоя, поле скоростей и температур.

1.    Ползущие течения - модель Стокса

Число Марангони М в уравнениях (0.7) - (0.10) входит сомножителем при нелинейных слагаемых и играет роль числа Рейнольдса [6]. При стремлении числа Рейнольдса к нулю система уравнений вязкой жидкости становится линейной и называется системой Стокса, или моделью Стокса. Она описывает ползущие или медленные течения. В нашем случае при | М | ^ 1 решение задачи (0.7)—(0.10) ищется в виде

W ( ( ) = W ⁽⁰⁾( ( ) + A W ⁽¹⁾( ( ) + ..., A ( ( ) = A ⁽⁰⁾( ( ) + AI A ⁽¹⁾( ( ) + ...,

F = F ⁽⁰⁾₊у F ⁽¹⁾ + ....                           ^(М)

Для нулевого приближения легко находим

W ⁽⁰⁾( с Щ^ ( с ^- 2 е ²) , A ⁽⁰⁾( с ) = 1 ^- ^ с F ⁽⁰⁾ = АД .    (1.2)

Краевая задача для первого приближения будет уже неоднородной и с учетом

(1.2) примет вид

A ⁽¹⁾ ‘‘

w ⁽¹⁾ ‘‘ ₌ _F 2 ₊ —¹— W        Р +2Р(1 + В)²

- ³ е ² + ² е +

1 +

(2 е * - 2 е 3 + е А ,

1 + В

(5 е ³ -

з е ²) , 0 < е <  1 ,

(1.3)

W ⁽¹⁾(0) = 0 ,   A ⁽¹⁾(0) = 0 ,

W ⁽¹⁾ ‘ (1) = - 2 A ⁽¹⁾(1) ,   A ⁽¹⁾ ‘ (1) + B A ⁽¹⁾(1) = 0 ,

IW ⁽¹⁾( z ) dz = 0 , 0

(1.4)

т.е. изменилось лишь условие для функции A ⁽¹⁾( е ) при е = 0. Интегрируя уравнение (1.3) и удовлетворяя граничным условиям (1.4), после некоторых вычислений получим представления для первого приближения

^{W (1)}( С ) = -— ; ² + _{12ор(1 + в)} 2 (3 { ⁶ - 6 { ^{5 + 5} { 4 )⁺ ^

A °^{( С} )   12(1 +В)

- 3 С 4 + 4 С ² + i+в ( С ⁵ - С 4 )

в(4 +В) _С 12(1 + В)^{3 С} ,

(В5)

1     ⁽1 - 2В 19 )    - ⁽¹⁾       1     ⁽1 - 2В,  5

12(1 + В)²   1 + В ⁺ 70В / , "^ = 4(1 + В)²   1 + В ⁺ 14В

2.    Нестационарная модель медленных движений и ее анализ

В этом случае все функции зависят от времени t и вместо краевой задачи (0.7) -(0.10) возникает начально-краевая задача ( т = xl- 2 1 ~ безразмерное время)

W t + М WW ²

-

ξ

W^ I W ( z, т ) dz ) = B W _€€ + - ( т ) ,

ξ

А т + М ^2 AW - A^ W ( z, т ) dz^ = A^,  0 < С <  1 ,

(2.1)

W (0 ,т ) = 0, A (0 ,т ) = A i( т),(2.2)

W§ (1 ,т ) = - 2 A (1 ,т), A§ (1 ,т) + BA (1 ,т ) = 0,(2.3)

I W(z, т) dz = 0,(2.4)

W ( С, 0) = W o ( С ) , A ( С, 0) = A o ( С ) .                      U-Z

Равенства (2.5) представляют собой начальные условия, для гладких решений должны быть выполнены условия согласования

W о (0) = 0 ,  A i (0) = A o (0) ,  W о § (1) = - 2 A o (1) ,

(2.6)

^A о § ^{(1) +} B A о ⁽¹⁾ = ⁰ ,

W o ( z ) dz = 0 .

В уравнениях (2.1) число Марангони М определяется равенством (0.6), где а ₀ = sup |A 1 ( т ) | для ограниченной по физ:шескому смыслу функции A 1 ( т ), так что здесь τ > 0

М >  0.

Ограничимся нулевым по числу Марангони решением задачи (2.1) - (2.6). При этом функции W ( С,т ), A ( С,т ), F ( т ) есть решение линейной системы

W t = P W _€€ + F ( т ) ,   A t = A §§ ,  0 < С <  1 ,

(2.7)

с условиями (2.2) - (2.6). Указанная обратная начально-краевая задача, может быть решена методом разделения переменных: классическим для A(С,т) и специальным, как это было предложено в работах [7,8] для W(С,т), F(т). Получающиеся ряды имеют довольно громоздкий вид и медленно сходятся для имеющих разрывы первого рода функций W0( Z), А о( Z). Кроме тог о, функция А 1 (т), с помощью которой можно управлять движением жидкости, также может иметь разрывы первого рода. Поэтому будем решать задачу методом преобразования Лапласа (условия его применения см., например, в [9]).

Пусть

∞

W ( Z,Z )= /

∞

e ^Zt W ( Z,T ) dT,

А ( Z,Z ) = /

e ^Zt A ( Z,T ) dT,

∞

^{F ( Z} ) - у

e ^Zt F ( т ) dT

есть преобразования Лапласа W ( Z,T ), А ( Z,T ), F ( т ). Функции W ( Z, Z ), А ( Z, Z ) F ( Z ) суть решения краевой задачи для ОДУ:

л1

W ее ^— д W ^{- —} р [ ^F(Z ) + W о ^{( Z )]} .

(2.8)

/X/X

^А ее — Л ^— -А о ( ^Z ) .  О < ^ <  1;

/X/X

W (О ,Z ) —0 ,  А (О ,Z ) — А 1 ( С );

W e (1 , Z ) — — 2 А (1 , Z ) , А е (1 , Z ) + в А (1 , Z ) — 0;

J W U ) d ^{Z — 0} .

Задача для функции А ( Z, Z ) отделяется и

ξ

А ( Z,Z )— C 1 ( Z )shV ZZ + А 1 ( Z ) chV ZZ — ^д. I ^shV Z ( Z — 2 ) А о ( z ) dz, (2.10) 0

C 1 ( Z ) —

VZ ch v+ + Bsh VZ

-

Ц\ ch ^V Z (1 — z ) + ^ sh V X (1 — z )^] А 0 ( z ) dz— Z sh V Z + Bch V Z ) м z )} .

/\                 /X

Функции F ( Z ), W ( Z,Z ) найдутся из первого уравнения (2.8) и трех условий (2.9) для

/X

W ( Z,Z ):

/X

F ( Z )

1 — УЧ ^{- 1} th V Z i ^-

1 ξ

{ V Z b ^{3 1} У ^sh y Z F¹ ( Z — z ) W o ( z ) dzdZ +

+-

-

^ch vy " [У ch V Z F1 (1

ch \ Z

-

z ) W о ( z ) dz — 2P.4(1 ,Z ) У

1 W ( Z, Z ) — C 2 ( Z ) sh V*^-Z + (1 — ch Vv- z) F A)

PC

ξ

I sh У Z Г ¹ ( Z — z ) W o ( z ) dz, 0

(2.11)

с 2 ( z ) = 1th ДЛ¹ f ( z ) — , 2—_I к . A (1 ,? )+

?                 ch у ?

+[ ch \/ ? P ^{- 1} (1 — z ) W_o ( z ) dz.

^V ch ....0                            ^0M

В формулах (2.11) A (1 , ? ) есть значение прав ой части (2.10) при С = 1

Предположим, что существует предел lim A 1(т) = 1 и A 1(т), A1 (т) являются τ→∞ оригиналами, тогда [9] lim A A 1(?) = 1. Используя асимптотические разложения ги-ζ→0

перболических функций при малых значениях аргумента, из полученных формул (2.10), (2.11) можно вывести равенства lim zA (С,? ) = A 0( С), lim ?F (Z ) = F0, lim W (С, ? ) = W 0( С), ζ→0                     ζ→0                ζ→0

(2.12)

т.е. при t ^ то решение задачи (2.7), (2.2) - (2.5) стремится к стационарному решению (1.2). Конечно, формулы (2.10), (2.11) дают решение в квадратурах для изображений по Лапласу и в случае, когда функция A 1 ( т ) имеет конечное число разрывов первого рода и не имеет предела при т ^ то . Пример численного обращения преобразования Лапласа приведен в следующем пункте.

3.    Термокапиллярное движение первоначально покоящейся жидкости

Считаем, что в начальный момент времени жидкость находилась в покое ( W ₀( С ) = 0. С Л [0 , 1])- и фуикция A ₀( С ) — 0. С Л [0 , 1]- При т >  0 А >  0) A 1( т ) >  0 п возникает термокапиллярное движение. Для выполнения условий согласования (2.6) можно считать, что A 1(0) = 0, хотя это и не обязательно. В этом случае вид решения в образах по Лапласу (2.10), (2.11) существенно упрощается,

/X

A ( С,? ) =

^[ V? ^ch V? ^{(1 — С} ) + В sh V? ^{(1 — С )] A} 1 ⁽ ? )

? ch Д ? + В sh V ?

«.,,,                2Р V? (ch vVp ^{- 1} — 1) A 1( ? )

(3.1)

F ( ? ) — -------------------------------------------------,        ■--------- - ---------,        —,

( V? ch V ? + в sh V ? )(ch v^/ ? P ^{- 1} — _x      sh v^/ ? P ^{- 1} )

iW( c,? ) — [¹ th J ? p ^{- 1} . F ( ? )-- _;     ²^ ^A —--------- ] sh J ? p ^{- 1} с +

^,       ?                ch V Z T ^{- 1} ( V? ch V? +Bsh V? )

+ (1 — ch Z ? p ^{- 1} c ) FA.

Численное обращение преобразования Лапласа a-i∞ g (С,т) —А [ G (С,?) e^ d?,

(3.2)

2 ni a+i∞ где G(£, £) последовательно есть правые части (3.1), a. g = A(^,т), g = F(т) g = W(^,т), выполнялось при помощи квадратурной формулы наивысшей точности, построенной для интеграла Римана - Меллина (3.2).

Моделировался процесс возникновения термокапиллярного движения в слое трансформаторного масла толщиной l = 10 ^{- 7} м и физическим и параметрами р = 0 , 86 • 103 кг/м³; v = 18 , 49 • 10 " ⁶ м² с •; х = 1 , 21 • 10 " ⁵ м² с •; к = 0 , 63519 • 10 " ⁴ к г • а /с 3; ж = 0 , 0022 Н/м • К. При характерном перепаде температур вдоль свободной границы △ 9* = a 0 l = 10 К получим для числа. Марангони М = 1 , 143 • 10 ^{_ 2} <  1, а. число Прандтля Р = 1 , 53. Расчеты проводились по формулам (3.1), (3.2) для числа Био В = 2. На рис. 1 - 5 приведены графики только функций F ( т ), W ( £, т ), V ( £,т ). Для вычисления последней использовалась формула (0.5) в безразмерном виде. Функция A 1 ( т ) выбирала св в виде A 1 ( т ) = 1 — sin(0 , 1 т ) exp( — 0 , 01 т ) 11 A 1( т ) = 2sin(0 , 1 т ). В первом случае есть сходимость к стационарному режиму (сплошная линия), а во втором такой сходимости нет, что согласуется с теоретическими выводами. Таким образом, выбирая тот или иной тепловой режим на твердой стенке, можно управлять движением жидкости внутри слоя.

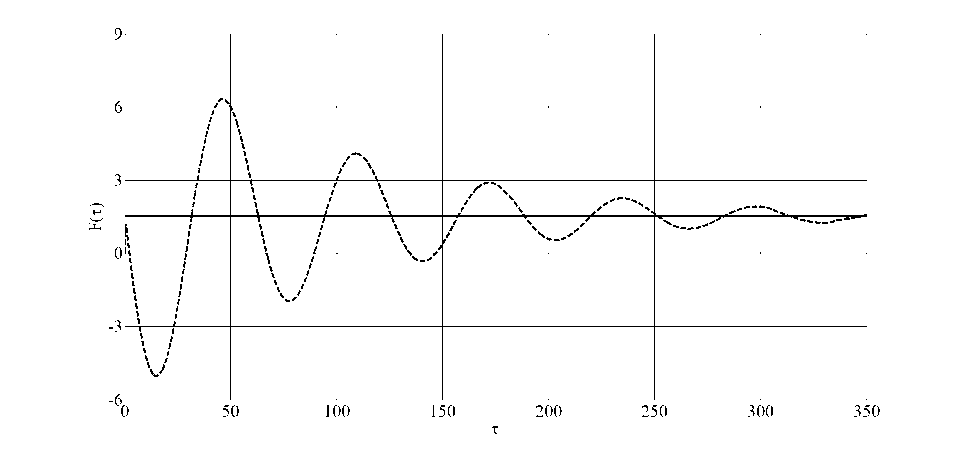
Рис. 1. Поведение функции F ( т ) при A 1( т ) = 1 — sin(0 , 1 т ) exp( — 0 , 01 т )

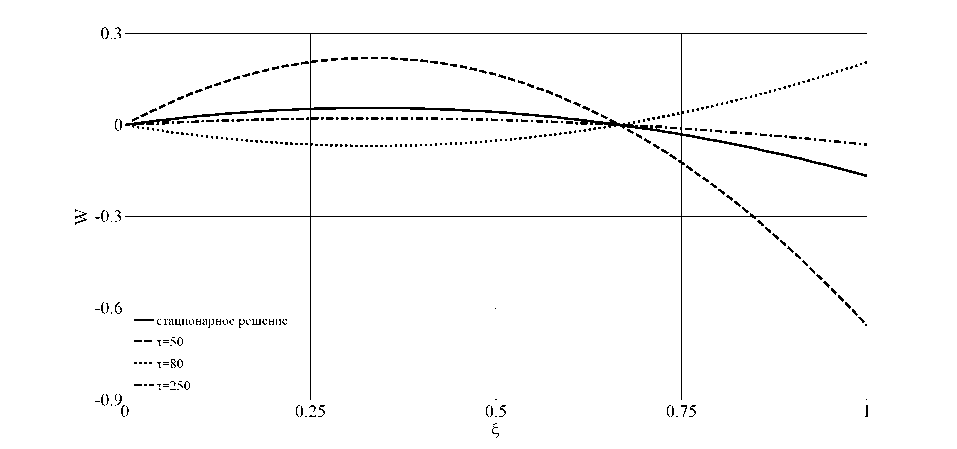
Рис. 2. Поведение функции W ( ^,т ) при A 1 ( т ) = 1 — sin(0 , 1 т ) exp( — 0 , 01 т )

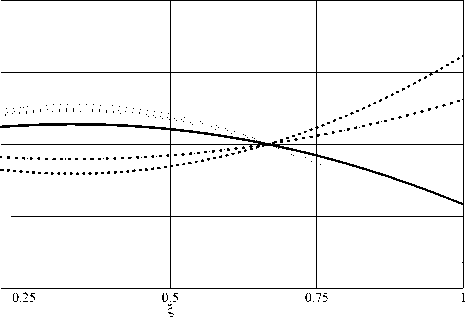
Рис. 3. Поведение функции W ( ^,т ) при A 1( т ) = 2sin(0 , 1 т )

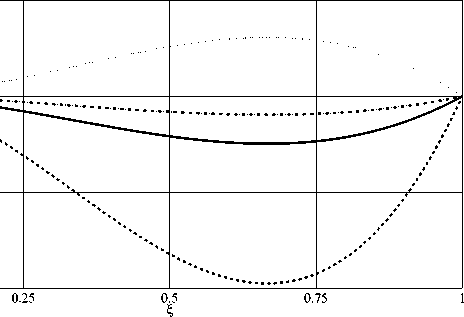
Рис. 4. Поведение функции V (ф т ) при A 1( т ) = 1 — sin(0 , 1 т )exp( — 0 , 01 т )

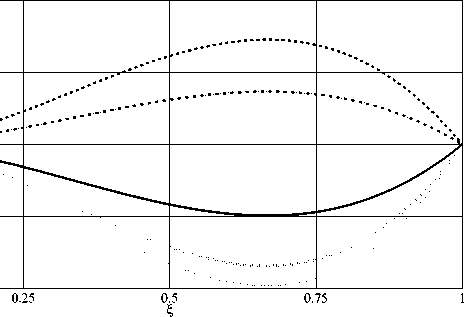
Рис. 5. Поведение функции V (ф т ) при A 1( т ) = 2sin(0 , 1 т )

Замечание 2. Поле давлений может быть найдено из формулы (0.4), где для нестационарного случая в правую часть необходимо добавить —v t . Функция b ( у ) вычисляется по известной a ( у ) из решения краевой задачи (0.2), (0.3), где надо вычеркнуть нелинейное слагаемое vb'. Тем самым и поле температур будет полностью восстановлено для стационарного течения. Для нестационарного движения уравнение для

b ( y, t ) имеет вид b _t = xb _yy + 2 х° , соответствующая начально-краевая задача также решается методом преобразования Лапласа.

Заключение

Методом возмущений по малому параметру (числу Марангони) найдено решение краевой (и начально-краевой) задачи, возникающей при математическом моделировании термокапиллярного движения жидкости вблизи точки экстремума температуры на стенке. Получено аналитическое решение для стационарного течения. Для нестационарного движения решение найдено в виде квадратур в пространстве изображений по Лапласу. Даны достаточные условия выхода решения на стационарный режим с ростом времени. Методом численного обращения преобразования Лапласа решена задача о возникновении термокапиллярного движения при различных способах задания температуры на стенке в слое трансформаторного масла.