О третьих формах конъюнкции и дизъюнкции в логиках с векторной семантикой

В работах автора (см., например [1, 2]) обсуждались вопросы логического формализма, построенного на основе векторной семантики типа V TF , когда истинность суждения a имеет векторное представление:

|| a ||= 〈 a ⁺; a ^- 〉 , (1) где позитивный компонент a + характеризует степень уверенности, что суждение истинно, а негативный a ^- – что ложно; a ⁺; a ^- ∈ [0,1].

Такой взгляд оправдывался тем, что во многих предметных областях вывод об истинности или ложности того или иного суждения приходится делать на основе информации, поступающей из различных не зависящих друг от друга источников. Сведения от них могут согласовываться, а могут противоречить друг другу. Источники могут иметь разную степень доверия, что должно отражаться соответствующим формализмом. Обычный подход к формализации неточного знания, основанный на скалярных показателях вероятно-сти/уверенности/истинности (см., например [3-5]), не всегда адекватен, так как основан на предположении, что дефицит доверия к тому, что a истинно означает частичное доверие к тому, что a ложно и наоборот. Это приводит к ситуации, когда трудно отличить противоречивые суждения (различные источники утверждают о противоположном) от неопределённых (сведения «за» или «против» a неубедительны или их нет).

Помимо скалярного возможен интервальный подход [6, 7], но он тоже не всегда эффективен, поскольку если противоречивость ещё можно выразить некоторым подинтервалом, например, интервала [0,1], то отсутствие сведений вызывает проблему: непонятны размер и положение такого подинтервала, и как различить два типа интервалов? В этих условиях независимое накопление свидетельств «за» и «против» в векторе { a ⁺; а ^-) выглядит предпочтительным.

В теории нечётких множеств существует близкое к У^тр-семантике понятие интуиционистских нечётких множеств - IFS [8, 9], основанное на тройках { x, ^ A ( x), v A ( x )X где V A ( x ) — степень принадлежности элемента x множеству A (истинно, что x е A ); v A ( x ) - степень непринадлежности (ложно, что x е A ). Двойку {v A ( x ), v A ( x ) ) при этом можно рассматривать как аналог (1), но на v A ( x ) и v A ( x ) наложено ограничение:

0 A ( x)+ v A ( x ) < 1.                                      (2)

Это напоминает теорию свидетельств Г. Шафера [7] и отличает IFS и теорию свидетельств от V^TF. В V^TF-семантике и а ⁺ и а ^- могут совместно равняться 1, то есть:

0 < а ⁺+ а - < 2.                                         (3)

Различие принципиальное, поскольку (2) допускает, по существу, только состояние неопределённости (незнания, частичного знания), а (3) - и незнания, и противоречия(!).

1    Противоречия и неопределённость. Два вида противоречий

Вопрос о противоречии - один из фундаментальных в науке. Важен он и в задачах разработки систем, основанных на знаниях, системах поддержки принятия решений, иных подобных приложениях. Этот вопрос разделил логику Аристотеля и диалектику. В первой посту-лировалась(!) несовместимость утверждения и отрицания одного и того же в отношении одних и тех же вещей в одном и том же смысле и в один момент времени, во второй такое совмещение допускалось [10, 11] (нередко через нарушение принципов единства смысла и времени). Сложность состоит в том, что в практике часто предлагаются ситуации, когда приходится выбирать между двумя взаимоисключающими утверждениями. Запрет на их совместность представлен известной аксиомой:

—- (— । а &  а ), нарушение которой делает возможным вывод:

— а &  а ^ b , где b - любое суждение [12]. Если теория содержит противоречие, в ней выводимо что угодно, это обесценивает теорию и обосновывает запрет на противоречие.

Неприятие противоречий в теориях не избавляет от столкновения с ними на практике. Нередко при обработке эмпирического материала приходится иметь дело с взаимоисключающими данными. Ситуация взаимного исключения возникает, к примеру, при оценке осуществимости будущих случайных событий. Стремление учесть это обстоятельство породило теорию вероятностей и целый спектр многозначных логик (см., например [13, 14]).

Не менее значима и ситуация с дефицитом данных. Частный случай - дефицит доверия к ним, когда информация имеется, но полной уверенности в ней нет. Дефицит обрабатывается, например, теорией свидетельств или интуиционистскими нечёткими множествами, однако противоречивость в них, как и в нечётких логиках, допускается в ограниченном виде. В то же время и дефицит, и противоречивость формализуются семантикой V TF .

Когда говорят о формализации противоречия, рассуждают о противоречии вообще, не затрагивая причины и источники. В то же время надо выделить два его вида. Первый вид противоречия - информационный. В этом случае имеются исключающие друг друга сведения о состоянии объекта, хотя он в состоянии противоречия не пребывает. Например, из од- ного источника известно, что на улице солнечно, а из другого - что за окном снег или дождь (контрарность); или один сообщает, что идёт снег, а другой - что снега нет (контрадиктор-ность) и т.п. В любом случае состояние погоды (в данное время и в данном месте) какое-то одно, и истинно одно высказывание, однако при отсутствии иной информации приходится принимать решение, учитывая все источники. В Утг-семантике это делается присвоением разных значений компонентам вектора (1). Например, истинность утверждения a = «На улице идёт дождь» может выглядеть как || а ||=(0.3;0.1> или || а ||=(0.7;0.9> в зависимости от степени доверия к той и другой информации. Здесь первый (позитивный) компонент показывает основанное на свидетельствах доверие к тому, что дождь есть, а второй (негативный), что его нет. Доверие к обоим источникам может быть абсолютным, и тогда ситуация формализуется вектором (1;1> (полное противоречие свидетельств) или отсутствовать полностью - вектор (0;0> (неопределённость) [1].

Второй вид противоречия требует допущения, что противоречие существует реально, что оно свойственно природе объекта (имманентно ему). Иначе говоря, соответствующее утверждение истинно и ложно в одном и том же отношении в один и тот же момент времени в силу природы объекта(!). Это расходится с традиционными взглядами, но развитие вычислительных технологий подводит к такому представлению. Речь идёт о квантовых вычислительных устройствах. В основе квантовых вычислений лежит понятие кубита - квантового бита, который одновременно пребывает в состояниях 0 и 1, как если ложь и истина в них реализуются совместно (см., например [15, 16]). Если это принять за факт, тогда компоненты вектора (1) можно рассматривать как отражение совместности категорий Истины и Лжи в одном объекте (предмете, явлении, событии...). В таком случае а ⁺ и а - показывают, насколько утверждение совместно истинно и ложно согласно природе вещей. Соответствующие и отражающиеся в утверждении свойства не разделяются по времени и смыслу, а соединены в объекте. Этот вид противоречия можно назвать нативным . Квантовая механика не отделяет по времени и смыслу, например, пребывание электрона в состоянии со спином % от состояния со спином - %, или нахождение фотона в состояниях с разной поляризацией [15]. Эти состояния реализуются одновременно и неразрывны с объектом, присущи ему по своей природе. То есть явление можно трактовать как нативное противоречие. В квантовой механике это описывается суперпозицией волновых функций, а в У^тр-семантике - вектором (1). Именно для такого представления о противоречии предлагается ввести третью форму конъюнкции и дизъюнкции (хотя они могут трактоваться и информационно).

2    Третья форма конъюнкции и дизъюнкции. Свойства третьих форм

Первая форма конъюнкции и дизъюнкции определяется как [1]:

|| а & b ||= ( а *• b ⁺; а ^® b ^) ;                                        (4)

|| а v b ||= ( а ⁺® b ⁺; а - • b - > .                                          (5)

Здесь • и ® , соответственно, триангулированные (треугольные) норма ( t- норма) и ко-норма ( s- норма) в инфиксной записи, связанные дополнительно как: 1 - x • y =(1 - x ) ® (1 - у ); или, что аналогично: 1 - x ® у =(1 - x ) * (1 - у ); x , у е [0,1]. Примеры - пары функций x • у = min ( x , у ), x ® у = max ( x , у ); и x • у = x • у , x ® у = x + у - x • у . Вторая их форма определяется как [1]: || а &2 b ||= ( а + • b ⁺; а - • b - > ; || а V 2 b |^ ( а ⁺® b ⁺; а ~® b -) .

Первая форма - обобщение обычных (классических, а также нечётких) конъюнкции и дизъюнкции на семантику VTF. Это формализация естественно-языковых связок И и ИЛИ для векторного случая. Введение связей а++а ~=1 (аналогично, b++b ~=1) превращает (4) в нечёткую конъюнкцию, а (5) в нечёткую дизъюнкцию. Для вторых форм естественно-языковые связки предложить трудно - эта форма ни в классической, ни в нечёткой логике не встречается. Она носит информационный характер и выражает не конъюнкцию/дизъюнкцию явлений, а конъюнкцию/дизъюнкцию информации с учётом доверия к ней. Это информационные конъюнкция и дизъюнкция. Обе формы связок проиллюстрированы рисунком 1.

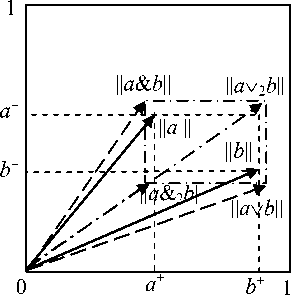
Рисунок 1 - Первая и вторая формы конъюнкции и дизъюнкции

Помимо этих двух пар связок, VTF- семантика включает две формы отрицаниями [1]. Первая форма отрицания:

|| — а ||= ( а ; а ⁺> ;

вторая форма:

||~ a ||= ( 1 - a ⁺;1 - а ~> .

Первая форма означает перестановку местами аргументов «за» и «против», вторая - отрицание в силу дефицита информации. Т.е. вторая форма отрицания, как и вторая форма конъюнкции и дизъюнкции, носит информационный характер.

В [17, 18] показано, что алгебра связок {1> (строгая ложь) и (1;0> (строгая истина) -аналогами 0 и 1 булевой алгебры - совпадает с алгеброй связок {1> и (1;0> заменить, соответствен- но, на (0;0> (неопределённость) и (1;1> (полное противоречие). Т.е. (0;0> и (1;1> здесь высту- пают в качестве нуля и единицы.

Третья форма конъюнкции и дизъюнкции обусловлена представлением о нативном противоречии как совместной реализации двух взаимоисключающих состояний. В качестве примера приведены кубиты, однако ситуацию можно представить и с более общих позиций. Отвлекаясь от физических особенностей, предлагается принять к сведению, что утверждение может быть истинным и ложным одновременно. Тогда конъюнкция а и b представляется как:

• || а &  n b ||= ( а *• b ⁺; а + • b “Ф а - • b ⁺® а - • b ^- > ,                              (7)

а дизъюнкция как:

• || а v n b ||= ( а *• b ⁺® а *• b ^-Ф а - • b ⁺; а - • b ^-> .                                (8)

Конъюнкция истинна в той мере, в какой а и b совместно истинны, и ложна в той, в какой ложно хотя бы одно из них. Аналогично, дизъюнкция истинна настолько, насколько истинно хотя бы одно утверждение и ложна настолько, насколько а и b совместно ложны. Для кубитов это описывается волновыми функциями, для векторов (1) используются триангулированные нормы. Третья форма конъюнкции и дизъюнкции называется нативной конъюнкцией и дизъюнкцией. Индекс « n » и прилагательное «нативный» здесь являются отсылкой к нативному противоречию.

В таблице 1 приведён сравнительный пример таблиц истинности для &, v , & 2 , v 2 и & n , v n при придельных значениях истинности Л(строгая ложь)= ( 0;1 > , И(строгая истина)= ( 1;0 > , Н(неопределённость)= ( 0;0 > , П(полное противоречие)= ( 1;1 > (первая и вторая формы таблиц взяты из [1]). Видно, что для значений вектора истинности, соответствующих классическим истине И= ( 1;0 > и лжи Л= ( 0;1 > , результаты для первой и третьей форм совпадают (выделено жирным). В отличие от первой формы, неопределённость ( 0;0 > для а или b порождает неопределённость для а &  _nb и а v _nb независимо от истинности второго элемента. Вторая форма конъюнкции и дизъюнкции - как обычные И и ИЛИ для значений истинности Н и П.

Для первой и второй форм конъюнкции и дизъюнкции справедливы соотношения де Моргана в следующем виде [1]:

( а &  b )— । а v—। b ; — । ( а v b ) = — а & — b ; ~( а & b ) = ~ а v ~ b ; ~( а vb ) = ~ а &~ b; ~( а & ₂ b ) = ~ а v ₂ ~ b ;

~( а v ₂ b ) = ~ а & ₂ ~ b . Но: — ( а & ₂ b ) = — а & ₂ — b ; — ( а v ₂ b ) = — а & ₂ — b .

Знак «=» здесь означает (логическую) эквивалентность - совпадение значений векторов истинности.

Таблица 1 - Таблицы истинности для различных форм конъюнкции и дизъюнкции

a	b	a & b	a v b	a &2 b	a v 2 b	a & n b	a v nb
Л	Л	Л	Л	Л	Л	Л	Л
Л	И	Л	И	Н	П	Л	И
Л	Н	Л	Н	Н	Л	Н	Н
Л	П	Л	П	Л	П	Л	П
И	Л	Л	И	Н	П	Л	И
И	И	И	И	И	И	И	И
И	Н	Н	И	Н	И	Н	Н
И	П	П	И	И	П	П	И
Н	Л	Л	Н	Н	Л	Н	Н
Н	И	Н	И	Н	И	Н	Н
Н	Н	Н	Н	Н	Н	Н	Н
Н	П	Л	И	Н	П	Н	Н
П	Л	Л	П	Л	П	Л	П
П	И	П	И	И	П	П	И
П	Н	Л	И	Н	П	Н	Н
П	П	П	П	П	П	П	П

Для третьей формы конъюнкции и дизъюнкции получается:

• — ( a & n b ) = — a v n — b ;                                (9)

• — ( a v n b ) = — a & n — b.                               (10)

Для проверки (9) достаточно сравнить векторы истинности левой и правой частей: || — ( a &  n b )|| = ( a ⁺* b ~® a - • b ⁺® a - • b ^- ; a ⁺* b ⁺) ; || — a v n — b || = ( a - • b ~® a - • b ⁺® a ⁺* b ^- ; a ⁺* b ⁺) .

Справедливость (10) подтверждается аналогично.

Для третьей формы конъюнкции и дизъюнкции, и второй формы отрицания соотношения подобные (9) и (10) отсутствуют. Это позволяет рекомендовать для работы с a &  n b и a v n b первую форму - отрицание в форме перестановки — .

Помимо (9) и (10) важно отметить следующие свойства, вытекающие из определения третьих форм и свойств триангулированных норм: a &  n b <  a v n b .

Также: a &  n b = b &  n a ; a v n b = b v n a ; || a &  n a || = ( a + • a ⁺; a + • a ~® a - • a ⁺® a - • a Э;

|| a v n a || = ( a + • a ⁺® a + • a ~® a - • a ⁺; a - • a ) .

Кроме того: a &  n Л = ( 0; a ⁺® a Э; a &  n И = a ; a &  n Н = Н; a &  n П = ( a ⁺; a ⁺® a ® a } <  a ;

И a v n Л = a ; a v n И = ( a ⁺® a ~;0 ) ; a v n Н = Н; a v n П = ( a ⁺® a ⁺® a ^- ; a } >  a .

Здесь < - отношение правдоподобия, означающее, что если a <  b ( a >  b ), то a ⁺<  b⁺ и a~ > b~ ( a ⁺ >  b ⁺ и a ^-< b ~) [1].

Видно, что свойство идемпотентности для a &  n b и a v n b , строго говоря, не выполняется. Не выполняется в общем случае и свойство ассоциативности. Его выполнимость требует дистрибутивности операций • и ® , что справедливо, например, для x • y = min ( x , y ) и x ® y = max ( x , y ), но несправедливо для x • y = x • y и x ® y = x + y - x • y .

Вектор И соответствует единице для & n , а Л - нулю для v n . Вектор Н оказывается своего рода «аннигилятором» для & n и v n : обе операции с ним дают в результате Н.

Изложенный принцип можно распространить на другие связки и отношения. В частности, помимо конъюнкции и дизъюнкции можно определить нативное исключающее ИЛИ (исключающую дизъюнкцию) как: || a XOR n b ||= ( a + • b ~® a ^-* b ⁺ ; a + • b ⁺® a ^-* b у нативную импликацию как: || a ^ n b ||=|| — a v n b ||= ( a + • b ⁺® a • b ⁺® a • b ; a + • b ) ;

нативную эквивалентность как: || a = n b ||= ( a + • b ⁺® a ^-* b ^- ;a + • b ® a ^-* b ⁺) ; и другие.

3 Обсуждение

Несмотря на то, что третьи формы конъюнкции и дизъюнкции введены с отсылкой к квантовой обработке информации, они не связаны напрямую с квантовой обработкой: V TF -семантика допускает понятие неопределённости вектора истинности 〈 0;0 〉 , чего нет в квантовой механике. Используемые в квантовых вычислениях волновые функции ψ 1 и ψ 0 состояний |1 〉 и |0 〉 подчиняются свойству | ψ 1 |²+| ψ 0 |²=1 [15, 16], что делает невозможной ситуацию неопределённости. При этом ψ 1 и ψ 2 описывают физический процесс , а не логику вообще. По этой же причине кубиты обрабатываются на основе единого физического закона, тогда как для векторов истинности может использоваться ряд t- и s- норм (см., например [19]). Отсылка к кубитам сделана для того, чтобы показать целесообразность понятия нативного противоречия, когда Истина и Ложь реализуются совместно.

Третьи формы введены для нативных противоречий и могут найти применение при принятии решений в условиях обработки информационных противоречий, дополняя первую и вторую формы. Особенность состоит в том, что неопределённость Н делает неопределёнными не только связки & n (И) и ∨ n (ИЛИ), но и новые введённые связки и отношения ∨ n , → n , = n , а также иные конструкции, «аннигилируя» их истинность (превращая её в Н).

Заключение

На основе представления о нативном противоречии для семантики V TF вводится понятие третьей формы конъюнкции и дизъюнкции (нативных конъюнкции и дизъюнкции) как дополнение к известным первой и второй формам, а также другие нативные связки и отношения. Из двух форм отрицания для работы с третьими формами конъюнкции и дизъюнкции рекомендуется использовать первую форму (вторая форма тоже может найти своё место). Третья форма совместно с нативными связками и отношениями может представлять интерес для информационного противоречия.