О трубчатых гиперповерхностях в евклидовом пространстве

Пусть 7 — простая регулярная кривая общего типа в евклидовом пространстве Е⁴, ~р = 7^(^ui) ^— векторное параметрическое уравнение кривой 7, отнесенное к натуральному параметру 77 6 [0,5]. Обозначим через "r^ui), nt(ui), ^(ui), n^tti) — векторы сопровождающего базиса Френе кривой 7 в точке "^(wi), где "т^ — "p'^i). Функции /ci(ui), ^(«i), k₃(ui) — первая, вторая и третья кривизны кривой 7 в точке "^(ui) соответственно. В нормальном пространстве кривой 7 в каждой точке "р (^м1) построим сферы 5²(t) с центрами в точках "р^х^) радиуса t, tky < о = const < 1, Со > 0. Множество сфер 5²(t) с центрами на кривой 7 в Е⁴ можно задать векторным уравнением

F^ : V = Т*^,^,^) = ~р (гц) + гЛ^гц, vi,u₂),             (1)

где A'(?zi, vi, v2) = cosui cosv2ni(ui) + cosVi sinv2n2(iii) + sin Vin3(ui).

Гиперповерхность F^ С E⁴ будем называть трубчатой гиперповерхностью вокруг кривой 7 на расстоянии t от 7*4^1) •

Пусть ж — произвольная точка F^, Т_ХЕ^ — касательное пространство к F^ в точке х. Пусть А^ : T_XF^ —> Т_ХЕ^ — оператор Вейнгартена относительно единичного нормального вектора £ в точке х. Обозначим через Ai, А₂, А₃ главные кривизны гиперповерхности F^ в точке х. Ai, А₂, А₃ являются собственными значениями оператора А^. Обозначим оу = Ai + А₂ + А₃, 02 = AiA₂ + AiA₃ + А₂А₃, <т₃ = АхА₂А₃ симметрические функции главных кривизн гиперповерхности F^ в точке х.

Теорема 1. Симметрические функции главных кривизн гиперповерхности F,³ С Е⁴, заданной уравнением (1), имеют вид:

.     . х        Ь COS th COS 022

o"i = Ai + Аг + Аз = ----—--,

1 — kTt COSVi cosv2 t x x \ \    \ \    1 Л 2/^cosuiCosu2 \

(72 — Л1Л2 + A1A3 + Л2Л3 — —  1 — ----— I , tz \    1 — kyt COS Ui COS 1)2 / k-v COS Ui cos v2

<73 = A1A2A3 = —----—-.

t^zVl — Kit COS У1 COSU₂)

Пусть Ry — оператор Риччи гиперповерхности F^ в точке ж. Обозначим через ri, 7₂, Тз собственные значения оператора Ну в точке ж.

Теорема 2. Собственные значения Ту, г₂, г₃ оператора Ry гиперповерхности

F^ С Е⁴, заданной уравнением (1), имеют вид:

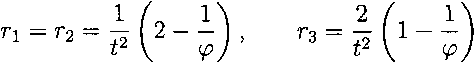
где р = 1 — k-^t cos Vi созиг-

Пусть Т^ — пространство дефектности гиперповерхности F^ в точке ж, ц_ж = dimT^⁰^ — индекс дефектности F^ в точке ж [1].

Теорема 3. Пусть гиперповерхность F^ С Е⁴ задана уравнением (1), где tky < 1/2. Тогда, если F^ имеет в точке х ненулевую третью симметрическую функцию главных кривизн <7₃ ^ 0, то F^ имеет в точке х нулевой индекс дефектности у_ж = 0.

• 1.    Доказательства теорем

Доказательство теоремы 1 опирается на следующую лемму.

Лемма 1. Главные кривизны гиперповерхности F^ С Е⁴, заданной уравнением (Г), имеют вид:

_{х Л} _   1 _Л ky cos vi cos v₂

Ai = An = —-, A3 = ----—---------.

t            V — kyt cos fi cos y₂

Доказательство. Обозначим через ||уу|| и ||Ьу|| матрицы первой и второй квадратичных форм F^, соответственно.

Найдем коэффициенты первой квадратичной формы F^. Мы имеем:

ди = (1 — fcitcosui cos V2)² + k^t² cos² vi + /c²<²(sin² ui + cos² Ui sin² v₂)— ^:

• — 2Ат2&з£²СО8и1СО8У2 8тУ1,   922 = t², 9зз = t² cos² Ui,  912 = &3£²sin²Ui,

913 = t² cos Ui ( k2 cos Vi — k₃ sin u_T cos u₂),     523 = 0.

Отсюда,

9П

^2’

У12

913 =

933 = -Т^—

Г2 COS V1

кз sin y₂ 22 _ 1 ^з sin^{2 y}i y)²   ’           r² +     y?²

кз cos Vi — кз sin Vi cos V2

COS

(fc₂ cos Vi — кз sin vi cos v₂)²

2₃ _ fc₂A;3sinv2

9        ^2

COS2 V1^2

kj sin vi sin y₂ cos v₂ cos Viy>²

где у? = 1 — fcitcos vi cosl’2. Единичный вектор нормали £ гиперповерхности F^

находим по формуле:

Мы получим:

£ = 2V(U1,V1,V₂) = COS V1 СО8У₂Й1(М1) + COS Vi sin V₂n₂('U₁) + sin Vin₃(ui).

Коэффициенты второй квадратичной формы гиперповерхности F^ имеют вид:

1 - k_xt COS Vi COS 1)2 - ди ,       922    ,       9^

Ou = ----------- "-----------,  Р22 = ,  O33 =—

,         912 ,         913 , n

012 — - —, 013 = - — > О2з = 0.

fv^-,         Тогда АТ = Ь^д^™,

Пусть ||А™|| — матрица оператора А^ в базисе где ||9jm|| = IlSijir1- Мы находим:

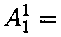
кх COS Vi COS 1)2

1 — tkx COS Vi COS 1)2

Д2 -— ДЗ — Д1 — дЗ — д1 — д2 — л

^2 _ (1 ^— ^1 COS Pi COSU₂)9¹²    «3   (1 — tkx COS Vi cosv₂)g¹³

Следовательно, собственные числа Ai, Л₂, A₃ оператора A^ являются корнями урав нения

/ ку cos vx cos d2       A / 1A

\1 — tfci COSU1 COSt>2    / \ t/

Таким образом,

.        1                kx COS 1)x COS 1)2

Ai = A2 = --, A3 = ----—-.

I          1 — kxt COS Vi COS 1)2

Лемма доказана.

Доказательство теоремы 1. Используя лемму 1, получим:

/С1 COS Vi COS V2 2

<7i — Ai 4- Л2 + А3 = ----—-,

1 — kit COS V1 COS V₂ t

t2 \    1 — kit cos Vi cos v2 / ki cos vi cos v2

СГ3 = A1A2A3 — —--—-.

t²^h — kitcosui cosv₂)

Теорема доказана.

Обозначим через R™ — элементы матрицы оператора Ri в базисе ^^, ^, ^) • Лемма 2. Элементы R™ матрицы оператора Ri имеют вид:

fli = fi= = ^ = ^ = 0, д; = Я= = -4_, где ip = 1 — k^t cos 01 cosu2-

• ' Доказательство. Компоненты R^km тензора Римана гиперповерхности F³ имеют вид:

О _ 512 । Л о _ 512513

^12,12 —     + V — 511)  -п-12,13 — —^—)  ^12,23 = 513)

о _ 91з , 9ззЛ. „ х „         912933 п         „

• ■    7113,13 "              ~ ^^П ’ ^/<13’^{23 —} —’ ^²³'^{23 — —}9зз-

• Следовательно, компоненты R^ = Rmtj формы Риччи гиперповерхности F3 имеют вид:

Ru — ^911 ^—     ^22 = кд₂2, R33 = ^9зз> ^12 = R21 = ^912,

R13 — R31 = /1913, R23 = R32 = О, где

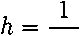
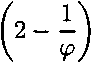
Отсюда, учитывая, что R¹^ = Rkjg^, приходим к утверждению леммы.

Доказательство теоремы 2. Собственные значения Г1,г₂,Гз оператора Ri являются корнями уравнения det(||^|| — гЕ) = 0. Учитывая лемму 2, получим следующее характеристическое уравнение:

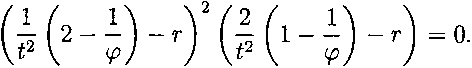
Отсюда получим утверждение теоремы.

Доказательство теоремы 3. Из неравенства tk^ <1/2 следует, что г_г ^ 0, г₂ + 0. Так как од =4 0 в точке ж, то г₃ ^ 0. Таким образом, р_$ = 0. Теорема доказана.

Из теорем 1, 2 вытекает следующее утверждение.

Теорема 4. Скалярная кривизна гиперповерхности Ff С Е⁴ совпадает с удвоенной второй симметрической функцией главных кривизн сг₂.

Доказательство. Так как скалярная кривизна R гиперповерхности F^ С Е⁴ равна сумме собственных значений оператора Ri, то из теорем 1, 2 получим:

Д = П + г₂ + г₃ = 2<т₂.

Теорема доказана.

Summary                        -

ON TUBULAR HYPERSURFACES IN EUCLIDEAN SPACE

Internal and external geometries of three-dimensional tubular surfaces in Euclidean space are studied in this article.