О вероятностном моделировании одного процесса взаимодействия частиц
Автор: Ассаул Виктор Николаевич, Головин Александр Викторович, Погодин Игорь Евгеньевич
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Математическое моделирование и обработка данных
Статья в выпуске: 3, 2019 года.
Бесплатный доступ
Анализируется и количественно моделируется динамический процесс случайного последовательного подлета частиц к системе ячеек, в которых при попадании двух частиц в ячейку происходит аннигиляция частиц с выделением некоторого количества энергии. Выбор ячейки для подлетающей частицы происходит случайным образом. В случае занятия пустой ячейки частица находится в этой ячейке до подлета следующей частицы. Рассматриваются различные соотношения числа частиц и ячеек, проанализированы предельные случаи. Модель предложена для процессов хемилюминесценции, в ходе которых происходит выделение световой энергии вследствие химической реакции. Используются методы классической теории вероятностей с построением деревьев исследуемых событий. Представленная модель носит упрощенный ха -рактер, но допускает дальнейшее обобщение на случай более точного учета протекающих процессов. Кроме того, задача имеет выход на модель простейших потоков с приложениями в теории систем массового обслуживания.
Занятые и свободные ячейки, подлетающая частица, порядковый номер, вероятность высвечивания, дерево структуры состояний
Короткий адрес: https://sciup.org/148308944
IDR: 148308944 | УДК: 51-7 | DOI: 10.18101/2304-5728-2019-3-60-68
On probability simulation of one particle interaction process
The article analyzes and quantitatively simulates the dynamic process of a random subsequent approach of particles to a system of cells. When two particles enter the cell, the particles annihilate with the release of a certain amount of energy. The selection of cell for the approaching particle is random. If an empty cell is occupied, the particle is in this cell until the next particle approach. We have considered various correlations of the number of particles and cells, analyzed the limiting cases. It is proposed a model for chemiluminescense processes, during which light energy is released due to a chemical reaction. We have used the methods of classical probability theory with the construction of trees of the events under investigation. The presented model is simplified, but allows further generalization for more accurate accounting of ongoing processes. In addition, the problem has a link to a model of simple flows with applications in counter theory.
Текст научной статьи О вероятностном моделировании одного процесса взаимодействия частиц
В данной работе на основе вероятностных представлений проведена попытка смоделировать динамический процесс последовательного подлета возбужденных частиц к поверхности с определенным набором ячеек, в которых происходит как накапливание энергии (на первой стадии), так и высвечивание всей энергии на второй стадии. Рассматривается задача, в которой предполагается, что n частиц случайным образом последовательно прилетают в к ячеек. В случае попадания двух частиц в одну ячейку идет моментальное высвечивание некоторого количества энергии, частицы аннигилируют, а ячейка готова снова принимать новые частицы на прежних условиях высвечивания. Требуется исследовать временную динамику вероятности (интенсивности) высвечивания в зависимости от размера системы к и от номера n очередной прилетевшей частицы.
Такая ситуация проистекает из физических исследований по хемилюминесценции [1]. Хемилюминесценция — это эмиссия света (люминесценция) в результате химической реакции. При этом энергия химической реакции переходит в энергию света и несет информацию о произошедшей химической реакции. В случае поверхностной хемилюминесценции при атмосферных условиях активная частица подлетает к поверхности и передает ей свою энергию, которая после определенного преобразования на активных центрах поверхности высвечивается в виде фотона. В одной из известных реакций взаимодействия возбужденного синглетного кислорода 1 с поверхностью кристаллического 9,10-дифенилантрацена энергия кванта люминесценции дифенилантрацена более чем в два раза превосходит энергию возбуждения молекулы синглетного кислорода [3]. Учитывая закон сохранения энергии и статистическое распределение тепловой энергии на поверхности кристалла, разумно предположить, что энергия от синглетного кислорода первоначально сохраняется и накапливается в активных зонах (ячейках), а процесс высвечивания происходит только после попадания последующей молекулы синглетного кислорода в активную зону (ячейку).
Кроме того, моделируемая задача близка к модификации распространенной модели «простейшего процесса» 2 [4], в котором свойство «ординарности», т. е. запрет на одновременное попадание двух «частиц-заявок», заменено на аннигиляционное высвечивание с уничтожением частиц; в приложении теории очередей, например, к движению автотранспорта, это может быть столкновение пары случайно сблизившихся транспортных единиц (ДТП) с их дальнейшим уходом из процесса.
Наконец, задача может служить полезным методическим упражнением для изучающих теорию вероятностей (раздел «Случайные события») в объеме, соответствующем программе технического вуза [5].
Построение и исследование модели
Для начала рассмотрим и смоделируем поведение системы при увеличении количества частиц n с незначительным количеством ячеек k в переходной фазе из начального состояния покоя ( n 0 = 0 ) и оценим вероятности высвечивания P ( к ) (здесь P (...) означает условную (или безусловную) вероятность высвечивания после подлета частицы с указанным в скобках номером при соответствующих условиях относительно предшествующих частиц). К примеру, P (4|2,3) означает вероятность высвечивания при подлете 4-й частицы при условии, что предыдущее высвечивание было при подлете 3-й частицы и отсутствовало при подлете 2-й частицы.
Начнем с более подробных вычислений при к = 3 . Тогда:
у первой (n = 1) прилетевшей частицы P(1) = 0, у второй (n = 2): P (2) = 1/3, у третьей (n = 3): P (3|2) = 0, P (3|) = (1 - P (2)) ■ 2/3 = 4/9;
у четвертой ( n = 4 ):
P (4|2,3) = (1 - P (1))(1 - P (2))(1 - P (3|2)) = 2/9;
P (4|2,3) = (1 - P (1)) P (2)(1 - P (3|2)) ■ 1/3 = 1/9;
P (4^,3) = (1 - P (1))(1 - P (2)) P (3|2) = 4/27;
и в итоге P (4) = 13 / 27 .
У пятой ( n = 5 ):
P (5) = P (5| 2,3,4) + P (5| 2,3,4) + P (512,3,4) =
= (2/9 + 8/27 + 2/9) ■ 2/3 = 40/81.
Аналогично при к = 2 : P (1) = 0 , P ( n > 2) = 1/ 2 .
При к = 4 :
P (1) = 0 , P (2) = 1/4 , P (3) = 3/8 ; P (4) = 7/16 ; P (5) = 15/32 ; P (6) = 31/64.
При к = 5 : P (1) = 0 ; P (2) = 1/5 ; P (3) = 8/25 ; P (4) = 49/125 ; P (5) = 272/625 .
Для построения дерева найдем сначала рекуррентное соотношение для вычисления вероятности высвечивания P ( n + 1) при прилете очередной частицы (шаг увеличения n на единицу):
P ( n + 1)
k
Е j=1
к - s j k
к — s ■ — 1 s: к — s ■ +1 ----j ---+ —L--j--- k kk
P j ( n ) ,
где s j — количество пустых ячеек в каждом j -м компоненте, имевшем веро ятность p j (n), среди компонент, относившихся к предыдущему шагу n .
На основании проделанных эмпирических пробных расчетов можно построить обобщенное выражение
P ( k , n ) = 0.5
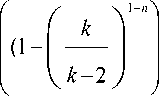
к > 2 ,
lim P ( n )| к « 0.5. n ^го
Рассмотрим состояние (s, к — s) с s занятыми и (к — s) свободными ячейками, вероятность высвечивания из которого составляет: s / к. После прилета (n +1) -й частицы система может с вероятностью s / к перейти в состояние (s — 1, к — s +1) , откуда при прилете следующей (n + 2) -й частицы возможно высвечивание с вероятностью (s — 1) / к, либо с вероятностью (1 — s / к) переход в состояние (s +1, к — s — 1) , откуда при прилете (n + 2) -й частицы возможно высвечивание с вероятностью (s +1) / к. В итоге после прилета (n + 2) -й частицы система может дать высвечивание с вероятностью:
( s / к )( s — 1)/ к + (1 — s / к )( s + 1)/ к = ( s / к ) [ 1 — 2/ к + 1 /( sk ) ] . (2)
При возможности пренебрежения в (2) членом 1/( sk ) , например, если s >> 1 , можно получить P ( к , n + 1) — P ( к , n ) [ 1 — 2/ к ] , т. е. вероятность высвечивания менялась бы строго по закону геометрической прогрессии. Однако если считать величину s случайной, равномерно распределенной в диапазоне [ 0 ^ к ] , то усреднение вероятности (2) по этому диапазону s дает выражение: (0.5 — к 1 + к 2 ) , также сходящееся к 0,5 при увеличении к .
Далее с помощью построения «деревьев» рассмотрим по шагам начало релаксации системы при различных видах начальных условий, а именно:
-
А) после момента полного заполнения к частицами всех к имеющихся ячеек;
Б) после момента гипотетического заполнения к частицами половины всех ячеек, т.е. ровно q из имеющихся к = 2 q ячеек;
-
В) после момента полной пустоты всех к имеющихся ячеек.
Во всех случаях процесс расчета вероятностей представим в виде таблицы, изображающей соответствующее дерево динамики событий с указанием номеров последовательных шагов n (подлет очередной частицы с номером n ) после момента полного заполнения ячеек (случай (А), табл. 1) и вероятностей высвечивания в соответствующих состояниях (случаи (А), (Б) и (В), табл. 2).
Таблица 1
|
г W 02 Н О о о S в У В н о Г н о в В в В в W S cd 02 S о 02 О 02 о о о Он о m |
Дерево динамики состояний системы из к ячеек, изначально полностью занятых частицами (случай (А)) |
|||||||||||||
|
к = 0 |
||||||||||||||
|
1 |
1 |
|||||||||||||
|
( к - 1) + 1 |
||||||||||||||
|
2 |
( к - 1)/ к |
1/ к |
||||||||||||
|
( к - 2) + 2 |
к + 0 |
|||||||||||||
|
3 |
( к - 2)/ к |
2/ к |
1 |
|||||||||||
|
( к - 3) + 3 |
( к - 1) + 1 |
( к - 1) + 1 |
||||||||||||
|
4 |
( к - 3)/ к |
3/ к |
к - 1 k |
1 |
к - 1 k |
1 k |
||||||||
|
( к - 4) + 4 |
( к - 2) + 2 |
( к - 2) + 2 |
к + 0 |
( к - 2) + 2 |
||||||||||
|
к + 0 |
||||||||||||||
|
5 |
к - 4 k |
4 k |
к - 2 k |
2 k |
к - 2 k |
2 k |
1 |
к - 2 k |
2 k |
1 |
||||
|
( к - 5) + 5 |
( к - 3) + 3 |
( к - 3) + 3 |
( к - 3) + 3 |
|||||||||||
|
( к - 1) + 1 |
( к - 1) + 1 |
( к - 1) + 1 |
||||||||||||
Таблица2
|
№ n |
Вероятность высвечивания после прилета n -й частицы при условии, что в исходном состоянии: |
||
|
все ячейки заняты (А) |
занята половина всех ячеек (Б) 1/2 |
все ячейки свободны (В) |
|
|
1 |
1 |
0 |
|
|
2 |
1 - 1/ к |
1/ к |
|
|
3 |
1 - 2/ к + 2/ кг |
2/ к - 2/ кг |
|
|
4 |
1 - 3/ к + 6/ к 2 - 4/ к3 |
3/ к - 6/ к 2 + 4/ к3 |
|
|
5 |
, 4 12 16 8 1 ++ к к 2 к3 к4 |
4 - 12 16 - 8 к к7 + к7 к 4 |
|
|
6 |
, 5 20 40 1 -- + - + к к2 к3 40 16 + к4 к5 |
5 20 40 ---т +----- к к2 к3 40 16 к4 + к5 |
|
|
n |
1 - Е l ( - 2) , - 1 СП - 1/ к1 |
VJ 2) Cin - 1/ к |
|
Можно заметить, что для случая (А) (со временем после момента гипотетического полного занятия всех ячеек) вероятность высвечивания падает сверху, стремясь к некоторому пределу, для случая (В) вероятность высвечивания растет снизу, стремясь к пределу. Примечательно, что случаи (А) и (В) обнаруживают симметрию относительно значения вероятности 0.5.
В случае (Б) вероятность высвечивания устанавливается на уровне 0.5 независимо от количества прилетевших частиц.
Тот же случай (А) при к = 3 можно рассмотреть также, используя комбинаторику в модели различимых частиц (табл. 3), что несущественно:
Таблица 3
|
IS о H 2 св Н о В У О 8 Д во а о S о £ К г |
02 Он cd £ а |
в У )В В S св и В со н в £ О о Ы в |
в 8 Он г 8 ° cd о 5 о СО в о л и 5 у в <5 се £ |
в в « со В О у 02 cd н О ° g в к а н а К Щ н Ооо а СО I-H ООО m в в |
В о в к со а в в СО в н & § о a s Н 8 О § § 8 & § D§ Щ 02 02 |
в S о В о о 5 В В 8 w В 38 о S ° во а о о 5 2 со « 8 «So 5 8 н Soo а со в Bos ° а С со В |
|
|
3 |
2:0:0 |
3 |
C 2 2 = 1 |
1/3 |
0 |
||
|
1:1:0 |
3 |
C 12 = 2 |
2/3 |
2/3 |
|||
|
6 |
9 |
4/9 = 0.44 |
|||||
|
4 |
3:0:0 |
3 |
С 33 = 1 |
1/9 |
1/3 |
||
|
2:1:0 |
6 |
С 23 = 3 |
2/3 |
1/3 |
|||
|
1:1:1 |
1 |
P 3 = 6 |
2/9 |
1 |
|||
|
10 |
27 |
13/27=0.48 |
|||||
|
5 |
4:0:0 |
3 |
C 44 = 1 |
1/27 |
0 |
||
|
3:1:0 |
6 |
C 34 = 4 |
8/27 |
2/3 |
|||
|
2:1:1 |
3 |
С 2 4 P 2 = 12 |
4/9 |
2/3 |
|||
|
2:2:0 |
3 |
С 24 = 6 |
2/9 |
0 |
|||
|
15 |
81 |
40/81 = 0.49 |
|||||
|
6 |
5:0:0 |
3 |
C 55 = 1 |
1/81 |
1/3 |
||
|
4:1:0 |
6 |
C 45 = 5 |
10/81 |
1/3 |
|||
|
3:1:1 |
3 |
C 3 5 P 2 = 20 |
20/81 |
1 |
|||
|
3:2:0 |
6 |
C 3 5 = 10 |
20/81 |
1/3 |
|||
|
2:1:2 |
3 |
C 23 C 52 = 30 |
10/27 |
1/3 |
|||
|
21 |
213 |
121/243 = = 0.498 |
|||||
Заключение
В работе построено дерево переходов при подлете новых частиц при различных начальных условиях и рассчитана динамика вероятностей высвечивания. Получены вероятности высвечивания при малых k комбинаторным образом для классического определения вероятности. Получено аналитическое выражение для вероятности высвечивания, найдены аналитические выражения для коэффициентов для найденных вероятностей, кроме того, дана интерпретация полученных оценок вероятностей.
Список литературы О вероятностном моделировании одного процесса взаимодействия частиц
- Колтовой Н. А. Хемилюминесценция. М.: Nethouse.ru, 2017. 145 с.
- Schwetzer C., Schmidt R. Physical mechamisms of generation and deactivation of singlet oxygen // Chemical Revue, 2003. V. 103 (5). P. 1685-1758.
- Челибанов В. П., Челибанова М. Г. Способ и устройство для регистрации синглетного кислорода // Патент RU 2415401 C1, 2010.
- Вентцель Е. С. Исследование операций: задачи, принципы, методология М.: Наука, 1988. 203 с.
- Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа, 2014. 480 c.
