О визуализации анизотропии дисперсии скоростей полидисперсной пыли в газопылевой среде

DOI:

Ровно так же, как в газовой динамике газодинамические разрывы (ударные фронты, тангенциальные или контактные разрывы) являются ключевыми деталями для восстановления газодинамического портрета в целом, в динамике бесстолкновительных сред такими деталями служат области динамических особенностей течения — точки поворота, точки стагнации, точки накопления, области многопотоковости, бесстолкновительные ударные волны [2; 4]. Там, где траектории частиц пересекаются, образуются в свою очередь структурные особенности бесстолкновительной среды — складки, «пелены», каустики.

В случае бесстолкновительных сред специального вида, а именно примесей малых твердых частиц, погруженных в несущую газовую фазу (запыленные газы), предполагается наличие сильного трения между твердыми частицами и газом, а флуктуационными скоростями включений и, соответственно, собственными напряжениями обычно прене-брегается.

Если же учесть конечную инерцию включений и конечность флуктуационных скоростей, то следует отметить, что одной из отличительных динамических особенностей дисперсной фазы является возможность дисперсии скоростей частиц быть анизотропной. В отличие от этого в газовой динамике дисперсия скоростей сплошной среды характеризуется не тензором, а одним числом — температурой, что подразумевает сохранение изотропии в распределении частиц газа по скоростям в любой точке среды в любой момент времени.

Распространенной является точка зрения, согласно которой движение примесной фазы можно моделировать, либо предполагая примесь полностью «вмороженной» в несущую фазу, либо рассматривая примесные частицы как малоинерционные, так что их отклонение от линий тока несущей фазы незначительно. Часто в таких случаях используется уравнение Крамерса — Фоккера — Планка [12], которое подразумевает преобладание силы трения над всеми остальными силами, действующими на частицы.

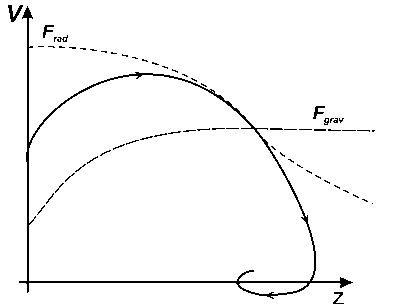
Рис. 1. Фазовая кривая на плоскости «вертикальная координата — вертикальная скорость», иллюстрирующая движение пыли под действием сил давления излучения и гравитации в газопылевом облаке [1]. Газ при этом рассматривается как находящийся в гидростатическом равновесии. В точке баланса сил происходит накопление пыли. Течение пыли в окрестности точки накопления приобретает многопотоковый характер

В условиях, когда на примесные частицы действуют сторонние объемные или поверхностные силы, как, например, в задаче о динамическом равновесии самогравитиру-ющего оптически толстого газопылевого межзвездного облака (см. рис. 1 и подпись к нему), эти сторонние силы могут существенно превышать силу трения.

Однако, даже если в среде отсутствуют какие-либо иные силы, действующие на примесную частицу, кроме силы трения, в случае достаточно инерционных частиц выполнение условий приближения Крамерса — Фоккера — Планка отнюдь не гарантировано.

Рассогласование движений дисперсной и несущей фаз происходит в ударных волнах с частичной дисперсией , в которых на фронте волны параметры течения несущей фазы претерпевают разрыв, а параметры дисперсной фазы непрерывны. В областях за фронтами таких ударных волн происходит релаксация параметров течения дисперсной фазы. И наоборот, результатом прохождения последовательности ударных фронтов может стать многопотоковое течение примесной среды с пересечением траекторий. Возможно также специфическое рассогласование движений примесной и несущей фаз такое, которое приводит к появлению сглаженных ударных переходов, в которых гидродинамический разрыв в несущей фазе отсутствует — так называемым волнам с полной дисперсией [13]. Наконец, могут существовать течения без всякого сингулярного поведения концентрации, но такие, в которых значительные относительные движения потоков не просто существуют, но играют важную роль в динамике среды. Например, в случае, если относительное движение потоков в бесстолкновительной плазме происходит со скоростью, превышающей тепловую, в среде развивается двухпучковая неустойчивость [2].

В последние годы возник большой интерес к изучению и, соответственно, численному моделированию динамики полидисперсных смесей [6; 11]. Поведение отдельных фракций пылевых частиц позволяет провести диагностику состояния несущей фазы. Например, в астрофизике ударные волны в разреженном межзвездном газе зачастую невозможно наблюдать непосредственно, так как газ почти не вызывает экстинкцию света, в то время как экстинкция на пыли велика.

Удобным качественным инструментом анализа течений газопылевой среды служит визуализация областей локализации структурных особенностей течения — каустик, складок и т. д. Развиваются специальные приемы описания поведения дисперсной примеси в течениях с разрывами сплошности, множественными пересечениями траекторий частиц и локальными зонами накопления дисперсной фазы с помощью дополнительных уравнений, выделяющих особенности [3]. Однако для описания течений, в которых областей многопотоковости много (в пределе вся расчетная область представляет собой многопотоковое течение), прямое численное моделирование динамики примесной фазы методом частиц обладает существенными преимуществами — простотой и экономичностью описания и, соответственно, компьютерного моделирования.

Авторами в работе [14] предложен оригинальный алгоритм, основанный на использовании энтропийной меры, позволяющий визуализировать пространственные распределения концентраций до трех фракций пылевых частиц одновременно при численном моделировании динамики пылевой компоненты гетерогенной газопылевой среды методом частиц.

Однако, как следует из описанного выше, структурные особенности не обязательно пространственно совмещены с динамическими особенностями. Для визуализации динамических особенностей требуются специальные методики. В настоящей статье мы рассматриваем способы визуализации пространственного распределения анизотропии дисперсии скоростей полидисперсной пылевой компоненты газопылевой среды как отдельно для каждой пылевой фракции, так и сразу для всех пылевых фракций одновременно. В последнем случае мы предлагаем использовать энтропийную меру полидисперсности.

1.    Численная модель газопылевой среды

Мы развиваем инструменты визуализации на примере двумерной динамической модели турбулентного газопылевого облака. Детали моделирования, основные уравнения, обоснования применимости тех или иных приближений можно найти в нашей работе [14]. Здесь мы только кратко перечислим основные черты модели.

• I)    Рассматривается течение в расчетной области, имеющей форму квадрата. Количество расчетных ячеек равно Ы_ж х N_y, где Ы_ж = N_y = 1 024.

• II)    Несущая фаза считается столкновительным одноатомным совершенным газом. Течение газа описывается как адиабатическое. В расчетах показатель адиабаты газа брался равным 5/3.

• III)    Дисперсная фаза рассматривается как скалярная примесь. Динамика отдельных примесных частиц — пылинок — рассчитывается путем прямого численного моделирования методом частиц.

• IV)    Учитывается влияние силы трения пылинок о газ, обратное влияние пыли на газ не учитывается.

• V)    Пылевая компонента рассматривается как полидисперсная смесь трех различных фракций. Соответствующие числа Стокса (напомним, число Стокса характеризует относительное время динамической релаксации частиц за счет вязкого трения) равны для крупных частиц Sk = 1, для частиц средних размеров Sk = 0,1 и для мелких частиц Sk = 0, 01.

• VI)    Количество частиц для каждой фракции задается равным 3,5 • 106, что соответствует долевому участию в 3,3 частицы каждой фракции в каждой расчетной ячейке в среднем.

• VII)    Количество пылинок в расчетной области остается неизменным в течение всего процесса моделирования. И для газа, и для пыли задаются периодические граничные условия.

• VIII)    Турбулентность генерируется с помощью случайных сил. В реализации процедуры генерации турбулентности следуем работам [5; 7; 10].

2.    Визуализация распределения анизотропии дисперсии скоростей монодисперсной пыли

Распределения каждой фракции, а также газа для некоторого момента времени в расчетах, когда турбулентность вышла на околозвуковой режим и установилась, демонстрирует рисунок 2. Пылинки фракции крупных частиц сильнее кластеризованы, чем представители других фракций, и четко очерчивают периферии турбулентных вихревых ячеек.

Все описываемые в настоящем разделе величины вычисляются индивидуально для каждой фракции.

Находим массовую скорость V пылевой компоненты в ячейке расчетной области с координатами (i,j ) , суммируя по скоростям всех частиц, находящихся в данной ячейке:

V(i, j ) =    ^   v«(x« ,Уа),     i = 1,Nx,j = 1,Ny.

а

( X a ,ya' ) E ( i,j' )

Далее определяем флуктуационные скорости иа частиц и«(ха,Уа) = va(xa,ya) - V(i,j),     (ха,у») Е (i, j),     i = 1, Nx, j = 1,N.

Тензор дисперсии скоростей определяется как симметричный

D(i, j) = uaua , следовательно, он имеет два вещественных положительно определенных собственных значения d1(i, j) и d2(i,j).

Пусть для определенности d 1 >  d ₂ . Величины d 1 и d ₂ по смыслу являются квадратами полуосей эллипса дисперсии скоростей, а направления, задаваемые собственными векторами тензора D , — главными. То направление, которое соответствует большему собственному значению d 1 , назовем главным направлением.

Эксцентристет эллипса

e(u) = TlT^iEj l                     (4)

^e(i,j) V¹ d i (i,j)                                       ⁽⁴⁾

принимает значения в интервале [0,1] . Изотропному распределению дисперсии скоростей отвечает значение е = 0 , полностью анизотропному — е = 1 .

Распределения эксцентристетов эллипса дисперсий скоростей для каждой из фракций для того же момента времени, что и на рисунке 2, показаны на рисунке 3.

При наличии цветной печати изображение может быть в принципе более информативным, с учетом того, что цвет есть информационно-емкий ресурс [8; 14]. В случае монохромного изображения дополнительную информацию о распределении могут нести некоторые символы-маркеры, так называемые глифы. Простейшими глифами служат стрелки, позволяющие визуализировать векторное поле. В случае тензорных полей в качестве глифов применяют различные фигуры, меняющие свою форму в зависимости от сочетания инвариантов тензора [9; 15].

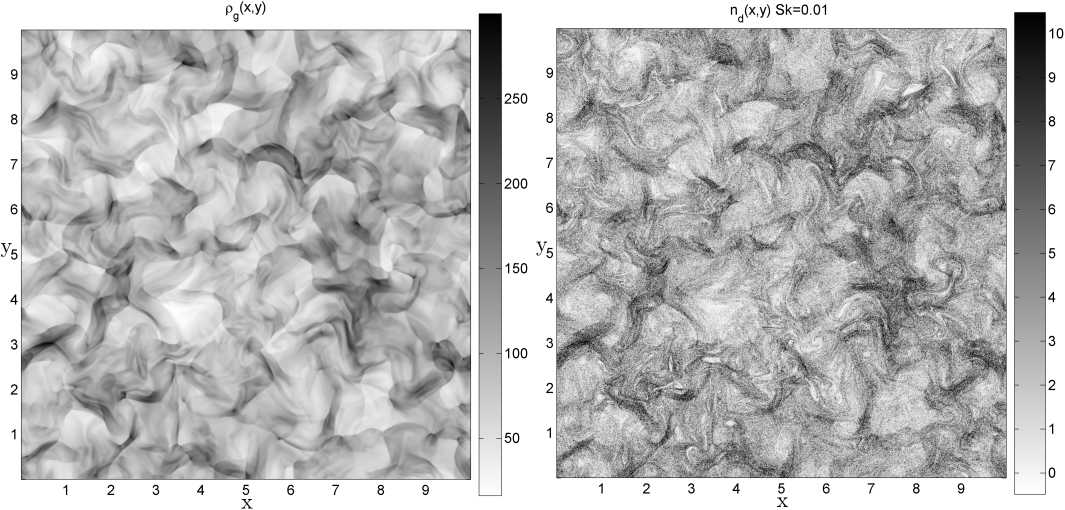
Рис. 2. Состояния несущей газовой фазы и полидисперсной пылевой компоненты в численном двумерном гидродинамическом моделировании течения турбулентной газопылевой среды в некоторый характерный момент времени после установления развитой околозвуковой турбулентности.

Сверху слева — распределение концентрации газа, на остальных рисунках — распределения концентраций примесных пылевых частиц, в том числе сверху справа — для пылинок с числом Стокса, равным 0,01 (мелкие частицы), внизу слева — для пылинок с числом Стокса, равным 0,1 (частицы средних размеров), внизу справа — для пылинок с числом Стокса, равным 1 (крупные частицы). Шкала величин линейная, используются некоторые условные относительные единицы длин и концентраций

В качестве глифов мы для большей наглядности на верхнем правом рисунке 2 тонкими черными отрезками отмечаем направления главной оси эллипсов дисперсии скоростей. Ячейке расчетной сетки, в которой определяется направление главной оси, сопоставляется центр отрезка. Длины отрезков пропорциональны величине соответствующего главного значения тензора дисперсии скоростей. Опыт показал, что визуализация главных осей в случае изображений с большой детализацией разномасштабных структур не всегда удобна. Если кластерам пыли отвечают более тонкие и более контрастные прожилки, как это имеет место в случае фракций средней и крупной пыли, отрезки сливаются с прожилками и плохо читаемы.

3.    Визуализация распределения анизотропии дисперсии скоростей полидисперсной пыли

Для визуализации распределений анизотропий дисперсий скоростей сразу для нескольких фракций одновременно на одном рисунке нами предлагается в духе нашей работы [14] представлять эти распределения с помощью некоторого показателя (функции признаков объектов), характеризующего степень разнообразия распределения признаков в выборке. В качестве меры разнообразия часто принимают энтропию Шеннона.

В настоящей работе мы предлагаем некоторую модификацию энтропии Шеннона, которую мы называем суррогатной энтропией.

Рассмотрим алгоритм вычисления энтропии для случая смеси двух фракций. Определим суррогатную энтропию по следующему правилу:

' - ^{£ £} p ' l°g 4 (p ‘ ^a) ), a =1 i =1

2 + £ pV ^lOg 4 ⁽p ^{() )}, г =1

0,

обе фракции представлены в ячейке;

только одна фракция представлена в ячейке; ни одной фракции не представлено в ячейке.

Здесь индекс а отмечает соответствующую фракцию, индекс г — порядковый номер главной оси.

Величины p 1 ^a) в (5) определяются как относительные длины полуосей эллипса дисперсии для каждой фракции в отдельности в соответствии с формулой

р p? = < n$ №+<№'

0,

если фракция в ячейке представлена;

если фракция в ячейке не представлена.

Здесь N j — количество фракций, представленных своими частицами в ячейке. Например, если частицы обеих фракций присутствуют в ячейке, то N j = 2 , если только одной, то N j = 1 . В случае, если ячейка свободна от пыли, то деление на N j не производится, все четыре величины р _г- ^а) полагаются равными нулю в соответствии с определением (6).

При таком подходе случай, когда оба эксцентриситета для обеих фракций близки к нулю, почти не будет различать ситуации, когда эксцентриситеты слегка отличны от нуля. Эти случаи отвечают равновзвешенной смеси с максимальной энтропией, равной — log ₄ (1/4) = 1 , что отображается черным цветом.

Средний по тону серый цвет отмечает комбинацию, при которой дисперсии скоростей обеих фракций полностью анизотропны. Тогда суррогатная энтропия равна

— log 4 (1/2) = 0,5.

Рис. 3. Распределения особенностей дисперсий скоростей полидисперсной пыли для того же момента времени, что и на рисунке 2. Вверху слева — распределение энтропии для фракций пылинок малых и средних размеров (правила вычисления энтропии см. в п. 3), на остальных рисунках — распределения эксцентриситетов эллипсов дисперсий скоростей, в том числе вверху справа — для пылинок с числом Стокса, равным 0,01 (мелкие частицы), внизу слева — для пылинок с числом Стокса, равным 0,1 (частицы средних размеров), внизу справа — для пылинок с числом Стокса, равным 1 (крупные частицы)

Такой же по тону серый цвет отмечает случай, когда одна из фракций отсутствует, а дисперсия скоростей второй фракции полностью анизотропна. Энтропия опять равна 0,5 + log 4 (1) =0,5 .

В случае когда в ячейке присутствует только одна фракция и ее дисперсия скоростей полностью изотропна, энтропия принимает минимально возможное в рамках данной задачи значение, равное 0, 5 + log ₄ (1/2) = 0 . Этому значению энтропии сопоставляется белый цвет.

Тот же белый цвет сопоставляется пустым ячейкам, свободным от пыли.

Распределение суррогатной энтропии представлено на верхнем правом рисунке 3.

Выводы

• 1.    В настоящей работе предложен инструмент визуального анализа многомерных данных — построение карт пространственного распределения динамических особенностей многофазной сплошной среды. Под многофазной понимается газовая среда, содержащая примесные твердые (пылевые) частицы, причем примесь характеризуется распределением частиц по размерам (полидисперсная смесь), что соответственно влечет распределение частиц по их динамическим характеристикам, таким как подвижность.

• 2.    Особенность предлагаемого подхода состоит в возможности визуализации степеней анизотропии одновременно для нескольких фракций частиц. Это реализуется с помощью специальным образом сформированной энтропийной функции, которую мы здесь называем суррогатной энтропией. Приведены распределения энтропии для случая смеси из двух фракций. Возможности визуализации могут быть расширены при использовании цветовой палитры. Цвет как информационно-емкий ресурс позволит визуализировать одновременно большее число фракций.

• 3.    Демонстрационные расчеты показывают, что пространственные перепады степени анизотропии в распределении дисперсии скоростей примесной пылевой компоненты, начиная с масштабов самых крупных турбулентных вихрей и мельче, — гигантские и имеют максимально возможный размах. Анизотропия, выражаемая количественно в мерах эксцентристета эллипса дисперсии скоростей, меняется от минимально возможного значения 0 до максимально возможного значения 1.

• 4.    Области максимальной анизотропии дисперсии скоростей пространственно совмещены с плотными волокнами кластеризованной пыли, которые преимущественно протягиваются вдоль границы вихрей. Данный феномен объясним — на границах вихрей пылинки испытывают эффекты центрифугирования, либо претерпевают резкие перепады силы трения на ударных скачках, которые преимущественно сосредоточены на периферии вихрей. В то же время в центре вихрей одновременно с понижением концентрации пыли дисперсия скоростей оказывается гораздо более изотропной.

В качестве визуализируемых данных рассматривается пространственное распределение областей анизотропии дисперсии скоростей пылевых частиц. Зонам сильной анизотропии дисперсии скоростей отвечают области, в которых возникает интенсивное многопотоковое течение. Характерным примером могут служить бесстолкновительные ударные волны, точки поворота течения, точки стагнации.