О влиянии напряженного состояния артерии на скорость распространения пульсовой волны

Представим артерию в виде бесконечно длинной ортотропной упругой цилиндрической оболочки радиуса R и толщины h , работающей в условиях моментного напряженного состояния. Жидкость (кровь) предполагается ньютоновской и несжимаемой, а ее движение – ламинарным и осесимметричным. Окружающую тканевую среду будем представлять как упругое бесконечное пространство с цилиндрической полостью, где помещена артерия. Среда препятствует движению артерии только в радиальном направлении [5].

Согласно принятым предположениям вопрос распространения пульсовой волны сводится к исследованию следующих уравнений [5-8].

Уравнения движения артерии

∂ ² u      ∂ w    ∂ ² u 4 νρ ₁

B ₁₁     + B =ρ - V ,

• ¹¹    ∂ x ^{2    12} R ∂ x     ∂ t ²     hR

∂u       w  h2    ∂4w  1

B12     + B22  2 +   B11   4 =  (p+z)-ρ

• 12    R∂x    22 R2 12 11 ∂x4   h∂

Уравнения движения и неразрывности жидкости

1 ∂ p ∂ V 8 ν

+- V = 0,

ρ ₁ ∂ x   ∂ t R ²

∂ V 2 ∂ w

+      = 0.

∂ x R ∂ t

Уравнения движения окружающей среды

	г V 2 -(	1 5 2		Ф = о,
		v 1 2	5 1 2 ;
[v 2 - 72 (      r		-	-1 ^2г ^ = 0 х 2 5 1 J

Условия контакта между оболочкой и внешней средой w = W; оr = z; т = 0 при r = R .                        (4)

В приведенных уравнениях Bik - коэффициенты упругости, р и р1 - плотность артерии и крови; u(x, t) и w(x, t) - осевое и радиальное перемещение, p - давление жидкости на стенку сосуда; z – нормальное давление окружающей среды на оболочку сосуда; V - скорость движения крови; v - кинематическая вязкость; ф(x, r, t) и ф(x, r,t) - потенциальные функции; х1 =

' 2 G о ( 1 -Ц о ) ' ^р о ^{( 1} - ^{2 ц} о )

и х 2 =

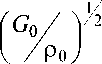
– скорость

волны расширения и волны сдвига окружающей артерию среды ( G ₀ – модуль сдвига, ц 0 - коэффициент Пуассона, р 0 - плотность).

Радиальное перемещение W ( r , x , t ) и компоненты напряжения о _r ( r , x , t ), т ( r , x , t ) среды выражаются через потенциальные функции ф , ф следующим образом:

W = дф-дф ,

5 r 5 x

2    22

° r

^{р ц} £1+ 2 х 2 р о «!-£*

1 -ц 0 5 1 ²          (d r ² 5 r 5 x _v

Решение систем уравнений (1)-(3) будем искать в виде бегущих волн:

(u, V, w,p,z,ф,ф) = (u0,V, Wo,p0,zо, фо,фо)e (mt kx), где k - волновое число, го го, + iго2; го1 - частота колебаний всей системы, го2 -коэффициент, характеризующий затухание колебания.

Удовлетворяя решение (6) уравнениям (1)-(3) с учетом условий контакта (4), для определения относительной скорости пульсовой волны получаем следующее дисперсионное уравнение :

_ ( х \        ( х ] ,    ( х ] ,    ( V ],_( V V _ V , _„ a 11 — I + a 21 — I + a 31 — I + a 41 — I + a 51 — I + a 6 —+ a 7 = 0,(7)

( c )        ( c )        ( c )        ( c )        ( c ) c го

– скорость продольной волны

где v =--скорость пульсовой волны, c = —,г k                                          V р(1 - Ц1Ц 2)

в оболочке, ц 1 , ц ₂ - коэффициенты Пуассона ортотропной оболочки, E 1 - модуль упругости оболочки,

„     6 J „2/2^2 РР 1 РР 0 Ц 0 /2

ал — c л р к +----- к

¹ г hR hm 1 -ц 0

^

J о ( mR ) 1 J 1 ( mR ) ,

5 16 iVppi a 2 — c        n , hkR a3

— c 1

f^ -^°- к ² ( 2 р v 2 + B„ ) J -mR ' - 4 v 2 fp² к 2 hm 1 - ц ₀               J 1 ( mR )      V

, ^2pp1 I D „1 2 1 , ^h /2     „B 22 П ^p1 B 11

+--- В.pк 1 +--к -p—-22---- hR J 1 I 12 I    R2      hR

где

2 n

to ²

J0, J1 - функции Бесселя первого рода нулевого и первого порядка, m2 — — - к2, v1

tor - к ².

v 2

Отметим, что уравнение (7) можно исследовать численно в зависимости от кинематической вязкости и от физико-механических и геометрических параметров как сосуда, так и тканевой среды.

В дальнейшем для получения обозримого результата упростим поставленную задачу.

Окружающую тканевую среду примем в виде упругого основания Винклера с заданным коэффициентом постели K [5]:

z — Kw , K —

—

E 0

1 + ц 0 R

Заменяя в (1) выражение нормального давления окружающей среды на оболочку сосуда через (8), представляя решение полученных уравнений через (6), получим следующее дисперсионное уравнение

—

V

к² R ²₊ 2 E R If v I ⁴ ₊ 16 V £ 1

B²^ + ^^{P1 R} + к² R²

B 11     р h

1+

V

1 -9 1 9 2

р h

c

kRh р     E 1

I v I р| -1

V c J

—

h ² к ² 1

RE 0

\

12 J ( 1 + Ц 0 ) hBn J

h ² k ⁴ R ²

+

—

г

v I ²    8 i v р 1 2 B 11 + B ₁₂

—

1 -9 1 9 2

c

kRh р

B 11

E 1

р[Л+ (9)

V c J

Г2 ⁺ В 2² 1 ^{1 +}

B 11     B 11 V

RE 0

\

(1 + Ц ) hB22 J

— 0.

Уравнение (9) дает две скорости волн: меньшая скорость соответствует волнам давления, распространяющимся в жидкости, а большая – в оболочке, с учетом влияния окружающей тканевой среды.

Численным исследованием уравнения (9) выясним влияние напряженного состояния оболочки на скорость распространения пульсовой волны.

На рисунках построены кривые изменения относительной скорости распространения волны v / c для различных отношений тканевой среды и оболочки при следующих параметрах, более или менее соответствующих действительности [5]:

B 2² — 2; R — 5; ^ 1 — 0,96; ц — 0,5; ц₂ — 0,25; ц₀ — 0,5; R — 1,4 см;

B11        h р ц — 0,035 П ; ц — vp1; р1 —1,056 г/см; c —18,5 см/с.

По оси абсцисс отложена безразмерная величина X /2 R , где X - длина волны.

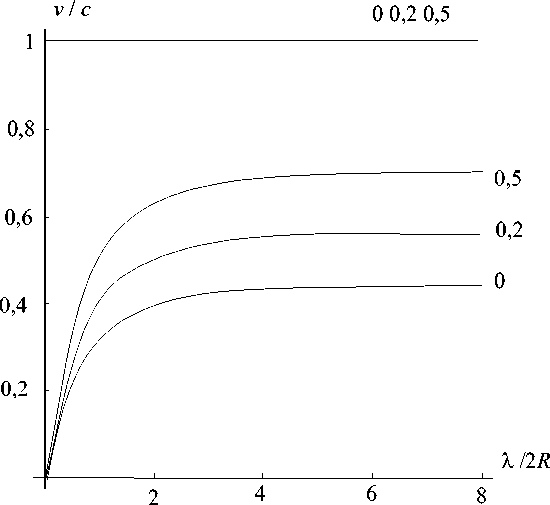
Рис. 1. Зависимость скорости распространения пульсовой волны от отношения λ /2 R

( λ – длина волны, R – радиус артерии) при различных значениях E ₀/ E ₂ ( E ₀ – модуль Юнга среды, E 2 – модуль оболочки), цифры около линий – значения E 0 / E 2 . Безмоментное напряженное состояние артерии

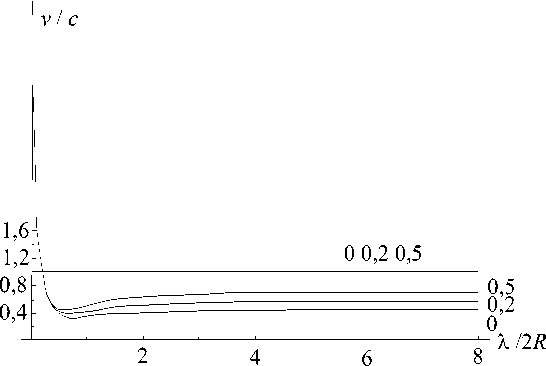
Рис. 2. Зависимость скорости распространения пульсовой волны от отношения λ /2 R

( λ – длина волны, R – радиус артерии) при различных значениях E 0 / E 2 ( E 0 – модуль Юнга среды, E ₂ – модуль оболочки), цифры около линий – значения E ₀/ E ₂. Моментное напряженное состояние артерии

Рис. 1 соответствует случаю, когда вязкость жидкости отсутствует, а для артерии принимается безмоментное напряженное состояние [5].

В этом случае получаем две скорости. Окружающая тканевая среда увеличивает значение скорости пульсовой волны, причем эта скорость увеличивается существенно с увеличением E ₀ / E ₂ , E ₂ = B ₂₂ (1 - µ ₁ µ ₂) . Большая скорость почти не изменяется и приблизительно равна единице. Цифры у линий – значения E ₀ / E ₂ .

Рис. 2 соответствует случаю моментного напряженного состояния артерии. Как и в предыдущем случае, получаются две скорости. Большая скорость почти не изменяется и приблизительно равна единице. Меньшая скорость, в отличие от безмоментного напряженного состояния, при малых значениях относительной длины волны достигает больших значений (больших, чем большая скорость). Далее при определенных значениях относительной длины волны (например λ I 2 R ≈ 0,7 при

E ₀ E ₂ = 0,2) принимает минимальное значение, затем, как и при безмоментном напряженном состоянии, увеличивается.

Проведены исследования и при наличии вязкости жидкости. В обоих случаях (безмоментное и моментное напряженное состояние артерии) поведение кривых изменений скорости распространения волн мало отличается от кривых, приведенных на рисунках 1 и 2. Вязкость жидкости незначительно влияет на скорость распространения пульсовой волны. Наличие окружающей среды приводит к уменьшению влияния вязкости жидкости [5]. Вязкость жидкости в обоих случаях приводит к тому, что волна распространяется с затуханием. Величина скорости является комплексной величиной, действительная часть которой совпадает со значением скорости распространения пульсовой волны, а мнимая часть характеризирует затухание колебаний.

Из рисунков видно также, что, начиная от X/2 R = 6, меньшая скорость распространения пульсовой волны достигает своего асимптотического значения.