О влиянии реологических и миогенных факторов на кровоток в резистивном сосуде

Сопротивление резистивных сосудов, к которым относят мелкие артерии и артериолы, определяется сосудистым тонусом и кажущейся вязкостью крови, зависящей от показателя гематокрита, распределения и свойств форменных элементов крови, вязкости плазмы, напряжения сдвига на стенке сосуда [5]. На тонус сосуда, помимо нервных и химических факторов, влияют механические стимулы – колебания трансмурального давления и напряжения сдвига на стенке сосуда [12]. Известно,

Шадрина Нажия Хабибуллаевна, к.ф.-м.н., научный сотрудник Института физиологии имени И.П. Павлова, Санкт-Петербург что ширина свободного от форменных элементов пристеночного слоя плазмы меняется с изменением напряжения сдвига на стенке сосуда [19, 28]. В свою очередь, плазменный слой влияет на транспорт оксида азота и диффузию его в стенке, а следовательно, и на регуляцию тонуса [10]. Немаловажное значение в формировании плазменного слоя имеют деформируемость и агрегируемость эритроцитов [29], влияющие и на вязкость крови. Сложные взаимосвязи сосудистых реакций и реологических факторов обсуждались не раз [10, 16], имеются единичные примеры качественного рассмотрения условий, при которых проявляется компенсирующее или усиливающее влияние пристеночного слоя на сосудистое сопротивление [7]. Тем не менее количественные оценки не производились ни экспериментально, ни теоретически.

Ранее были получены [2, 8, 9] оценки изменений радиуса и кровотока в ответ на колебания трансмурального давления (разности между давлениями на внутренней и наружной поверхности стенки сосуда) и изменения касательного напряжения сдвига на внутренней стенке сосуда. Первый из этих эффектов, известный как эффект Бейлисса, приводит к расширению сосуда при снижении трансмурального давления и сужению при увеличении давления. Эффект обусловлен зависимостью сократительной активности гладких мышц, регулируемой концентрацией свободных ионов кальция в гладкомышечных клетках, от напряжений в сосудистой стенке. Реакция на изменения напряжения сдвига, или NO-зависимая реакция, проявляется в виде увеличения/уменьшения сосудистого просвета при росте/снижении напряжения сдвига на стенке сосуда. Эта реакция вызвана выделением оксида азота (NO) эндотелиальными клетками, выстилающими изнутри сосудистую стенку, под действием сдвигового напряжения. Считается, что NO, продуцируемый эндотелием, диффундирует в гладкомышечный слой и снижает сократительную активность гладкомышечных клеток. Поскольку целью работ [2, 8, 9] было исследование роли каждой из двух сосудистых реакций в регуляции кровотока, кровь считалась ньютоновской жидкостью, зависимость вязкости крови от радиуса сосуда не учитывалась. В предлагаемой работе вводятся в рассмотрение реологические факторы, а именно зависимость кажущейся вязкости крови от радиуса (эффект Фареуса– Линдквиста) и отличие показателя гематокрита в сосуде (динамического гематокрита) от гематокрита в сливном резервуаре (эффект Фареуса). Сравнивается величина кровотока при учете и без рассмотрения двух этих эффектов.

Постановка задачи

Рассматривается течение крови в сосуде, внутренняя поверхность которого мало отличается от кругового цилиндра и слабо меняется вдоль оси. Полагается, что радиус сосуда мал по сравнению с длиной. Известно, что течение в резистивных сосудах характеризуется малыми значениями числа Рейнольдса (Re << 1) и параметра Уомерсли W = R^ ro/v <  0,5 ( R - внутренний радиус сосуда; ш - угловая частота пульсаций градиента давления; ν – кинематическая вязкость крови). Эти условия позволяют применить квазистационарные уравнения гидродинамической теории смазки для всей области потока в сосуде (см., например, [4]).

д Q дп R ²  -          п R ⁴ д p

— +----= 0, Q =----.

д x     д t                  8 n _app д x

Здесь Q – расход; x – продольная координата; t – время; η app – кажущаяся вязкость крови; p – трансмуральное давление. Далее в тексте по умолчанию под словом «давление» будет подразумеваться именно трансмуральное давление. Давление на внешней поверхности предполагается постоянным и равным, как правило, атмосферному давлению.

Предполагается, что регуляция просвета сосуда осуществляется концентрацией свободных ионов кальция в гладкомышечных клетках C m и средней концентрацией оксида азота C в гладкомышечном слое. При этом постулируется, что C m однозначным образом зависит от среднего окружного напряжения в стенке: с = pR / h ( h - толщина стенки сосуда), а скорость производства NO эндотелием пропорциональна модулю напряжения сдвига τ w на стенке.

Уравнения для радиуса и концентрации кальция имеют следующий вид [2, 9]:

Л , ^ + R = Л , dp + ( Fpas ( p) - Fact (Cm ) )(Ф( C) + 1) ,(2)

а-С^ = — Cm + *) + P^p.(3)

9 t9 t

Здесь ЛR, Лp, а, в   - постоянные; функция F (p) = Rmax - a —max0

p + a описывает зависимость статического радиуса пассивного сосуда от давления, Rmax ,R0 ,a – постоянные величины, определяемые аппроксимацией экспериментальных кривых, приведенных в работе [17]. Функция Fact (Cm ) отражает изменения радиуса активного сосуда, вызванные сокращением гладких мышц, она получена сплайн-аппроксимацией данных работы [17]. Множитель (Ф(C) +1) в уравнении (2) описывает регуляцию радиуса оксидом азота. Зависимость Ф( C) получена на основе литературных данных (см. [2]) и имеет вид Ф(C) = 0[1 + tanh(n lg( 4 C))]. Функция у(с) в (3) представляет собой сплайн-аппроксимацию результатов, представленных в работе [17] (см. [2]).

Концентрация оксида азота C находится из уравнений, описывающих радиальную диффузию NO из эндотелия. Полагается, что стенка сосуда состоит из трех концентрических слоев: эндотелия, гладкомышечного и наружного (адвентиции), ширина которых меняется при сокращении/релаксации гладкомышечных клеток. Содержимое сосуда разбивается на две области: внутреннее «ядро» с эритроцитами и наружный пристеночный слой плазмы. Уравнения диффузии записываются для каждой области внутри сосуда и его стенки:

9 C i = D i 5

91    r 9 r

5 C rⁱ

5 r

- k i C/- , i = 1, 2, ..., 5.

Здесь i = 1 (0 <  r <  R 1 ) соответствует эритроцитарному ядру, i = 2 ( R 1 <  r <  R ₂) -кольцевому плазменному слою, i = 3 ( R ₂<  r <  R 3 ) - эндотелию, i = 4 ( R 3 <  r <  R 4 ) -гладкомышечному слою, i = 5 ( R 4 <  r <  R 5 ) - адвентиции и прилегающему слою окружающей ткани шириной 6; R ₂ = R , R ₅ = R + h + 5 . На границе между областями выполняются условия непрерывности концентраций и потоков

C.(t,R,x) = Ci+1(t,Ri,x),    i = 1, ..., 4,(5)

9 C ( t , R , x )         9 C i ₄₁ ( t , R i , x )

------1-------= Di+1------5--------, i =1; 4.

9 r9 r

На границах эндотелия с плазмой крови и гладкомышечным слоем условия непрерывности потока суть

⁵ c- ⁽ t , R , x ) - D . ⁵ C + 1 ⁽ t , R , x ) =dt| , i = 2;3; t= R d p .

9r           ^{i + 1}        9r ^{1 w|               w} 2 9x

Значения параметров

Параметр	Значение	Единицы измерения	Источник
Λ R	40	c	[9]
Λ p	1,47∙10–7	м3∙с∙Н–1	[9]
a	3360,49	Н∙м–2	[9]
R*	98∙10–6	м	[9]
R max	116,4∙10–6	м	[9]
R 0	48,92∙10–6	м	[9]
θ	0,06	–	аппроксимация данных [15]
ξ	18,75∙104	м3∙моль–1	оценка по данным [15]
α	50	с	[9]
β	2,25∙10–7	моль∙с∙м–1∙Н–1	[9]
ζ	0,25∙10–9	моль∙с–1∙Н–1	см. [8]
Ζ v	8,6579∙109	Н∙с∙м–5	[8]
S w	1,112∙10–12 ( R* )2	м2	оценка по данным [17, 21]
S 3	1,21∙10–13 S w	м2	[11]
S 4	6,94∙10–13 S w	м2	[11]
D i , i = 1 ^ 3	3,3∙10–9	м2 с–1	[2]
D , , i = 4;5	8,5∙10–10	м2∙с–1	[8]
k 2	0,26	моль–1∙м3∙с–1	[18]
k 3	0,26	моль–1∙м3∙с–1	[18]
k 4	50	моль–1∙м3∙с–1	[27]
k 5	1	с–1	[26]
X 1 , X 5	1	–	[26]
X 2 , Х з	2	–	[18]
X 4	2	–	[27]

В уравнениях (4)–(7) C i , D i , k i , χ i – концентрация, коэффициент диффузии, скорость и порядок реакции NO в i- й области, D i , k i , χ i , ζ – постоянные величины, их значения приведены в таблице.

В центре сосуда выполняется условие симметрии

8 C i ( t ,0, x ) = ₀

5 r

На внешней границе r = R + h + 5 поток считается нулевым:

8 С 5 ( t , R ₅, x ) = 0 d r

Управляющий параметр C находится осреднением концентрации NO в гладкомышечном слое:

C ( t , x ) =

n ( R 2 - R ²)

2 n j 0

R ₄ ( t , x )

J C ₄( t , r , x ) rdrd ф .

R 3 ( t , x )

Условие несжимаемости стенки и ее слоев при отсутствии продольных растяжений сводится к соотношениям

S w =n[ ( R + h )² - R ² ] = const, S i =n ( R i - R i - ) = const, i = 3; 4 .          (11)

Если считать кровь ньютоновской жидкостью, то n app = const, и после задания давлений на входном p in и выходном p out концах сосуда система уравнений (1)-(11) становится замкнутой. Такая постановка задачи была изложена ранее в работе [2]. Далее давление на концах сосуда будет задаваться в следующем виде:

Pn = Pa ,  Pout = Pv — ZvQv , где pa, pv – константы, Qv и Zv – расход и сопротивление на выходе из сосуда.

При учете эффекта Фареуса–Линдквиста необходимо ввести в рассмотрение зависимость кажущейся вязкости крови от внутреннего радиуса сосуда. На основе анализа большого числа публикаций и собственных исследований течения суспензий эритроцитов в стеклянных трубках авторы работы [22] вывели эмпирические соотношения, связывающие кажущуюся вязкость крови с внутренним диаметром трубки D , показателем гематокрита в сливном резервуаре H D и вязкостью плазмы η pl :

^П rel

app n pl

^{1 + ( n} rel ,0,45

^- 1)

(1 — H d ) M — 1 (1 - 0,45) ^M - 1

Здесь

Пrel,0,45 = 220 exp(-1,3D) + 3,2 - 2,44 exp(-0,06D) ,(14)

M = (0,8 + exp(-0,0753D )(-1 +-----——) +-----——.

1 + 10 ^{- 11} D ¹²    1 + 10 ^{- 11} D ¹²

Той же группой авторов на основе анализа литературных данных была получена эмпирическая формула для вычисления динамического гематокрита H T [23]:

-^ = HD + (1 - HD )(1 +1,7 exp(-0,35 D) - 0,6 exp(-0,01D).(16)

HD app

П о

П о

R 1

П с

R

+1 -

R 1

R

- 1

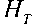
H C

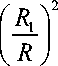
^HD '\._:: к ^f R_ ) + 2 ^f R_ ) 1 _(R ) Н с   П о   п С I R ) I R ) I R )

Решение получено при условии, что скорости и касательные напряжения на границе между слоями непрерывны. Показатели гематокрита H D и H T определяются соотношениями

RR

HD = Q J rht (r) u (r) dr , HT = R J rht (r) dr , где ht (r), u(r) – локальные значения показателя гематокрита и скорости.

Выражение для вязкости п С получено в работе [24] из эмпирической формулы (13) в предположении, что п С = П _app при D ^ 0:

п ,.. (1 - Н с Г^0,8 - 1

1 + 2, 2                 л о • пpl           (1 - 0,45)-0,8 -1

Воспользуемся также предложенным авторами работы [24] способом учета неоднократно описанных в экспериментальных [19, 20, 28] и теоретических работах [7, 13] колебаний ширины плазменного слоя. Поскольку флуктуационные радиальные смещения эритроцитов вызывают дополнительную диссипацию энергии вблизи стенки, полагается, что п ₀ больше вязкости плазмы и является функцией толщины пристеночного слоя и показателя гематокрита.

Таким образом, течение крови в резистивном сосуде с учетом эффектов Фареуса и Фареуса–Линдквиста описывается уравнениями (1)–(4), (10), (11), (13)–(20) и граничными условиями (5)-(9), (12). Начальные условия при t = 0 берутся из экспериментальных данных работы [17].

Методы решения и значения параметров

Система уравнений, описывающих течение ньютоновской жидкости, решалась численно описанным ранее методом [2, 9]. После перехода к безразмерным переменным и уравнениям в конечных разностях производилась линеаризация последних. Затем для каждого момента времени t = t j из конечно-разностных аналогов уравнений (1–3) и условия (12) находились значения p ( t j , x ), R ( t j , x ), C m ( t j , x ) при C = C ( x , t j_ i ) из предыдущего временного слоя. После исключения из уравнений переменных R ( t j , x ), C m ( t j , x ) вычислялись итерации p ( x , t j ) методом прогонки. Итерации проводились до тех пор, пока модуль разности между s- й и ( s + 1)-й итерациями p ( t j , x ) не оказывался меньше 10 - 7 , затем из линейных соотношений находились R ( t j , x ), C m ( t j , x ). Для нахождения C ( t j , x ) решалась задача о радиальной диффузии (4–9), (11).

После перехода к новым переменным т = t, p = r I R1, i = 1; p = (r - Ri-1)I( Ri - Ri-1), i = 2; 3; 4; p = (r - R4)I 5, i = 5, где 0 < p < 1, методом параметрической прогонки [3] в каждой из пяти областей определялась концентрация оксида азота Ci(т, р, x), т = tj, и по формуле (10) вычислялся параметр C(tj, x).

При рассмотрении неньютоновских свойств крови сначала для каждого момента времени t = t j описанным выше методом вычислялись p ( t j , x ), R ( t j , x ), C m ( t j , x ) при C = C ( x , t j- 1 ), n _app ( x , t j- 1 ). Зная R ( t j , x ), из эмпирических соотношений (13-16) определяли n _app ( x , t j ), H t ( x , t j ) и решали уравнения (17-20) относительно R 1 ( t j , x ), Н С ( t j , x ), n ₀ и П _c • Уравнения (17-20) можно свести к одному неявному уравнению относительно переменной H С ( t j , x ):

Hc = Y (Нс ),(21)

Y ( Н с ) =

_____________________ 2П app H_T I? n app - ^Н n C ( Н с ) +   n app - ^Hd n C ( H c )   - 4 n app ( H_d I H t - 2 ) -n с ( H c )

Ht           yv Ht7

Здесь

Пс(Hc ) = npi [1 - A + A (1 - Hc)-“]. A =      2'2.

( 1 - 0,45 ) - 1

Уравнение (21) решается методом итераций. Оценки показали, что отображение H_c 2 = Y ( Н_с 1 ) является сжимающим, т.е. решение удовлетворяет критерию единственности [1]. После нахождения Н с определяются R 1 ( t j , x ), n ₀ и n С и рассматриваются уравнения диффузии (4–9), (11) для момента времени t j с использованием вычисленных для t = t_j значений R 1 ( t j , x ), Н_С ( t j , x ). Последний параметр влияет на коэффициент взаимодействия NO с гемоглобином в области 1 (0 <  r <  R 1 ).

Счет осуществлялся в среде Turbo Pascal. Полагалось, что npi = 0,0158 П, Hd = 0,45, длина сосуда l = 20R*, где R* - радиус пассивного сосуда при p = 60 мм рт. ст. Параметр к 1, характеризующий скорость реакции NO в центральной части сосуда, пропорционален HС, скорости взаимодействия NO c эритроцитарным гемоглобином и концентрации гемоглобина в одном эритроците. Если принять, что при Нс = 0,45 к1 = 1230 с-1 [14], то при изменении динамического гематокрита к 1 (с-1) пересчитывается по формуле к ,= 1230-Нс-.

¹        0,45

Значения остальных параметров приведены в таблице. Для описания свойств сосудистой стенки использовались параметры и функциональные зависимости, полученные в экспериментах на мелких мозговых артериях крыс [17]. При вычислениях задавалось p a , полагалось, что p a - p v = 1 мм рт. ст., Z v = const.

Результаты вычислений представлены в виде относительных изменений сравниваемых величин, выраженных в процентах. Расчеты проводились для точки, равноудаленной от концов сосуда.

Результаты и их обсуждение

На рис. 1 представлена зависимость относительных изменений радиуса, расхода и кажущейся вязкости крови, вычисленных для «бейлиссовского» сосуда с учетом реологических эффектов, по сравнению с их значениями, полученными без рассмотрения реологических факторов, от входного давления. Относительные изменения каждого параметра Y вычисляются как A Y = ( Y ⁺- Y - )/ Y - - 100%, где Y ⁺ и Y - - соответственно значения параметра Y , вычисленные с учетом эффектов Фареуса и Фареуса–Линдквиста и без их рассмотрения. В случае, когда реологические эффекты не рассматривались, кажущаяся вязкость крови бралась равной среднему в рассмотренном диапазоне p in значению вязкости, вычисленной с учетом этих эффектов.

Реологические эффекты практически не влияют на радиус сосуда: A R = 0 во всем рассмотренном диапазоне давлений на входе в сосуд (см. рис. 1, линия 1 ). Поскольку для приближения к физиологическим условиям разность давлений на концах сосуда бралась много меньше входного давления, изменения радиуса при переходе от статического режима к динамическому практически отсутствуют. Внутренний радиус сосуда главным образом определяется входным давлением, и его зависимость от p a аналогична статической кривой на рис. 2. Вклад эффекта Фареуса– Линдквиста в изменения кажущейся вязкости и расхода зависит от входного давления (см. рис. 1, линии 2 , 3 ). Если сравнить график функции Ap _app ( p a ) (см. рис. 1, линия 3 ) и зависимость статического радиуса активного сосуда от давления (см. рис. 2), то обнаруживается положительная корреляция относительных изменений вязкости и статического радиуса. В результате зависимость относительных изменений расхода от давления имеет противоположную направленность (см. рис. 1, линия 2 ). Тот факт, что эффект Фареуса–Линдквиста не приводит к видимым изменениям внутреннего радиуса, но вызывает изменения кажущейся вязкости, можно объяснить высокой чувствительностью кажущейся вязкости крови даже к очень малым колебаниям диаметра.

Аналогичная картина относительных изменений Q и р _app в зависимости от p a следует и из расчетов для сосуда с обеими механогенными реакциями (рис. 3). Как и для сосуда с реакцией Бейлисса, сначала производились вычисления с учетом реологических факторов. Кажущаяся вязкость при отсутствии реологических эффектов определялась осреднением значений кажущейся вязкости, вычисленных

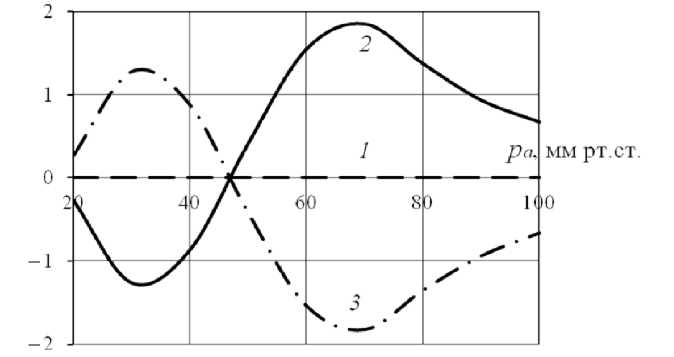
Рис. 1. Зависимость относительных изменений R (линия 1 ), Q ( 2 ) и η _a pp ( 3 ) за счет эффекта Фареуса–Линдквиста от входного давления в сосуде с реакцией Бейлисса

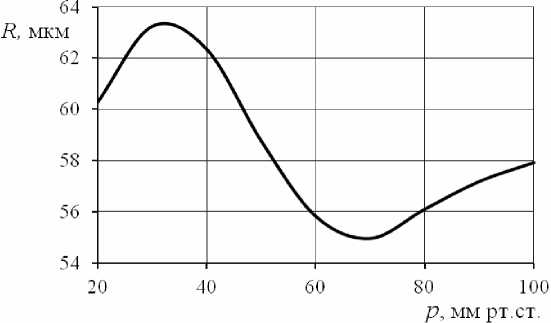
Рис. 2. Статическая зависимость внутреннего радиуса сосуда от трансмурального давления для мелкой мозговой артерии крысы (по данным [17])

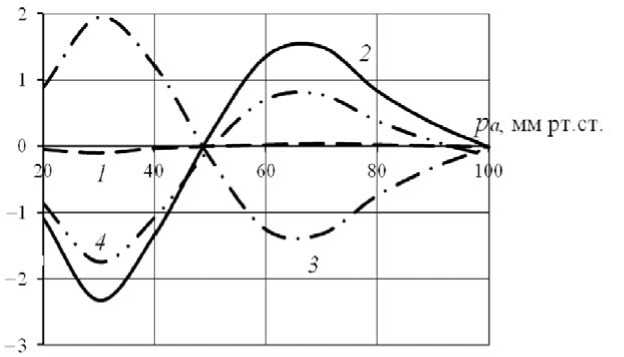
Рис. 3. Зависимость относительных изменений R (линия 1), Q (2), ηapp (3) и C (4), вызванных реологическими факторами, от входного давления в сосуде с обеими реакциями в рассматриваемом диапазоне входных давлений с учетом реологических факторов и обеих реакций на механические стимулы. Если для зависимостей ΔQ(pa) и ∆ηapp (pa) на рис. 1 и 3 наблюдается лишь некоторое количественное отличие, то зависимость ∆R(pa) отличается качественно. Наиболее заметно различие проявляется при низких значениях давления: за счет реологических факторов вслед за уменьшением концентрации NO происходит снижение радиуса. В диапазоне 40–90 мм рт. ст. наличие реологических эффектов приводит к меньшим изменениям ΔC и менее заметным изменениям радиуса. Следует отметить, что изменения радиуса достаточно малы: в рассмотренных сосудах максимальное изменение, обусловленное реологическими факторами, составляет 0,1%. Если в сосуде с реакцией Бейлисса относительные изменения расхода за счет реологических эффектов связаны с изменениями кажущейся вязкости, то при наличии NO-зависимой реакции относительные изменения расхода обусловлены изменениями как радиуса, так и ηapp . Количественные оценки показали, что относительные изменения расхода по абсолютной величине не превышают 2% в сосуде с реакцией Бейлисса и 2,5% в сосуде с двумя реакциями.

В пассивном сосуде при отсутствии активации гладкомышечных клеток зависимость относительных изменений кажущейся вязкости, вызванных эффектом Фареуса–Линдквиста, от входного давления имеет монотонный характер: с ростом давления кажущаяся вязкость, как и статический радиус, увеличивается (рис. 4), кровоток, соответственно, снижается. Диапазон изменений ΔQ в пассивном и активном сосудах практически совпадает. Как и в сосуде с реакцией Бейлисса, реологические эффекты не влияют на радиус пассивного сосуда.

Сопоставление внутреннего радиуса и кровотока в сосуде с реакцией Бейлисса и пассивном сосуде, а также в сосуде с обеими реакциями и «бейлиссовском» сосуде при тех же условиях на концах сосуда проводилось с помощью следующих параметров:

A R B _ pas = ( R b - R p„ ) / R pas ' 100% - A Q b _ , = ( Q b — Q . ) / Q p. -100% ,

AR NO _ B =( Rno + B - Rb ) / Rb '100%, AQno _ B =( Qno + B - Qb ) / Qb-100%, где нижние индексы «pas», «B», «NO+B» соответствуют пассивному, «бейлиссовскому» и сосуду с обеими реакциями.

На рис. 5 показаны изменения A R_{B pas} , A Q_{b pas} в зависимости от давления на входе в сосуд, полученные при вычислениях с учетом (линии 1 , 2 ) и без учета (линии 3 , 4 ) реологических эффектов. Снижение радиуса сосуда с активными миоцитами относительно радиуса пассивного сосуда (рис. 5, линии 1 , 3 ) составляет от 24 до 44%,

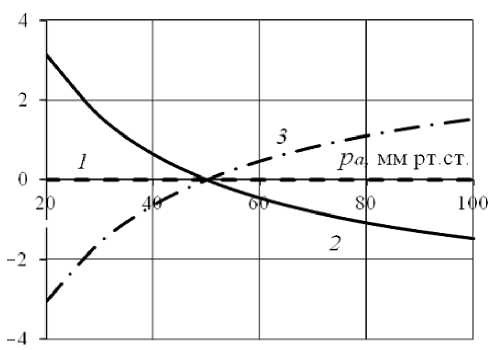
Рис. 4. Зависимость относительных изменений R (линия 1 ), Q ( 2 ) и η app ( 3 ), вызванных эффектом Фареуса–Линдкиста, от входного давления в пассивном сосуде

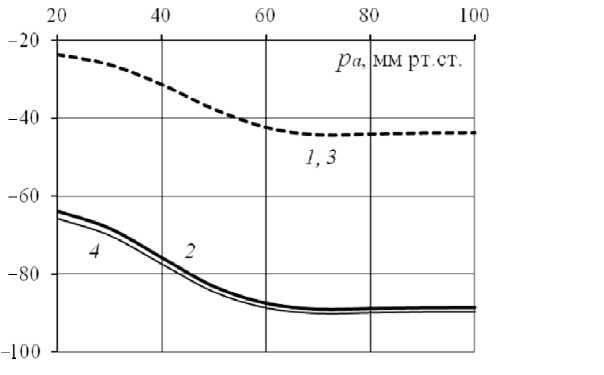
Рис. 5. Изменения R (линии 1 , 3 ) и Q ( 2 , 4 ) в «бейлиссовском» сосуде относительно тех же параметров в пассивном сосуде, вычисленные с учетом ( 1 , 2 ) и без учета ( 3 , 4 ) реологических факторов

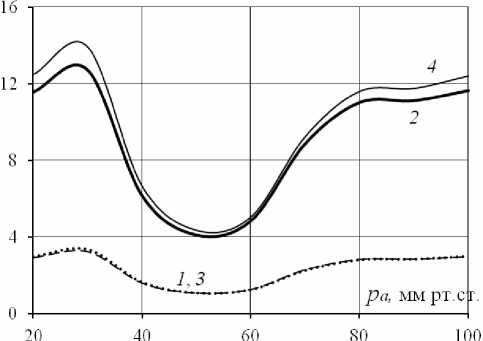
Рис. 6. Изменения R (1, 3) и Q (2, 4) в сосуде с двумя реакциями относительно тех же параметров в «бейлиссовским» сосуде, вычисленные с учетом (1, 2) и без учета (3, 4) реологических факторов а снижение кровотока может достигать 90% (см. рис. 3, линии 2, 4). Реологические факторы не влияют на ∆RB_pas , но уменьшают различие расходов в «бейлиссовском» и пассивном сосудах, это уменьшение не превышает 2%.

В сосуде с обеими реакциями при тех же условиях на концах сосуда радиус и расход увеличиваются по сравнению с «бейлиссовским» сосудом (рис. 6). Если максимальное увеличение радиуса составляет менее 4%, то рост расхода может доходить до 14%. Отметим явно выраженную немонотонность зависимостей ∆ R _{NO B} , ∆ Q_{NO _ B} от входного давления по сравнению с параметрами ∆ R_{B _ pas} , ∆ Q_{B _ pas} . Снижение ∆ R _{NO B} и ∆ Q_{NO B} происходит в диапазоне давлений, соответствующем падающему участку статической зависимости R ( p ). Как и на рис. 5, наличие эффектов Фареуса и Фареуса–Линдквиста заметно не сказывается на величине ∆ R _{NO B} (линии 1 и 3 на рис. 6 совпадают) и приводит к небольшому снижению ∆ Q_{NO B} , причем величина этого снижения зависит от давления и не превышает 2%.

Расчеты для мелкой мозговой артерии крысы показали, что при тех же условиях на концах сосуда радиус и кровоток в активном сосуде на десятки процентов меньше, чем в пассивном, на всем исследованном диапазоне давлений, причем это различие увеличивается с ростом входного давления (см. рис. 5). При давлении выше 60 мм рт. ст. расход снижается почти на 90%. Реологические факторы на эти различия практически не влияют. Рост кровотока за счет NO-зависимой реакции в активном сосуде может превысить 12%, эта величина зависит от давления и, в конечном счете, при неизменной разности давлений на концах сосуда определяется уровнем сосудистого тонуса, что соответствует выводам экспериментальных работ [6, 25]. Вклад реологических факторов также зависит от давления, но он относительно мал. Эти факторы уменьшают снижение кровотока в «бейлиссовском» сосуде по сравнению с пассивным и повышают его в сосуде с двумя реакциями по сравнению с «бейлиссовским».

Степень влияния сосудистых реакций существенным образом зависит от индивидуальных свойств сосуда: от его положения в сосудистой иерархии, свойств его стенки, вида животного. Поэтому количественные оценки могут быть различны для разных сосудов. Все вычисления выполнены применительно к мелким мозговым артериям. Рассмотрение именно этих сосудов было обусловлено тем, что только для этих сосудов удалось найти максимальный набор необходимых экспериментальных данных.

Заключение

Рассмотрено изменение кровотока в одиночном сосуде под действием механических (трансмурального давления и напряжения сдвига на сосудистой стенке) и реологических факторов (эффектов Фареуса и Фареуса–Линдквиста). Оценки показали существенное влияние сосудистых реакций на сопротивление: снижение кровотока за счет реакции Бейлисса может достигать 90%, NO-зависимая реакция приводит к повышению кровотока, которое может доходить до 14% относительно кровотока в «бейлиссовском» сосуде. Изменение кровотока за счет рассмотренных реологических факторов не превышает 2,5%. Оценки сделаны применительно к мелким мозговым артериям. Степень влияния сосудистых реакций существенным образом зависит от индивидуальных свойств сосуда, поэтому количественные оценки для разных сосудов могут отличаться.