О воздействии Солнца на сейсмичность Земли

In solar-terrestrial physics, the problem of the effect of solar and geomagnetic activities on dynamic processes in the earth’s crust is of particular interest. This problem has been discussed for more than a century, but there is no generally accepted opinion on the reality of the influence of space factors on earthquake activity so far. There is an extensive literature on this subject. We use here only some recent publications [Husamiddinov, 2000; Haya-kawa, 2001; Duma, Ruzhin, 2003; Zakrzhevskaya, Sobolev, 2004; Sobisevich, Kanonidi, Sobisevich, 2010 ; Masci, 2011; Adushkin et al., 2012; Guglielmi, Zotov, 2012; Schekotov, 2012; Buchachenko, 2014, 2019; Guglielmi et al., 2015; Tarasov, 2019].

The difficulty of the problem lies in the fact that until recently physical mechanisms of effective influence of rather weak fields of cosmic origin on powerful tectonic processes have not been known. It seems possible that geomagnetic variations have an effect on rocks, e.g., eddy currents, induced in the earth’s crust by the alternating magnetic field, lead to additional heating of rocks [Fainberg et al., 2004], although it is not clear how such a slight heating affects the probability of the occurrence of an earthquake. The action may also be force, but pon-deromotive forces cause only fairly weak stresses and strains in the crust [Guglielmi, 1992]. Macroscopic mechanisms — thermal and power — are likely to be ineffective in this case.

This work has been stimulated by new ideas put forward in [Buchachenko, 2014, 2019]. They are based on the notion of in-situ magnetoplasticity of rocks, i.e. a change in plasticity of rocks under the effect of the alternating magnetic field of natural or artificial origin, which leads to a noticeable change in seismic activity. In Section 1 of this paper, we put forward two methods for numerical description of global seismicity. Section 2 analyzes the relationship between the global daily seismicity and solar activity, characterized by Wolf numbers. Section 3 discusses prospects for further research using these methods.

METHODS OF DESCRIBING GLOBAL SEISMICITY

We use Wolf numbers W to characterize solar activity [ form/]. In addition to this, we should select an index of Earth’s seismic activity. We propose two methods of describing the global seismicity. Both the methods are based on the notion of earthquake ensemble and use data from a worldwide catalog of earthquakes such as USGS [].

For the ensemble of earthquakes occurring over a certain period of time, we introduce a statistical sum Z by analogy with Zustandssumme, known in statistical physics:

Z = E H j ^ex p (^- n M j ) •

The period is selected according to the research objective, but it should not be too short because Formula (1) is statistic. The index j = 1, 2, 3, ... numbers earthquakes recorded in the catalog for the selected period. M j is the earthquake magnitude listed in the catalog with the number j . The Heaviside symbol H j takes on values of 0 if M j < M 0 and 1 if M j ≥ M 0 . Below, we describe the choice of the magnitude M 0 and the parameter η.

Through Z , the entropy

5 = In Z + n< M >                       (2)

and the average planetary magnitude (APM) of earthquakes are expressed

< M > =-

d In Z d n

As already mentioned, the earthquake ensemble is formed from data from a particular global catalog (e.g., the USGS catalog). The probability of earthquakes with Mi is defined as P = v H I V v H. , where v, is the fre- j             j   jj     jj         j

This is an open access article under the CC BY-NC-ND license

quency of earthquakes with the said magnitude. It is understandable that E p = 1. Choose M 0 so that at M j > M 0

the Gutenberg—Richter law is true [Kasahara, 1985]. In this case,

P j = Z ^{- 1}exp ( - n M j' ) .                           (4)

Formulas (1)–(3) take the conceptual meaning if η= b ln10, where b is the known parameter of Gutenberg— Richter distribution. It is important that the formulas for the statistical sum, APM, and earthquake ensemble entropy are similar to those used in theoretical physics [Landau, Lifshitz, 2005].

Given an alternative approach to the description of Earth’s seismicity, we use the classical formula logE=A+BM.                              (5)

Here A =4.8, B =1.5 if E is expressed in joules. Formula (5) relates the magnitude M on the Richter scale to the energy E of a particular earthquake [Richter, 1958]. Let our ensemble include earthquakes that occurred per day [Guglielmi, Klain, 2019]. Find the average energy of earthquakes and from (5) determine the global daily magnitude (GDM):

M_e = 1ln g _β

E H j exP ( ^в M j )

E H j

where β= B ln10. It is evident that GDM formally and substantially differs from APM.

STATISTICAL RELATIONSHIP BETWEEN GDMAND WOLF NUMBERS

Both the proposed methods are suitable for studying the effect of space factors on seismicity. The first method provides a set of numerical characteristics of seismicity. When calculating Z and other statistical parameters, a hard lower bound is, however, set on the earthquake magnitude. The second method allows us to flexibly vary the lower bound, but provides only one numerical characteristic of seismicity, namely GDM. In this paper, we confine our analysis to a possible relationship between GDM and daily average Wolf numbers W .

Figure 1 gives insight into M g variations over the 20-year period as derived from USGS data for M 0 =1, whereas Figure 2 shows the distribution of the events by M g . We can see that the representative part of the distribution satisfies the Gutenberg—Richter law [Kasahara, 1985]

log v = a - bM ,       (7)

where a = 8.9, b =1.1.

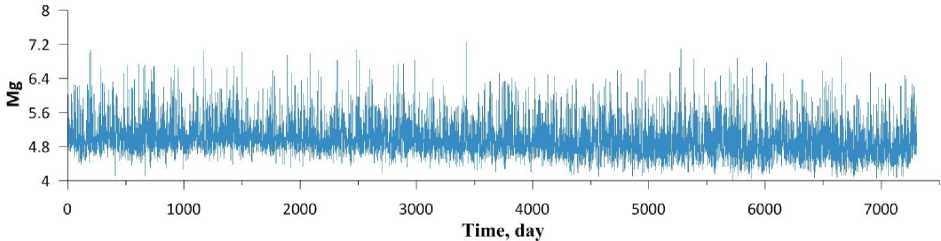
Figure 1 . Series of GDM from January 01, 1980 to December 31, 1999

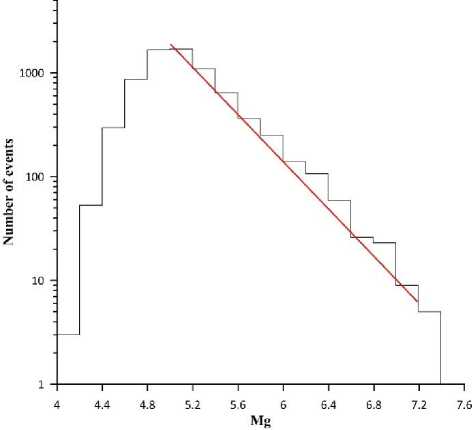
Figure 2. Frequency distribution of events by GDM

As an indicator of solar activity we have taken daily Wolf numbers W . In total, 7300 pairs of M g and W have been obtained. The spread of points reflecting the possible statistical relationship between M g and W is shown in Figure 3. The overall picture of the distribution of the points indicates that even if there is a relationship between M g and W , first it is weak and second it is rather complex. Even a weak relationship of this kind is, however, of great interest from the standpoint of solar-terrestrial physics, therefore we give another argument that the relationship between M g and W does exist.

From 7300 events, we have identified two subsets forming the lower and upper sextiles S n . Each subset contains 1217 pairs of M g and W , the lower sextile corresponding to small M g ; the upper one, to large M g . Average Wolf numbers W for days with low and high seismic activity are shown in Figure 4. Average Wolf numbers W =3.6±2 and W =104.1±2. The difference between the average W is 10.5. It is easy to show that the three sigma rule is more than adequate, therefore the relationship between M g and W is valid at a high level of statistical significance.

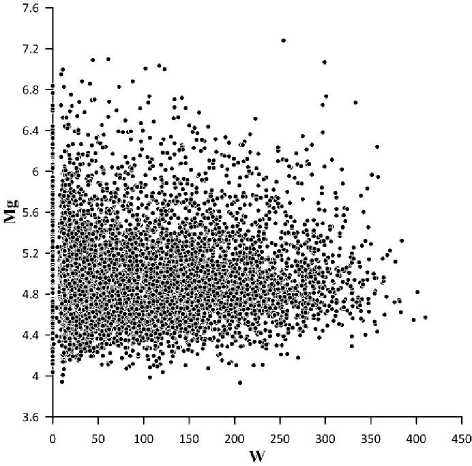
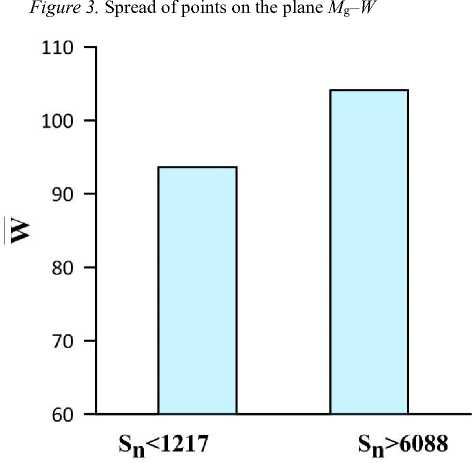
Figure 4. Average Wolf numbers for days with weak and strong seismic activity (left and right columns respectively)

DISCUSSION

The statistical sum Z of the earthquake ensemble provides information on seismic activity. Only the future will, however, show whether this yields tangible results in a particular analysis of global seismicity or not. The experimental study of terrestrial and space factors affecting earthquake activity is quite a complicated task. We plan to use Z to further clarify this problem.

In particular, we assume that it would be useful to examine fluctuations of the planetary magnitude

2     d ²ln Z

< ( ⁵ M ) >=                                (8)

dn

In a certain approximation, Earth can be considered as an autonomous dynamic system. The experience of experimental and theoretical study of autonomous systems gained in statistical radiophysics indicates that the distribution of fluctuations contains important information about the internal structure and functioning of the system under study [Rytov, 1976].

In this paper, we have used another index of seismicity, namely the global daily magnitude M g , to obtain a statistically valid answer to the question whether variable solar activity has an effect on Earth’s seismicity or not. We have found that M g varies with time within a fairly wide range (see Figure 1). Undoubtedly, the main cause of these variations is non-equilibrium processes in the inner layers of the planet. Nevertheless, we have shown that certain M g variations are determined by solar activity. No matter how small is their number, the experimental study of such variations is of interest from the standpoint of earthquake physics.

The proposed approach to the numerical description of seismicity may be useful for studying space factors affecting earthquake activity. Of particular interest is the statistical study of the relationship between numerical parameters of the planetary seismicity and Dst variations of the geomagnetic field. In the light of new ideas about magnetoplasticity of rocks [Buchachenko, 2014, 2019], we can expect interesting results.

CONCLUSION

To identify the possible relationship between earthquakes and solar activity, we have proposed two methods for numerical description of planetary seismicity. One of the methods makes it possible to calculate the statistical sum Z of the earthquake ensemble. Through Z , the entropy, average planetary magnitude, and magnitude fluctuations are expressed. At the same time, however, earthquakes should be specially selected: the distribution of selected events by magnitude must obey the Gutenberg— Richter law. The second method does not contain the said limitation, but it allows us to calculate only one numerical parameter, namely the global daily magnitude M g . We have calculated M g over the 20-year period from 1980 to 1999. The comparison between the obtained values of M g and Wolf numbers W has revealed the effect of the Sun on earthquake activity at a statistically significant level.

We express our gratitude to A.L. Buchachenko, A.D. Zavyalov, O.D. Zotov, and A.S. Potapov for their interest in this work. The work was carried out under RFBR project 18-05-00096, RAS Presidium program No. 12, project KP19-27 of the Ministry of Education and Science of the Russian Federation, as well as under the program of State tasks of The Schmidt Institute of Physics of the Earth of the Russian Academy of Sciences.