О возможной динамике в модели расчета матрицы корреспонденций (А .Дж. Вильсона)

После работ ряда крупных биологов первой половины прошлого века, а также работ Е.Т. Джейнса (конца 50-х годов XX века) [1], А.Дж. Вильсона (конца 60-х годов ХХ века) [2], И. Пригожина с коллегами, Г. Хакена (70-е годы XX века) [3, 4] в литературе достаточно прочно укрепилась концепция о плодотворности перенесения термодинамического формализма (см., например, [5--14] и цитированную там литературу) на различные макросистемы (в частности, встречающиеся в экономике, биологии, социальной сфере [2--4; 15--24]). В России систематические исследования в этом направлении были предприняты Л.Н. Розоноэром в начале 1970-х [25] (см. также [26-- 34] и цитированную там литературу). Упомянутая концепция часто используется для нахождения равновесия макросистемы. А именно, по аналогии с феноменологической термодинамикой вводится вероятностное распределение на множестве состояний, в которых может пребывать макросистема. Такое распределение может, например, совпадать с инвариантной мерой эргодической динамической системы, порождающей рассматриваемую макросистему [11], или с финальным (равным стацио- нарному) распределением эргодического (например, марковского) случайного процесса, порождающего рассматриваемую макросистему [35--40]. Если размерность макросистемы увеличивается, то, как правило, распределение сосредотачивается в окрестности наиболее вероятного макросо-стояния7. Таким образом, с ростом времени наблюдения за макросистемой и размерности макросистемы следует ожидать нахождения макросистемы с большой вероятностью в малой окрестности наиболее вероятного макросостояния вне зависимости от того, в каком состоянии макросистема находилась сначала (иначе говоря, большую часть времени (иногда, и просто, на больших временах) макросистема будет пребывать в малой окрестности наиболее вероятного макросостояния). Естественно поэтому под равновесием макросистемы понимать наиболее вероятное макросостояние. Задача нахождения наиболее вероятного макросостояния часто сводится (асимптотически по размерности системы) к задаче максимизации энтропийно подобного функционала при ограничениях (в термодинамике таким образом можно получить статистики Больцмана, Ферми–Дирака, Бозе–Эйнштейна [1, 5]). Подробнее о приложениях этой концепции см., например, [1, 2, 30, 33; 41--45]. 8

II. Возможная динамика, приводящая в асимптотике (по времени) к статической модели А.Дж. Вильсона расчёта матрицы корреспонденций

Рассмотрим для начала более простой пример, иллюстрирующий формализм, описанный во введении.

Пример 1 (кинетика социального неравенства [23, 46]). В городе живет N ^ 1 (например, 10 000) пронумерованных жителей. У каждого i -го жителя есть в начальный (нулевой) момент времени целое (неотрицательное) количество рублей s i (0) (монетками, достоинством в один рубль). Со временем пронумерованные жители (количество которых не изменяется, так же как и суммарное количество рублей) случайно разыгрывают свое имущество. Пусть в момент времени t ^ 0 r -й житель имеет k рублей, а l -й житель — m рублей. Тогда p k _; m ( t )Д t + o (Д t ) есть вероятность того, что жители с номерами r и l (1 ^ r < l ^ N ) встретятся и попробуют разыграть один рубль по следующему правилу: с вероятностью 1 / 2 житель с большим номером отдаёт 1 рубль (если, конечно, он не банкрот) жителю с меньшим номером и с вероятностью 1 / 2 наоборот. Будем считать, что P k _; m ( t ) = kN - ¹ ( к >  0). При этом «в среднем» в единицу времени осуществляется kN/ 2 встреч, т. е., скажем, при к = 1 в единицу времени каждый житель с вероятностью, большей 1 / 2, с кем-то должен встретиться. Приблизительно такую постановку задачи в конце XVIII века предложил известный итальянский экономист Вильфредо Парето, чтобы объяснить социальное неравенство.

Пусть c s ( t ) — доля жителей города, имеющих ровно s рублей в момент времени t (заметим, что c _s ( t ) — случайная величина). Пусть

N

S = Esi (0), s= N i =1

Тогда по эргодической теореме для конечных однородных марковских цепей (см. [18, 19; 35 -- 38] и упражнение ниже): ⁹

V q = 0, ..., S 3 Xq > 0, Tq = O(N) : V t > Tq ^

P

C s ( t ) Ce ^{- s/}s

λ q

VN,

s = 0, ..., q^ > 0,999 ,

где C определяется из условия нормировки:

S

E Ce-s/ = 1, s=0

то есть C

.

—

s

Скорость сходимости оценивается сверху, исходя из оценок в доказательстве эргодической теоремы для однородных марковских цепей с конечным числом состояний. ¹⁰ Как показывают численные эксперименты, оценка O( N ) точная. Так, если в городе 10 000 жителей и единица времени — день, то при начальном «социальном равенстве» с вероятностью, близкой к единице, через 20–30 лет (при к = 1) установится «социальное неравенство». Заметим, что описанный выше случайный процесс обратим во времени. Однако наблюдается необратимая динамика c s ( t ). Но в таком случае можно удивляться также и тому, что газ, собранный в начальный момент в одной половине сосуда, с течением времени равномерно распределится по сосуду.

Приведем отчасти схожую постановку задачи (та же самая мера будет концентрироваться), восходящую к В.П. Маслову [33]. Ниже приведен фрагмент его интервью 2009 года, посвященного объяснению финансового кризиса 2008 г.

В.П. Маслов: — Поясню на знаменитом трюке Коровьева-Фагота. Помните булгаковского героя, который разбрасывал в варьете червонцы? Понятно, что кому-то досталось больше купюр, кому-то меньше, а кто-то вообще остался ни с чем. Вопрос: если купюр миллион, то сколько должно быть зрителей, чтобы ни один не остался без банкноты? Вроде очень неопределенная задача, не имеющая однозначного решения. И тем не менее ответ

есть: примерно квадратный корень из миллиона, то есть тысяча зрителей.

Точнее говоря, как следует из вышенаписанно-го, с вероятностью, близкой к 1, доля банкротов будет равна примерно 1 /s ~ 0 , 001, поскольку по условию s N = S = 10 ⁶ и N ~ SS . Поэтому количество банкротов с вероятностью, близкой к 1, незначительно отличается от N/s ~ 1.

Пример 2 (модель расчета матрицы корреспонденций [2]). В некотором городе имеется n районов, L i >  0 — число жителей i -го района, W j >  0 — число работающих в j -м районе (число рабочих мест), X ij ( t ) > 0 — число жителей, живущих в i -м районе и работающих в j -м в момент времени t ^ 0. Со временем пронумерованные жители (количество которых не меняется ¹¹ и равно N = 2 i =i L i = ^j w W j ) меняют места жительства (квартиры). Считается, что отмеченные изменения могут происходить только за счёт обмена квартирами, то есть

n

X ij ( t ) > 0 , ^X ij ( t ) = L i , j =i n

E X ij ( t ) = W j , i, j = 1 ,...,n.        (А)

i =1

Пусть в момент времени t ^ 0 r-й житель живет в k-м районе и работает в m-м, а l-й житель живет в p-м районе и работает в q-м. Тогда pL m.p q (t)Дt+o(Дt) есть вероятность того, что жители с номерами r и l (1 ^ r < l ^ N) поменяются квартирами в промежутке времени (t,t+Дt). Естественно считать, что вероятность в единицу времени обмена местами жительства зависит только от мест проживания и работы обменивающихся.

Например, можно считать, что время, потраченное в пути от района i до района j , есть t ij ^ 0 (вместо t ij в приводимую ниже формулу также осмысленно подставлять l ij ^ 0 — расстояние от района i до района j ), а

L pk,m; p,q

( t ) =

= pLN 1 exp(Y • (tkm + tpq - (tpm + tkq))/2) > 0, где pL > 0, y > 0. Тогда по эргодической теореме для конечных однородных марковских цепей (см. [18, 19; 35--38]):

V {X ij УП^ j =1 G (А) -

— lim P(xij(t) = xij, i, j = 1, ..., n) = t→∞ n,n

= Z~1 П exp(—YtijXij) • (Xij!)“1 def def

^{p ( { X} ij ^} iⁿ = ^,n 1 ,j =1 ^{) ,}

где статсумма Z находится из условия нормировки получившейся пуассоновской вероятностной меры [50]. Распределение p ( {X ij У П У П j ₌₁ ) на множестве (A) сконцентрировано при N ^ 1 (см. ниже) в окрестности наиболее вероятного значения

{xj}П=1 j=1, которое находится, как решение зада чи энтропийно линейного программирования: 12

n,n                       n,n

У^ xij ln(xij/e)+ Y E tijXij —

— min .

{ X ij H j = 1 € ( A )

Решение задачи (1) можно представить как

xij = exp( — 1 — XL — XW — Ytij), где множители Лагранжа (двойственные переменные) {XL}n=1 и {XW}n=1 определяются из равенств системы (A). На практике мы имеем информацию о {Li,Wi}'=1 и {tijУ^П j=1. Решив задачу (A), мы найдем

{X km ( {L i^ W i } n =1 ; {t ij } '' j = 1 ) } П =1 ,m =1 .

Перейдем теперь к ченного стационарного ятностей p ( {x ij y n l n l j ₌₁ ) {x ij } ' = 'j =1 € ( A ). Если ¹³

исследованию полураспределения верона макросостояниях

N — na +1, Li,Wj — na (a > 1), n » 1,

V i, j = 1 , ..., n — t ij = т >  0 , то распределение вероятностей p ( {x ij } _i ⁿ ₌ ^,n _{1 ,j =1} ) на множестве (A) сконцентрировано в O( n ^{( a} - ¹⁾ / ² ) окрестности (почему именно в такой окрестности, будет показано ниже) наиболее вероятного значения:

xij ^ LiWj/N — na-1,  i, j = 1, ..., n, (2)

которое ищется с помощью метода множителей Лагранжа [2, 51]. Формулу (2) можно интерпретировать как наличие у районов «потенциалов притяжения» [2]:

Такой способ расчета матрицы корреспонденций в литературе часто называют гравитационной моделью:

xij AiBj Li^Vj exp( Ytij) , где {Ai}П=1 и {Bj}n=1 определяются из соотношений [2, 30, 32]:

Li/VN — exp(XL), i = 1, ..., n

Ai =

- 1

n

Е BjWj exP(-Ytij) I j=1

Bj = (l2

i =1

AL exp(—Ytij)

)

- 1

и

W j /VN — exp( X W ) , j = 1 ,...,n, произведение которых даёт пассажиропоток x _i ^∗ _j , i, j = 1 , ..., n (асимптотически совпадающий с математическим ожиданием и медианой).

Исследуем теперь, следуя [1, 2, 30], явление концентрации стационарного распределения Р ( {x ij } п =1 j =₁ ) в окрестности наиболее вероятного значения {x j } ' ='1_{; /} =₁ . Для этого прежде всего заметим, что из определения {x j } П =1 j =₁ (см. также сноску 12) следует

Описанная модель (точнее говоря, рассчитанная по этой модели матрица корреспонденций) активно используется в теоретико-игровых моделях (например, базирующихся на принципах Дж.Г. Вар-дропа) равновесного распределения потоков [32] (см. также главу 1 в пособии [54]). Подробнее об этих моделях речь пойдет в статьях Е.А. Нурмин-ского и Н.Б. Шамрай, В.И. Швецова, Е.В. Гасни-ковой и Ю.В. Дорна из этого же сборника. Один из возможных способов определения времени в пути, в зависимости от загрузки ребра, предложен в статье М.Л. Бланка. Иной подход к выводу гравитационной модели имеется в статье П.П. Бобрика. Заметим также, что задача (1) по своим свойствам очень похожа на транспортную задачу (см. статью А.В. Колесникова).

V{x ij } n = ⁿ1,j =1 € ( A ) -

n n

Е

д ln p ( {x ij } n = ⁿ 1 , j =

∂x ij

— х

х (xij — x*j) < 0.

Поэтому

V{xjj }n=n1 ,j=1 € (A)  3 9 € [0,1]:

ln Р({xij }'=.,j=1) < ln p({xij }'Г.,j=1)+

n,n

+ Е i=1,j=1

Но

д2 ln p({xj 9 + xij • (1 — 9) }'=1 ,j=1) dx2j                X

⁽ x ij ^{— x} j ^{) 2}

дц (ln p({xij }n," ,j = 1)) =

систему ограничений (в методе предполагается, что есть ограничения только в виде равенств), и разрешение полученной системы (размерность которой как раз равна числу двойственных переменных) относительно двойственных переменных. Для рассматриваемого далее частного случая V i, j = 1 , ..., n ^ t ij = т >  0 все это можно сделать аналитически и в результате получить формулу (2). Отметим здесь также эффективность сепарабельных (функционал декомпозируется в аддитивную сумму функций одного аргумента) алгоритмов типа Нестерова–Немировского для задач энтропийного программирования, возникающих при нахождении равновесий макросистем [53].

• ¹³    Отметим, что хотя в этом случае динамика рассматриваемой нами макросистемы обратима по времени (так же, как и в примере 1), макросистема (в каком бы состоянии она не находилась в нулевой момент времени) по прошествии достаточно большого времени окажется в малой окрестности равновесного макросостояния (характеризующегося наибольшим из возможных значением энтропии) и будет в дальнейшем пребывать в этой окрестности подавляющую часть времени. Схожая ситуация имеет место и в статистической физике (см., например, [8, 11, 14, 18, 19, 27]).

  д ^{2 дх} 2

  
  
  
  

  n,n

  Е х

  г =1 ,3 =1

  
  
  
  
  

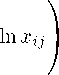
  x ij

  
  

  Следовательно, приходим к «неравенству о концентрации меры»:

  
  

  V M >  0 , V {х гз ^,3 =1 Е ( A ) :

  
  

  n,n

  Е

  г =1 ,з =1

  
  

  ⁽ x ij - x j ^{) 2}

  2 max {х гз ,х Е }

  
  

  > M —

  
  

  - Р ( {х гз } " =1 ,3 =1 ) <  e ^{- M} p (. } - = ,3 =1 ) .

  
  

  Из этого неравенства имеем результат о концентрации распределения p ( {x ij } ” =’1 3 =1 ) на множестве (A) в O( n ⁽ “ - 1) 1 ² ) окрестности наиболее вероятного значения {x - } ” =’1 3 =1 :

  
  

  3 A >  0 : lim P ( V i, j = 1 , ..., n — 1x 3 ( t ) /x * ₃ — 1 | <  t ^^

  
  

  < A/n ⁽ “ - 1) 1 ² ) > 0 , 999 .

  
  

  методов исследования концентрации меры упомянем теоремы тауберова типа [61] и мартингаль-ные неравенства [60]. Ввиду всего вышесказанного важно отметить, что поиск наиболее вероятного распределения — это особенность работ, в которых изучаются равновесия макросистем. Но также важно заметить, что наиболее вероятное распределение в содержательных задачах асимптотически (по размеру системы) эквивалентно математическому ожиданию (в работе [2] соответствующие выкладки проделаны на примере модели расчета матрицы корреспонденций А.Дж. Вильсона, см. также следующий пункт) и медиане [59].

  Замечание (модели Д. Бернулли–Лапласа, П. и Т. Эренфестов). Важно обратить внимание на то, что описанный способ изучения равновесных состояний макросистем применим к достаточно широкому классу макросистем (модель Д. Бернулли–Лапласа, модель Эренфестов, круговая модель М. Каца и др. (см., например, [8, 27, 62] и цитированную там литературу)), в том числе встречающихся в экономике, биологии, социальной сфере [3, 4; 15–24].

  
  

Замечание (о других возможных подходах к исследованию концентрации стационарного распределения). Один из способов восходит к методу вычисления математических ожиданий Дарвина–Фаулера [2, 5, 9] (метод производящих функций и анализ их асимптотического поведения методом перевала) — в этом случае концентрация наблюдается в окрестности математического ожидания (интересные приложения этого метода в комбинаторике имеются, например, в [55], см. также статью А.А. Замятина и В.А. Малышева в этом сборнике и конец следующего пункта). Исследование концентрации в окрестности математического ожидания можно также приводить, например, используя предельные меры [56], метод канонических ансамблей [57] или обобщённую схему размещения [58], нашедшие применения к задачам асимптотической перечислительной комбинаторики, ¹⁴ к исследованию случайных матриц и уравнений, к изучению статистических свойств группы перестановок с приложениями к теории разбиений (диаграммам Юнга) и асимптотической теории чисел, а также к теории предельных форм. К методу производящих функций также тесно примыкают метод моментов [58], метод пуассоновской и гауссовской аппроксимации (метод локальной предельной теоремы) [7, 58]. Другой способ восходит к принципу концентрации А. Пуанкаре и П. Леви, получившему дальнейшее развитие в работах В.Д. Мильмана и др. [59] — в этом случае концентрация наблюдается в окрестности медианы. ¹⁵ В заключение краткого обзора

III. Общая схема исследования равновесий макросистем

Ниже приводится (во многом под влиянием работ [18, 19]) общая схема, в которую «ложатся» примеры 1 и 2.

Предположим, что некоторая макросистема может находиться в различных состояниях, характеризуемых вектором n с неотрицательными целочисленными компонентами (скажем, в модели «кинетика социального неравенства» n _г ( t ) — количество жителей города, имеющих в момент времени t ^ 0 i рублей). Будем считать, что в системе происходят случайные превращения (химические реакции). Пусть n - n — а + в , ( а,в ) Е J — все возможные типы реакций, при этом ( а,Р ) Е J ^ ( Р,а ) Е J . Введем, следуя Березину-Клесову (1978) [19], интенсивность реакции:

A (a, в)(n) = A (a, в)(n — n — а + в) =

= м1 -Piaiка(мм\ Д щ • ... • (n — аг + 1), A г:ai >0

где Ka ^ 0 — константы реакции (в химической кинетике — постоянные, а в социодинамике (В. Вайдлих, 2000 [20]) — необязательно); при этом часто считают 52г nг = M, т. е. A(a в) (n) — вероятность осуществления в единицу времени перехода n — ri—а+(3: в единицу времени равновероятно выбираются («приближение среднего поля») любые два жителя города и в зависимости от того, в каких состояниях они находились, «случайно» переводятся (разыгрывают один рубль) в новые состояния. На макроуровне все это соответствует принципам химической кинетики (закон действующих масс Гульдберга–Вааге, 1864 [18]).

Предположим теперь, что множество J не зависит от M , и в начальный момент времени для любого i существует предел ci (0) = lim ni (0)/M. m —^

Тогда (Малышев–Пирогов–Рыбко, 2004 [19, 63]) в произвольный момент времени t >  0 и для любого i существует предел по вероятности (заметим, что n _г ( t ) — случайные величины, тем не менее c i ( t ) — уже не случайные величины):

c i ( t ) п = ' lim n i ( t ) /M.

M —-^

Описанный выше приём называется каноническим скейлингом. В результате такого скейлинга приходим к «динамике квазисредних» (терминология В. Вайдлиха [20]):

d^ = £ ( в _г - а _г ) K f ( c ) П c ? . (3) ( a,в ) e j j

Эти же уравнения можно получить и по-другому. А именно, как приближенную динамику средних c _г ( t ) = E [ n _г ( t ) /M ]. Приближенную в том смысле, что при выводе (1) используется приближение

F (c _г ( t )) « E [ F ( n ( t ) /M )]

Несложно проверить, что ξ , удовлетворяющее (4), является неподвижной точкой системы (3). Более того, если существует хотя бы одно положительное решение системы (4), то тогда все неподвижные точки системы (3) удовлетворяют условию (4), также называемому условием унитарности, или условием Штюкельберга–Батищевой–Пирого-ва. Покажем, во многом следуя В.В. Веденяпину [18], что в этом случае (существования хотя бы одного положительного решения (4)) траектория (3) сходится к неподвижной точке (какой именно, зависит, вообще говоря, от «точки старта»). ¹⁷ Для этого, следуя второму методу Ляпунова, введём (минус) энтропию:

H = E c • ^(ln( c i /С г ) ^- 1)

г

и покажем, что она является функцией Ляпунова для системы (3). Посчитаем полную производную H в силу системы (3):

^d H = £ к а п j y a x

( a,p ) e j

X 6» ^П У? ^- * *

j

£ ( Э г ^{- а} г )^ +

+ £ K | W в г - а г ) =

( a,p ) e j       j               ^г

= £ K a п j y ? • l»п <■—"■ , ( a,в ) e j       ^{j                  г}

для «достаточно хороших» функций F (например, полиномов).

Это верно в случае пикообразного распределения n _г ( t ). ¹⁶ Пусть существует хотя бы одно положительное решение ξ ^{^} системы (условие динамического равновесия, В.В. Веденяпин (2001) [18], Малышев–Пирогов–Рыбко (2004) [19, 63], Бати-щева–Веденяпин [64]):

где введено обозначение у _г = c _г /t _г . Заметим, что

^£ К П ^п 3 - a ₌ ^£ _к з ^{п e} - a ₌

Z—i ^{3 e} j y j Z—i a ^e j y j

( a,3 ) E J       ^j               ( a,3 ) E J       ^j

£ K m t ? = £ ^к ж в ) ^- ,  (4)

3 :( a, 3 ) E J ^j          3 :( a,3 ) E J ^j

= E кЩ j y j ¹.

( 3,³ ) E J       ^j

Таким образом,

T = - £ K 3 П t " - y ? x ( 3,³ ) E J       ^j

где К З (c) = K 3 , а а — произвольный, но такой, что 3 в : ( а,в ) G J .

Частным, но часто встречающимся в приложениях, случаем условия (4) является условие детального равновесия:

x I П у ? ’ - j inn y a * ^{- :}’* - П y ? - ¹ +1) <0 , j                    г                 j

K m j

j

= к в П t j j . j

поскольку u in u - u +1 > 0 при u >  0, и равенство достигается в одной точке u = 1.

Оказывается (Малышев–Пирогов–Рыбко [19, 63]), что условие (4) можно проинтерпретировать

как условие инвариантности пуассоновской меры [50]: ¹⁸

Ц (" ) = П Xn■/с*!,

i где Xi = Е* M, а С* — произвольное решение (4); относительно предложенной стохастической марковской динамики. Эта мера экспоненциально быстро концентрируется, с ростом с*, в окрестности наиболее вероятного состояния (также удовлетворяющего условию (4)), которое и принимается за положение равновесия макросистемы. Задача поиска наиболее вероятного макросостояния асимптотически эквивалентна задаче максимизации энтропийного функционала (воспользовались n! = V2nn(n/e)n(1 + o(1)) — формулой Стирлинга):

Тогда по формуле Коши:

E["p 1 •... • "pQ] = z(2^ fdzi •... •dZmx

< {П Fk-^П fe^) p'F(СА)}

Z .■  f ^ '-‘m {П =-"*-‘}

F (с; A)

E «-Y, " • (M "i/Xi) - 1) = -M • H i

Здесь математическое ожидание E [ " P1 ■ ...■ n p Q ] считается по вероятностной мере, порожденной мерой Пуассона ц ( С ), а интегралы по dz * берутся в комплексной плоскости по замкнутым контурам, охватывающим точку ноль. Используя метод перевала [67], асимптотически оценим математическое ожидание:

на множестве, заданном (как правило, линейными) ограничениями — законами сохранения (интегралами движения для (3)).

Действительно, будем считать, что ограничения (законы сохранения) задаются СЛАУ АС = d , где А = ||A fc; | | — матрица максимального ранга ( к = 1 , ..., т ). Обозначим через A множество неотрицательных целочисленных векторов "  , удовлетворяющих АС = d . Тогда равновесие С * находится как решение задачи E ( С ) ^ max n _e а (поскольку функционал строго вогнутый и считаем n * ^ 1, то целочисленностью переменных можно пренебречь). Используя принцип Лагранжа, можно показать, что решение этой задачи представляется в виде

E [ "pI •--.-"PQ ]« F;^ ('" 1 *) -P' p' x

x I1? (зас;) F(С; А>} ■ где «точка перевала» С* определяется как решение системы:

z* • (dF(С; А)/dz*) « d* ■ F(С; А), к = 1, ..., т.

В частности, ¹⁹

E[с*] « Xi П(z*)Aki,  D["i] « Xi П(z*)Aki, kk

где z определяется как решение системы уравнений:

Ci(с*) = Xi exp

(? А ** » *)

£ a*'Jx* п =A-j. = d*,

к = 1, ..., m.

где двойственные переменные (множители Лагранжа) С определяются из системы уравнений АС ( С ) = d .

Приведем, во многом следуя [2], другой путь (восходящий к Дарвину–Фаулеру), по которому можно прийти к аналогичным формулам.

Для этого введем производящую функцию:

Очевидна связь «точки перевала» С с двойственными переменными С ^: z * = exp( y * ).

IV. Заключение

F(С; А) = ^ц(С) H^Fl Aklnl n >o       *

= П£ ^(X' ⁿ *^ i n i ^ 0

e ^{X i}

=П - (Ч(П ’^-)- ОУ

В статье обсуждается концепция равновесия макросистемы. Приводятся различные подходы к обоснованию следующего принципа: равновесие = наиболее вероятное макросостояние инвариантной (стационарной) меры динамической системы (марковского процесса), порождающей исследуемую макросистему. Рассматриваются примеры конкретных макросистем. В частности, один из примеров «объясняет» популярную в приложениях модель А.Дж. Вильсона расчета матрицы корреспонденций.

Повторим в заключение описанную в статье схему.

• 1.    Макросистема состоит из огромного числа пронумерованных агентов, каждый из которых может находиться в одном из возможных состояний. Число состояний, как минимум, на несколько порядков меньше числа агентов (иногда можно и без этого требования). Распределение агентов (с учетом их номеров) по состояниям будем называть микросостоянием, а без учета номеров — макросостоянием.

• 2.    Задана марковская динамика распределения агентов по состояниям, в основу которой на микроуровне положена равноправность агентов одного типа (в приближении среднего поля) и заранее прописанные возможности случайных превращений (переходов) агентов (химические реакции): равновероятно выбирается агент и в зависимости от того, в каком состоянии он находится, «случайно» переводится в новое состояние. Аналогично рассматриваются парные взаимодействия и взаимодействия, в которых участвует большее число агентов. На макроуровне это соответствует принципам химической кинетики (Гульдберг–Вааг, 1864).

Предполагается, что из любого возможного макросостояния можно перейти согласно такой динамике в любое другое (характерное время такого перехода определяет скорость сходимости к равновесию). Также считается, что описанная динамика имеет макрозаконы сохранения. Соотношения (как правило, линейные) между макровеличинами, которые не меняются со временем.

Пусть выполняется условие: динамика задана линейной полугруппой (однородность), динамика «обратима» (детальный баланс, условие динамического равновесия).

Тогда эргодическая марковская динамика приводит на больших временах к стационарной (инвариантной) пуассоновской (сложной) мере (прямое произведение распределений Пуассона) на пространстве макросостояний. Эта мера экспоненциально быстро концентрируется, с ростом числа агентов, в окрестности наиболее вероятного макросостояния, которое и принимается за положение равновесия макросистемы. Задача поиска наиболее вероятного макросостояния асимптотически (по числу агентов) эквивалентна задаче максимизации энтропийного функционала (воспользовались формулой Стирлинга) на множестве (как правило, аффинной структуры), заданном ограничениями — законами сохранения. Этот же энтропийный функционал (взятый со знаком минус) возникает как функция Ляпунова динамики, полученной в результате канонического скейлинга исходной марковской динамики. Отыскание предельной неподвижной точки (этой динамики), в которую придет система, сводится к решению той же самой задачи энтропийно линейного программирования. Приятной особенностью такого класса задач является явная (легко выписываемая) зависимость решения прямой задачи через двой- ственные переменные. Поскольку число ограничений, как правило, на много порядков меньше числа прямых переменных, то эффективные численные методы базируются на решении двойственной задачи: задачи минимизации выпуклой функции.

Работа поддержана грантами РФФИ № 08-01-00959-а, 08-07-00501-а, 08-07-00158-а, 10-01-00321-а, 10-07-00620-а, 11-01-00494-а, РГНФ № 08-02-00347, ПФИ ОМН РАН № 3, ПФИ Президиум РАН П-2. Работа проведена в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009--2013 годы (мероприятие 1.2.1, НК-15П, П949; мероприятие 1.3.1, НК-215П, П1490).

Настоящая статья представляет собой запись нескольких лекций, прочитанных первым автором студентам МФТИ в весеннем семестре 2009 / 2010 учебного года в рамках курса по выбору «Математическое моделирование транспортных потоков».