О возможности детектирования реликтовых гравитационных волн в различных моделях космологической инфляции со скаляром Гаусса-Бонне

Инфляционная гипотеза, формирования наблюдаемой Вселенной в настоящий момент является наиболее общепризнанной. Первые инфляционные модели были сконструированы на. основе ОТО и некого скалярного (инфлатонного) поля, квантовые флуктуации которого привели к образованию видимой структуры Вселенной. В дальнейшем рассматривались модифицированные теории гравитации, включающие члены кривизны высших порядков. Указанные члены трактуются как низкоэнергетические поправки к струпной теории или модели супергравитации, среди которых можно отметить скаляр Гаусса. - Боппе, появляющийся при рассмотрении поправок в теории гетеротических струп или же гравитации Лавлока, (обзор па. различные модели на. основе ЭГБ

• ¹    E-mail: gevorgbek.manucharyan@gmail.com

гравитации представлен, например, в работе [1]). Скаляр Гаусса. - Боппе влияет па. космологическую динамику в четырехмерном пространстве при неминимальной связи со скалярным полем, что в свою очередь приводит к изменению характеристик космологических возмущений, в том числе скорости распространения реликтовых гравитационных воли. Последние являются особым предметом интереса, после удачного детектирования гравитационных воли от слияния двойной системы детекторами коллаборации LIGO. Целью настоящей работы является обсуждение особого вида, временной эволюции иифлатоииого поля в гравитациях Эйнштейна, и Эйнштейна. - Гаусса. -Боппе со слабой связью скалярного поля и скаляра. Гаусса. - Боппе, верификация данной модели по наблюдательным ограничениям, оценка, частоты обрезания реликтовых гравитационных воли, а. также оценка, возможности детектирования данных воли на. гравитационно - волновых детекторах LIGO, LISA, DECIGO.

• 1.    Рассматриваемые модели

В рамках ОТО с действием Эйнштейна. - Гильберта.

S =

I d⁴ xV-g [2 R

— g^ 2 ЭцФЭу Ф —

v (Ф)].

(i.i)

уравнения космологической динамики записываются в виде [2]

V (Ф) = 3Н ² + Н ,

(1.2)

Ф ²

-2Н,

(1.3)

где V(Ф) - потенциал скаляриого поля Ф, Н = ^ - параметр Хаббла.

В качестве решения уравнений (1.2)-(1.3) предлагается рассматривать оригинальное решение, полученное путем выбора, формы эволюции скалярного поля исходя из необходимости появления стадии повторного ускоренного расширения на. больших временах,

Фе (t) = —2т

(t - у ту

^{е bt + Ф}0,

(1.4)

где Фо - значение скалярного поля в начале инфляции, т, b - константы, с параметром Хаббла

Н (t) =

e-2btA(t)

+ ⁺

2b² + 2bm + т² 2b

(1.5)

где

A(t) = 2b²(mt — 1)² — 2bт(тt — 1) + т².

Форма, зависимости потенциала, от скалярного поля задается соотношением:

^ve ^(Ф) =

4b2

/ 4b⁴ у² W (ру)

2b⁴ у² W (ру)²

+ 2b⁴ у² —

( ^{ь 2} у ^{2 (2W} (ру) ⁺ 1)   ¹ 2 ( 2                  ^

"Ц —4W (ру)2--26 (у - 4)+26т + т)

(1.6)

где р = ^be ₂ ^ , у = Ф — Ф_о, W - w-функция Ламберта.

Учет неминимального взаимодействия скалярного поля и скаляра Гаусса - Бонне Rqв = R² — 4R_pyR^pv + R^upaR^^³¹⁷ позволяет записать действие в виде:

Sc в =

2 д¹" ЭрФсвЭ^Фс в — Vc в (Фс; в)

2^^(Фо b^)rgb ,

(1.7)

• а. уравнения фоновой динамики (1.2)-(1.3) в виде (1.8)-(1.9), которые представляют собой уравнения космологической динамики для случая гравитации Эйнштейна. - Гаусса. - Боппе:

Vgв(Фсв) = 3Я2_В + Я_Ов - 10Я3_В ф - 2Я2_Вф - 4H_gbH_g вФ             (1.8)

2 ф 2_В = -Я_о в- 2Я3_В ф + 4Яе_ВЯе _BUHH 2_В ф                (1.9)

где ф - функция неминимального взаимодействия скалярного поля и скаляра Гаусса - Бонне [1].

В качестве наблюдательных ограничений для моделей, являющихся решением уравнений (1.2)-(1.3) или (1.8)-(1.9) рассматриваются спектр мощности скалярных возмущений Рд — 2.1 х 10^-9, спектральный индекс скалярных возмущений пд = 0.965±0.004 [3], тензорно - скалярное отношение т <  0.032 [4], а также динамические характеристики Вселенной, а именно: число е-фолдов и наличие эпох инфляции и повторного ускоренного расширения.

Стоит отметить, что учет взаимодействия скалярного поля и скаляра. Гаусса. - Боппе (при слабой неминимальной связи) путем добавления константы неминимальной связи gqb позволяет верифицировать в рамках гравитации Эйнштейна. - Гаусса. - Боппе (ЭГБ) ряд моделей, не прошедших верификацию в рамках ОТО.

Уравнения космологической динамики для моделей со слабой связью скалярного поля и скаляра. Гаусса. - Боппе рассматриваются в виде [1] (1.10)-(1.12), которые являются приближенными решениями уравнений (1.8) - (1.9) (приближение основано на. слабой связи скалярного поля и скаляра. Гаусса. - Боппе, а. также приближении медленного скатывания)

Vg в(Фс в) = 3Я2 + (1 + gq в)Яе,(1-Ю)

^ф2В. = ^{-2(1 - g}G В^)ЯЕ,Д-И)

причем в случае минимальной связи (асв = 0) уравнения (1.10)-(1.11) сводятся к виду (1.2)-(1.3).

Отметим, что для модели (1.4) функция неминимальной связи имеет вид:

A

ДфС В) =  -------------------------------------------------—-2

(-m² (2W (p^gв) (W (р^с, в) + 1) + 1) • exp (2W (рр_с, _в) - —) + 2b² + 2bm + т²) (1-13)

• ^Г^^С ^ В = Т1-Ц ^-ф0

В терминах ЭГБ гравитации представленная форма, параметра. Хаббла. (1.5) можно переписать с учетом (1.10)-(1.11) в виде

^ЯС в = ^яе ^{(1 + G}GB^eE ),                                  11-14)

• а. потенциал скалярного поля записывается как:

Vgв = Ve - асвЯ_Е,                                  (1-15)

Для проверки соответствия модели наблюдательным ограничениям рассматривается следующая связь между характеристиками реликтовых возмущений для случаев гравитации Эйнштейна. - Гаусса. - Боппе и ОТО:

• ⁿS(GB) ^{- 1} = ^{- 4е}Е ^{+ 25}Е = ^пЕ(_Е) ^- 1,                            (1-16)

• 2. Реликтовые гравитационные волны и возможность их регистрирования

TGВ = 16(1 - ас вДе = Т_Е,                             Д-Гц)

где е и 5 - первый и второй параметры медленного скатывания. Наблюдательные ограничения для модели в свою очередь накладывают ограничения на. возможные значения константы пемипималыюй связи асв-

Стоит отметить, что стандартные космологические модели подразумевают непосредственный переход от стадии инфляции с параметром состояния ио ь 1 к стадии преобладания излучения ио = 1/3. Однако, учет неминимальной связи скалярного поля и скаляра Гаусса - Бонне дает теоретические основания для существования промежуточной стадии преобладания «жесткой энергии» с параметром состояния 3 <  оо < 1, что оказывает существенное влияние на характеристики реликтовых гравитационных волн [5].

С учетом связи (1.14) можно сказать, что для рассматриваемой модели тензорно - скалярное отношение не зависит от констант модели. Таким образом установлено, что рассматриваемая модель верифицируема в рамках ЭГБ гравитации по величине тензорно - скалярного отношения, а также наложены ограничения на константу неминимальной связи, а именно ctQ^^] Е [—0.5, 0].

Плотность энергии реликтовых гравитационных волн можно оценить [6] безразмерной вели чиной

Q_gw(/ ) ~ ^Gw(f ) •

f 1 ,/ ,

11.27 • (Г ,^/>/rd ,

(2.1)

где HGw =

— 9 ( ^3w-i ^

2  3w+1

10 ¹⁵r/h2. h ~ 0.69 - относительная постоянная Хаббла., параметр a_s

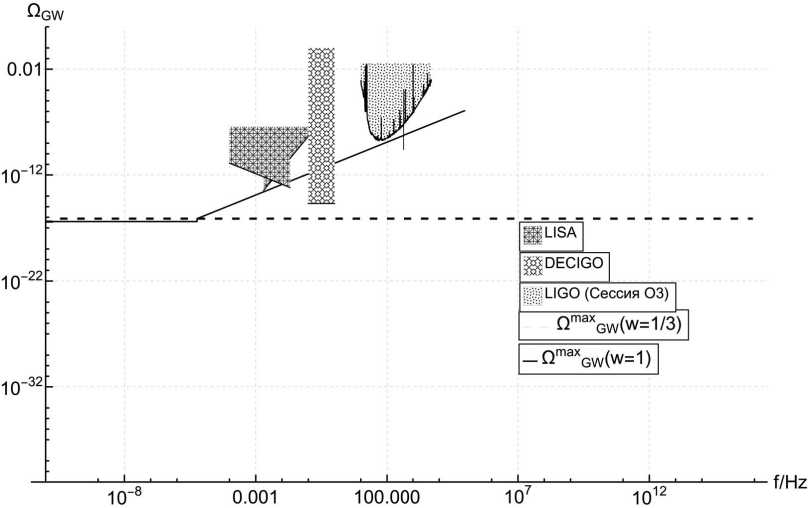
Рис. 1. Плотность энергии реликтовых гравитационных волн для предельных значений параметра состояния и чувствительность гравитационно - волновых антенн LISA [7], DECIGO [8] и LIGO [9].

/rd - это частота моды, которая соответствует размеру горизонта в начале эпохи преобладания излучения, в настоящей эпохе. Также можно оценить частоту обрезания спектра реликтового гравитационно - волнового фона с учетом интегрального условия на плотность энергии

Гfcutoff fbbn

H gw (f ) / < 1.3 X 10^-6,

(2.2)

где /ььп ~ 1.8 x 10 ¹¹ Гц.

Для рассматриваемой модели соотношения (2.1) и (2.2) позволяют установить максимальную плотность энергии О™^ ~ 1.16 X 10-6 на частоте обрезания fcutoff ~ 91.7кГц, а также определить, что величина плотности энергии реликтовых гравитационных волн недостаточно велика для детектирования на установках LIGO, однако попадает в полосу детектирования антенн LISA и DECIGO (рис. 1)

Заключение

Таким образом, в данной работе рассмотрено решение уравнений космологической динамики в рамках гравитации Эйнштейна. - Гаусса. - Боппе и ОТО, установлена, верифицируемость рассматриваемой модели по величине тензорно - скалярного отношения с учетом экспериментальных результатов, получены ограничения на. константу неминимальной связи скалярного поля и скаляра. Гаусса. - Боппе, получена, частота, обрезания спектра, реликтовых гравитационных воли, которая приблизительно равна. 91.7кГц, а. также оценена, теоретическая плотность энергии реликтовых гравитационных воли для рассматриваемых моделей, с максимальным значением fig^ ~ 1.16 х 10-6. Установлено, что их нельзя регистрировать на. гравитационной антенне LIGO, однако они попадают в теоретическую полосу детектирования установок DECIGO и LISA.