О возможности использования индекса Винера для вычисления признаков текстов на естественном языке

DOI:

Доктор физико-математических наук, заведующий кафедрой компьютерных наук и экспериментальной математики, Волгоградский государственный университет ,

,

1.    Индекс Винера

Пусть G = (V, Е) - связный граф с множеством вершин V и множеством ребер Е . Обозначим через N = | V | число вершин графа. Предположим, что каждому ребру е Е Е приписан некоторый неотрицательный вес w(e) . Если y — некоторый путь в графе G , то его длина |у| равна сумме весов ребер, из которых этот путь состоит. Обозначим через

IpqIg = inf |y| γ минимальную длину путей, соединяющих вершины p,q eV . Тогда индекс Винера W (G) [16] определяется по формуле

W(G) = 2 Е | р« | с .

p,4 ^ v

Наряду с индексом Кирхгофа, индекс Винера используется для вычисления сложности графа [3]. Если граф G представляет собой простую цепь G = P _n и все веса равны 1, то

W(G) = W(P _N ) = С ^ +1 = ^{( N +1)} N ^{( N} - 1) . ⁺             6

Если граф G представляет собой дерево в виде «звезды» S _N , то есть когда ребра соединяют все вершины графа с некоторой одной выделенной, то

W (G) = W ( S n ) = (N - 1) 2 .

Для полного графа G = KN очевидно w (G) = w (Kn ) = cN = N (N— 1).

Наряду с величиной W(G) будем рассматривать приведенный индекс Винера

^{W ( G ) W}" ^{( G )}    (N - 1) 2 .

Известно [14], что для единичных весов и произвольного дерева Т с N вершинами имеет место неравенство

W ( S n ) <  W (Т ) <  W ( P n ),                         (1)

а для произвольного связного графа с единичными весами – неравенство

W ( K n ) <  W(G) <  W ( P n ).

Нормирующий множитель для W _n выбран исходя из того, что W _n (T ) >  1 для дерева Т с единичными весами ребер, причем равенство достигается только если это дерево представляет собой «звезду» S _n . Так что нормированная величина W _n меряет отклонение дерева от графа вида S _n . Одной из задач, связанных с введенной величиной, является задача вычисления остовного дерева Т графа G с минимальным индексом Винера. Пусть S(G) - множество всех остовных деревьев графа G . Тогда в этой задаче требуется найти Т * Е S(G)

^Т * = argmin _{T e S ( G )} ^{W ( Т} ).                             (2)

Заметим, что эта задача на минимум может иметь не единственное решение. В таком случае предполагается найти хотя бы одно остовное дерево, минимизирующее W(Т ) . В работах [6; 11] доказана NP-полнота этой и подобной задачи для поиска подграфа минимального индекса Винера. Отметим, что в работе [11] задача поиска дерева с минимальным индексом Винера решена для евклидовых деревьев конечного множества точек в выпуклом положении, то есть для вершин выпуклого многоугольника на плоскости. Для евклидовых пространств задача ставится с весами, равными евклидовым расстояниям между вершинами для полного графа. В частности, в [11] доказано, что евклидово дерево с минимальным индексом Винера планарно, то есть ребра дерева попарно не пересекаются.

Пусть G = (V,E ) - связный граф, вершинами которого являются точки евклидова пространства R ” ,n > 1 . В качестве весов ребер выбираем расстояние между соответствующими вершинами ребра графа. Определим величину

Е \ pq \ G

WPG) =        , p,pEV где \pq\ = |р — q\ обозначено расстояние между точками p,q eV С R”. Величина We(G) характеризует извилистость кратчайших путей в графе G и всегда We(G) > 1.

Поиск экстремалей для индекса Винера – одна из сложных задач теории графов. Отметим недавнюю работу [15], в которой решается задача поиска графа с минимальным индексом Винера в классе графов Халина [12]. В работе [8] рассматривается задача минимизации произведения W(G) • Н (G) , где

Н= Е s — p,qev,p=q \pq\G так называемый индекс Харари. Там доказано неравенство

W(G) • Н(G) > - ([(N — 1)N — M][(N — 1)N + 2M]), где M - число ребер в графе. При этом равенство имеет место тогда и только тогда, когда диаметр графа G не превосходит 2.

Основная цель настоящей работы состоит в том, чтобы показать возможность использования индекса Винера и его модификаций для вычисления признаков текстов на естественном языке. Мы выделяем четыре таких признака и применяем их для решения задачи определения информативности текста. Поясним последний термин подробнее. В последнее время в медийном пространстве увеличивается количество текстов, обладающих признаками недостоверного содержания и служащих средством манипуляции общественным сознанием. Деструктивные тексты разнообразны, имеют различную природу, часто характеризуются пересекающимися признаками и с трудом поддаются классификации. К медийным текстам, образующим деструктивные медийные практики, исследователи относят инфодемические сообщения, фейковые тексты и тексты, использующие техники «кликбейтинга» [2]. Разновидностью недостоверных медийных сообщений являются тексты, созданные с целью привлечения внимания читателя и увеличения количества переходов на сайт. Эти тексты строятся по модели информационного сообщения, но их содержание не соответствует заявленному в заголовке тезису (то есть используется технология «кликбейтинга»). Таким образом, текстовые сообщения не соответствующие основной цели медийного дискурса – информированию, являются достаточно разнородными, не имеют четко выраженных критериев выделения, имитируют достоверные сообщения, используя определенную структуру и языковые средства. Кроме того, приемы создания таких текстов постоянно модифицируются, отражая новые практики создания деструктивного контента. Соответственно, важной задачей исследователей является составление параметрических моделей деструктивных текстов, что позволит в дальнейшем решить задачу поиска и идентификации деструктивной информации в разножанровых текстах автоматизированным путем.

Цель нашего исследования – построение обученной модели естественного языка медийных сообщений и анализ точности автоматического распознавания информативных и недостоверных медийных сообщений на ее основе. Существуют различные подходы к автоматическому определению текстов, содержащих признаки дезинформации. В работе [4] авторы отмечают, что статистическая обработка множества поддельных статей позволяет выделить наборы ключевых слов, которые с определенной долей вероятности сигнализируют о возможности, что статья является поддельной. Автоматическое определение «кликбейтинга» на материале английского языка проведено в работах [7; 9; 13]. В них предложена гибридная техника категоризации кликбейтных и некликбейтных статей путем интеграции различных функций, структуры предложений и кластеризации, после чего к набору данных применяются модели машинного обучения, чтобы с помощью соответствующих метрик получить оценки точности распознавания деструктивного текста.

2.    Графовая модель текста

Здесь мы вкратце опишем графовую модель текста [1], используемую нами в дальнейшем для вычисления признака текста на основе индекса Винера. Мы предполагаем, что текст написан с использованием конечного алфавита X и представляет собой конечную последовательность U символов алфавита X. Текст U разбивается на отдельные слова и предложения посредством множества разделителей D С X. Пусть V - это список уникальных слов текста - словарь. Построим для пары u,v Е V ребро е, если в тексте найдется предложение, включающее в себя эти два слова. В результате получим граф Gu = (V, Е) заданного текста. Надо заметить, что этот граф не обязательно связен. Можно даже сказать, что этот граф, скорее всего, для реальных текстов будет несвязным. Это обстоятельство можно объяснить одним из статистических законов Ципфа - в множестве V подавляющее число слов, которые в тексте встречаются один раз. В указанной выше работе [1] были найдены характеристики графа текста, которые чувствительны к перемешиванию слов текста. При перемешивании текста теряется его осмысленность, хотя статистически он тот же – частоты слов текста не изменяются. Одной из таких характеристик графа текста является медианное значение степеней вершин графа. Другими словами, если di < d2 < ... < dN - степенная последовательность графа Gu, то медианное значение равно d[N/2]. Надо сказать, что по аналогии для заданного текста можно построить и другие графы. Например, если в качестве предложений использовать n-граммы, тогда граф будет отражать свойства следования слов друг за другом в тексте. Этот подход исследовался в работе [5] для определения естественного происхождения текста.

Пусть для заданного текста U построен граф G u = (V, Е ) . Припишем каждому ребру е Е Е графа вес w(e) = 1 . Как было указано выше, граф G может быть несвязным. Индекс Винера вычисляется для связного графа. Поэтому мы будем строить по графу G новый связный граф, добавляя с этой целью новые ребра к множеству Е . Это можно сделать различными способами. В нашем исследовании использовался простой метод добавления k — 1 новых ребра, соединяющих последовательно случайно выбранных k слов по одному из каждой компоненты графа G u . При этом веса добавленных ребер выбираются равными 1. По построенному графу мы будем вычислять индекс Винера специально сконструированного остовного дерева Т Е S(G u ) . Это дерево будет приближенным решением вариационной задачи (2). Алгоритм построения этого решения будет описан ниже.

3.    Алгоритм приближенного вычисления остовного дерева с минимальным индексом Винера

Для приближенного решения задачи (2) мы совместим два случая. Первый случай - построение приближенного решения для конечного набора точек V евклидова пространства R ” ,n > 1 и второй случай - для взвешенного графа. Совмещение производим за счет того, что в первом случае в качестве графа берется взвешенный полный граф с весами ребер, равными их длинам в евклидовом пространстве. Нам понадобится следующая простая формула для индекса Винера произвольного дерева. Пусть Т -произвольное N -вершинное дерево с неотрицательными весами ребер w(e) >  0, е Е Е . Для ребра е = (а,Ь) Е Е введем обозначения Т _а ,Т _ъ для деревьев, получаемых из дерева Т удалением ребра е , причем а Е Т_а , b Е Т ъ . Пусть N _a , N - это число вершин в этих деревьях. Ясно, что N _a + N _ъ = N . Нетрудно заметить, что

W (Т )= £ w(e)N a Nъ. (3) е=(а,Ь) Е Е

Эта формула является основой для получения оценок (1). Получается эта формула из определения индекса Винера посредством изменения порядка суммирования длин ребер – вместо суммирования по всем парам вершин необходимо перейти к сумме по всем ребрам и подсчитать, что число путей, проходящих через ребро е = (а,Ь) , равно в точности N _a N _ъ .

Пусть G = (V, Е) - связный граф с N вершинами и Т = (VТ, ЕТ) - произвольное его поддерево. Выберем в Т произвольную вершину v Е VТ такую, что найдется ребро e‘ = (v,u) Е ET. Присоединив к T это ребро, мы получим новое поддерево Т‘ = = (VT‘,ЕТ') = (VT U {u}),ET U {е‘}. Определим также функцию h : VT ^ R на вершинах х Е VT дерева T по формуле

h( ^x ) = £ \ ^xv \ t .

y & VT

Имеет место следующая лемма.

Лемма 1. Справедлива формула

W (T ') = W (T) + h(v) + w(e')|VT |, где \VT| - число вершин в поддереве T.

Доказательство. Из формулы (3) следует

W (T ‘) =  £  w(e)WX + wXjNX, e=(a,b)tET

Здесь через N '_a ,N b ,N,N '_U , как и выше, обозначены числа вершин в поддеревьях дерева T ’ после удаления соответствующего ребра. Не ограничивая общности, будем предполагать, что ребра (а,Ь) заданы так, что v Е T^ (см. рис. 1). Тогда

N a = N a , N b = N b + 1.

Поэтому

W (T ‘)=  £  w(e)NaNb +  £  w(e)Na + w(e' )NN = e=(a,b)GET                e=(a,b)GET

= W (T )+   £   w(e)N a + w(e' )NN.

e=(a,b) G ET

Заметим, что число путей, ведущих из вершины а Е VT в вершину v через ребро (а,Ь) , равно N _a . Так, что

£    w(e)N a = h(v).

e=(a,b) E ET

Замечая, что N ^ = | VT | , N a = 1 , приходим к требуемому.

Идея алгоритма построения приближенного решения вариационной задачи (2) заключается в том, чтобы к построенной части T искомого дерева добавить новое ребро, дающее, по возможности, минимальный прирост индекса Винера. Заметим, что прирост индекса Винера при добавлении нового ребра e' = (v, и) равен

h(v)+w(e' ) \ VT | .

При каждом фиксированном v Е VT минимум этой суммы достигается для вершины и , дающей ребро с минимальным весом. Это дает нам следующую последовательность

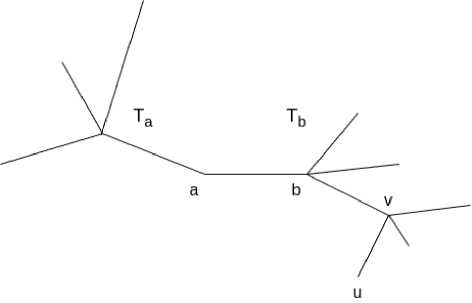
Рис. 1. К доказательству леммы 1

действий. Для каждой вершины v Е VT обозначим через p. (v) Е V вершину ближайшую, то есть с наименьшим весом w(e ' ) , смежную с v и не принадлежащую VT . Теперь на множестве вершин х Е VT определим функцию

д(х) = h(x) + w((х, ^ (х))) • | VT | .

Искомой вершиной для присоединения нового ребра (х * , ц (х * )) к дереву T будет точка минимума функции д(х)

х * = argmin^ yy д(х).

Для поиска точки минимума этой функции строим матрицу Р размера | VT | х | VT | , в i -й строке которой содержится величина длины пути от нее до j -й вершины. Затем для каждого г = 1, 2,..., | VT | вычисляем сумму элементов этой матрицы и величину w((i, ^ (i))) . В полученном массиве находим минимальное значение. Так, что номер искомой вершины вычисляется по формуле

/\vt |                        \

i * = argmin i I ^ P ij + w((i, ^ (i))) I .                         (4)

3=1

Матрица Р = \\ P ij || вычисляется посредством алгоритма Дейкстры.

4.    Вложение слов

Помимо вычисления индекса графа текста, мы будет вычислять индекс Винера для евклидова вложения графа. Для этого нам понадобится построить отображения некоторого достаточно большого словаря слов естественного языка в многомерное евклидово пространство. Пусть V обозначает множество слов этого словаря, L = | V | - мощность этого множества. Искомое отображение f : V ^ R ” можно строить различными способами. Это одна из проблем компьютерной лингвистики, и в литературе носит название «проблема вложения слов» или «проблема векторизации слов». В качестве примера приведем формулы для вычисления так называемой TF — IDF характеристики, которая позволяет приписывать словам векторы евклидова пространства. Рассмотрим несколько текстов как документов D 1 , D 2 ,..., D _m . Для заданного слова w Е V вычислим следующие величины

TF(w,D _i ) = частота слова w в документе D _i .

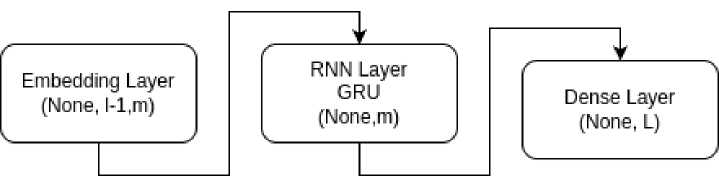
Рис. 2. Архитектура нейронной сети

IDF (w) = log

M число документов, содержащих w

Наконец, характеристика TF о IDF(w,D i ) вычисляется так:

TF о IDF(w, D i ) = TF(w, D i ) • IDF(w).

Таким образом, получаем вложения слов из коллекции документов в векторное пространство размерности M . Полученное таким образом вложение слов из словаря V может быть использовано во многих задачах, связанных с классификацией текстов. Однако для решения задач выявления информативного текста данная характеристика плохо подходит, поскольку не учитывает структуру текста, последовательность следования слов. Поэтому мы будем использовать другие способы векторизации слов. Один из таких способов построения вложения слов описан в статье [10]. Этот метод основан на обучении нейронной сети, представленной на рисунке 2.

Первый слой Embedding во время обучения сохраняет текущие значения коэффициентов искомой матрицы отображения вложения слов. На вход этому слою подаются унитарные коды последовательности слов текста. Более подробно это выглядит так. Пусть w 1 ,w ₂ , ...,w i - очередная порция последовательно расположенных слов текста. Заменим каждое слово w j ,j = 1,2,...,/ его унитарным представлением, то есть вектором v(w j ) Е R ^l , в котором компоненты равны нулю, кроме одной, чей номер равен номеру слова w j в словаре. Соответствующая компонента равна 1. Обозначим через А Е M _m,_L матрицу весов первого слоя. Здесь т - это размерность вложения. Тогда этот слой вычисляет векторы

Z j — А • v(w j ), Z j Е R , j — 1, 2,..., I — 1.

Следующий рекуррентный слой выполняет усреднение полученных векторов и выдает один вектор z Е R ^m размерности вложения. Последний плотный слой вырабатывает вектор размерности, равный размеру словаря, то есть вектор у Е R ^L . В процессе обучения минимизируется ошибка

• ⁵= Е |у^{— v(w}i^)|2,

5.    Обучение модели распознавания информативного текста

где сумма вычисляется по всем наборам слов w1,w2, ...,wl заданного текста. Таким образом приведенная нейронная сеть обучается предсказывать следующее слово, то есть по словам w1, ...,wl-1 предсказать слово wl. Результатом обучения данной нейронной сети является матрица весов А первого слоя. Именно эта матрица и задает вложение f : V ^ Rm. Столбец с номером j этой матрицы соответствует т координатам вложения j-го слова из V. В нашем исследовании мы воспользовались готовой такой матрицей, взятой с ресурса RusVecto¯ re¯ s . Эта матрица извлекается из текстового файла, в каждой строке которого записано слово и координаты его вложения. Размерность вложения т = 300, размер словаря L = 237 255.

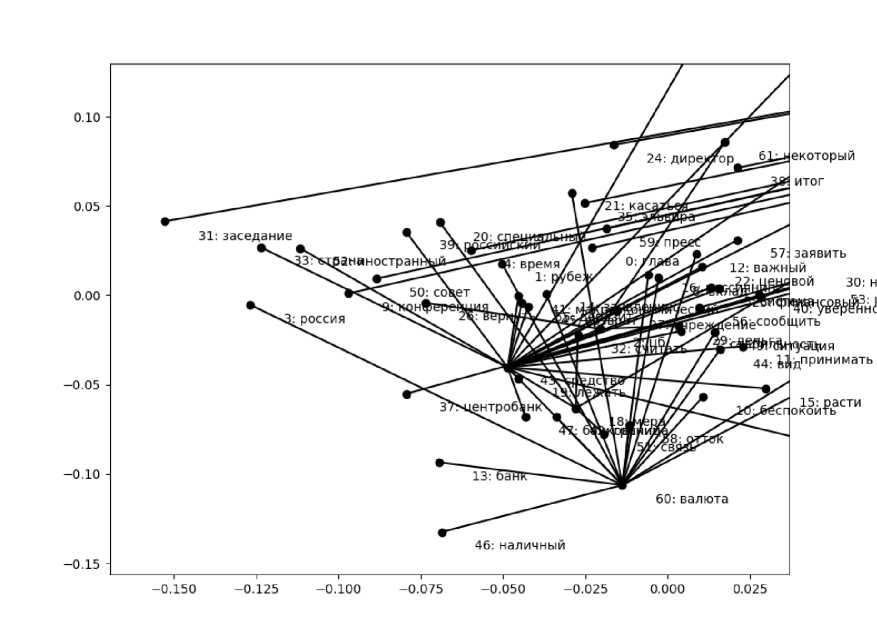
Рис. 3. Пример части дерева, формируемого представленным в § 3 алгоритмом

Часть дерева, построенного приведенным в § 3 алгоритмом для реального текста, с учетом вложения слов, показана на рисунке 3. Это проекция плоского дерева на случайную двумерную координатную плоскость 300-мерного пространства, в которое вложены слова словаря. Номер перед словом на графике соответствует номеру слова в словаре, составленному по исходному тексту.

Для обучения использовался набор размеченных текстов на два класса: 873 информативных текстов и 864 неинформативных текстов. Можно считать выборку сбалансированной. Эти тексты были подготовлены и размечены нашими коллегами с кафедры теории и практики перевода и лингвистики Волгоградского государственного университета. Для каждого текста были вычислены следующие характеристики.

• •    Первые две величины х 1 ,х ₂ вычисляются для конечного множества точек, которое строится так. Заданный текст U разбивается на отдельные предложения, а каждое предложение - на слова. Далее, используя матрицу А вложения слов, вычисляем координаты каждого слова каждого предложения. Напомним, как это делается. Очередное слово текста (за исключением стоп-слов) имеет номер j в словаре языковой модели, взятой с указанного выше ресурса RusVectores. Матрица А умножается слева на вектор унитарного представления этого слова – то есть на вектор, составленный из нулей и одной единицы в j -й компоненте. Затем для всякого предложения вычисляем геометрический центр вложений его слов. В результате

  №	Модель ML	Точность, %
  1.	Наивный байесовский классификатор	78
  2.	Метод опорных векторов	70
  3.	Метод k ближайших соседей, k = 5	70
  4.	Метод решающих деревьев	69
  5.	Квадратичный дискриминатор	75
  6.	Случайный лес	75

получается конечное множество, число элементов которого равно числу предложений в тексте. Для полученного конечного множества строим дерево Т с помощью алгоритма, описанного в предыдущем разделе, используя в качестве графа полный граф построенного конечного множества геометрических центров вложений слов предложений. Наконец, вычисляем величины х 1 = W _n (T ), х ₂ = W _e (T ) .

• •    Третья величина х ₃ вычисляется как значение W _n (T ) для дерева Т , построенного алгоритмом из предыдущего раздела. При этом в качестве графа выбирается граф G u текста U с весами ребер, равными 1.

• •    Четвертая величина х ₄ вычисляется как величина W _n (T ) для минимального остов-ного дерева Т в графе G u .

Каждой такой четверке приписывается метка у =1 , если текст классифицируется как информативный и значение у = 0 - в противном случае. Обработанные таким образом наборы текстов генерируют два множества, представленные матрицами X Е Е М _к,4 , Y Е М _к,1 , где К - общее число текстов.

Надо заметить, что предварительно из текстов были удалены стоп-слова. С этой целью авторы воспользовались библиотекой NLTK. В качестве моделей машинного обучения выбраны следующие методы:

• •    Наивный байесовский классификатор с гипотезой нормального распределения.

• •    Метод опорных векторов.

• •    Метод к ближайших соседей.

• •    Метод решающих деревьев.

• •    Квадратичный дискриминатор.

• •    Случайный лес.

6.    Программная реализация

Обучающий и тестовый наборы данных были поделены в отношении 2 : 1. Точность предсказания перечисленных моделей представлена в таблице выше. Данные из этой таблицы представляют собой усредненные значения по серии экспериментов. На каждом эксперименте обучающий и тестовый набор данных формировались заново, после случайного перемешивания всего датасета.

Лучший результат для байесовского классификатора вполне объясним. Дело в том, что в качестве признаков используются различные варианты индекса Винера, которые представляют собой суммы длин кратчайших путей. Принимая гипотезу о том, что длины таких путей имеют одинаковое распределение и используя центральную предельную теорему, можно сделать вывод о том, что величины х 1 , х ₂ , х ₃ , х ₄ имеют распределение, близкое к нормальному.

Представленный в статье алгоритм реализован в виде отдельного пакета Word Graph на языке программирования Python. Для поиска кратчайших путей во взвешенном графе использовался пакет scipy.sparse.csgraph. В этом пакете имеются реализации нескольких алгоритмов. В своих расчетах мы использовали реализацию алгоритма Дейкстры. Этот же пакет использовался для поиска минимального остовного дерева во взвешенном графе. Также в этом пакете имеется реализация алгоритма вычисления компонент связности произвольного графа G = (V, Е ) , которая необходима для корректного вычисления индекса Винера. Все матричные представления графов и результатов вычислений на них использовали массивы из пакета numpy. В частности, для поиска решения задачи на минимум (4) была применена функция numpy.argmin пакета numpy.

С целью решения задачи классификации текстов использовалась библиотека машинного обучения scikit-learn. При этом вышеупомянутые массивы X, Y , созданные по набору текстов, были упакованы в файл формата NPZ. Этот формат используется специально для хранения больших numpy массивов на диске, и для работы с таким форматом имеются пакеты как для языка Python, так и для языка программирования Go.

Все тексты программ, файл массивов X, Y, а также частичный набор текстов доступны свободно в репозитории по ссылке: Для загрузки исходного кода необходимо в терминале выполнить команду

Для использования скачанных текстов программ дополнительно понадобится скачать с ресурса языковую модель tayga_1_2 и разместить соответствующий файл в каталоге data. Для индексирования слов из этой модели с целью ускорения вычисления вложений слов необходимо установить значение build_index=True в вызов метода