О возможности оценки геометрических характеристик астероида по радиолокационному портрету

DOI:

В настоящее время традиционные оптические астрономические средства наблюдения дополняются возможностями радиолокационной астрономии. Средства и методы радиолокационного зондирования позволяют получать новую информацию о космическом объекте [6]. Так, например, радиолокационные средства дополняют оптические методы возможностью проводить наблюдения вдоль продольной координаты по лучу зрения. В частности, при высоком разрешении появляется возможность строить трехмерные модели космических объектов [2].

При радиолокационном зондировании под сверхвысоким разрешением понимается выполнение условия, при котором разрешающий элемент (по дальности) существенно меньше линейных размеров объекта. В радиолокации элемент разрешения определяется длительностью основного лепестка функции автокорреляции зондирующего сигнала. Высокое разрешение по дальности (по лучу зрения) при радиолокационном зондировании достигается использованием как коротких импульсных радиосигналов, так и ква-зинепрерывных частотно-модулируемых сигналов [3]. В данной работе мы остановимся на первом варианте, как наиболее простом при технической реализации. Использование сверхвысокого разрешения позволяет строить «радиолокационные портреты» объекта. Под радиолокационным портретом понимается отраженный от цели сигнал, пространственный размер которого по лучу зондирования много меньше линейного размера объекта.

Будем полагать, что объект имеет протяженность большую по сравнению с элементом разрешения локатора. Так, например, при полосе частот сигнала А/ ^ 100 МГц элемент разрешения Аг составляет величину 1,5 м. Характерные размеры зондируемых околоземных астероидов составляют 10–100 м. Таким образом, при подобном соотношении размеров условие сверхразрешения выполняется.

Целью работы является изучение возможностей оценки основных геометрических параметров малых небесных тел радиолокационными средствами.

Мы ставим задачу анализа возможностей восстановления геометрических характеристик (формы) космических объектов [9] исходя из данных, полученных путем решения прямой задачи обратного рассеяния сверхразрешающих сигналов на модели астероида относительно простых форм.

В качестве геометрической модели астероида мы принимаем одноосный эллипсоид при произвольной ориентации его относительно луча зрения или пару соединенных друг с другом сфер разных размеров (раздел 1).

Мы пользуемся подходом технической электродинамики при решении задачи дифракции на поверхности отражающих тел. Интеграл Стрэттона — Чу [4] обобщен нами на предмет учета эффекта Доплера. Квадратура может быть рассчитана численно для различных комбинаций значений управляющих параметров задачи. Однако мы предпочитаем ограничить рассмотрение откликом мишени на бесконечно короткий сигнал. В таком случае отраженный сигнал представляет собой импульсную характеристику зондируемого объекта. Импульсная характеристика является устойчивой относительно трансляционных и масштабных преобразований объекта [8]. По ней можно восстановить реакцию объекта на произвольный сигнал конечной длительности. В настоящей работе мы изучаем возможность восстановления формы и геометрических особенностей малых небесных тел по их импульсным характеристикам.

Результаты расчетов и их обсуждение приведены в разделе 2.

Вывод о потенциальной возможности оценивания геометрических характеристик малых небесных тел методом радиолокационного зондирования приведен в Заключении.

• 1.    Отражение широкополосного радиосигнала от поверхности астероида. Геометрия задачи и основные уравнения

  1.1.    Форма и кинематика астероида

Полагаем астероид движущимся поступательно со скоростью V , при этом лучевая компонента скорости равна V (если V < 0, то астероид движется к наблюдателю). Здесь ось г задает направление распространения зондирующего радиосигнала. Скорость V , разумеется, мала по сравнению со скоростью света с.

Аппроксимируем форму астероида c выпуклой поверхностью эллипсоидом с полуосями а, Ь, с (считаем далее по умолчанию а >  Ь >  с, однако, в разделе 2 это ограничение снимаем); ось ж повернута так, чтобы лежать в плоскости, образуемой осью г и наибольшей полуосью. Начало системы координат считаем совмещенным с центром О объекта в момент t = 1 а прихода к объекту зондирующего сигнала.

Имеем номинально три кинематических параметра, характеризующих поступательное движение: V = ( V _x ,V _y ,V _Z ), причем все три компоненты скорости астероида в общем случае ненулевые. Однако поперечное движение при нерелятивистских скоростях приводит к плохо наблюдаемому поперечному эффекту Доплера, поэтому поперечными компонентами далее пренебрегаем и полагаем ( V _x ,V _y ) = 0. Таким образом, от поступательного движения остается единственный параметр V _z .

Введем позиционный угол Ф между отрицательным направлением оси г и направлением большой полуоси (см. рис. 1).

Для расчетов используем сферическую систему координат, связанную с центром астероида О. Введем полярный угол 0 между отрицательным направлением оси г и направлением на произвольную точку на поверхности астероида и азимутальный угол Ф в картинной плоскости, отсчитываемый от оси х (рис. 1).

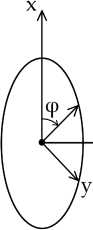
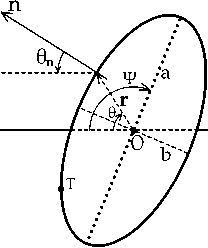
Рис. 1. Схема прохождения фронта радиоволны по астероиду. Показано вертикальное сечение астероида

Для параметризации координат точки на поверхности трехосного эллипсоида вводим широту и долготу трехосного эллипсоида для определения декартовых координат в повернутой и совмещенной с главными осями эллипсоида системе декартовых координат по стандартным правилам [5]. Явный вид всех геометрических соотношений в общем случае опускаем в силу их громоздкости. Далее в примерах расчета интегралов приводим только выражения для частных случаев совмещения оси визирования с главной осью.

Таким образом, имеем четыре геометрических параметра модели астероида в форме эллипсоида:

• •    позиционный угол Ф;

• •    два эксцентриситета е 1 = ^/ 1 — b ² Jo ² , е ₂ = ^ 1 — с ² Jo ² ;

• •    общий характерный размер астероида, пропорциональный наибольшей полуоси о.

Модель астероида c невыпуклой поверхностью задаем в форме «снеговика» как два соединенных друг с другом шара радиусами R 1 и R 2 (R 1 < R 2 ), ось между центрами которых расположена под некоторым углом к оси визирования (см. рис. 2).

1.2.    Зондирующий радиосигнал

Будем полагать, что зондирующий сигнал представляет собой короткий радиоимпульс, распространяющийся по лучу зрения вдоль оси г .

Энергия той части зондирующего сигнала, которая будет огибать астероид и рас- сеиваться на нем, равна

ДЕ О = S

∞

∞

| u o (г, ^) | ² dz,

где S — площадь поперечного сечения астероида (см. рис. 2).

Форму огибающей сигнала примем в виде гауссианы:

U o ( z,t) = Л о exp

^{[ z} - Z o ^- c ( t ^- t o ^)] 2 AZ 2

где Л _о — комплексная амплитуда; t ₀ , z ₀ — начала отсчета зондирующего импульса;

△ z ₀ — пространственный размер импульса. Тогда выражение (1) сводится к виду:

M Z = 'Д ^{5 |4}-1 2 -

Предельный случай радиолокационного портрета при Az ₀ ^ 0 представляет собой импульсную характеристику. Другими словами, под импульсной характеристикой объекта в радиолокации понимается реакция объекта на его облучение импульсной волной. Это позволяет нам в расчетах принимать огибающую зондирующего сигнала, как обладающую свойствами дельта-функции, что упрощает расчеты. Следовательно, рассчитываемый нами отраженный объектом сигнал следует рассматривать как импульсную характеристику объекта.

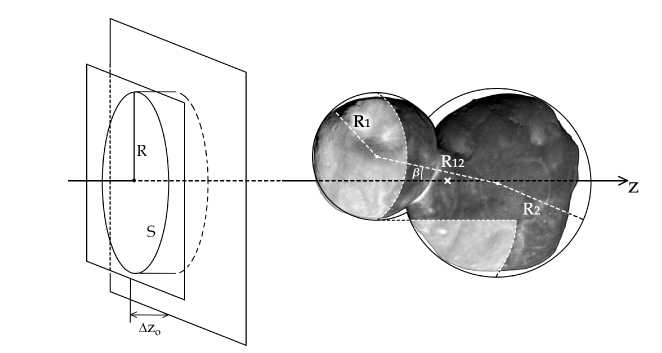
Рис. 2. Структура зондирующего радиоимпульса и участки экспонируемой поверхности астероида на примере модели астероида 486958 Arrokoth.

На рисунке выделены экспонируемые и затененные области поверхности астероида

1.3.    Прохождение зондирующего сигнала по астероиду

Момент обратного рассеяния (отражения) фронта сигнала зависит от того, в какой части поверхности происходит отражение (напомним, что отражающая поверхность — не плоская).

В случае, когда астероид развернут одной из главных полуосей вдоль линии визирования, отражение происходит от эллиптических кольцевых слоев на экспонируемой поверхности астероида с последовательным увеличением размера эллипса от нулевого в точке встречи сигнала с поверхностью до максимального вплоть до момента ухода сигнала в тень.

В случае произвольного ракурса под большим углом к линии визирования отражение происходит последовательно от криволинейных кольцевых слоев. Первой начинает отражать «макушка» астероида (точка Т на рисунке 1), затем размеры колец последовательно возрастают. В дальнейшем после пересечения терминатора (для эллипсоида на рисунке 1 терминатор проецируется на пунктирную линию) кольца перестают быть замкнутыми и по достижении диаметрально противоположной позиции на терминаторе исчезают, после чего фронт волны уходит в область тени и перестанет освещать астероид.

1.4.    Обратное рассеяние радиосигнала

Амплитуду отраженного сигнала обозначаем как и 1 ( r,z, Ф, £) в цилиндрической системе координат (рис. 1).

Отраженные от поверхности в разных направлениях электромагнитные волны рассеиваются в верхней (относительно отражающего элемента поверхности) полусфере (см. рис. 3). Относительную интенсивность рассеяния задает функция 5(0 0 ,0 1 ), где 0 0 — угол падения; θ 1 — угол рассеяния.

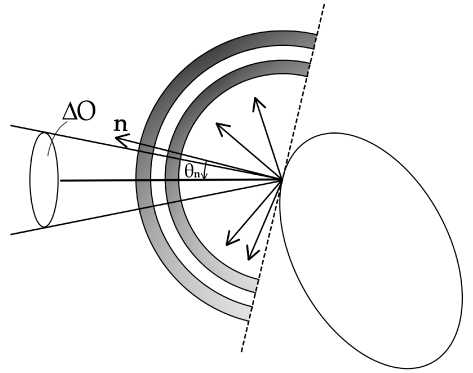
Рис. 3. Схема рассеяния радиоволны от поверхности астероида

Нас в задаче интересует обратное рассеяние, когда 0 1 = 0 0 = 0„. Вместо функции двух аргументов в радиолокационной астрономии определяют функцию обратного рассеяния как функцию одного аргумента. Ее часто аппроксимируют зависимостью [1; 7]

5(0 _П ) = 0, 5о о (n + 1)cos ⁿ 0 _П , (4)

где о ₀ — радиолокационное альбедо поверхности; n — фактор гладкости поверхности, который, как правило, выбирают в диапазоне 1 < n <  10. В своей работе мы используем значение n = 1,8 из работы [1], в которой показано, что данное значение является оптимальным.

Зависимость (4) пишется для интенсивности. Для амплитуды тогда соответствующую зависимость нужно переопределить следующим образом:

о(0п ) = //о, 5оо (n + 1) егх cosn/2 0п, (5) где егх есть некоторый фазовый множитель, зависящий от материала отражающего тела. Если фазовый угол х не зависит от угла рассеяния, то фазовый сдвиг егх одинаков для всех точек поверхности и, стало быть, является общим множителем в решении, который не существенен и его можно отбросить, так как смысл имеет разность фаз, а не абсолютная фаза. Таким образом, далее полагаем х = 0.

1.5.    Эффект Доплера: оценки

В теории радиолокации хорошо известно приближенное выражение для изменения частоты при продольном эффекте Доплера для медленно по сравнению со скоростью света движущихся целей

^V 1 = 1 - 2 ^V . (6)

V 0 с

Для типичных для радиолокационной астрономии параметров | V _z | ^ 1 — 10 км/с, Д ~ ~ 100 м и частоты зондирующего широкополосного сигнала v ₀ ^ (3 — 10) • 10 9 Гц имеем

| Av | = | v i - v o | = 2v o ^ (0, 02 - 0,6) МГц. (7) с

Изменение энергии отраженного сигнала за счет эффекта Доплера при |V_z | ^ ^ с мало и мы этим изменением пренебрегаем по сравнению с потерями энергии при рассеянии на не идеально белой поверхности астероида.

1.6.    Расчет отражения радиосигнала от поверхности астероида. Учет эффекта Доплера

С учетом того, что V | ^ с, сохраним член только первого порядка в разложении выражения для амплитуды отраженного сигнала, получаемый из интеграла Стрэттона — Чу [4]. Кроме того, при выводе приходится использовать компромисс между представлением зондирующего сигнала в виде переменной во времени волны, то есть учитывать конечный продольный по лучу зрения размер сигнала, и представлением сигнала бесконечно узким импульсом, устремляя его продольный размер к нулю.

Выведем выражение для отраженного сигнала. Для простоты изложения ограни- чимся случаем, когда эллипсоид осесимметричен и расположен полуосью а вдоль оси визирования (то есть в данном частном случае Ф = 0).

Пусть в момент времени t = 1 a волна касается эллипсоида в его передней точке Т , которая лежит на оси визирования. Уравнение движущегося эллипсоида имеет вид (здесь и далее используем цилиндрический радиус г)

( z - V_z (t - t _A )) 2 г ² _ а ^{2        +} 6 2 =

Положение бесконечно короткого радиоимпульса в произвольный момент времени t на оси z есть z, (t) = —а + ct.                                     (9)

В этот момент импульс освещает на эллипсоиде бесконечно тонкое кольцо радиуса г,(,) = 61 - (z,(О -^ - ,А»’

= ⁶ F-

^{(( c - V} z ^)(t — ^t A ^{) - а )} 2 а ²

Падающая на астероид зондирующая волна распространяется без искажения своей формы в среде без дисперсии (вакуум), ее пространственно-временная эволюция всюду в пространстве вне астероида описывается выражением для бегущей волны

,   .       / г — ct \

«о^^ :    у

Отраженный от астероида сигнал подвергается сжатию/растяжению (Аго ^ Аг1) вследствие эффекта Доплера и, кроме того, появляется фазовый сдвиг δ. Рассеянный назад сигнал уже не является фрагментом бесконечно узкого плоского слоя (см. рис. 2), его профиль очерчивает профиль астероида, слегка искажаясь вследствие смещения астероида за тот малый промежуток времени, пока зондирующий сигнал проходит по поверхности астероида. Распространяющийся рассеянный назад сигнал следует описы- вать функцией

« 1 (г, Г, t) = « 1

—г — ct

V Аг о

+ 5,г),

где фазовый сдвиг 5 является функцией момента отражения t, вследствие равномерности движений импульса и астероида, очевидно, линейной, а г = г ( г ) определяется из уравнения движущегося эллипсоида (8).

На передней точке Т рассеивающей поверхности, в которой в исчезающе малый, но все еще конечный промежуток времени в окрестности момента времени t _A происходит рассеяние, падающий и отраженный сигналы в любой момент времени должны оставаться пропорциональными друг другу с коэффициентом пропорциональности, выражающим отражательные свойства поверхности:

-и 1 ( г А ( € ) , 0, t) = сг(О)и о (г л (t), t).

Это означает, что временные зависимости (11) и (12) на движущейся границе г = £ а (^) должны быть одинаковыми, из чего вытекают два равенства.

Первое следует из известного соотношения для эффекта Доплера:

Аг 1 = Аг _о

c + V c — V ’

второе определяет сдвиг фазы

2c а + V , t _A

Аг о c + V ,

Таким образом, рассеянный назад от точки Т сигнал имеет вид:

« 1 (г, 0 ,t ) = о

(0) «о (

c — V , г + ct c + V , Аг о

-

2c а + V , t A Аг о c + V ,

.

Найдем рассеяние от остальных точек экспонируемой поверхности эллипсоида вне оси визирования. Аналогичным образом заключаем, что на рассеивающей поверхности, в точке с координатами г / (t), r j (t) между падающим и отраженным сигналом так же, как и в передней точке, в любой момент времени сохраняется пропорциональность:

«1(г/ (t),rJ(t),t) = о(9n(t))uо(гJ(t),t), где

cos 0 „ (t) =

^           ^z , ^{( t )} - ^V z ^{( t} - ^ A )

^ - ( ^"-" ) ^(z , ^{( t )} - ^V z ^{( t} - ^t A ⁾⁾ 2

косинус угла, под которым в момент времени t происходит обратное рассеяние.

С учетом того что точка, в которой происходит обратное рассеяние, равномерно перемещается по поверхности эллипсоида вдоль оси z, для сигнала, отраженного от кольца конечного радиуса, фазовый сдвиг оказывается линейно зависящим от времени:

5(t) = - 2с

( а + ^ct A ) ^{- t(c} — V , ) Az o (c + V _z )

Результирующий отраженный сигнал собирается интегрированием по поверхности астероида по всему сечению S астероида

Ui(t) = У ui(z,r(z),t)2nrdr = У Ui(z,rf (t),t)2nr,(t) cos(0n(t)) V^+cdiydz, здесь производная ^, вычисляется из соотношения (8).

Собирая вместе (9), (10), (12), (18)–(19), осуществляя предельный переход к δ-функции при Az0 ^ 0 и интегрируя зондирующий сигнал (5-функцию) по z, получаем выражение для отраженного сигнала:

U i (t) = 2n ^ 0.5oo(n + 1)6 2 [1 -

^{(( c -} V_z^)(t — ^t A ^{) - a )} a ²

² ] 1 ^/2 X

X ( - O L [ z , (t) - V , (t - t A )] ) " ^{+ 1} ( 1 - ( ° 2^ ) (z , (t) - V , (t - t A )) ² ) ⁴ . (21)

Данное выражение описывает не сосредоточенный, как требуется для импульсной характеристики, а распределенный вдоль оси z отраженный сигнал. А именно, величина U 1 ( t ) в (21) определяется как сигнал, отраженный в момент времени t в точке z = z , (t). Для восстановления импульсной характеристики следует собрать отраженный сигнал в апертурной плоскости, например, в точке z = - а, учтя при этом время задержки сигнала (время, требующееся отраженному в момент времени t в точке z = z , (t) сигналу для возвращения в точку z = - а). Для этого в выражении (21) следует сделать замену ^{( t - t} A ⁾ ^ ^{( t - t} A ^{) /} 2.

В расчетах мы полагаем t A = 0.

2.    Результаты моделирования

Как показали расчеты, импульсная характеристика отражающего тела сильно зависит от его асферичности.

Рассмотрим семейство импульсных характеристик (21) эллипсоидов в зависимости от степени их сплюснутости/вытянутости.

Импульсная характеристика сферы демонстрирует резкий всплеск, обусловленный отражением от окрестности передней точки сферы («блестящей точки») (см. рис. 4).

Снижение интенсивности отраженного сигнала от момента достижения максимума до полного затухания сигнала длится примерно 80 % от полной длительности отраженного сигнала (рис. 4a). Рисунок 4b указывает на экспонируемые части поверхности сферы области, вносящие соответствующий вклад в отраженный сигнал.

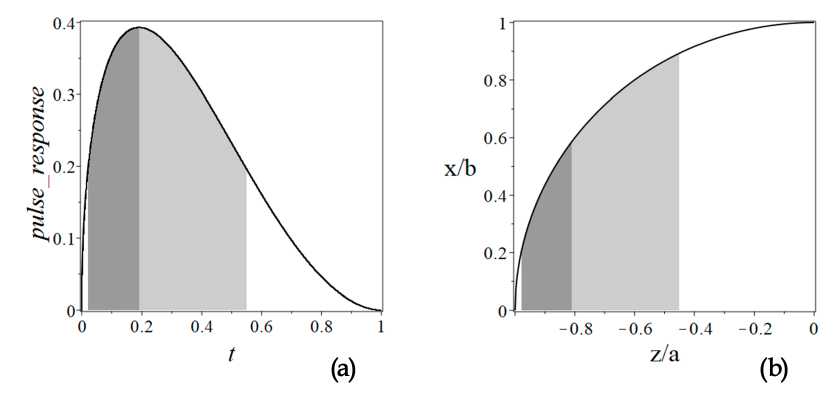
Рис. 4. ( a ): импульсная характеристика в относительных единицах для модели сферического астероида (а = b). Время нормировано на длительность прохождения зондирующего импульса по астероиду. Астероид движется навстречу наблюдателю с относительной скоростью | V ^ | /с = 10 -5 . Функция обратного рассеяния задается формулой (5) c п = 1,8.

Темно-серым цветом отмечен промежуток времени, при котором амплитуда отраженного сигнала нарастает от половины максимального значения до максимума, светло-серым — промежуток времени, при котором амплитуда спадает от максимума до половины максимального значения.

За эти промежутки времени зондирующий импульс пересекает участки поверхности астероида, отмеченные теми же соответствующими цветами (рисунок ( b ))

Семейство импульсных характеристик на рисунке 5a соответствует различным степеням сплюснутости и вытянутости эллипсоида. Мы фиксируем протяженность астероида по лучу зрения (полуось а) и варьируем поперечный размер тела (полуось Ь). При этом увеличение сплюснутости эллипсоида эквивалентно увеличению площади поперечного сечения астероида (полуось Ь растет при неизменной величине длины полуоси а). Это, соответственно, приводит к увеличению амплитуды отраженного сигнала. Максимально вытянутому астероиду соответствует нижняя кривая, максимально сплюснутому — верхняя кривая.

На рисунке 5a показано, что изменение соотношения Ь/а не только приводит к росту/снижению амплитуды, но и к изменению профиля импульсной характеристики. В первую очередь здесь следует отметить изменение положения максимума зависимости U 1 (t). Зависимость положения максимума импульсной характеристики от степени сплюснутости эллипсоида Ь/а показана на рисунке 5b и заметно отличается от прямой. Эта зависимость позволяет восстановить соотношение продольных и поперечных размеров астероида.

Мы считаем, что этот результат является принципиально новым в радиолокационной астрономии. В отличие от используемых в практике длительных последовательностей сигналов, позволяющих восстановить соотношение размеров по полученным кривым блеска, наш подход позволяет чрезвычайно быстро находить искомую геометрическую характеристику астероидов в режиме моноимпульсной локации. Для сравнения, регистрация кривой блеска астероидов, как правило, занимает часы или многие сутки, в то время как импульсная локация позволяет получить результат за минуты или десятки секунд.

Второй важный вывод, вытекающий из нашего рассмотрения, заключается в том, что если объект содержит несколько блестящих точек, то в радиолокационном портрете следует ожидать нескольких всплесков, временное положение которых будет коррелировать с расположением доминирующих центров отражения (рис. 6). По наличию всплесков импульсной характеристики можно предположить наличие двояковыпуклых фрагментов рассеивающей поверхности, что позволяет приблизительно оценить форму объекта.

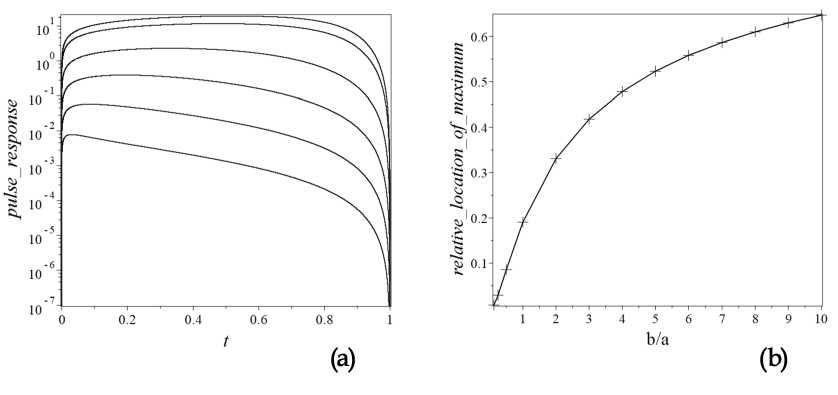
Рис. 5. ( a ): импульсные характеристики в относительных единицах в логарифмическом масштабе для модели эллипсоидального астероида (полуось а расположена вдоль оси визирования, полуось b — поперек). Скорость астероида и параметры функции рассеяния — те же, что и для случая, представленного на рисунке 4. Кривые соответствуют следующим значениям сплюснутости/вытянутости астероида b/а, снизу вверх: 0,125; 0,25; 0,5; 1; 2; 4. ( b ): момент времени, отвечающий максимальному значению импульсной характеристики, в зависимости от степени сплюснутости/вытянутости астероида

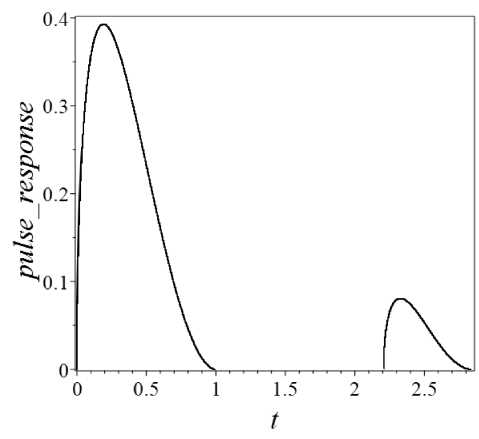
Рис. 6. Импульсная характеристика для модели невыпуклого астероида, изображенной на рисунке 2. Скорость астероида и параметры функции рассеяния — те же, что и для случая, представленного на рисунках 4–5

Заключение

Рассмотрена задача дифракции радиолокационного сигнала на малом небесном теле эллипсоидальной формы или составленного из двух соединенных друг с другом сфер. Для различных конфигураций рассчитана импульсная характеристика объекта. На примерах продемонстрирована возможность оценки параметров формы объекта при зондировании широкополосными сигналами с различных ракурсов.