О возможностях спектральной эллипсометрии для исследования параметров плазмы крови больных хроническим панкреатитом. Полный факторный эксперимент

Эллипсометрия — это бесконтактный и неразрушающий оптический поляризационный метод исследования поверхности твердых тел и жидкостей, обладающий сверхчувствительностью к изменению состояния поверхности. Это делает данный метод весьма перспективным для его использования в медицине для диагностики различных заболеваний. В последние годы появились сообщения об использовании метода эллипсометрии для определения параметров тонких пленок, полученных центрифугированием плазмы крови человека на твердую подложку, в целях диагностики цереброваскулярной патологии и заболеваний печени [1, 2]. При хроническом панкреатите такие исследования не проводились. Однако тонкие пленки плазмы крови, полученные на кремнии или другой твердой подложке с помощью центрифуги, несут на себе довольно сильный отпечаток свойств поверхности подложки, имеющей довольно сложную структуру. Гораздо более перспективными являются исследования жидкой фазы плазмы, не связанные с использованием какой-либо твердой подложки. Жидкая плазма также обладает поверхностной структурой в виде некоторого поверхностного слоя. Толщина и оптические параметры этого слоя зависят от выраженности заболевания. Метод эллипсометрии, обладающий сверхчувствительностью к изменению состояния поверхности, реагирует на это заметным изменением измеряемых поляризационных углов Ψ и Δ .

Целью данной работы является выявление реальных возможностей метода эллипсометрии для исследования плазмы крови в целях диагностики хронического панкреатита. При этом плазма используется в виде жидкой фазы. Обработка результатов эллипсометрических измерений проводится с помощью статистического метода полного факторного эксперимента [3, 4].

1. ВЫБОР МОДЕЛИ ОТРАЖАЮЩЕЙ ПОВЕРХНОСТИ ОБРАЗЦА

При исследовании различных образцов большое значение имеет правильный выбор модели поверхностной структуры образцов. Если поверхностная структура является результатом технологических процессов по нанесению пленок того или иного типа на однородную подложку, то выбор модели этой структуры не является особой проблемой. Если же речь идет об исследовании поверхности однородных по составу материалов, то здесь, как это ни покажется странным, ситуация гораздо сложнее. Казалось бы, наиболее естественной в этом случае является простейшая модель однородного образца с резкой (геометрической) границей. Кратко остановимся на этой модели. При этом основное внимание уделим ее особенностям, проявляющимся при исследовании однородных по составу материалов.

Оптические параметры n и κ однородного образца находятся из соответствующего основного уравнения эллипсометрии tgT exp(iA) = Rp I Rs, (1)

.   . ₂    ,     2 cos²2 T- sin²2 T sin² A

A = sin Ф о 1 + tg Фо            ---—---

_            (1 + sin2 T cos A )

B = sin² Ф о tg² Ф о

sin4 T sin A (1 + sin2 T cos A )²

ϕ ₀ — угол падения светового пучка на поверхность образца; T и A — поляризационные углы, отвечающие подложке.

Для прозрачного однородного образца, когда

к = 0,

углы T и A определяются соотношениями (см., например, [5])

T = 0,            если ф о = ф оь ,       (6)

180°, о или 3бо°,

если ф о <  ф оь ; если ф о >  ф оь ,

где ϕ _0b — угол Брюстера

Шь = ⁿ .               ⁽⁸⁾

где R_p и R_s — комплексные амплитудные коэффициенты отражения для p - и s -волн, зависящие в общем случае от оптических параметров и толщин поверхностных слоев, оптических параметров подложки, а также от длины волны λ , угла падения ϕ ₀ светового пучка и показателя преломления внешней среды. Комплексное уравнение (1) распадается на два действительных уравнения. Измеряя поляризационные углы T и A и решая основное уравнение эллипсометрии (1), можно определить два любых неизвестных параметра отражающей системы. Показатель преломления n и коэффициент поглощения κ однородной подложки, не несущей на себе никаких слоев, определяются известными аналитическими выражениями (см. [5]), которые можно преобразовать к виду

n =

A + V A ² + BB      п/

------------, к = B A , 2              ^{2 n}

Соотношения (6) и (7) определяют (для случая однородного прозрачного образца) особенности в поведении поляризационных углов Т ( ф _о) и A ( ф ₀). На угле Брюстера кривая Т (ф_о) имеет острие, упирающееся в координатную ось ϕ ₀ , а для угла A ( ф ₀) наблюдается скачок величиной в 180°, определяющий идеальную прямоугольную ступеньку (рис. 1). При этом в качестве такой ступеньки может быть выбрана как нижняя, со скачком A от 18о° до о (кривые 1 и 2 на рис. 1), так и верхняя, со скачком A от 18о° до 3бо°, ступенька (кривые 1 и 3). Выбор вида идеальной ступеньки зависит от того, как ведет себя поляризационный угол A при росте пленки на однородной прозрачной подложке.

Если же однородный образец поглощает ( к * о), то особенности для углов T ( ф _о) и A ( ф ₀) приобретают менее выраженный характер. Острие для угла T ( ф _о) несколько поднимается над осью ϕ ₀ и слегка сдвигается вдоль этой оси, а ступенька для кривой A ( ф ₀) размывается в соответствии с величиной коэффициента κ . При этом размытая ступенька для случая однородного поглощающего образца всегда является нижней, т. е. размывание начинается от идеальной нижней ступеньки (кривая 4 на рис. 1).

где

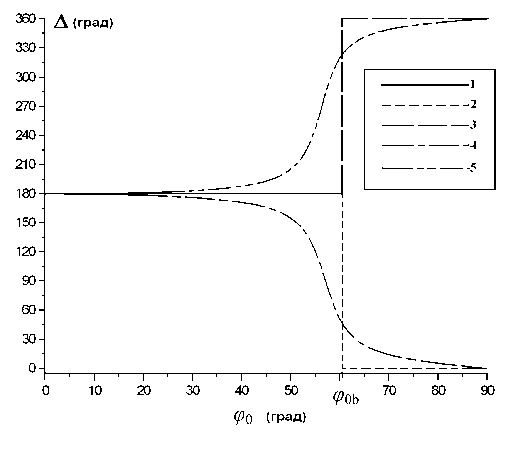
Рис. 1. Графическое представление зависимостей А ( ^ 0 ) в окрестности классического угла Брюстера ϕ _0b .

Кривые 1 и 2 — идеальная прямая нижняя ступенька на угле Брюстера (d = 0); кривые 1 и 3 — идеальная прямая верхняя ступенька ( d = 0); кривые 4 и 5 — размытые нижняя и верхняя ступеньки ( d ≠ 0)

Однако реальный образец всегда в какой-то степени неоднороден. Это обусловлено прежде всего сложной структурой поверхности любого материала. Такая структура проявляется в самых различных формах. Это сверхтонкие пленки естественного окисла на полупроводниках и металлах. Это нарушенные слои на поверхности твердых тел, возникающие в результате той или иной обработки. Кроме того, это также естественная структура поверхности жидкостей, связанная с их общими свойствами и изменяющаяся при добавках различных веществ. Неучтенная поверхностная структура является основной причиной того, что определенные по формулам (2)–(4) оптические параметры однородного по составу материала могут существенно отличаться от значений оптических параметров, определяющих объемные свойства данного материала. Определение параметров поверхностной структуры — это очень важная задача. Но на первом этапе целесообразно оценить влияние поверхностной структуры, не привлекая методы решения математически некорректной обратной задачи. Это можно сделать, используя следующие проявления неучтенного поверхностного слоя.

Как уже указывалось, для однородной прозрачной среды идеальная ступенька для угла А всегда может быть выбрана как верхней, так и нижней. Оба типа ступеньки в этом случае эквивалентны. Для однородной поглощающей среды размытая ступенька всегда является нижней. Наличие поверхностного слоя на однородной подложке меняет ситуацию. Прежде всего, такой слой всегда размывает идеальную ступеньку. Если при этом показатель преломления nf поверхностного слоя удовлетворяет условию nf < n,                     (9)

где n — показатель преломления однородной прозрачной подложки, то ступенька для угла А , размываясь, становится нижней. Если подложка поглощает, то оба эти фактора действуют в одном направлении, превращая идеальную ступеньку в размытую нижнюю ступеньку. А для размытой нижней ступеньки всегда выполняется условие

0 <А< 180°.               (10)

В этом случае, как следует из выражений (2)–(4), эффективный коэффициент поглощения образца с неучтенным поверхностным слоем удовлетворяет соотношению

K ef >  0.                     (11)

Если же показатель преломления nf удовлетворяет условию nf > n,                    (12)

то ступенька для угла А , размываясь, становится верхней. Это всегда имеет место для прозрачной ( κ = 0) подложки, т. е. в этом случае выполняется условие

180° <А< 360°.           (13)

И тогда, как следует из того же выражения (2), эффективный коэффициент поглощения прозрачного образца с неучтенным поверхностным слоем не только становится отличным от нуля, но он еще и отрицателен, т. е. удовлетворяет соотношению

K ef <  0.                    (14)

В то же время поглощение однородной подложки и наличие поверхностного слоя, удовлетворяющего условию (12), действуют в разных направлениях. Это означает, что идеальная ступенька может превратиться как в нижнюю (доминирует поглощение однородной подложки), так и в верхнюю размытую ступеньку (преобладает действие поверхностного слоя). В первом случае эффективный коэффициент поглощения удовлетворяет условию (11), а во втором — условию (14).

Коснемся также вопроса относительно обозначений для эффективных параметров, определяющих оптические свойства однородного по составу материала с неучтенным поверхностным слоем. Если размытая ступенька для поляризационного угла А является верхней, то в этом случае независимо от наличия истинного поглощения у подложки всегда присутствует поверхностный слой, для которого выполняется условие (12), и всегда формулы (2)–(4) определяют отрицательный коэффициент поглощения. Этот результат, если говорить только об оптических свойствах материала, очевидно, не имеет физического смысла. В такой ситуации нет смысла говорить о коэффициенте поглощения или даже его эффективном значении, в этом случае целесообразно ввести аналог ω коэффициента поглощения, также определяемый с помощью формул (2)–(4), в которых делается переход к ^ о. (15)

Если же размытая ступенька для угла А является нижней, то можно говорить и об эффективном значении κ _ef коэффициента поглощения. Что касается показателя преломления, то независимо от вида ступеньки для угла А есть смысл говорить о его эффективном значении n _ef .

Следует обратить внимание еще на одну особенность в поведении параметров n и κ , определяющих оптические свойства однородного по составу материала с неучтенным поверхностным слоем. В общем случае они зависят от угла падения ϕ0 . Этим можно воспользоваться для выявления степени влияния поверхностной структуры. Очевидно, оптические постоянные однородного образца, определенные по формулам (2)–(4), при отсутствии поверхностного слоя не зависят от угла падения ϕ0 . Если же наблюдается такого рода зависимость, и ее нельзя объяснить влиянием экспериментальных ошибок, то это указывает в первую очередь на наличие определенной поверхностной структуры. Выраженность этой зависимости обусловлена величиной оптического контраста между поверхностным слоем и объемом, а также связана с толщиной слоя. Изучение такой зависимости имеет значение при исследовании любого материала, но особенно это важно для случая, ко- гда экспериментально выявляется нижняя размытая ступенька для угла А .

В действительности нижняя и верхняя ступеньки для поляризационного угла А в чистом виде проявляются далеко не всегда. Кратко рассмотрим такую ситуацию на примере начальной верхней ступеньки, имеющей место при малой толщине пленки и выполнении условия (12). С ростом толщины d пленки верхняя ступенька постепенно переходит в нижнюю ступеньку. Данный процесс начинается с приближением толщины d к значению, равному половине периода D ₀ поляризационных углов по толщине. В процессе перехода кривая А ( ф ₀) разделяется в точке ф₀ = ф₀p на две кривые. Левая кривая ( ф ₀ <  ф ₀ p ) — это уже нижняя ступенька, а правая кривая ( ф ₀ >  ф ₀ p ) представляет собой остаток верхней ступеньки. При этом в точке ф ₀ = ф ₀ p поляризационный угол А испытывает скачок от нуля до 360°

⁰,      ф о = ф о p ^- 0,

360 ° , ф о = ф о p + 0.

С ростом толщины d угол перехода ϕ0 p смещается к значению 90°. Период D0 зависит от угла падения ϕ0 и достигает максимального значения при ϕ0 = 90°. Процесс перехода к нижней ступеньке заканчивается, когда угол ϕ0 p и толщина пленки достигают значений ф0p = 90°, d = 2D0(90°). (17)

При дальнейшем увеличении толщины d нижняя ступенька сохраняется вплоть до того момента, когда толщина приближается к концу первого периода D ₀ . Постепенный переход толщины d через границу каждого периода D ₀ ( ϕ ₀) сопровождается аналогичным преобразованием нижней ступеньки в верхнюю. Только в этом случае точка ф ₀ = ф ₀ p разделяет кривую А ( ф ₀) на такие две части, из которых левая часть представляет собой уже верхнюю ступеньку, а правая — остаток нижней ступеньки. Соответственно формула (16) преобразуется к виду

А =

'360 ° , 0,

ф 0 = ф 0 p ^{- 0}, ф 0 = ф 0 p ⁺ 0.

При переходе толщины пленки через границу второго, третьего и более высоких порядков периодов характер преобразования ступеньки усложняется. При использовании эллипсометров с широким спектральным диапазоном описанное преобразование ступеньки для угла Δ проявляется при уменьшении длины волны даже при сравнительно небольшой толщине пленки. И если такое преобразование наблюдается в эксперименте на жидкости, то это со всей очевидностью указывает на наличие поверхностного слоя. Необходимо отметить, что если кривая Δ(ϕ0) разбивается на части, отвечающие разным типам ступенек, то коэффициент поглощения, определенный по формулам (2)–(4), не учитывающим наличия поверхностного слоя, меняет свой знак при переходе от одной части кривой к другой. Очевидно, в этом случае мы имеем дело с аналогом ω коэффициента поглощения. Как следует из формул (2) и (4), коэффициент κ , а значит, и его аналог ω пропорционален величине sinΔ . Это означает, что нет особого смысла в отдельном исследовании зависимости параметра ω от угла падения и длины волны. Достаточно исследовать зависимость поляризационного угла Δ от этих величин. Поэтому при исследовании поверхности жидкости можно не акцентировать внимание на параметре ω . Вопрос о характере преобразования кривой Δ(ϕ0) , наблюдающегося при росте толщины пленки, подробно рассмотрен в работах [6, 7].

Важно отметить, что эксперимент, проведенный на чистой воде, физиологическом растворе и на разных образцах плазмы крови с использованием спектрального эллипсометра, определяет полную или частичную верхнюю ступеньку для угла Δ . Этот факт, как и следующее из него отрицательное значение параметра ω, имеет большой физический смысл. Он со всей очевидностью указывает на наличие поверхностного слоя на однородной по составу жидкости. Поверхностный слой на образцах плазмы крови, полученных от разных больных, отличается по своим параметрам — толщине и оптическим постоянным. Это отражается на поведении измеряемых поляризационных углов Ψ и Δ , значения которых, очевидно, не зависят от выбора модели отражающей поверхности. Таким образом, и в простейшей модели однородной среды мы имеем дело с неискаженными выбором модели поляризационными углами, поведение которых указывает не только на наличие поверхностного слоя, но и на зависимость его характеристик от выраженности заболевания. В настоящей работе используется модель однородной среды. В этом случае мы имеем дело с эффективным показателем преломления nef плазмы крови, поведение которого также связано с выраженностью заболевания. Эти результаты значительно усиливаются при использовании спектрального эллипсометра с широким диапазоном спектра. Но это только первый этап работы. На втором этапе задача будет состоять в том, чтобы решить обратную задачу относительно параметров поверхностного слоя. Это значительно усилит информативность метода эллипсометрии. Обратная задача в этом случае математически некорректна, и для ее решения требуются специальные методы, а также достаточно большой набор углов падения ϕ0 с достаточно малым шагом по этому углу.

• 2.    ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ФИЗИОЛОГИЧЕСКОГО РАСТВОРА

И ПЛАЗМЫ КРОВИ

Измерения поляризационных углов Ψ и Δ проводились на спектральном эллипсометре. Спектральный эллипсометр и столик с ячейкой представлены на рис. 2. Прибор имеет спектральный диапазон

λ ∈ (250–1100) нм.          (19)

а                                      б

Рис. 2. Спектральный эллипсометр.

а — общий вид спектрального эллипсометра; б — столик с ячейкой

При измерениях могут использоваться следующие возможные для данного эллипсометра значения угла падения светового пучка:

ϕ ₀ =45, 50, 55, 60, 65 и 70°. (20)

Прежде чем перейти к результатам измерений на образцах плазмы крови, остановимся на результатах экспериментального исследования физиологического раствора.

• 2.1.    Экспериментальное исследование физиологического раствора

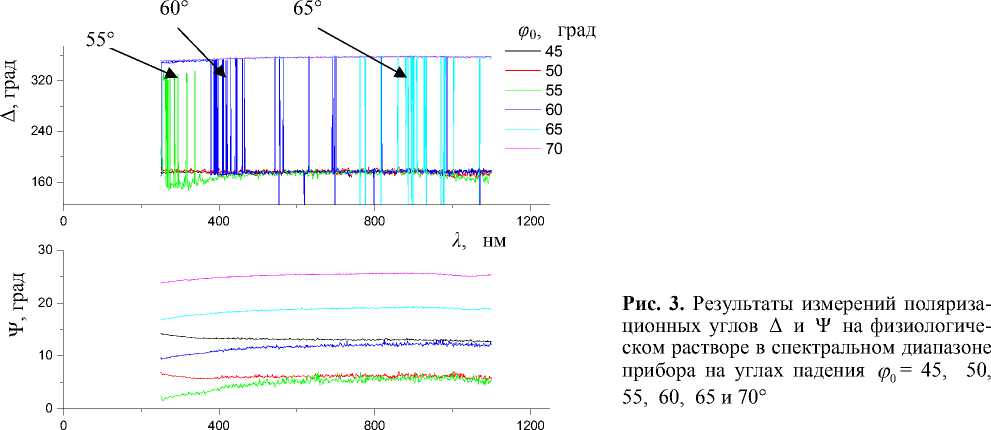
Измерения поляризационных углов Ψ и Δ для физиологического раствора проведены на всех углах падения из (20). Результаты измерений для спектрального диапазона (19) представлены на рис. 3.

Относительное расположение на данном рисунке кривых Ψ (λ) , отвечающих разным значениям угла падения ϕ0 (см. (20)), соответствует стандартной зависимости Ψ(ϕ0 ) для каждого значения длины волны λ . Что касается кривых Δ(λ) , то при углах падения 55, 60 и 65° на этих кривых наблюдаются резкие скачки. Наличие таких скачков можно объяснить не только наличием поверхностного слоя на физиологическом растворе, но и достаточно большой толщиной этого слоя. Эта толщина должна быть сравнима по порядку величины с периодом поляризационных углов по толщине слоя. Для получения более четкой картины необходимо использовать спектральный эллипсо- метр с гораздо более мелким шагом по углу падения ϕ0 по сравнению с указанным в (20). Здесь имеется в виду открывающаяся в данном случае возможность достаточно точного построения (для каждого значения длины волны) кривых

Δ ( ϕ ₀) и Ψ ( ϕ ₀) .

Большой интерес в связи с необходимостью оценки степени влияния поверхностного слоя представляет расчет оптических параметров в модели однородной среды. Как обосновано в предыдущем разделе, нет особого смысла в рассмотрении аналога ω коэффициента поглощения. Поэтому ограничимся эффективным показателем преломления n _ef .

На рис. 4 приведены кривые n _ef ( λ ) , отвечающие разным значениям угла падения ϕ ₀ (см. (20)). Из рисунка видно, что на углах падения 55, 60 и 65° параметр n _ef испытывает резкие колебания. Это находится в полном соответствии с характером кривых Δ ( λ ) на тех же углах падения. По относительному расположению кривых n _ef ( λ ) можно сделать вывод о существенной зависимости параметра n _ef от угла падения ϕ ₀ при любом заданном значении длины волны λ . Само по себе это указывает на наличие поверхностного слоя.

Таким образом, по характеру кривых Δ ( λ ), как и по существенной зависимости параметра n _ef от угла падения ϕ ₀ при любом заданном значении

λ , нм

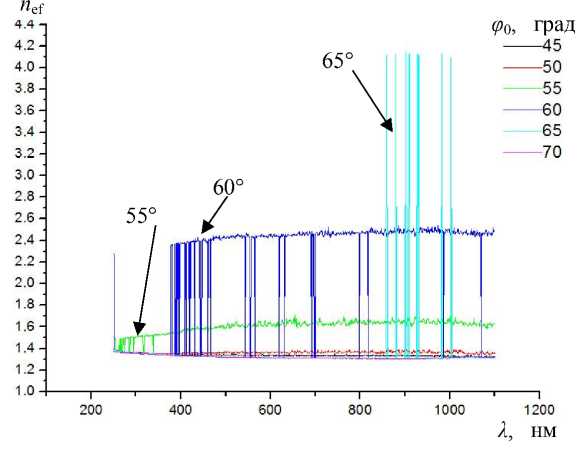
Рис. 4. Спектральная зависимость эффективного показателя преломления n _ef для физиологического

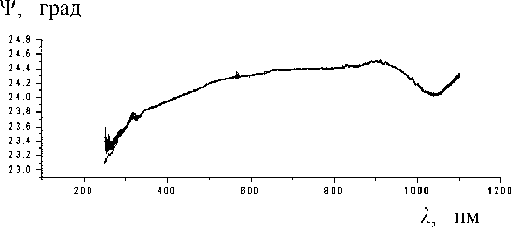
Рис. 5. Экспериментальные зависимости Ψ( λ ) на физиологическом растворе для 11 серий измерений

раствора длины волны λ , можно сделать вывод о наличии выраженного поверхностного слоя на физиологическом растворе.

Эксперимент на физиологическом растворе позволил также оценить погрешность в измерении поляризационных углов. Было проведено 11 серий измерений углов Ψ и Δ в спектральном диапазоне прибора на угле падения ϕ ₀ = 70°. Условия проведения эксперимента одинаковы. Ограничимся рассмотрением результатов измерений для угла Ψ . Экспериментальные зависимости Ψ ( λ ) для всех одиннадцати серий измерений приведены на рис. 5. Как видно из приведенных графиков, погрешность измерений очень мала. Примерно такой же результат имеет место и для угла Δ . Отсюда следует и малая погрешность в определении интегралов наполнения для углов Ψ и Δ , используемых при проведении полного факторного эксперимента на образцах плазмы крови. Данные интегралы наполнения представляют собой интегралы от поляризационных углов Ψ и Δ по d λ . Для примера приведем среднеквадратичную ошибку в определении интеграла наполнения для угла Ψ . Она составила около 0.25 %, что является довольно малой величиной.

Перейдем теперь к результатам экспериментального исследования образцов плазмы крови.

• 2.2.    Экспериментальное исследование плазмы крови больных, страдающих хроническим панкреатитом

Образцы плазмы крови больных хроническим

Табл. 1. Характеристики экспериментального массива

№ п/п, пол больного Дата Фиброз Псевдокисты Кальци-наты 1, муж 01.02.13 + + + 2, жен 06.02.13 + + + 3, муж 14.03.13 + + + 4, муж 28.05.13 + + + 5, муж 04.04.13 + + + 6, жен 10.04.13 + + + 7, муж 30.05.13 + + + 8, муж 28.05.13 + + + 9, муж 01.04.13 - - - 10, муж 04.04.13 - - - 11, муж 12.03.13 - - - 12, жен 23.05.13 - - - 13, жен 30.05.13 - - - 14, муж 16.05.13 + + - 15, муж 02.04.13 + - + 16, жен 04.04.13 + - - 17, муж 28.05.13 - + + 18, жен 26.02.13 - + - 19, муж 01.02.13 - - + панкреатитом (ХП), находящихся на лечении в 7 ГКБ г. Москвы, были получены в замороженном виде. Непосредственно перед проведением эксперимента образец подвергался разморозке при комнатной температуре в течение часа. Затем образец смешивался с необходимым количеством физиологического раствора, выливался в чашку Петри и помещался на столик эллипсометра. Через 20 мин проводились измерения.

В табл. 1 приведен список исследуемых образцов плазмы крови с указанием номера исследования и пола больных, даты проведения обследования и морфологических признаков ХП: наличие фиброза, псевдокист, кальцинатов поджелудочной железы.

В таблице больные сгруппированы по признакам проявления ХП. В первой группе (номера 1–8) объединены больные, у которых проявляются все основные признаки (фиброз, псевдокисты и каль-цинаты) ХП. В этом случае в таблице каждому признаку соответствует знак плюс. Вторую группу (группу "здоровых", номера 9–13) образуют те, у кого основные признаки ХП практически не проявляются (каждому признаку соответствует знак минус). В третью группу (номера 14–19) входят больные, у которых проявляются не все основные признаки (знаки плюс и минус чередуются). Все данные получены в период с февраля по май месяц 2013 г.

Измерения поляризационных углов Ψ и Δ проводились в спектральном диапазоне прибора на угле падения ϕ ₀ = 70°. Массив измерений поляризационных углов представлен на рис. 6 и 7. Как следует из этих рисунков, разброс углов Δ и Ψ по образцам плазмы при заданной длине волны λ составляет примерно 5 и 2° соответственно. Для эллипсометрии это большие величины, что указывает на хорошие возможности метода для диагностики хронического панкреатита у больных с различными характеристиками состояния поджелудочной железы. В связи с этим возникает также необходимость расчета оптических параметров в модели однородной среды. Как и в случае с физиологическим раствором, ограничимся рассмотрением эффективного показателя преломления n _ef . На рис. 8 приведены кривые n _ef ( λ ) , отвечающие различным образцам плазмы крови. Как и следовало ожидать, исходя из вида кривых Δ ( λ ) и Ψ ( λ ) (см. рис. 6 и 7), наблюдается существенный разброс параметра n _ef ( λ ), причем для каждого значения λ по образцам плазмы. Отметим также, что поведение кривых Δ ( λ ) явно указывает на наличие поверхностного слоя на образцах плазмы. Все значения Δ ( λ ) близки к 360°, а это, как следует из пояснений первого раздела, и указывает на

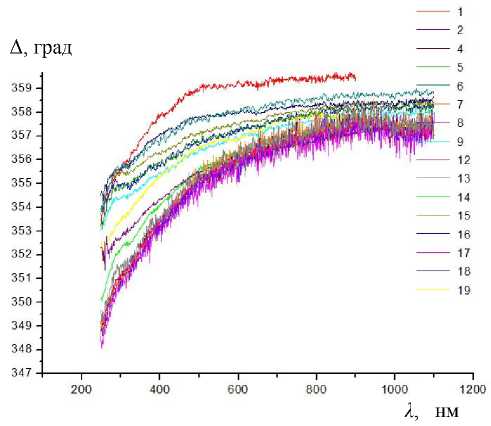
Рис. 6. Массив измерений поляризационного угла Δ на образцах плазмы крови группы больных (1–19)

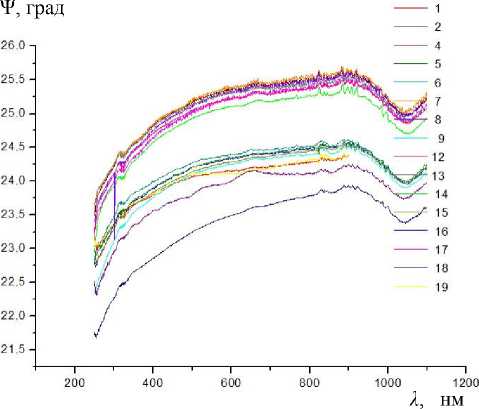
Рис. 7. Массив измерений поляризационного угла Ψ на образцах плазмы крови группы больных (1–19)

наличие поверхностного слоя. Более того, указанный выше разброс углов Δ и Ψ по образцам плазмы при заданной длине волны λ объясняется прежде всего изменением параметров поверхностного слоя. Если пренебречь данным поверхностным слоем, то разброс углов Δ и Ψ совершенно не связан с некоторым изменением показателя преломления однородного объема плазмы и весьма слабо связан с изменением коэффициента поглощения однородной плазмы. Этот вывод не вызывает сомнений еще и потому, что измерения проводились на угле падения ϕ ₀ = 70°, далеко отстоящем от угла Брюстера.

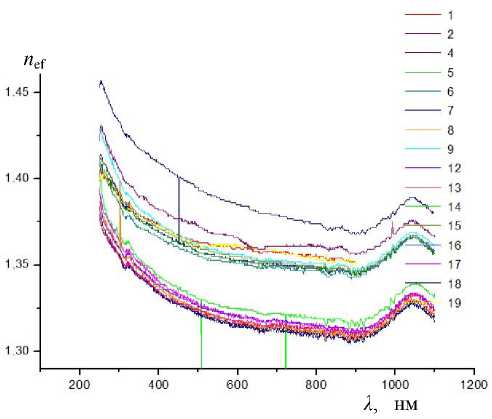
Рис. 8. Спектральные зависимости эффективного показателя преломления n _ef для образцов плазмы крови группы больных (1–19)

Таким образом, если опираться в конечном итоге на оптические постоянные однородного объема плазмы и параметры поверхностного слоя, то основными носителями информации о характере заболевания поджелудочной железы являются параметры поверхностного слоя. В настоящей работе мы используем простейшую модель однородного образца с резкой (геометрической) границей. А в этом случае к числу диагностических признаков относится не только поведение не зависящих от выбора модели отражающей поверхности поляризационных углов Δ ( λ ) и Ψ ( λ ) на некотором массиве образцов плазмы, но и связанное с ними поведение эффективного показателя преломления n _ef ( λ ) . Именно поэтому полный факторный эксперимент, которому посвящен следующий раздел, целесообразно проводить относительно функций

Ψ ( λ ), Δ ( λ ) и n ef ( λ ). (21)

• 3.    ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ НА ОБРАЗЦАХ ПЛАЗМЫ КРОВИ

Полный факторный эксперимент (ПФЭ) — это система опытов, при которой реализуются все возможные неповторяющиеся комбинации уровней факторов (см. [3, 4]). ПФЭ служит для математического описания процесса в виде отрезка ряда Тейлора. Для аддитивной математической модели используют алгебраические полиномы. Для наших целей используем неполные полиномы второй степени — нелинейность (кривизна) за счет взаимовлияния факторов X1, X2, X3

y = b 0 + b 1 X 1 + b 2 X 2 + b 3 X 3 + b 12 X 1 X 2 +

+ b 13 X 1 X 3 + b 23 X 2 X 3 + b 123 X 1 X 2 X 3 ,       (22)

где b 0 , b 1 , b 2 ,…, b 123 — коэффициенты регрессии.

Величина y, характеризующая процесс, непосредственно связана с используемым методом. Так как выбранная модель не содержит квадратов факторов, то достаточно, чтобы в опытах каждый фактор принимал только два уровня (+1 и –1). Такой ПФЭ называют экспериментом типа 2k, где k — число факторов. Для нашего случая k = 3, 2k = 8.                (23)

В качестве факторов X 1 , X 2 , X 3 рассмотрим такие признаки хронического панкреатита, как фиброз, псевдокисты и кальцинаты поджелудочной железы:

X 1 (фиброз), X 2 (псевдокисты), X 3 (кальцинаты). (24)

Проведем полный факторный эксперимент относительно параметров (21).

• 3.1.    Планирование полного факторного эксперимента для поляризационного угла Ψ

Чтобы охватить весь спектральный диапазон прибора, в качестве величины y (см. (22)) рассмотрим интеграл наполнения y =∫Ψ(λ)dλ.             (25)

Матрица планирования ПФЭ для угла Ψ имеет вид табл. 2, где y э — экспериментальное значение интеграла наполнения (25).

В первом столбце матрицы указан номер исследования, проводимого на образце плазмы крови соответствующего больного. Каждому исследованию соответствует несколько серий измерений на спектральном эллипсометре (несколько экспериментов). Ввиду высокой точности прибора вполне достаточно двух измерений для каждого исследования. При этом оба эксперимента дают практически одинаковые значения величины y э .

Далее нам понадобится построчная дисперсия, определяемая выражением [3, 4]

∑ ( yэ - y )²

Si ² = ^m            ,               (26)

f ₁

где i — номер строки (номер исследования); m — число экспериментов (на данном исследовании); f 1 = ( m – 1) — число степеней свободы.

Суммирование в (26) идет по экспериментам (на данном исследовании) от 1 до m . В качестве

Табл. 2. Матрица планирования ПФЭ для угла У

№ исследования	X 0	Х 1	Х 2	Х 3	X 1 X 2	X 1 X 3	X 2 X 3	X 1 X 2 X 3	y э
1	+	+	+	+	+	+	+	+	20464.50
2	+	+	+	-	+	-	-	-	21157.00
3	+	+	-	+	-	+	-	-	20502.00
4	+	+	-	-	-	-	+	+	20532.30
5	+	-	-	-	+	+	+	-	20448.30
6	+	-	+	+	-	-	+	-	21256.57
7	+	-	+	-	-	+	-	+	19849.10
8	+	-	-	+	+	-	-	+	20472.20
Коэффициенты регрессии
Обозначение	b 0	b 1	b 2	b 3	b 12	b 13	b 23	b 123	—
Значение	20585.25	78.7	96.55	88.57	50.25	–269.27	90.17	–255.72

параметра y , входящего в формулу (26), берется среднее значение интеграла наполнения для группы больных по всем признакам ХП ( y ₁), здоровых ( y 2 ) и физиологического раствора ( y 3 )

y 1 = 20952.865, y 2 = 21018.197, y 3 = 20639.35. (27)

Рассчитав построчные дисперсии при y = y i ( i = 1, 2, 3), находим затем расчетное значение критерия Кохрена (см. [4])

с (ZL p " Z Si

= 0.496.

Суммирование в формуле для G р идет по исследованиям (по строкам таблицы). Определим также критическое значение критерия Кохрена (см. [4]) и сравним его с расчетным значением данного критерия

G кр = 0.68 >  G р . (29)

Полученное неравенство означает, что все исследования имеют одинаковую точность.

Затем определим дисперсию S ²( y ) воспроизводимости эксперимента (параметра оптимизации) и ошибку S ( y ) (стандарт) эксперимента, используя формулу

S ²

s ²( y ) =

N

.

В формуле (30) величина N — это число исследований (по табл. 2), а суммирование, как и в формуле (28), идет по всем исследованиям (по 8 строкам в табл. 2). Эти параметры рассчитываются для каждой из величин y = y i .

Из условия ортогональности матрицы для полного факторного эксперимента следует, что дисперсии S2 (bi) и ошибки S(bi) всех коэффициентов регрессии равны между собой и определяются соотношениями s 2( b)=Z^y.,   s (b)=SM.(31)

i   Nm        i

После этого легко определяется доверительный интервал для коэффициентов регрессии

Ab=±tkp • S(b),(32)

где t кр — критическое значение критерия Стьюдента (см. [4]).

По поводу критического значения критерия Стьюдента необходимо сделать следующее пояснение. Физиологические процессы носят очень сложный характер. Их невозможно полностью описать, вводя ограниченное число параметров. Но задача состоит в том, чтобы выбранные параметры описывали изучаемый процесс, обеспечивая допустимый физиологический разброс. В нашем случае в качестве основных факторов (признаков) вполне обоснованно рассматриваются фиброз, псевдокисты и кальцинаты поджелудочной железы. Физиологический разброс для этого случая определим величиной в 20 %. Это довольно большой, но вполне допустимый разброс, позволяющий корректно описать изучаемый процесс. Доверительная вероятность в этом случае определяется величиной 0.8, а критическое значение критерия Стьюдента составляет [4]

tкр =1.4.                   (33)

Табл. 3. Матрица планирования ПФЭ для угла Δ

Коэффициенты регрессии
b 0	b 1	b 2	b 3	b 12	b 13	b 23	b 123
303420.665	264.00	–61.860	44.950	61.685	566.275	–18.025	504.30

Табл. 4. Матрица планирования ПФЭ для угла n ef

Коэффициенты регрессии
b 0	b 1	b 2	b 3	b 12	b 13	b 23	b 123
1153.945	–3.019	–3.536	–3.398	–2.026	10.117	–3.370	9.550

Рассчитав для каждой из величин y 1 , y 2 и y 3 параметр S ( y ) и связанный с ним параметр S ( b_i ) , а также учитывая (33), находим доверительный интервал для всех трех значений (27):

для y 1

Δbi= ±1.4∙195.915= ±274.281, для y2

Δ b i = ±1.4∙211.945= ±296.723, для y 3

Δ b i = ±1.4∙147.525= ±206.535.

Доверительный интервал используется для оценки статистической значимости коэффициентов регрессии уравнения. Сами же коэффициенты регрессии (b0, b1,…) находятся довольно легко. Для этого необходимо просуммировать величины yэ, взятые со знаками столбца матрицы, соответствующего определяемому коэффициенту, и разделить на число опытов N. Если коэффициент регрессии по абсолютной величине значительно меньше доверительного интервала, то он статистически незначим. Именно это и наблюдается почти для всех коэффициентов регрессии (см. табл. 2). Все коэффициенты регрессии, за исключением коэффициентов b13 и b123, значительно меньше доверительного интервала, т. е. отвечающие им в алгебраическом полиноме факторы и их сочетания статистически незначимы. Что касается коэффициентов регрессии b13 и b123, то они по порядку величины сравнимы с доверительным интервалом, поэтому отвечающие им сочетания факторов X1X3 и X1X2X3, наоборот, могут рассматриваться как статистически значимые. Это имеет место относительно каждого определенного выше доверительного интервала. Таким образом, во всех трех случаях (y = y1,2,3) реальный алгебраический полином ПФЭ для угла Ψ имеет вид y = b0 + b13X1X3 + b123X1X2X3.           (34)

Полный факторный эксперимент для остальных параметров проводится аналогично, поэтому ограничимся приведением основного результата.

• 3.2.    Планирование полного факторного эксперимента для поляризационного угла Δ

В этом случае величины y (см. (22)) определяются по интегралу наполнения y =∫Δ(λ)dλ.               (35)

Коэффициенты регрессии представлены в табл. 3.

Среднее значение интеграла наполнения для плазмы больных, здоровых и физиологического раствора, определяющее величину y из формулы (26), дается соответственно численными соотношениями y1= 303210.9, y2= 302646.87, y3= 303759.7.

Для указанных величин доверительный интервал имеет следующие значения:

для y 1

Δbi = ±1.4∙295.52 = ±413.728, для y2

Δbi = ±1.4∙395.83 = ±554.162, для y3

Δ b i = ±1.4∙310.163 = ±434.228.

Во всех трех случаях все коэффициенты регрессии ведут себя аналогично предыдущему ПФЭ для угла Ψ, т. е. реальный алгебраический полином имеет тот же вид (см. (34)).

Далее идет планирование полного факторного эксперимента по эффективному показателю преломления n _ef на всем спектральном диапазоне прибора, а также по этому же показателю, но отвечающему длине волны λ = 633 нм.

• 3.3.    Планирование полного факторного эксперимента для эффективного показателя преломления

Величины y (см. (22)) в этом случае определяются по интегралу наполнения y = Jnef(^)dA .              (36)

Коэффициенты регрессии представлены в табл. 4.

Среднее значение интеграла наполнения (35) для больных, здоровых и физиологического раствора определится величинами y1= 1144.043, y2= 1137.93, y3= 1151.997.

Для указанных значений доверительный интервал определяется соответственно численными соотношениями:

для y 1

Δbi = ±1.4∙6.52 = ±9.13, для y2

Δbi = ±1.4∙7.895 = ±11.05, для y3

Δ b i = ±1.4∙5.545 = ±7.76.

Во всех трех случаях все коэффициенты регрессии ведут себя аналогично предыдущим ПФЭ для углов Ψ и Δ, т. е. реальный алгебраический полином по-прежнему имеет вид (34).

• 3.4.    Планирование полного факторного эксперимента для эффективного показателя преломления на длине волны λ = 633 нм

Полный факторный эксперимент для эффективного показателя преломления nef на длине волны λ= 633 нм решено провести для дополнительной проверки полученных результатов. Матрица планирования полного факторного эксперимента для этого случая имеет вид табл. 5. В приведенной таблице величина yэ — это значения nef на длине волны λ = 633 нм. В качестве y (из формулы (26)) берем среднее значение показателя nef для группы больных, здоровых и физиологического раствора y1= 1.338, y2= 1.33, y3= 1.348.

Табл. 5. Матрица планирования ПФЭ для эффективного показателя преломления n _ef на длине волны λ = 633 нм

№ исследования	X 0	Х 1	Х 2	Х 3	X 1 X 2	X 1 X 3	X 2 X 3	X 1 X 2 X 3	y э
1	+	+	+	+	+	+	+	+	1.359
2	+	+	+	-	+	-	-	-	1.324
3	+	+	-	+	-	+	-	-	1.354
4	+	+	-	-	-	-	+	+	1.352
5	+	-	-	-	+	+	+	-	1.355
6	+	-	+	+	-	-	+	-	1.320
7	+	-	+	-	-	+	-	+	1.382
8	+	-	-	+	+	-	-	+	1.361
Коэффициенты регрессии
Обозначение	b 0	b 1	b 2	b 3	b 12	b 13	b 23	b 123	—
Значение	1.35	–0.0036	–0.0046	–0.0024	–0.0011	0.012	–0.0044	0.0126

Для указанных значений доверительный интервал определяется численными соотношениями:

для y 1

Δbi = ±1.4∙0.0081 = ±0.011, для y2

Δbi = ±1.4∙0.00994 = ±0.0139, для y3

Δ b i = ±1.4∙0.00674 = ±0.0094.

По сравнению с указанными доверительными интервалами все коэффициенты регрессии ведут себя так же, как и в трех предыдущих факторных экспериментах, т. е. реальный алгебраический полином имеет вид (34).

Таким образом, все рассмотренные полные факторные эксперименты приводят к одинаковым результатам, т. е. все проведенные расчеты корректны. Отметим также, что общий результат не зависит от выбора для 1-го и 5-го исследований образцов плазмы крови, отвечающих соответственно группе больных (по всем признакам ХП) и группе здоровых.

ВЫВОДЫ

• 1.    Все коэффициенты регрессии, за исключением коэффициентов b 13 и b 123 , значительно меньше доверительного интервала, т. е. отвечающие им в алгебраическом полиноме факторы и их сочетания статистически незначимы. Что касается коэффициентов регрессии b 13 и b 123 , то они по порядку величины сравнимы с доверительным интервалом, поэтому отвечающие им сочетания факторов X 1 X 3 и X 1 X 2 X 3 , наоборот, могут рассматриваться, как статистически значимые. С учетом этого реальный алгебраический полином имеет вид

• 2.    Для более надежного расчета доверительного интервала при y = y 2 (для здоровых пациентов) необходимо в полной мере обеспечить статистический подход.

• 3.    В дальнейшем необходимо провести многоугловые (по углу падения светового пучка) измерения не только для физиологического раствора, но и для цельной плазмы и ее компонентов.

• 4.    При проведении серии измерений физиологического раствора было выявлено, что ошибка измерений крайне мала и составляет около 0.25 %.

• 5.    Для повышения точности измерений также имеет смысл использовать термостатическую ячейку.

y = b ₀ + b ₁₃X₁X₃ + b ₁₂₃X₁X₂X_3.

Таким образом, наибольшее влияние на оптические параметры, определяемые с помощью метода эллипсометрии на образцах плазмы крови рассмотренной группы больных ХП, оказывает одновременное действие факторов Х 1 и Х 3 (фи броз + кальцинаты), а также одновременное действие всех трех факторов (фиброз + псевдокисты + кальцинаты). Фактически это означает, что на данной группе больных в среднем в наибольшей степени проявляются одновременное действие факторов Х 1 и Х 3 , а также одновременное действие всех трех факторов.

Учитывая полученные результаты, особенно факт значительно более выраженного одновременного действия факторов Х 1 и Х 3 , а также одновременного действия всех факторов Х 1 , Х 2 , Х 3 , целесообразно провести рассмотрение полного факторного эксперимента, используя другие физические параметры. К числу таковых можно отнести толщину и показатель преломления поверхностного слоя. Эти параметры могут сильно зависеть от типа и выраженности заболевания. С этой же целью по-прежнему можно использовать поляризационные углы и эффективный показатель преломления среды с неучтенным поверхностным слоем. На этот раз они должны рассматриваться как функции угла падения ϕ ₀ светового пучка

Ψ ( ϕ ₀) , Δ ( ϕ ₀) , n _ef( ϕ ₀)

при заданной длине волны. Однако во всех этих случаях требуется достаточно большой набор углов падения ϕ ₀ с достаточно малым шагом по этому углу.

Выражаем благодарность нашим коллегам из ИФП СО РАН С.В. Рыхлицкому и В.А. Швецу за изготовление и отладку спектрального эллипсометра, а также за консультации по данному прибору.

Работа была поддержана темой РАН "Исследование физических основ и разработка технологии элементной базы сенсорной наноэлектроники и наноструктур СВЧ и ТГц диапазонов" (номер госрегистра-ции 01201374761), а также Госконтрактом с Минобрнауки РФ № 14.427.11.0004 от 4 октября 2013 г. на НИР "Разработка конструкции и исследование характеристик экспериментальных образцов полупроводникового приемника терагерцового диапазона" (Договор от 17 октября 2013 г. № 135/135/640–13).