О выборе математических моделей кинетики культивирования дрожжей saccharomyces cerevisiae в условиях дефицита кислорода

Развитие микроорганизмов происходит под действием множества факторов, функционально связанных между собой. Установить эту связь в виде математических зависимостей (моделей) – задача сложная, интересная и необходимая. Необходимость ее решения диктуется высокими темпами развития микробиологических отраслей промышленности, возросшими требованиями к проектным работам, широкой автоматизацией технологических процессов и их оптимизации. Удовлетворить эти требования будет трудно, не имея данных по кинетике развития популяции клеток и математических моделей, адекватно отражающих течение биологических процессов. И не случайно проблеме моделирования кинетики биологических процессов уделяют большое внимание многие известные ученые [1, 2, 10].

Гипотеза о пропорциональности первой степени между приростом биомассы и ее концентрацией в культуральной среде.

Наиболее известной математической моделью кинетики развития микроорганизмов является экспоненциальная зависимость изменения концентрации клеток в культуральной жидкости во времени. Вывод модели основан на предположении о непрерывном делении клеток в неограниченном объеме, в условиях отсутствия дефицита питания и влияния отрицательных факторов, связанных с жизнедеятельностью клеток.

Согласно принятым условиям высказана гипотеза, что прирост биомассы А х за период времени Ат прямо пропорционален концентрации биомассы (клеток) в культуральной среде X и времени, т.е. А х = ц х Ат [1,2]. В дифференциальной форме это равенство имеет вид уравнения (1):

d x d т

ц х ,

где коэффициент пропорциональности ц носит название локальной удельной скорости прироста биомассы. После интегрирования уравнения (1) в пределах от х ,- до x _J+1 и от т i до т i _{+ 1} получим:

ц(т,,1 -т,-)

X + 1 = x i e   ^{+ 1}     .          (2)

Кроме локальной удельной скорости, пользуются еще величиной средней удельной скорости ц определяемой в промежутке времени от т_; = 0 до произвольного значения т и от x = х_н до x , в таком случае из уравнения (2) следует [2]

X = Х_н е ^цт .                (3)

Чтобы при обработке опытных данных не быть зависимыми от размерностей, концентрации в культуральной жидкости в дальнейшем будем выражать в безразмерном виде, как отношение текущих концентраций к начальным: х_ь = х / х _н. В новой записи уравнение (3) примет вид:

X b = е ^^т. (4)

В конечном итоге, при переводе безразмерных величин в размерные, величина текущих значений концентраций биомассы будет зависеть от выбора размерности их начальных значений.

Уравнения (3) и (4) выражают закон экспоненциального развития микроорганизмов. Дальнейшая задача заключается в установлении зависимости удельной скорости ц от тех или иных факторов, например, температуры, pH среды, начальной концентрации микроорганизмов и субстрата; гидродинамических условий в культиваторе, последние в свою очередь зависит от интенсивности перемешивания культуральной среды, и т.п.

Обычно считается, что отклонение от экспоненциального закона говорит о несоблюдении ранее принятых условий. Удельную скорость роста при том или ином лимитирующем факторе выражают в виде различных зависимостей. В данной статье не ставится задача их анализа, а желающим детально разобраться в их сути, рекомендуем обратиться к литературе [1–5].

Гипотеза о степенной зависимости прироста биомассы от ее концентрации в культуральной среде.

Можно привести много случаев, когда развитие микроорганизмов не подчиняется экспоненциальной зависимости и условие (1) не всегда соблюдается. Более верным было бы предположение - Δ x ~. x ^m . Примером тому может быть развитие дрожжей Saccharomyces cerevisiae при наличии лаг-фазы, дефиците кислорода, когда принудительная подача воздуха в культуральную среду отсутствует, и кислород проникает в жидкость за счет молекулярной диффузии через ее свободную поверхность и т.п. Другим примером может служить культивирование гриба Medusomyces gisevi и др. [6–8]. Учитывая сказанное, более правильным будет записать дифференциальное уравнение (1) в ином виде:

dx = kx”. (5) dт

В уравнении (5) коэффициент k аналогичен удельной скорости μ в уравнении (1). В частном случае показатель степени m может равняться и единице. При m = 1 k = μ и в итоге получим уравнение экспоненты. Таким образом, уравнение (1) является частным случаем уравнения (5).

Интегрируя уравнения (5) в тех же пределах, что и уравнение (1), после приведения конечного выражения к безразмерному виду, получим уравнение степенного вида:

x 1 - m = 1 + (I ^{- m} ) k _T ^.

b             1-m xн

Обозначив в правой части равенства (6) отношение параметров перед τ через δ и проведя несложные преобразования, запишем:

xb = (1+бт)1 - m.

Уравнение (7) можно привести к несколько иному виду:

xb = (1+5т) m1, где             mi = —1—.(9)

1 — m

В уравнении (8) параметр 5 аналогичен ц в уравнении (3) и представляет собой среднею относительную удельную скорость прироста биомассы.

Интерес представляет анализ уравнения (9). Ранее уже было сказано, что при m = 1, интегрирование уравнения (5) дает экспоненциальную зависимость (4). При подстановке в уравнение (9) m = 1, функция m 1 ( m ) претерпевает разрыв и m 1 = ± ∞. Именно в зоне разрыва имеет место экспоненциальная зависимость (4). При m < 1, m 1 всегда будет больше нуля, и мы получим уравнение степенного вида (8).

При m > 1, m1 будет иметь отрицательное значение, и мы получим уравнение иного вида:

S_h =--- ¹—

(1 + § , т) m ¹ '

.

В данном случае Sb обозначает любой компонент культуральной жидкости, концен- трация которого снижается при протекании биологического процесса.

Уравнения, полученные на основе гипотезы степенного вида, требуют экспериментальной проверки. В дальнейшем будет показано, что область применения уравнений вида (8) и (10) ограничена определенными условиями. Как показали исследования по культивированию дрожжей Saccharomyces cerevisiae, уравнения типа (8) достаточно точно отражают характер накопления биомассы (рисунок 1). Однако уравнение (11), полученное на основе той же гипотезы (5), такой же достаточностью не обладает при описании опытных данных по кинетике потребления субстрата (рисунок 1а), поэтому для этой цели необходим поиск другой модели.

Эмпирическая степенная зависимость.

Уравнение степенного вида, несколько иного вида, чем (8) и (10), можно получить, основываясь не на гипотезе (5), а, скорее, из соображений логики, опираясь на экспериментальные результаты. Согласно графикам x = f ( т ) (рисунок 1), мы в праве в любой момент времени концентрацию биомассы в культуральной среде выразить в виде суммы:

x = x + A x ,            (11)

н где ∆x – прирост биомассы в промежутке времени от τ = 0 до τ = τi, в общем случае изменяющейся во времени. Можно записать, что ∆x ~ τn. Тогда, с учетом этой пропорциональности, уравнение (11) примет вид:

x = x + k т ,           (12)

н1, где k1 – коэффициент пропорциональности.

Разделив обе части равенства (12) на x н и обозначив отношение k I x_H = у n , из уравнения (12) получим:

x_b = 1 + ( YT ) n ,               (13)

где Y и n - параметры, определяемые экспери- ментально. Показатель степени в уравнении (13) может иметь как положительное, так и отрицательное значение. В последнем случае уравнение (14) примет вид:

S, =----- ¹

b 1 + ( y s т ) n ^S

.

Таким образом, мы вместо уравнений (8) и (10) получили уравнения (13) и (14). Преимущество уравнений (13) и (14) перед уравнениями (8) и (10) заключается в том, что входящим в уравнение (13) и (14) параметрам проще придать вполне определенный физико-биологический смысл. Если в указанных уравнениях параметры m 1 и n имеют один и тот же смысл - темп изменения функции х ь (т) или S_b ( т ) , т.е. изменение скорости протекания биологического процессы во времени, то с параметрами δ и δ S дело обстоит сложнее. В отличие от δ в уравнении (8), из уравнения (13) легко доказывается, что величина т_и = VY есть время удвоения функции x ( т ) , а из уравнении (14) - т₅ = 1/ y_s есть время снижения функции S_b ( т ) в два раза.

Время удвоения называют еще генерацией клеток. За все время культивирования дрожжей может быть несколько генераций, причем время генерации остается постоянной. Время генерации является важной характеристикой штамма дрожжей и используется в технологических расчетах.

Экспериментальное определение эмпирических коэффициентов

Прирост биомассы. Предметом исследований являлись дрожжи Saccharomyces cerevisiae штамма Л-12. Опыты проведены на мелассных растворах с начальным содержанием сахаров в культуральной среде S = 0,115; S =0,0575 и S =0.0383, в массовых долях. Растворы приготовлялись из мелассы с известным содержанием общих сахаров. Для получения необходимой концентрации сахаров в культуральной жидкости мелассу разбавляли водой. Засевная культура приготовлялась из прессованных дрожжей 75 % влажности. Для каждого начального значения субстрата было предусмотрено четыре значения начальной концентрации дрожжей в культуральной среде: x = 3,7; 10; 30; 50 кг/м³.

Культивирование проводилось в прозрачном стеклянном сосуде в течение 6-8 ч при температуре 30-31 ^°С при pH среды 4,2-4,6. Считалось, что изменение температуры и кислотности культуральной жидкости в указанных пределах не влияло существенным образом на процесс культивирования. Через каждый час отбирались пробы для определения общей концентрации дрожжей x – кг/м³ при 75 % влажности. Визуальные наблюдения показали, что большая часть дрожжей находилась во взвешенном состоянии и лишь незначительная – оседала на дно сосуда.

Результаты экспериментальных исследований и обработки опытных данных представлены на рисунке 1 в виде графиков зависимости x _b ( т ) при . Для других значений S _H графики выглядят аналогичным образом. Для сравнительной оценки уравнений (8) и (13), обработка экспериментальных даны, с целью нахождения значений коэффициентов δ, m 1 , γ и n , велась для обоих вариантов. Для облегчения работы, предварительный выбор уравнений для расчета коэффициентов производился с помощью компьютерных прграмм CurveExpert и MatchCad [9].

На основе опытных данных установлено, что входящие в уравнения (8) и (13) параметры, связаны сложными функциональными зависимостями с начальными значениями концентрации дрожжей и углеводов в культуральной жидкости.

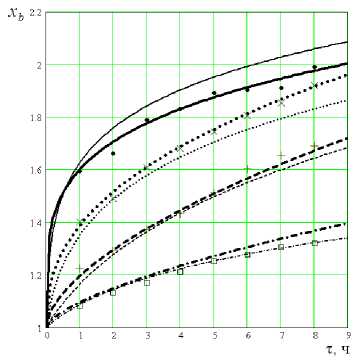
Рисунок 1. Изменение концентрации: биомассы во времени; тонкие линии соответствуют уравнению (8), толстые – (14) при S = 0,115; x = 3,7 ▬; x =10 •••; нн              н

x =30 ▬ ▬; x = 50▬ • ▬.кг/м3; знакисоответствуют опытным данным.

Поиск математических моделей начнем с анализа возможности использования уравнения (8) в качестве головного. Из нескольких уравнений, предложенных программой CurveExpert для расчета величин δ и m1, при различных значениях x были выбраны следующие:

5 = к

b

a

V хн У

(8,а)

⁽ x н b l)

m^ = a^e   ² c     .              (8,б)

Проанализируем полученные равенства. Прежде всего, отметим, что показатели степеней должны быть безразмерны. Значит безраз- мерными должны быть величины b , m и a , а коэффициенты a , b и c иметь размерность туже, что и x – кг/м3; так как при проведении экспериментов мы измеряли время в часах, то коэффициент k = 1, корректирующий размерность, имеет размерность, что δ – 1/ч.

Все указанные коэффициенты и показатели степеней в уравнениях (8,а) и (8,б) зависят от начальной концентрации углеводов в культуральной среде. Для их расчета на основе опытов выбирались соответствующие уравнения согласно требованиям, сформулированным выше. В результате, для расчета коэффициентов, входящих в уравнения (8а) и (8б), были выбраны следующие уравнения:

-( S н )

a = 1,62 S_h ^{V 0,086 У} ;             (8,в)

b = 0,0133 • 0,85 S ^н S 295 .       (8,г)

н

Проанализируем уравнения (8,в) и (8,г). Согласно рисунку 2а функция (8,в) имеет максимум Sн = 0,35. Далее, при 5 ^ 1, функция бун дет стремиться к нулю, что вполне логично. Возможно, значение Sн = 0,35 и соответствует тому предельному значению концентрации углеводов, при котором развитие дрожжей начинает тормозиться (требует экспериментальной проверки). При 5 ^ 0, а ^ 0, и согласно урав-н нению (8) 5 ^ 0, т.е. при отсутствии углеводов прироста биомассы, естественно, не будет.

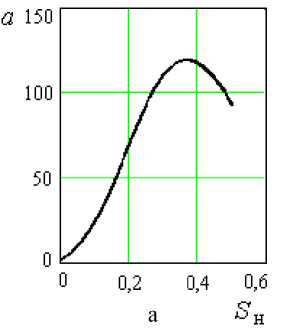
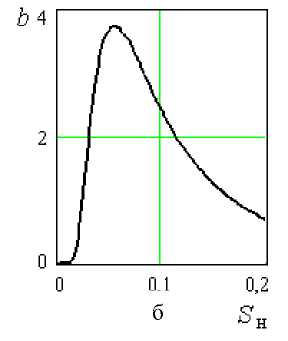
Рисунок 2. Зависимость коэффициентов a и b от S н в уравнениях (8,в) и (8,г)

Функция (8,г) при S н = 0,058 имеет максимум, следовательно и δ будет максимальным. Далее при 5 ^ 1 b ^ 0 (рисунок 2б) 5 ^ 1 . н

Таким образом влияние начального содержания углеводов S н на величину δ, выраженное уравнениями (8,в) и (8,г), не противоречит реальным условиям развития клеточной популяции и они могут быть использованы в дальнейшем при составлении математической исследуемого биологического процесса.

Недостаток функций типа (8,в) и (8,г) заключается в том, что аргумент функции входит в показатель степени, поэтому численные коэффициенты 0,086 и 1 должны иметь туже размерность, что и хн. Придать им какой-либо физико-биолгический смысл в таких уравнениях довольно сложно.

В уравнении (8,б) коэффициент a 1 определяет максимум значения функции m 1 ( х н ), а коэффициент b 1 - значение x_H = х_{т н}, соответствующее этому максимуму. С понижением начального содержания углеводов максимум темпа прироста биомассы возрастает. В тоже время он смещается в сторону увеличения x . В этой связи можно рекомендовать изменение начального засева x от 5 до 40 при отсутствии аэрации. При наличии принудительной аэрации культивирование можно проводить и при значительно более высоких значениях x [8, 9].

Для вычисления коэффициентов, входящих в уравнение (8,б) получены следующие эмпирические выражения:

_( 0,015 )

I а1 = 0,175 • 5н 1н j;        (8,д)

b 1 = 17,57 + 94,46 5 _н.      (8,е)

Таким образом, получена система уравнений (8), (8,а)-(8,е), которую можно принять за математическую модель, так как она достаточно точно, согласно рисунку 1, описывает кинетику протекания процесса культивирования дрожжей, и позволяет прогнозировать течение процесса за пределами условий эксперимента в диапазоне изменения x от 1 до 50 и S от 0, 005 до 0,3. _{н                       н},             ,

Обратимся теперь к уравнению (13). На основе экспериментальных данных была установлена линейная зависимость γ от x : н

Y = а 2 - Ь 2 • х н .            (13,а)

Установлено, что в уравнении (13,а) b = 0,00186 м³/кк • ч независимо от значения S . Для расчета коэффициента a получено эмпирическое уравнение, устанавливающее его зависимость от начальной концентрации углеводов: 1

а ₂ = 0,1028 • 0,983 ⁵ н • 5 _н ^0,14 .   (13,б)

Согласно равенству (13,б), в пределах изменения S от 0 до 0, 0013, можно принять а ₂ = 0 и y = 0 . В таком случае прирост биомассы при 5 _н<  0,0013 не происходит.

Таким образом, уравнения (13,а) и (13,б) устанавливают сложную функциональную связь удельной относительной скорости прироста биомассы с начальными значениями концентрации биомассы и углеводов в культуральной жидкости.

Для расчета темпа прироста биомассы n выбраны следующие уравнения:

• a, • x

n =----—;

8,25 + x

н

(13,в)

(13,г)

a ₃

0,428

0,06

Сравнивая модели уравнений (8) и (13),