О выборе оптимальных параметров для измерения времени задержки на основе эффекта Хонга–О–Манделя

Эффект Хонга-Оу-Манделя – один из базовых эффектов квантовой оптики – заключается в том, что если на светоделитель по разным входным каналам одновременно поступает по одному фотону, которые не будут различаться по частоте, времени прихода и направлению поляризации, то на выходе из светоделителя фотоны сгруппируются: два фотона будут наблюдаться только либо в одном, либо в другом из выходов [1] Этот эффект также получил название «антикорреляция фотонов», и данный эффект объясняется интерференцией двухфотонного излучения четвертого по полю порядка1. Если же параметры фотонов различаются существенно (по сравнению с обратной шириной спектра), то сигнал, вызванный регистрацией одиночных фотонов, будет наблюдаться также и в обоих выходах одновременно. На рис. 1, а приведена типичная схема интерферометра Хонга-Оу-Манделя (ХОМ): пары фотонов (сигнальный и холостой), образующиеся в ходе спонтанного параметрического рассеяния света (СПР) на нелинейном кристалле, направляются на разные входы светоделителя, а затем – в однофотонные детекторы, с которых в счет- чик совпадений направляются сигналы о регистрации фотонов. Типичный вид сигнала с датчика совпадений Rc(τ) приведен на рис. 1, б: в случае τ = 0 наблюдается минимум [1], вызванный эффектом антикорреляции фотонов. Зависимость Rc(τ) характеризуют с помощью величины видно-сти α = (Rсmax – Rсmin) / (Rсmax + Rсmin). В случае полной неразличимости фотонов в холостом и сигнальном канале видность α равна 1.

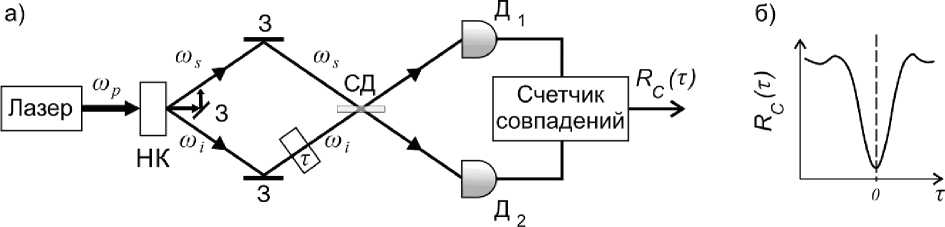
Рис. 1. a) Оптическая схема ХОМ интерферометра: ωp – частота фотона накачки; НК – нелинейный кристалл; З – зеркало; ωi, ωs – частоты холостого и сигнального фотонов; τ – временная задержка; СД – светоделитель; Д1, Д2 – детекторы; Rc(τ) – сигнал с датчика совпадений; б) Типичный вид зависимости сигнала с датчика совпадений от величины времени задержки τ

Изменение величины τ вследствие действия каких-либо факторов приводит к изменению сигнала с датчика совпадений: данное обстоятельство можно использовать в метрологии для построения измерительных приборов, основанных на оценке величины τ на основе данных с датчика совпадений [2].

Отметим, что данный подход обладает рядом преимуществ. В отличие от классической интерферометрии, ХОМ-интерференция не зависит от изменения оптической фазы: ХОМ-интерферометр сохраняет свою способность измерять временные задержки, даже когда флуктуации разности хода составляют порядка длины волны и более. Типичные фазозависимые методы чувствительны к фазовым флуктуациям, тогда как ХОМ-интерферометрия невосприимчива к изменениям относительной фазы между двумя фотонами. Датчик на основе ХОМ-эффекта не требует потенциально непрактичных и/или сложных систем стабилизации, как это обычно требуется в классической интерферометрии. Эти особенности ХОМ-эффекта привели к предложениям для датчиков задержки времени со сверхвысоким временным разрешением [3].

Данная работа посвящена изучению абсолютной погрешности измерения времени задержки на основе ХОМ-интерферометра с входным бифотонным состоянием света. Учет коррелированных членов с большим числом фотонов [4] может внести дополнительные изменения в оценку погрешности временной задержки. Также на точность оценки временной задержки может оказывать влияние возможная запутанность генерируемых фотонов с фотонами накачки [5] в случае достаточно большой входной интенсивности света.

Оценка точности временной задержки

Бифотонное состояние неколлинеарного невырожденного по частоте светового поля в фиксированных поляризационно-пространственных модах синхронизмом типа II в частотном представлении описывается следующей волновой функцией [6]:

I ^> = ft d ^ s d ^ i f^{( a} s ^{, a} i) a + ^{( a} s ) a 2 ^{( a} i ) I °° ) , (1) где нижние индексы отвечают за сигнальную ( s ) и холостую ( i ) компоненты, выражения a + ( a s ) и a + ( a i ) описывают действие операторов рождения на соответствующих частотах на вакуумное состояние. Отметим, что спектральная амплитуда f ( a s , a i ) является нормированной функцией, то есть подчиняется условию нормировки JJ | f ( a s , a i ) | ² d a s d a i = 1.

Холостой фотон испытывает временную задержку τ , что в спектральном разложении приводит к появлению фазового множителя exp( i a i T ) в волновой функции бифотона. В данном случае временная задержка τ отсчитывается от минимума функции, показанной на рис. 1, б ( τ = 0 соответствует минимуму). Дальнейшая эволюция бифотона связана со смешением фотонов на равно-

Куц Д.А., Подошведов М.С., Воронцов А.Г.,                  О выборе оптимальных параметров

Кулик С.П., Подошведов С.А.                               для измерения времени задержки … весном светоделителе, что ведет к появлению состояния, уже напрямую связанного с ХОМ-эффектом

• 1    ^(т)> = 2 JIdmsdmi (f(MsMi)exP(Мт) -f(oi Ms)exP(^Г))a1+ (Ms)a + (®,) 1 00> .

В данном измерении число совпадающих фотоотсчетов

S = JJ d® do2 q) | m XmI 02 I,(4)

является наблюдаемой величиной, среднее значение (S> которой зависит от т. Измерение опе ратора совпадений (4) позволяет оценить значение переменной т. Точность этого измерения можно оценить с помощью формулы распространения ошибки [7]:

^А S

* = ^{,                                   (5)}

где числитель A S = ^( S ² > —( S > ² - среднеквадратичное отклонение в совпадениях фотоотсчетов, а знаменатель – величина, определяющая чувствительность среднего значения оператора S по отношению к переменной т .

В реальном эксперименте присутствуют факторы, которые могут ухудшить видность интерференционной картины. В нашем рассмотрении вклад несовершенства настройки оптической схемы может быть промодулирован посредством рассмотрения уже несбалансированного светоделителя, на котором смешиваются фотоны, что позволяет рассчитать среднее значение оператора (4) как

( S > = 1 ( 1 — ^а П d ® d M 2 I f ( М ’ ® 2 )| ² cos ( M l — MT ) ) ,                  (6)

где a - видность интерференционной картины, и здесь мы также приняли во внимание симметричность амплитуды бифотона к перестановке частот, то есть выполнение условия f (0)1,02) = f (02.0)1). Если аппроксимировать спектральную амплитуду бифотонного поля бига- уссовской функцией f (M.®?)

exp лЛМкю

^{( o} 0 ^— ® 2 )  _PYn ( О ⁺ ® 2 ^— ® 0 )

expо----

I   2( A o ) ² J ^      2( M ) ²    J

то среднее значение оператора (6) преобразуется в финальное выражение

< S > = ₅ 1 ^— exp

—

( А ® ) 2 т ² 1

где Ao - ширина спектра бифотонного поля, M - ширина условного частотного распределения, связанная с шириной спектра накачки, несущая частота которой о0 . Если мы воспользуемся соотношением (S2 > = (S>2, то по формуле распространения ошибки в уравнении (5) получим оценку ошибки неизвестной временной задержки

4 <  S > (1 — <  S > )

1 — a ² exp

^Л   ( А о ) ² т ² "

—

S

= 2

a ( A o ) ² T exp

( А о ) ² т ² '

Полученная зависимость (9) в данной работе является основой для подбора значений величин α , Δ ω при реализации в эксперименте. На рис. 2 приведены результаты численных расчетов определения времен задержки, соответствующих минимальным значениям абсолютной погрешности при заданных величинах ширины спектра бифотона, видности. Из приведенных на рис. 2 зависимостей можно видеть, что при видности больше 0,5 точка, соответствующая минимуму абсолютной погрешности времени задержки, лежит ниже точки перегиба функции ( S ( т ) > .

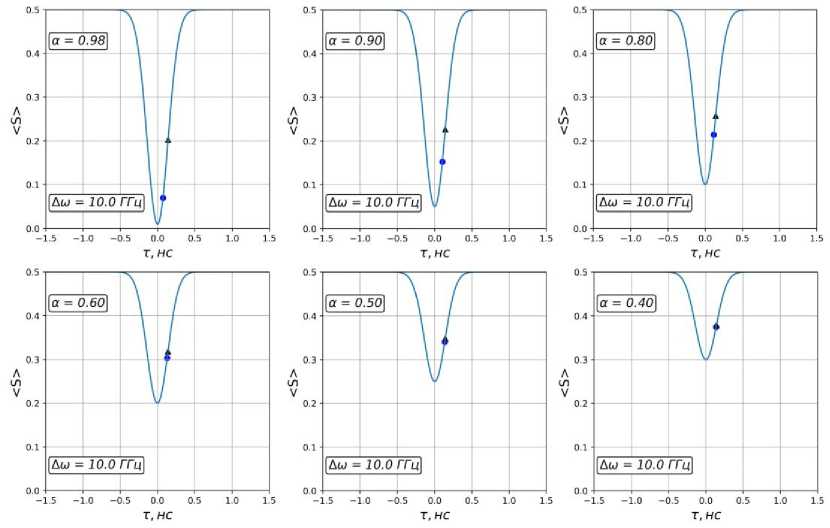
Рис. 2. Кривая (S(т)) при различных значениях видности. Круг соответствует величине т с минималь ным значением абсолютной погрешности. Треугольник - точка перегиба функции (S (т))

Выводы

В случае СПР второго типа погрешность δ τ определения времени задержки между прибытиями фотонов на светоделитель в ХОМ-интерферометре была выражена через величину ширины спектра бифотона Δ ω , видность α , а также время задержки между фотонами τ . Выражение для величины δ τ ( α , Δ ω , τ ) было получено на основе формулы распространения ошибки. Для различных значений Δ ω и α были определены такие времена задержки между фотонами τ min , для которых реализуются наименьшие абсолютные погрешности δ τ при фиксированных Δ ω и α . Было обнаружено, что при фиксированном значении Δ ω величина τ _min при уменьшении видности приближается к точке перегиба зависимости числа совпадений от времени задержки τ . Это обстоятельство нужно учитывать при проектировании работающих на основе ХОМ-интерферометра измерительных средств.

Исследование выполнено за счет гранта Российского научного фонда № 24-22-20063,