О вычислении вершины многогранника допустимых решений системы линейных ограничений

Задача нахождения вершины многогранника, задаваемого системой линейных неравенств и уравнений, встречается во всех областях, использующих линейное программирование (ЛП) в качестве основной оптимизационной модели. Так, симплекс-метод [1] для своей работы требует некоторую стартовую вершину многогранника допустимых решений. Проекционный алгоритм AlEM решения задачи ЛП, предложенный в недавней работе [2] , также требует в качестве стартовой точки вершину многогранника допустимых решений. Стартовая вершина также необходима в алгоритмах перечисления всех вершин многогранника (см., например, [3, 4] ), используемых в таких областях, как теория игр, исследование операций, математическая биология и кристаллография.

Рассмотрим систему линейных ограничений стандартного вид а1

A\bfitx \leqslant \bfitb,

где ж = (x i ,..., x n ) G K n — вектор переменных, A — вещественная матрица размера m х n, \bfitb — столбец вещественных чисел размера m. Необходимо найти вершину многогранника M \subset \BbbR ⁿ , представляющего собой область допустимых решений системы (1) . Предполагается, что многогранник M является ограниченным множеством. Наиболее известными методами вычисления вершины многогранника M являются симплекс-метод и метод исключения переменных Фурье—Моцкина.

Идея подхода, основанного на симплекс-методе, заключается в следующем [5] . Переупорядочив строки системы (1) , представим ее в виде

A ⁺ \bfitx \leqslant \bfitb ⁺

I A х ^ b , где b+ ^ 0, b > 0. Рассмотрим задачу ЛП следующего вида2:

max {( 1 , A + х — z ) | z ^ 0; A + х <  b ; A х — z <  b } ,

где z = (z i ,..., z n ) G K n — новый вектор переменных, и 1 = (1,... 1) G K n — вектор единиц. В этом случае х = 0 и z = 0 задают вершину многогранника допустимых решений задачи (2) . Таким образом, мы можем решить задачу (2) с помощью симплекс-метода. Если максимальное значение задачи (2) равно ( 1 , b } , и достигается в вершине (х * , у * ), то \bfitx ^\ast будет вершиной многогранника M , представляющего область допустимых решений системы (1) . Если максимальное значение задачи (2) меньше \langle 1 , \bfitb \rangle , то система (1) не имеет решений. Главным недостатком этого подхода является то, симплекс-метод в общем случае может потребовать экспоненциальное число шагов для получения решения [6] .

Метод Фурье—Моцкина [7] основан на решении системы линейных неравенств путем последовательного исключения переменных подобно тому, как это делается при решении системы линейных уравнений. Впервые метод исключения переменных применительно к линейным неравенствам был упомянут Фурье в 1827 году (см. [8] ). Моцкин повторно открыл и использовал этот метод в своей докторской диссертации [9] . Следуя [5] , рассмотрим метод Фурье—Моцкина применительно к задаче вычисления вершины многогранника допустимых решений системы (1) . Обозначим a _i ^j — j-тый элемент i-той строки матрицы A. Путем умножения неравенств на соответствующие положительные числа, приведем систему (1) к виду

{ x i + ( а + , х ' ) <  b + (i = 1,..., m ' )

—x i + ( а - , х ' ) <  b i (i = m ' + 1,...,m '' )                          (3)

(ai, х') < bi (i = m" + 1,...,m), где ai  = (.ai/ai>--4ai/ai\ ^i = (-ai/ai,---, —an/ai) a0 = (a2,..., an), b+ = bi/a1, bi = -bi/a1 ж' = (x2,... ,Xn). Поскольку первые две строки системы (3) равносильны условию max     ((а-, ж') — bi) < xi < min (1+ — a+, ж')) ,                 (4)

iin{m\prime+1,...,m\prime\prime}                                                               iin{1,...,m\prime} переменная x1 может быть исключена. Это позволяет перейти к следующей эквивалентной системе:

^(a i ^{, ж} ' ⁾ — b i <  b + ^- (^{a + , ж} ' ⁾

( a _i ^{, ж} ' ⁾— bi <  b m , — ^{( a} m , ^{, ж} ' ⁾

(a", ж') < bi которая равносильна системе

(i = m ' + 1,..., m ' )

(i = m ' + 1,..., m " )

(i = m " + 1,... ,m),

^(a~ i + ^a + , ж ' ) <  b + + b i

( i

= m ' + 1,..., m '' )

( ai + a m , , ж ' ) <  b m, + b i _ч ( a ^ ж ' ) <  b i

(i = m ' + 1,..., m '' )

(i = m '' + 1,... ,m).

Эта система включает в себя m'(m " — m ' ) + m — m '' ограничений и n — 1 переменных. В действительности, система (5) определяет проекцию многогранника допустимых решений M исходной системы (1) на гиперплоскость x i = 0. Проекция многогранника является многогранником. Обозначим получившийся многогранник через M 1 . Если размерность многогранника M равна n, то размерность многогранника M i будет равна n — 1:

dim(M i ) = n — 1.

Продолжая процесс исключения переменных выше описанным способом, в итоге получим многогранник M n - 1 размерности 1, являющийся проекцией многогранника M n - 2 на гиперплоскость x n = 0 и представляющий собой отрезок. Очевидно, что в любой точке этого отрезка переменные x 1 , . . . , x _n- 1 принимают значение 0, а значения переменной x _n ограничиваются условием

\beta- \leqslant xn \leqslant \beta+, где \beta- , \beta+ — скалярные величины, вычисленные в ходе исключения переменных. При этом вершинам многогранника Mn-1 соответствуют минимальное и максимальное допустимые значения переменной xn. Для определенности положим хП = 0+ — n-ная координата вершины многогранника. Двигаясь в обратном порядке, вычислим остальные координаты искомой вершины, используя ограничения вида (4). Например, если мы уже нашли координаты x\ast2, . . . , x\astn, подставив их в правую часть (4) в качестве \bfitx\prime, получим х1 = fmin АА — (aA (^..., хПУ)).

i \in\{ 1,...,m ^prime \}

Таким образом мы вычислим вершину ж * = (х * , ...,хП) многогранника допустимых решений M для исходной системы ограничений (1) . Описанный метод имеет тот же недостаток, что и симплекс-метод: в общем случае метод исключения Фурье—Моцкина характеризуется экспоненциальной временной сложностью [10] .

В этой статье мы предлагаем новый метод вычисления вершины многогранника допустимых решений системы линейных неравенств, который позволяет вычислить вершину не более, чем за n итераций, где n — размерность пространства. Проекционный алгоритм, реализующий этот метод, получил название VeSP (Vertex Seeking by Projecting). Статья организована следующим образом. Раздел 1 содержит обозначения, определения и утверждения, необходимые для описания алгоритма VeSP и его численной реализации. В разделе 2 дается формализованное описание алгоритма VeSP, и доказывается утверждение о сходимости этого алгоритма. В разделе 3 представлены информация о программной реализации алгоритма VeSP и результаты вычислительных экспериментов. В заключении суммируются полученные результаты и намечаются направления дальнейших исследований. В конце статьи приводится сводка используемых математических обозначений.

1.    Определения и обозначения

В этом разделе приводятся основные определения и обозначения, используемые для описания алгоритма VeSP.

В евклидовом пространстве \BbbR ⁿ рассматривается система линейных ограничений общего вида, включающая в себя m линейных неравенств и k линейных уравнений:

A x <  b ;

_ _ Ax = b, где A G Rmxn, A G Rkxn, b G Rm и b G Rk. Предполагается, что размерность пространства n > 1, количество уравнений к ^ 0. Матрицу A будем называть граничной, а матрицу A — опорной. Предполагается, что система (6) включает в себя также неравенства вида

-x 1 <  0;

— x n <  0.

Таким образом, число неравенств m не может быть меньше размерности пространства n:

m \geqslant n.

Из (7) и (8) следует

rank (A) = n.

Подсистема

^            Z4

A\bfitx \leqslant \bfitb задает m замкнутых полупространств3

P 1 = { x G R n |( a 1 , x ) <  b i } ;

P m = { x G R n^m , x ) <  b m } .

Здесь a i ,..., a m обозначают строки матрицы A; b 1 ,... ,b m — элементы столбца b. Пересечение полупространств (10) образует замкнутый выпуклый многогранник Md , называемый граничным:

m

М = П P i .                               (11)

i=1

Полупространства (10) ограничиваются гиперплоскостями, называемыми граничными:

HI 1 = { ж G R n |( a ₁ , ж ) = b ₁ } ; ........................... (12)

^H m = ^{ Ж E M |(^a m , ^ж) = b m } .

Без ограничения общности мы можем предполагать, что среди граничных гиперплоскостей нет совпадающих.

Подсистема

Аж = b задает k гиперплоскостей, называемых опорными:

H m+1 = { ж G R ⁿ |( a m₊1 , ж ) = b m+1 } ; ................................. (13)

^H m+k = ^{{ж G M} \{ ^a m+k , ^ж) = b m+k ^} •

Здесь a m+1 ,..., a m+k обозначают строки матрицы A; b m+1 ,..., b m+k — элементы столбца b.

Пересечение опорных гиперплоскостей образует опорное подпространство S:

k _

П Hm+i , i=1

\BbbR ⁿ ,

если к >  0;

(14) если k = 0.

Область допустимых решений, определяемая системой ограничений (6) , представляет собой замкнутый выпуклый многогранник M , называемый допустимым:

M = S П MI.(15)

В частности, из (15) следуют

M C S;

M C MI.(17)

Мы будем предполагать, что допустимый многогранник M является непустым ограниченным множеством.

Обозначим через I множество индексов строк граничной матрицы А, и через I — множество индексов строк опорной матрицы A :

I = ^{ l,...,m ^} ;                                        ⁽¹⁸⁾

I = {m + 1,... ,m + к}.                                (19)

В соответствии с (19) формулу (14) можно переписать в виде

_

S =

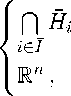
_ если I = 0;

_ если I = 0.

Определение 1. Систему ограничений (6) будем называть регулярной, если выполняются следующие условия:

k < n;

rank (A) = k;

dim(M) = n — k;

V v £ M : rank

Cxl)

(21) (22) (23)

min(k + l,n), (24)

где l — количество граничных гиперплоскостей, проходящих через точку v, A _v — матрица размера l times n , строками которой являются коэффициенты уравнений граничных гиперплоскостей, проходящих через точку \bfitv .

Условие (21) означает, что количество уравнений в системе ограничений должно быть меньше размерности пространства (в противном случае допустимый многогранник M вырождается в точку). Условие (22) говорит, что опорная матрица A должна иметь полный ранг, то есть среди ограничений не должно быть уравнений, задающих различные параллельные гиперплоскости. Условие (23) требует, чтобы допустимый многогранник M имел размерность, равную n - k . Это означает, что в системе ограничений не может быть неявных равенст в4 . Согласно условию (24) в системе ограничений не должно быть избыточных равенств, и при этом ранг матрицы коэффициентов неравенств, содержащих граничную точку, должен быть равным минимуму от числа неравенств и размерности пространства. Заметим, что для любой системы линейных ограничений, областью допустимых решений которой является ограниченное множество размерности больше 0, существует ее эквивалентное представление с регулярной системой ограничений в пространстве той же размерности (см. [11] , теорема 2.15).

Везде далее будем предполагать, что система ограничений (6) является регулярной. Это обеспечивает корректность всех последующих утверждений и алгоритмов. Следующее утверждение является теоретической основой для построения алгоритма VeSP.

Утверждение 1. Пусть выполняются условия (21) – (24) . Пусть через точку \bfitv in M проходит l граничных гиперплоскостей. Обозначим через I _v множество индексов этих граничных гиперплоскостей:

v £ П HI i . (25)

i \in I \bfitv

Положим

S \bfitv

( П Hi i]

\ ie l.    /

_\BbbR n _,

_

\cap S,

если I _v = 0 ;

если I _v = 0;

F = M П S _v .

Тогда множество F является гранью допустимого многогранника M и

dim(F) = n — min(k + l,n).

Доказательство. Сначала предположим, что l = 0, то есть через точку v не проходит ни одной граничной гиперплоскости. Следовательно, I _v = 0 . Тогда в силу (20) и (26) имеем

S _v = S.

С учетом (16) отсюда следует

M subseteq S \bfitv .

Принимая во внимание (27) , таким образом получаем

F = M.

Сам многогранник M является своей гранью [11] . Так как система ограничений (6) по предположению является регулярной, из (23) и (29) следует dim(F) = n — k. Таким образом, для l = 0 утверждение доказано.

Пусть теперь l >  0, то есть I _v = 0 . В силу (11) , (17) и (25) для любого i G I _v имеем

M С P i ;

M П H i = 0 .

Это — достаточные условия для того, чтобы множество F i = M П H i являлось гранью выпуклого многогранника M (см. [11] , определение 2.1). Пересечение граней многогранника M — снова грань многогранника M (см. [11] , утверждение 2.3). Поэтому множество

G = M П

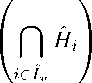
является гранью многогранника M . Покажем, что F = G . Сначала предположим, что I = 0 .

Тогда из (26) следует

S . = П Hi i .

i \in I \bfitv

С учетом (27) и (30) отсюда получаем

F = M П S _v = M П

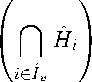
= M П S _v = G,

то есть F является гранью допустимого многогранника M. Пусть теперь I = 0 . Тогда с учетом (16) , (20) , (26) и (30) имеем

G = M П

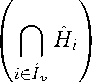
= M П

Hi   cap iel   /

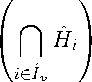
= M П

_

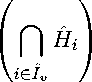
П S = M П S _v = F,

то есть и в этом случае F является гранью допустимого многогранника M . Вычислим размерность F для случая l >  0. Для этого заметим, что из (22) следует

_ dim(S) = n — k.

В силу (16) и (23) отсюда получаем, что подпространство S является аффинной оболочкой допустимого многогранника M :

_ aff(M) = S.

Из (20) и (26) следует

_

S subseteq S \bfitv .

Обозначим через Av матрицу размера l х n, содержащую коэффициенты граничных уравнений с индексами из Iv. Так как система ограничений (6) по предположению является регулярной, то в соответствии с определением 1 выполняется равенство rank

(IЛ)

= min(k + l,n).

Принимая во внимание (26), отсюда следует dim(S„) = n — min(k + l, n).

Учитывая, что аффинная оболочка подпространства есть само это подпространство, и принимая во внимание (27), (31), (32) и (33), имеем dim(F) = dim(aff(F)) = dim(aff(M) П Sv) = dim(S П Sv) = dim(S„) = n — min(k + l,n).

□

Утверждение доказано.

Определение 2. Собственной гранью точки \bfitv in M будем называть грань наименьшей размерности, содержащую точку \bfitv .

Утверждение 2. Точка \bfitv in M имеет только одну собственную грань.

Доказательство. Предположим, имеются две различные грани F ^\prime и F ^\prime\prime минимальной размерности, содержащие точку \bfitv . Поскольку пересечение граней допустимого многогранника M является гранью допустимого многогранника M , то F ^\prime cap F ^\prime\prime будет гранью допустимого многогранника M , имеющей размерность меньше минимальной, и содержащей точку \bfitv . Пришли к противоречию.

Обозначим через face(v) собственную грань точки г G M .

Утверждение 3. Пусть \bfitv \in M . Тогда собственная грань точки \bfitv может быть вычислена по формуле

face(v) =

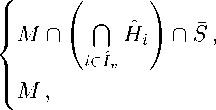
если I _v = 0 ;

если I _v = 0 ,

Л где I\bfitv — множество индексов всех граничных гиперплоскостей, содержащих точку \bfitv .

Доказательство. Положим

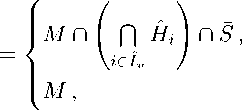
если I _v = 0;

если I _v = 0 ,

где I _v — множество индексов всех граничных гиперплоскостей, содержащих точку г. Множество F является гранью допустимого многогранника M в соответствии с утверждением 1. Грань F имеет минимальную размерность среди всех граней, содержащих точку \bfitv , так как она является подмножеством пересечения всех граничных гиперплоскостей, проходящих через \bfitv.

Следствие 1. Пусть \bfitv \in M. Тогда dim(face(v)) = n — min(k + l,n),                           (35)

где l — количество граничных гиперплоскостей, проходящих через точку \bfitv.

□

Доказательство. Следует непосредственно из утверждений 1 и 3.

Следствие 2. Пусть через точку \bfitv \in M проходят n - k или более граничных гиперплоскостей. Тогда dim(face(v)) = 0, то есть точка г является вершиной допустимого многогранника M .

Следствие 3. Пусть через точку г G M проходят n — к — 1 граничных гиперплоскостей. Тогда dim(face(v)) = 1, то есть грань face(v) является ребром допустимого многогранника M .

Следствие 4. Пусть через точку г G M проходит 0 граничных гиперплоскостей. Тогда dim(face(v)) = n — к и face(v) = M , то есть сам допустимый многогранник M является собственной гранью точки \bfitv.

Доказательство. Следует непосредственно из формул (23) , (35) и утверждения (2) .

2.    Формализованное описание алгоритма VeSP

Этот раздел посвящен формализованному описанию алгоритма VeSP, вычисляющего вершину допустимого многогранника. Алгоритм VeSP начинает свою работу в произвольной точке U q , принадлежащей некоторой грани F q допустимого многогранника M . Обозначим через I q размерность этой грани. Двигаясь по прямой в произвольном направлении по грани F q , алгоритм VeSP достигает ее границы в некоторой точке и. Эта точка будет 2025, т. 14, № 3 13

находиться на грани F 1 , размерность которой l 1 будет меньше l 0 . Продолжая движение по граням допустимого многогранника описанным образом, алгоритм VeSP за конечное число шагов придет к точке \bfitv k , лежащей на грани F k , имеющей размерность 0. Точка \bfitv k и будет искомой вершиной допустимого многогранника.

Основной функцией, используемой алгоритмом VeSP, является функция MoveAlongFace( - ), выполняющая прохождение грани допустимого многогранника. Эта функция, в свою очередь, использует следующие две функции: k j ( • ) — вычисление ортогональной проекции на подпространство и Jump( ^ ) — перемещение по направляющему вектору.

Рассмотрим сначала функцию вычисления ортогональной проекции k j (ж) точки ж на подпространство

S j = Q H i (J с I и i), (36) i \in J

При построении ортогональной проекции мы не различаем граничные и опорные гиперплоскости. Мы также предполагаем, что S j = 0 . Обозначим через A j матрицу коэффициентов уравнений с индексами из множества J , через \bfitb J — столбец правых частей этих уравнений. В случае, когда система уравнений A j ж = b j является совместной, и матрица A j A T является невырожденной, ортогональная проекция точки \bfitx на подпространство S J может быть вычислена по следующей формуле [12] :

k j (ж) = ж - A T ( Aj A T ) 1 ( A j ж - b j ) . (37)

Для того, чтобы гарантировать невырожденность матрицы A J A _J ^T в общем случае, необходимо из множества J удалить индексы всех избыточных уравнени й5 . Получившееся множество J ^\prime будет обладать следующими свойствами:

S j = S j ' ;

rank(A j ) = rank(A j / ); det (A j ' A T ) = 0.

Если, тем не менее, не удается построить обратную матрицу к матрице A J \prime A _J ^T \prime , например, в следствии потери точности, то в этом случае можно приближенно вычислить ортогональную проекцию точки на подпространство, используя алгоритм Качмажа [13, 14] .

Далее рассмотрим функцию Jump(ж, d ), осуществляющую перемещение по направляющему вектору \bfitd от допустимой точки \bfitx к допустимой точке, максимально удаленной от \bfitx. Основной элементарной операцией, используемой для перемещения, является d-проекция 7 ^ (ж) точки ж на граничную гиперплоскость H i по направлению вектора d, вычисляемая по формуле

7 ? (ж) =

\langle \bfita i , \bfitx \rangle- b i \langle \bfita i , \bfitd \rangle

\bfitd ,

если если

(a,, d) = 0;

( a , , d = 0

(см. определение 1 и утверждение 2 в [15] ). Реализация функции Jump(ж, d) представлена в виде алгоритма 1.

Алгоритм 1 Реализация функции Jump(x, d)

Require: х G M ; V i G I : x + d G Й i

• 1:    function Jump(x, d)

• 2:     ^x min ^{: = x}

• 3:     for i G I do

• 4:          if (a i , d) > 0 then

• 5:              ^x 7 ^:= 4i^{( x )}

• 6:             if ||x₇ - x | <  ^x min - x | then

• 7:                x min := x₇

• 8:             end if

• 9:         end if

• 10:     end for

• 11:       return \bfitx_m i _n

• 12:    end function

Для работы алгоритма необходимо, чтобы точка х принадлежала допустимому многограннику М, и выполнялось условие

^^н                                    __

ViGl:x + dG Н{, которое означает, что точка, получающаяся путем прибавления вектора d к точке ж, должна принадлежать всем опорным гиперплоскостям (13). Другими словами, точка {x+d) обязана удовлетворять всем уравнениям из системы ограничений (6). Схема работы алгоритма 1 проиллюстрирована на рис. 1.

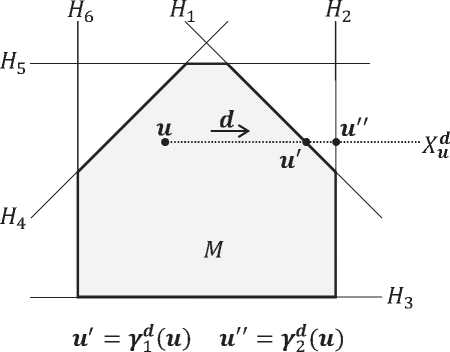
Рис. 1. Действие функции Jump: Jump(u, d) = и'.

В приведенном примере изображен многогранник M , образованный пересечением шести полупространств

P 1 = { ж G R n |( a 1 , ж ) <  Ь 1 } ;

Р б = { ж G R n |( a 6 , ж ) ^ Ь б } .

Эти полупространства ограниченны гиперплоскостями

H i = { ж G R n |( a i , ж ) = b i } ; ...........................

Н б = { ж G K n |( a ₆ , ж ) = Ь б } .

Заданы точка \bfitu \in M и направляющий вектор \bfitd. Необходимо перенести точку \bfitu по направлению вектора \bfitd в максимально удаленную точку \bfitu ^\prime \in M. Известно [16] , что луч

Xu = { ж G Rn| ж = и + Xd, A ^ 0} пересечет гиперплоскость Hi (i = 1,..., 6) только в том случае, когда

( a i , d) >  0.                                               (40)

Проверка условия (40) на шаге 4 алгоритма 1 в этом случае покажет, что луч X _\bfitu ^\bfitd пересечет только гиперплоскости H i и Н 2 . Шаги 5-8 алгоритма 1 вычислят d-проекции 7 ^ (и) и 7 2 (и) на гиперплоскости H , H 2 и выберут ту из них, которая находится ближе всего к точке \bfitu. Это будет U = 7 ^ (и).

Реализация функции MoveAlongFace(v), осуществляющей прохождение грани допустимого многогранника, представлена в виде алгоритма 2. Прокомментируем этот алгоритм. Начальная точка \bfitv должна принадлежать допустимому многограннику M и не являться его вершиной. На шагах 2–7 строится множество I _\bfitv , включающее в себя индексы всех опорных гиперплоскостей и индексы граничных гиперплоскостей, проходящих через точку \bfitv . На шагах 8–13 из множества I \bfitv удаляются индексы избыточных уравнений в случае, когда они там присутствуют. Если I _v = 0 , то далее выполняются шаги 15—19, в результате чего вычисляется точка w G aff(face(v)) такая, что w = v. Для этого на шаге 16 генерируется случайный вектор \bfitc \in \BbbR ⁿ . Используя этот вектор, шаг 17 вычисляет точку \bfitu, удаленную от \bfitv на расстояние \delta. Здесь \delta — «большой» положительный параметр: чем больше \delta, тем точнее будет вычислен направляющий вектор d, используемый функцией Jump( - ). Шаг 18 вычисляет точку \bfitw , являющуюся ортогональной проекцией точки \bfitu на подпространство aff(face(v)) с помощью формулы (37) . Если сгенерированный вектор с случайно оказался перпендикулярным к подпространству aff(face(v)), то есть

Vi G Iv : (ai, с) = 0, то мы получим v = w. В этом случае на шаге 16 генерируется новый случайный вектор с и повторно вычисляются точки и и w (шаги 17, 18). Если на шаге 19 v = w, то происходит выход из цикла repeat/until. При Iv = 0 вместо шагов 15—19 выполняется шаг 22, который 16 Вестник ЮУрГУ. Серия «Вычислительная математика и информатика»

Алгоритм 2 Прохождение грани

Require: \bfitv \in M; \mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitv)) > 0

1: function \mathrm{M}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{A}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{F}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitv)

2:

3:

4:

6:

7:

8:

9:

10:

11:

12:

13:

14:

16:

17:

18:

19:

20:

21:

22:

23:

24:

25:

26:

27:

28:

29:

30:

_

I\bfitv :=I for i = 1, . . . , m do if \bfitv \in H\^ i then

I\bfitv := I\bfitv \cup \{i\} end if end for

\bfitv:= \bfitv for i G I!„ do if rank(AI _^) = rank(AI ) then

I\bfitv := I\bfitv - \{i\} end if end for if I\bfitv \not= \emptyset then repeat

\bfitc := \mathrm{R}\mathrm{a}\mathrm{n}\mathrm{d}\mathrm{o}\mathrm{m}\mathrm{N}\mathrm{o}\mathrm{n}\mathrm{Z}\mathrm{e}\mathrm{r}\mathrm{o}\mathrm{V}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}()

\bfitu :=\bfitv + \delta \bfitc / \| \bfitc \|

\bfitw := \bfitpi I _\bfitv (\bfitu)

until \bfitv \not= \bfitw end if if I\bfitv = \emptyset then

\bfitw := \bfitpi 1 (\bfitv)

end if if \langle\bfitc, \bfitw\rangle > \langle\bfitc, \bfitv\rangle then

\bfitd:=\bfitw-\bfitv else

\bfitd:=\bfitv-\bfitw end if

\bfitv next :=\mathrm{J}\mathrm{u}\mathrm{m}\mathrm{p}(\bfitv , \bfitd)

return \bfitv next

31: end function

в качестве \bfitw выбирает ортогональную проекцию точки \bfitv на граничную гиперплоскость с индексом 1 по следующей формуле [12] :

\langle \bfita 1 , \bfitv \rangle - b 1

\bfitpi 1 (\bfitv) = \bfitv -                                    \bfita 1 .

\| \bfita 1 \| ²

Из I _\bfitv = \emptyset следует, что точка \bfitv является внутренней точкой допустимого многогранника M . Поэтому \bfitv \not = \bfitw. Шаги 24–28 вычисляют направляющий вектор \bfitd \not = \bfzero , ведущий к увеличению значения целевой функции. В завершение на шаге 29 с помощью вызова функции \mathrm{J}\mathrm{u}\mathrm{m}\mathrm{p}(\bfitv , \bfitd) осуществляется переход по этому направлению к новой граничной точке \bfitv _next , которая возвращается в качестве результата на шаге 30.

Функция MoveAlongFace( - ) в качестве аргумента требует точку V , принадлежащую допустимому многограннику M . Такую точку можно получить с помощью метода релаксации Агмона—Моцкина—Шёнберга [17, 18] . При этом систему общего вида (6) необходимо будет привести к стандартному виду (1) .

Реализация алгоритма VeSP, выполняющего поиск вершины допустимого многогранника M, определяемого системой ограничений (6) , представлена в виде алгоритма 3.

Алгоритм 3 VeSP (Vertex Seeking by Pro jecting)

Require: \bfitv 0 \in M

• 1:    t :=0

• 2:    while dim(face(v t )) > 0 do

• 3:     v t+1 := MoveAlongFace(v t )

• 4:      t := t + 1

• 5:    end while

• 6:    output V _t

• 7:    stop

Прокомментируем шаги этого алгоритма. Шаг 1 устанавливает счетчик итераций t в значение 0. Шаг 2 открывает цикл while вычисления вершины многогранника. Если размерность грани, на которой лежит точка \bfitv t , больше нуля, выполняется шаг 3, который с помощью функции MoveAlongFace( - ) (см. алгоритм 2) осуществляет переход к точке v t+i , лежащей на грани меньшей размерности. После этого выполняется шаг 4, увеличивающий счетчик итераций t на единицу, и выполняется переход на начало цикла while . Если условие цикла while на шаге 2 не выполняется, то точка \bfitv _t является вершиной допустимого многогранника M . В этом случае выполняется переход на шаг 6, который выводит точку \bfitv _t в качестве результата. Шаг 7 завершает работу алгоритма.

Сходимость алгоритма 3 к вершине допустимого многогранника за конечное число итераций гарантируется следующей теоремой.

Теорема 1. (Сходимость алгоритма VeSP) Пусть система ограничений (6) является регулярной, то есть выполняются условия определения 1. Обозначим через

\bfitv 0 , \bfitv 1 , . . . , \bfitv t , . . .                                                                                                     (41)

последовательность точек, генерируемых алгоритмом 3. Тогда эта последовательность сходится к точке, являющейся вершиной допустимого многогранника M , не более, чем за n итераций, где n — размерность пространства:

3t' <  n : dim(face(v _t )) = 0.

Доказательство. Если dim(face(v o )) =0 то точка V o является вершиной допустимого многогранника M . В этом случае алгоритм 3 выводит \bfitv 0 в качестве результата и на этом заканчивает свою работу.

Пусть начальная точка \bfitv 0 вершиной не является. В этом случае последовательность (41) содержит более одного элемента. Пусть \bfitv t — произвольный не конечный элемент последо-

А.Э. Жулев, Л.Б. Соколинский, И.М. Соколинская вательности (41) , то есть \bfitv _t не является вершиной:

\mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitv t )) > 0.                                                                                                                                                                            (42)

В соответствии с (35) имеем

\mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitvt)) = n - \mathrm{m}\mathrm{i}\mathrm{n}(k + l, n), где l — количество граничных гиперплоскостей, проходящих через точку \bfitvt . В силу (42) отсюда получаем k+l

и

\mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitvt)) = n - k - l.(44)

Шаг 3 алгоритма 3 с помощью вызова функции \mathrm{M}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{A}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{F}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitv_t), реализуемой алгоритмом 2, генерирует следующий элемент ^₊1. Проанализируем работу алгоритма 2. Точке \bfitv_tв этом алгоритме соответствует точка \bfitv :

\bfitv \equiv \bfitvt.(45)

Из (44) и (45) следует

\mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitv)) = n - k - l.(46)

На шагах 2–7 алгоритма 2 формируется множество I_\bfitv, включающее в себя индексы всех опорных и граничных гиперплоскостей, проходящих через точку \bfitv . Так как по условию теоремы система ограничений является регулярной, то из (43) и (24) следует, что множество I_\bfitv не содержит индексов избыточных уравнений.

Предположим сначала, что I_\bfitv\not= \emptyset. В этом случае выполняются шаги 15–19. Обозначим через S_\bfitvподпространство, являющееся аффинной оболочкой грани \mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitv):

S\bfitv = ^\bigcapHi .

i\inI\bfitv

На шагах 15–19 вычисляется точка \bfitw \in S_\bfitv, отличная от точки \bfitv. С использованием этих точек шаги 24–28 формируют ненулевой направляющий вектор \bfitd = \bfitw - \bfitv , задающий луч

\mathrm{r}\mathrm{a}\mathrm{y}(\bfitv, \bfitd) = \{ \bfitx \in \BbbRⁿ| \bfitx = \bfitv + \lambda\bfitd, \lambda \geqslant 0\} .

По построению этот луч принадлежит подпространству S_\bfitv:

\mathrm{r}\mathrm{a}\mathrm{y}(\bfitv, \bfitd) \subseteq S\bfitv.                                                                                                                                                                                    (47)

На шаге 29 с помощью вызова функции \mathrm{J}\mathrm{u}\mathrm{m}\mathrm{p}(\bfitv, \bfitd) (см. алгоритм 1) вычисляется точка \bfitvnext \in M , являющаяся пересечением луча \mathrm{r}\mathrm{a}\mathrm{y}(\bfitv, \bfitd) с ближайшей граничной гиперплоскостью H^{\^}i\prime такой, что i^\prime\in/ I_\bfitv. Такая гиперплоскость существует в силу ограниченности допустимого многогранника M. Из (47) следует, что через точку \bfitv_next проходит не менее l^\prime= l + 1 граничных гиперплоскостей. С учетом (35) и (43) отсюда получаем

\mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitvnext)) \leqslant n - k - l - 1.                                                                                                             (48)

Сопоставляя (46) и (48), имеем

\mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitv)) > \mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitvnext)).

Теперь предположим, что I_\bfitv= \emptyset, то есть k = 0 и l = 0. В соответствии со следствием 4 отсюда следует

\mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitv)) = n.                                                                                                                                                                             (49)

В этом случае выполняется шаг 22, в результате которого мы получаем точку \bfitw на граничной гиперплоскости HI 1. Так как через v не проходит ни одной граничной гиперплоскости, то \bfitv \not= \bfitw . Шаги 24–28 формируется ненулевой направляющий вектор \bfitd = \bfitw - \bfitv, задающий луч \mathrm{r}\mathrm{a}\mathrm{y}(\bfitv, \bfitd). На шаге 29 с помощью вызова функции \mathrm{J}\mathrm{u}\mathrm{m}\mathrm{p}(\bfitv, \bfitd) (см. алгоритм 1) вычисляется точка \bfitv_next\in M , являющаяся пересечением луча \mathrm{r}\mathrm{a}\mathrm{y}(\bfitv, \bfitd) с ближайшей граничной гиперплоскостью. Таким образом, через точку \bfitv_nextпроходит не менее одной граничной гиперплоскости. В соответствии с (35) отсюда следует

\mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitvnext)) \leqslant n - 1.(50)

Сопоставляя (49) и (50), и в этом случае имеем

\mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitv)) > \mathrm{d}\mathrm{i}\mathrm{m}(\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitvnext)).(51)

Точка \bfitvnext на шаге 30 возвращается как результат вызова функции \mathrm{M}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{A}\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{F}\mathrm{a}\mathrm{c}\mathrm{e}(\bfitvt) в алгоритме 3 на шаге 3. Поэтому vnext = vt+1-

Из 45, 51 и 52 следует dim(face(vt)) > dim(face(vt+i)).(53)

Таким образом, последовательности (41) соответствует убывающая последовательность неотрицательных целых чисел dim(face(vg)) > dim(face(vi)) > • • • > dim(face(vt)) > ..., ограниченная сверху числом, равным размерности пространства n. Следовательно, последовательность (41) имеет длину не более n + 1. Осталось заметить, что в соответствии с условием выхода из цикла while (шаг 2), последним элементом последовательности (41) будет некоторая вершина допустимого многогранника M . Теорема доказана.

3. Реализация и вычислительные эксперименты

Нами была выполнена реализация алгоритма VeSP на языке C++, исходные коды которой свободно доступны на Мы протестировали алгоритм VeSP на эталонных задачах из репозитория Netlib-LP [19, 20], доступного по адресу Тестирование выполнялось на персональном компьютере с процессором Intel Core i7-13620H 2.40 GHz, DDR5 32 ГБ. Результаты тестирования представлены в табл. 1.

В заголовке таблицы использованы следующие обозначения: в колонке «Задача» указано имя задачи ЛП из репозитория Netlib-LP; m — количество ограничений; n — количество переменных (размерность пространства решений); \mathrm{d}\mathrm{i}\mathrm{m}(M) — размерность многогранника

Таблица 1. Результаты тестирования алгоритма VeSP на задачах Netlib-LP

Задача	m	n	\mathrm{d}\mathrm{i}\mathrm{m}(M)	\langle\bfitc, \bfitu0\rangle	Итер.	\langle\bfitc, \bfitv\rangle	Время	\mathrm{d}\mathrm{i}\mathrm{s}\mathrm{t}(\bfitv, M)
adlittle	56	97	82	0.106230 \times 108	44	0.716431 \times 106	0	2.3 х 10-7
afiro	27	32	24	0.532704 \times 102	6	-0.309501 \times 102	0	9.9 х 10-11
beaconfd	173	262	122	0.338431 \times 105	35	0.337284 \times 105	2	1.5 х 10-11
blend*	74	83	40	-0.508862 \times 101	18	-0.158981 \times 102	775	1.1 х 10-12
fit1d	24	1026	1025	-0.483981 \times 104	530	-0.899543 \times 104	614	4.0 х 10-7
grow7	140	301	161	-0.207633 \times 108	119	-0.439694 \times 108	2	9.7 х 10-6
israel	174	142	142	0.307907 \times 107	45	-0.102957 \times 106	0	5.9 х 10-7
kb2	43	41	25	-0.560444	2	-0.174527 \times 103	0	2.2 х 10-10
recipe	91	180	92	-0.230604 \times 103	9	-0.262820 \times 103	0	1.5 х 10-12
sc105	104	103	58	-0.537203 х 10-2	7	-0.981874 \times 101	0	3.6 х 10-11
sc50a	49	48	28	-0.710608 х 10-1	7	-0.414361 \times 102	0	9.0 х 10-12
sc50b	48	48	28	-0.107994	13	-0.478109 \times 102	0	4.9 х 10-12
scagr7	129	140	56	-0.174392 \times 107	22	-0.202156 \times 107	0	3.9 х 10-8
share2b	96	79	66	-0.368733 \times 103	10	-0.389506 \times 103	0	1.3 х 10-7
stocfor1	117	111	48	-0.254283 \times 105	8	-0.254636 \times 105	0	1.1 х 10-12

’Применен итерационный алгоритм Качмажа.

допустимых решений, вычисляемая по формуле dim(M) = n — rank(A), где A — матрица коэффициентов уравнений, входящих в систему ограничений; (с, uq) — значение целевой функции в начальной точке ио g M; в колонке «Итер.» указано количество итераций, выполненных алгоритмом 3 при поиске вершины многогранника M; (с, и) — значение целевой функции в найденной вершине и; «Время» — затраченное время в секундах; dist(v, M) — точность решения, вычисляемая как евклидово расстояние от точки и до многогранника M.

Начальная точка ио g M вычислялась с помощью написанных нами программ FIP и Quest. Программа FIP (Feasible point Iterative Projection) стартует из точки Жо = 0 и находит точку Zq, принадлежащую допустимому многограннику M. В основе программы FIP лежит метод релаксаций Агмона—Моцкина—Шёнберга [17, 18]. Исходные коды этой программы доступны на Полученная точка Zq g M использовалась программой Quest для нахождения так называемой точки апекса \bfitu0, которая представляла собой «грубое» приближение к решению задачи ЛП [21]. Эта точка использовалась алгоритмом VeSP в качестве начального приближения. Исходные коды программы Quest доступны на

Проведенные эксперименты показали, что алгоритм VeSP успешно нашел вершину допустимого многогранника для всех 15 задач, выбранных из репозитория Netlib-LP. Время вычислений для задач с числом переменных n< 200, за исключением задачи «blend», составило менее половины секунды. Задачи «beaconfd» и «grow7» с количеством переменных 262 и 301 соответственно потребовали 2 секунды процессорного времени. При решении задачи «fit1d», содержащей 1026 переменных, алгоритм VeSP в процессе поиска вершины выполнил 513 итераций, что потребовало более 10 минут. Таким образом, можно сделать вывод, что время работы алгоритма VeSP существенно зависит от размерности задачи. Что касается задачи «blend» с числом переменных 83, для нее не удалось вычислить обратную матрицу в формуле (37) по причине потери точности при использовании 64-разрядной вещественной арифметики. Поэтому для приближенного вычисления ортогональных проекций (шаги 18, 22 алгоритма 2) пришлось использовать итерационный алгоритм Качмажа. По этой причине 18 итераций, выполненных алгоритмом VeSP для этой задачи, заняли 13 минут.

При этом более 99% процессорного времени было затрачено на вычисление ортогональных проекций. Это объясняется тем, что итерационный алгоритм Качмажа имеет линейную скорость сходимости [22]:

||Xk - KJ(xo)| < 0\\Xk-1 - KJ(xo)| с вещественной константой 0 < в < 1. Здесь {xi,..., Xk-i, Xk,... } — последовательные приближения к ортогональной проекции kj (xo) точки Xo на подпространство Sj , вычисляемые алгоритмом Качмажа. Константа \theta зависит только от углов между гиперплоскостями Hi (i G J). При малых углах значение в приближается к единице, и скорость сходимости стремится к нулю. Проведенные эксперименты также показали, что точность вычисления координат вершины допустимого многогранника находится в обратной пропорции относительно количества выполненных итераций.

Заключение

В статье предложен новый проекционный алгоритм VeSP для нахождения вершины многогранника допустимых решений системы линейных ограничений. Под системой линейных ограничений понимается система общего вида, включающая в себя как линейные неравенства, так и линейные уравнения. Подобные системы ограничений характерны для задач линейного программирования. В качестве стартовой точки алгоритм VeSP использует произвольную точку многогранника допустимых решений. Алгоритм VeSP применим к любым системам линейных ограничений, имеющим непустую ограниченную область допустимых решений. Доказано утверждение, позволяющее для заданной допустимой точки вычислить ее собственную грань (грань наименьшей размерности, содержащую эту точку). В качестве следствий получены достаточные условия для того, чтобы собственная грань допустимой точки была вершиной, ребром или многогранником допустимых решений. Представлено формализованное описание алгоритма VeSP на псевдокоде. Также представлены формализованные описания двух подпрограмм-функций, используемых алгоритмом VeSP: подпрограмма-функция, осуществляющая перемещение по направляющему вектору от заданной допустимой точки к максимально удаленной допустимой точке, и подпрограмма-функция прохождения грани многогранника. Доказана теорема сходимости алгоритма VeSP к вершине многогранника допустимых решений за количество итераций, не превышающих размерность пространства. Выполнена реализация алгоритма VeSP на языке программирования C++. Указанная реализация была протестирована на эталонных задачах из репозитория Netlib-LP. Эксперименты показали, что алгоритм VeSP способен эффективно находить базисное решение для реальных задач ЛП. Основным преимуществом алгоритма VeSP является то, что он гарантированно находит вершину многогранника допустимых решений не более, чем за n итераций. Алгоритмам, основанным на симплекс-методе и методе исключения переменных Фурье—Моцкина, для этого может понадобиться 2n и 2n/2 итераций соответственно.

Обозначения n       число переменных в системе ограничений (размерность пространства)

m       количество неравенств в системе ограничений k        количество уравнений в системе ограничений

\BbbRd       вещественное евклидово пространство размерности d langlecdot, cdotrangle

^

A

_

A

^

\bfitb

_

\bfitb

\bfitai

Z4 I

I

Pi

Hi Hi

M

S

M aff(X) dim(X) face(v) rank( A) |cdot|

скалярное произведение двух векторов матрица коэффициентов неравенств: A G Kmxn матрица коэффициентов уравнений: A in \BbbRk\timesn столбец правых частей неравенств: b G Rm столбец правых частей уравнений: \bfitb in \BbbRk a"I i-тая строка матрицы A (i = 1,..., m + k)

A      A

л

л

индексы (номера) строк матрицы A: I = {1,..., т}

индексы (номера) строк матрицы A: I = {m + 1,..., m + k} полупространство, определяемое формулой [ai, ж) ^ bi при i G I граничная гиперплоскость полупространства Pi опорная гиперплоскость, определяемая уравнением [ai, ж) = bi граничный многогранник (пересечение всех полупространств Pi) опорное подпространство (пересечение всех опорных гиперплоскостей Hi) допустимый многогранник (область допустимых решений): M = M П S аффинная оболочка множества X размерность множества X: dim(X) = dim(aff(X))

собственная грань точки \bfitv in M ранг матрицы A евклидова норма