О выделении разрывов в расчетах динамики несжимаемой упругой среды

Основная трудность в численных расчетах существенно нестационарных задач механики сплошных сред связана с возникновением и последующим распространением в среде поверхностей разрывов. Закономерности движения этих поверхностей определяются только из решения соответствующей краевой задачи, и потому положение таких поверхностей, а также величины разрывов обязательно должны отслеживаться на каждом временном шаге алгоритма. В газовой динамике подобные алгоритмы — их называют алгоритмами выделения разрывов — давно и хорошо известны [1–7]. Однако большинство из них в динамике деформирования применить непосредственно невозможно. Связано это главным образом с тем, что в деформируемой в условиях динамического нагружения среде одновременно присутствуют два процесса: распространение объемных деформаций (как и в газовой динамике) и

распространение деформаций изменения формы. Процессы взаимосвязаны и взаимозависимы, поэтому разрывы оказываются комбинированными. Из-за этого, например, затруднительно рассчитать распад разрыва, и потому непосредственное приложение метода выделения разрыва С.К. Годунова становится невозможным. Выход из такого положения находят в использовании схем сквозного счета [8–13] и их многочисленных модификаций. Но такой подход не является универсальным, тем более что немонотонность схем в этом случае заставляет прибегать к специальным приемам, в частности к введению искусственной вязкости, что вызывает неоправданное сглаживание разрывов. Как пример монотонной схемы отметим построенную в [10] схему второго порядка точности, свободную от указанного недостатка.

При необходимости непосредственного выделения разрывов, например, при взаимодействии волн между собой и с преградами, построение численных алгоритмов испытанными методами газовой динамики, как уже отмечалось, встречает большие трудности. В работе [14], по-видимому, впервые предложено для целей алгоритмического выделения разрывов в численных расчетах встраивать в численную разностную схему прифронтовые лучевые разложения решения. Таким способом рассчитывался процесс распространения плоских ударных волн в одномерном случае. В работе [15] этот же алгоритмический прием применен к одномерной задаче с осевой симметрией.

Здесь так же, как и в [15], рассмотрим осесимметричную задачу, но отличную в том, что принимается условие присутствия деформаций, предваряющих поверхности разрывов. Это обстоятельство приводит к тому, что передний фронт распространяющихся вглубь несжимаемой среды деформаций изменения формы разделяется на две поверхности разрывов. Особенности построения лучевых разложений при этом и способы их встраивания в разностную схему, записанную вне прифронтовой области, являются предметом настоящей публикации. Заметим, что в работе [16] построено приближенное решение задачи в аналогичной постановке, но в качестве прифронтовых разложений используются решения эволюционных уравнений, которые также можно было бы употребить для целей выделения разрывов, но только при малой интенсивности ударных волн.

Приближенный метод решения задачи динамического деформирования в форме степенного ряда по лучевой координате [8] или по времени [17], когда коэффициенты ряда находятся путем решения задачи для вытекающего из уравнений модели обыкновенного дифференциального уравнения (уравнения затухания), известен давно. Наличие достаточно полного и квалифицированного обзора [18] избавляет от необходимости вникать в историю развития этого метода. Отметим только принципиальную особенность в приложении метода тогда, когда лучевое разложение строится за поверхностью сильных разрывов (за ударной волной). При этом из-за несовпадений скоростей распространения по среде возмущений и ударных волн обыкновенные дифференциальные уравнения для коэффициентов лучевых рядов не вытекают из уравнений модели, и требуются иные подходы [19, 20]. Нужно отметить еще публикацию [21], где лучевая асимптотика использовалась для выделения разрывов в случае криволинейных и расходящихся лучей, но при распространении одной ударной волны.

• 2.    Исходные модельные зависимости

Движение изотропной несжимаемой упругой среды в ее адиабатическом приближении свяжем первоначально с прямоугольной системой пространственных координат x ₁, x ₂, x ₃ , . Тогда в переменных Эйлера имеем систему уравнений

С у,j = Р a i ,

д V,          д v а = v+vv.. V. = — v =— 1       1 j 1 , j ,          1      д t ’         1, j     д x j ди,           д u v,. = и, + vu ,, Ui = —i- , и i= —-,                                (1) 1      1      11 , 1 ,         1       д t            1 , 1      д x j c ij = - P ^ У + до” (^ kj — 2 a kj ) , 2 a 1j = Ui,j + uj ,1- u k,1 u k,j-

Здесь: u i , v,, a i — компоненты векторов перемещений, скоростей и ускорений; a j , c j — компоненты тензоров деформаций Альманси и напряжений Коши–Эйлера; P — добавочное всестороннее давление; р = const — плотность среды.

Система уравнений (1) окажется замкнутой, если задать упругий потенциал (плотность распределения внутренней энергии) W = W(11,12) в форме разложения в ряд Тейлора в окрестности свободного состояния среды:

W — W ( 1 1 , 1 2 ) — — 2 ц 1 1 + bl 12 — ц 1 2 — aI ^ — ( ц — b ) 1 1 1 2 + ...,

1 1 ^{— a} kk ,      ¹ 2 ^{— a} ik ^a ki .

Постоянную ц соотносят обычно с модулем сдвига, тогда а и b — модули упругости третьего порядка. Сокращение числа упругих постоянных в (2) связано с характером изучаемого далее винтового движения среды [22]. Для компонент вектора перемещений в таком частном случае движения среды в цилиндрической системе координат r, ф, z принимаем распределения ur — r (1 — cos V( r, t)),     u ф — r sin V( r, t),     uz — u (r, t).

Таким образом, искомыми зависимыми переменными задачи являются осевое перемещение u ( r , t ) и крутка v ( r , t ). Для компонент тензора напряжений, следуя (1), получим зависимости:

ст„ — -P — 61 m - 62m2 +...,    ст — ст:: + цr2v2 — 63mu2, ii                                                                                                     'ф'ф              **                           , •                           , i ст zz — ст rr + ц u 2—03 mr 2у2.,    ст r ф — цг v, r (1+ Х1 m2 +...) —Р hr V, r, стrz — цu,r (1 + X1 m2 +...) —phu,r,     стфz — rv,ru,r (ц + 63m +...),                          (3)

m — ( r V , _r ) 2 + ( u , _r ) 2 , h — c ² ( 1 + X i m 2 + ... ) , c 2 — ц/p ,

6 1 — ( ц + b )/2,     6 2 — 3( ц + a — b )/4,     6 3 — ( b "P )/2, X 1 —6 2/ц .

В (3) и далее индексами после запятой обозначены частные производные функции по соответствующим переменным.

Подстановка (3) в уравнения движения приводит к системе трех дифференциальных уравнений относительно независимых переменных P(r, t), v(r, t) и u (r, t)

Pr + r ( цr v r + 63u r) + ®( 61 + 262m ) +... — rv t,

(1+ X1 m2 )(v,rr + 3r—1V,r) + 2X1®mV,r +... — c—2V,tt ,

(1+ X1 m2)(u,rr + r—1 u,r) + 2x1®mu,r +... — c—2u,tt,

®— 2 ( u,rru,r + r 2V,rr V,r + rV2r ) .

Первое из уравнений (4) служит для вычисления добавочного давления P ( r , t ) по найденным из двух других уравнений функциям v ( r , t ) и u ( r , t ). Многоточием в (4), как в (2) и (3), обозначены слагаемые с функциями v ( r , t ) и u ( r , t ) и их производными более высокого порядка, которые здесь опущены.

Передними фронтами распространяющихся по среде граничных ударных возмущений являются, как правило, ударные волны, то есть поверхности разрывов скоростей, деформаций и напряжений. Какие же поверхности разрывов при этом возникают?

Из закона сохранения импульса вытекает динамическое условие совместности разрывов:

[^ст -7 ] n j ^— Р ( v k n k ^— G ) [ v i ] .                                                 ⁽⁵⁾

Здесь: квадратные скобки обозначают разрыв функции на ударной волне, так что [ f ] — f ^{+ —} f ^— , где f ^{+ —} значение функции непосредственно перед поверхностью разрывов, а f ^— — сразу за такой поверхностью; n _j — компоненты единичной нормали в данной точке поверхности разрывов; G — скорость движения ударной волны в направлении ее нормали. В рассматриваемом случае из (5) следует

[ст rr ]— 0

[ст r ф]——Р G [ v ф],                                           2

[ст rz ]——Р G [ vz ].

Если в (6) подставить зависимости для напряжений из (3) и воспользоваться кинематическими условиями совместности разрывов Адамара [ ut ] —— G [ ur ], [vt ] —— G [vr ], то получим три уравнения, связывающих разрывы [ur. ], ^^r. ] и [P] при неизвестной скорости G . Соотношение (6)1 служит для вычисления [P] на поверхности разрывов, так же, как и (4)1 — для вычисления P(r,t), а (6)2 и (6)3 приводят к системе уравнений h [ r V, r ] + ( r V, r -[ r V, r ])[ h ] = G 2 [ r V, r ] , h [ u, r ] + (u, r-[ u, r ])[ h ] = G2 [ u, r ], [ h ] = G2 [ m ](x1 (m - 2[ m ]) +...).

2       (7)

Знаки « + » у параметров, вычисляющихся перед поверхностью разрывов, опущены, так как в (7) и далее встречаются только такие значения функций и величины разрывов. Умножим соотношение (7) 1 на [ u _r ] , (7)2 — на [ r v _r ] и вычтем второе произведение из первого. Таким способом найдем конечное выражение связи между [ u , _r ] и [ v , _r ] , которое следует назвать условием существования ударных волн:

[ h ] ( ^r v , r [ u , r ]^{- u} , r [ ^r V , r ] ) = 0.

В несжимаемой упругой среде одномерные цилиндрические ударные волны могут распространяться только в условиях (8), согласно которым возможно существование волн двух типов.

Тип 1. Пусть выполнение (8) обеспечивается равенством нулю выражения, стоящего в круглых скобках. Тогда r V, r       u, r

[ ^{r V} , r ] [ u , r ] .

Согласно (9) разрывы пропорциональны предварительным деформациям, и, значит, данная волна является плоскополяризованной. На такой поверхности разрывов меняется скачкообразно только интенсивность разрыва без изменения направления предварительных деформаций. Когда, например, u , _r = 0 , то на ударной волне [ u _r ] = 0, и u _r остается равной нулю и за этой поверхностью разрывов. Аналогично при v _r = 0 равен нулю разрыв [ r v _r ] , и после прохождения плоскополяризованной ударной волны v _r = 0. Одномерные плоские волны (ранее отмечались в [21,23,24]) назывались волной нагрузки. Термодинамические ограничения (аналог теоремы Цемплена для совершенного газа) в абсолютном большинстве случаев приводят к существованию только ударных волн [23], увеличивающих предварительный сдвиг, запрещая разгружающие плоскополяризованные разрывы. Для скорости распространения данной ударной волны G 1 , согласно (7), можно найти

G =

/                   X12

u h-[ h]+—[ h]

I           [ u , r ] J

Согласно (10) скорость распространения плоскополяризованной волны нагрузки зависит от предварительных деформаций в среде и интенсивности разрывов [ m ] и [ u , _r ] .

Тип 2. Существование второй ударной волны связано с выполнением (8) при условии [ h ] = [ m ] = 0 . На такой поверхности разрывов интенсивность предварительного сдвига остается неизменной ([ m ] = 0), и может скачкообразно поменяться только его направление. Эта поверхность разрывов названа в [21] ударной волной круговой поляризации, а в [23] — нейтральной ударной волной, являющейся изоэнтропической [23], и скорость ее G ₂ полностью определяется величиной предварительных деформаций

G ₂ = h ^1/2 .

Можно показать [23], что в упругой несжимаемой среде всегда справедливо неравенство: G 1 >  G ₂.

• 3.    Постановка задачи

Пусть несжимаемая упругая среда заполняет часть пространства, расположенную между жесткими цилиндрическими поверхностями r = r ₀ и r = R ( R >  r₀ ). Считаем, что на ограничивающих поверхностях выполняются условия жесткой спайки, при этом на поверхности r = R до начального момента времени t = 0 перемещения отсутствуют ( u ( R ,0) = 0), а поверхностью r = r ₀ несжимаемой среде сообщено поле деформаций, связанное с краевым условием u ( r ₀,0) = u ₀ = const .Итак, материал упругого слоя находится к моменту времени t = 0 в условиях антиплоского сдвига. Из решения уравнения равновесия с учетом зависимостей (3) легко вычисляется напряженно-деформированное состояние в слое. Далее полагаем его известным.

Считаем, что, начиная с момента времени t = 0, жесткий вал ( r <  r ₀) поворачивается по закону

у ( r ₀, t ) = у ₁ 1 + У 2 1 2 + ...,         u ( r ₀, t ) = u ₀.

Такое воздействие на материал слоя приведет к распространению по нему двух ударных волн 2 1

(со скоростью G₁ ) и 2 ₂ (со скоростью G ₂) (Рис. 1). Волна 2 1 вызовет только увеличение антиплоского сдвига, и, следовательно, за ней (см. область I) функция у ( r , t ) останется нулевой, поскольку сюда еще не пришло граничное возмущение. В области II окружные перемещения отсутствуют ( у = у II = 0), так как ударная волна 2 1 является плоскополяризованной, и на ней выполняются условия (9). Окружные перемещения появятся после прохождения нейтральной ударной волны 2 2 , то есть только в области III, где u = u ¹¹¹ * 0

"^----11—►   и у = уш * 0 .

II

В области деформирования II представим перемещения u ^II ( r , t )

Рис. 1. Схема распространения в форме лучевого ряда ударных волн

да

u ⁿ( r , t ) = u I ( r ) - ^ K j

j =i

⁽ t ^- t i ) j

d t^j

Jjdk

^{1 J} G i ( ^ ).

Для скорости G 1 ударной волны 2 1 , следуя зависимости (10), получаем

G = c ( 1 + х ( u ,I r ) 4 ( 5 - 10 Z + 10 Z ² - 5 Z 3 + Z 4 +

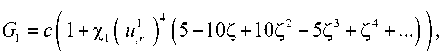
Z = K ( cu ,I r )

Коэффициенты к j лучевого ряда (13) являются разрывами производных функции u ( r , t ) на поверхности разрывов 2 ₁ . С целью их вычисления нужно уравнение движения, а в данном случае это будет соответствующим образом переписанное уравнение (4) 4 , продифференцировать необходимое число раз по времени и записать в разрывах на 2 ₁ . Кроме этого потребуются геометрические и кинематические условия совместности разрывов [25–27], которые в прямоугольной системе координат имеют вид:

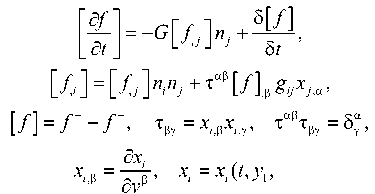
[ f i ] = [ f j ] ⁿⁿ ■ T^{a [} f ^] , _p g y x j.

авт = Xa

Здесь: ya (a = 1,2) — поверхностные координаты на поверхности разрывов 2(t); f (t, x1, x2, x3) — функция, терпящая разрыв на 2(t); gij, tPy — компоненты пространственного и поверхностного метрических тензоров, греческие индексы принимают значения 1, 2 (такими индексами после запятой обозначена операция ковариантного дифференцирования по соответствующей поверхностной координате); 5/5t — операция 5 -дифференцирования по времени функции на движущейся поверхности S(t). Условия совместности (15) записаны для производных только первого порядка. Их обобщение на случай, когда закон движения поверхности разрывов S(t) изначально задается не в прямоугольной системе координат, как в (15)4, а в произвольной криволинейной, было получено в [27]. При [f ] = 0 из (15) получаются классические условия совместности Адамара, которые вместе с динамическими условиями совместности разрывов (7) служат выполнению первого шага на рекуррентном пути вычисления коэффициентов лучевого ряда (13). Следующий шаг связан с записью в разрывах на Х1(t) уравнения движения (4)4 при условии, что v = 0. На последующих шагах данное уравнение необходимо продифференцировать по времени соответствующее число раз и результат записать в разрывах. Выражение, завершающее такие рекуррентные действия, здесь не приводится из-за его громоздкости. Заметим, что его можно представить в форме:

8 n ^-1к

M n к n + N n -i         — Y n -2 = 0.                                   (16)

5 t

В (16) n — натуральное число; N -1 = N ₀ = 0, Y_{- 2} =Y _1 = Y ₀ = 0, N 1 = N ₂ = ..., M ₂ = M 3 = ..., но M 1 * M ₂. При этом M k , N _k , Y k зависят от предварительных деформаций, к j (при этом j <  к ) и 5 -производных функций, заданных на движущейся поверхности 2 ( t ). При n = 1 равенство (16) требует, чтобы M ₁ = 0 , поскольку именно из этого условия вычисляется скорость распространения поверхности разрывов. Для поверхностей разрывов ускорений (слабых волн) условие имеет вид: M 1 = M ₂, и тогда (16) распадается на рекуррентную систему обыкновенных дифференциальных уравнений (уравнения затухания).

Но для обсуждаемых здесь ударных волн этот классический случай исключен, так как M 1 * M ₂. Согласно (16) возможно только считать, что

5к . ,

— = bk (к1, К2 , ..., кn +1), 5t либо наоборот, рекуррентно найти

Следовательно, условия совместности разрывов позволяют на каждом шаге расчетов связать к _{n + 1} с 5 ⁿ к 1 /5 t n .

Такая связь законов сохранения и кинематических условий совместности разрывов дала возможность (см. [19, 20]) преодолеть отмеченную особенность в построении приближенных решений в областях, находящихся за ударными волнами. Интенсивность ударной волны при этом, а это была к1, представлялась степенным рядом к1

”

= Z  Ykt , к=0 к!

5 ^к к

^{Y к} = 5 t ^k

.

t =0

Использование в ряде (19) 5 -производных по времени диктуется тем, что к 1 ( t ) задается на движущейся поверхности S 1 ( t ). Постоянные у _к подлежат определению через выполнение краевых и начальных условий ударного нагружения. Как правило, из таких условий находятся к _{к + 1} при t = 0 ; тогда зависимости вида (17) и (18) служат рекуррентными условиями для вычисления у _к . В случае к = 1, то есть на первом шаге вычислений, из (17) и (18) следует:

5к 1

"57

5 4, J

= 2 и ,r ^к 2 X 1 ^{+ к} 1 1 ^-

С , а 3       , ^{10 U}Г ^к 2 X 1 Y 2 ^{f 15u} 3 X 1

---¹⁰ cU , r^u , rr ^X 1 + ------------- I + ^к 1 I --------- 2 r ^{, ,}              c                  2 r

^{- 15и} 2r^u , rr ^X 1 ⁺

15 и 2 к 2 X 1

За поверхностью разрывов круговой поляризации S ₂( t )— в области деформирования III (Рис. 1) — лучевые ряды для искомых функций и ¹¹¹ ( г , t ) и v™( г , t ) запишем так:

со

(t—tY j ! ,

и ^ш( r , t ) = и ^п( r , t )|     - ^ to j

1 t=t2- , j = 1

, ,     4     ( t — t 2) j

V( r, t) = —En,- j=1

п

d ^j v " d t⁷

® j

t = t 2

8 ^j u

d

r t 2 = J r0

d 0

G 2 ( 0 ).

Скорость G ₂ ( t ) распространения данной нейтральной ударной волны найдем с помощью зависимости (11)

G 2 = c ( 1 + ^X 1 u¹ r|t =^ + ... ) .

Для того чтобы записать на S ₂( t ) соотношения, аналогичные (17) и (18), необходимо уравнения движения (4)₃ и (4)₄ продифференцировать по времени требуемое число раз и результат записать в разрывах на этой ударной волне. Следует иметь в виду, что интенсивности разрывов ю 1 и n 1 связаны на нейтральной ударной волне S ₂( t ) условием [ m ] = 0 . Из-за этого результат обозначенных вычислений представим в обобщенной форме

5n j

— = ? 7 ⁽ П 1 , П 2 , ..., П j +1 ), 5 t

5to j

. = » j ( n_PП 2 , ..., n j +1 ), 5 t

или наоборот

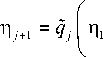
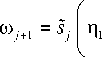
8П 1

5 t ’

8П 1

5 t ’

j ! )

, 5 t j J ,

, 5 t j J .

Для дальнейшего достаточно будет в разложениях (21) ограничиться второй степенью по времени.

Тогда зависимости (23) и (24) принимают следующую форму:

5П 1 = ^и >2 X 1 + ^{2 и} , , n^X x 5 1      2           c

I ³^з

— П 1 c l — + 2 u , u rr X 1 1 +

V 2 r           J

^+K 1

² u ,³ r П 2 Х 1   б и Г л^

c

^{3 u} XX:

c ²

u

¹ + 3 П 1 и rh l — 2 U rr ,        1 r ■

14 r 2 и , r X 1

5 c

4 14 1 ^u ,4 X 1

1 Y

— +

2 JJ

^+K 2

c ²

³ П 1 Х 1 ^и ,,

c

1^-T¹- П 2 П 2 ( ^{6 u} ,4 X 1 ^{— 1}

5c u,r + 2 и, rr (32 и 4rX1 — 1)

³ П 1^К2 ^и , r X 1/, „_Q 4   \

—С У"— ^{( 2 — 79 и} , r ^X 1 )

+ ...,

r ²П 1 П 2 ₊ r n 2 f 13 +    1   ) + ^{r2 и}2 n 2 ^K 2 X 1

си , r и , r V 10   2 и ,⁴ _r x 1 J c ²

+K

П 2 K 2 —— ( — 12 — 77 и 4 X 1 + 1601 и 8 X 2 ) + П 1 П 2 —tt ( - 1 - 3 и 4 X 1 + 7 и r X 2 ) +

5 c ⁴ u ^{4                 ,                ,}                  5 c ³ u ^{3             ,           ,}

+n 2

r (25 + 7 и ,⁴ r X 1 + 14 и T x 2 + 41 и ,1 , 2 x 3 ) 2 r ² и , rr ( — 6 — 131и 4 X 1 + 458 и ^ x 2 )

5 c 2 и T X 1

5 c ² u ⁴

(         4 r ² ,       , x .        r ² ,           .               „ A

П 1 П₂ туг ( 1 ^— u,r X i ) ⁺ П 1 ^K 2 ... ( 6 ^{— 6i} u,r X i ^{+ 2} 2 4 X i ) ⁺

5 c ² u ^{2        ,}                 5 c ³ u ^{3            ,              ,}

^+K i

+П 2

r (2 — u 4 X i + u 8 X i² ) 2 r ² u , rr (3 + 2 u 4 X i + 8 u Г X 2 )

+ ...,

cu , r X i

Ю 1

—

5 cu _,

22 ^r Hi ,

....

cu _{, r}

Необходимо иметь в виду, что производные функции u ( r , t ) в (25) вычисляются при t = t ₂, так же, как в (20) — при t = t _i.

Для ni по аналогии с (19) принимаем разложение skn

П =УА p t^k ,  р^-А х .

1    k   kk k!                   -t k=0                                 t=0

Поскольку to _i и п _х связаны на S ₂( t ) условием [ m ] = 0 (последнее соотношение из (25)), то to _i также представляется степенным рядом по времени. Зависимости (13) и (21), таким образом, тоже приобретают форму степенного ряда. Рекуррентным степенным рядом представляются с помощью (14) и (22) и зависимости для t _i и t ₂. Неизвестные постоянные у _k и P _k находятся из граничных условий, для чего в переписанных в соответствующем виде выражениях (21) следует положить t ₂ = 0 (или, что то же самое, — r = r ₀) и сравнить с (12). Зависимости (17) и (23) позволяют рекуррентно пересчитать у _k и P _k через параметры граничного воздействия u ₀ и у _k . Если всюду ограничиться только слагаемыми, содержащими время до второй степени, то можно получить:

A A

|c P i + u , r ( r , ) Х/PM ⁽ i — 29 u ,⁴ r ( r 0 ) | + 2 r        ’             3 c ³       V 3 ’       )

У ^{( r} , t ) = ^—

P i

^— t - 2

+ X i

—

+ ...

х ( t — t ₂) — ( в ₂ + ...)( t — t ₂) ² + ...,

V

—

V

X i ^ur ^{( r} 0 ) | ^^ 2 ^{— P} i ^{( 2} cu rr ^{( r} 0 ) ^{— 3} Y i ^{— 2} Y 2 V c V               r c

/ у

(

r 2 P i

I   ,8k.

u ( r , t ) = u ( r ) — I Y i + t i ■ —-V - 1

3 c P,

2 r

^{r 2 u} , r ⁽ r iM^ X i Y i

3 c ³

^P i ^— t 2

+—V

22 r P 2

—

⁺ ... I ⁽ t ^— t i ) ^{— ( Y} 2 ⁺ ... ⁾⁽ t ^— t i^{)2 +} t =0       )

29 r ² u ,⁵ r ( r 0 ) P 2 P 2 X 2 Y i               A

9 c ³

^— u ^r ^{( r} 0 ) X i ⁽ 2^ ^{+ P} i ⁽ — ⁺ 2 ^Y 2 ^{— 2} cu , rr ^{( r} 0 ) ^{A A} V c V r c                ))

2 cu , r ( r ) ( i + X i u 4 ( r ) + 6 X i u ,2 r ( r ) Y 2 / c 2 )

r ² P i P 2 , 539 r P 2 Y i , 4 r ² P i P 2 Y i _|D2 2 r ² Y i

9 u _{, r} ( r ₀) cu _{, r} ( r ₀) 27 cu _, ² _r ( r ₀) 3 c ² u _, ² _r ( r ₀)      ¹ c ³ u _, ³ _r ( r ₀)

5 r P 2

—

50 r P 2 Y i

6 u Г ( r 0 ) X i 9 cu 6 ( - 0 ) X i

—

P 2 r ² Y i X 2

, r 0       3 c 3

—u2(r )-Ад

, r 0     9 c 2

^{298 c 2 u} , rr ^{( r} 0 ) ^—

P 2 r ² Y i X_: c ³ 4037 y ₂ a

9 у

—

Л

+ ...

— х ( t — 1 2 ) —

( y 2 ^— c ² u , rr ^{( r} 0 ) )

^ ^{( 8 c 2 u} , rr ^{( r} 0 ) ^— 629^ 2-

—

I 77     rR.

+ ur ( r 0 ) X i r P i I — P i + -b-V 27       c

56 P 2 Y i +P i ^{( 30} 29^Y£ + i5 Y 2 V 3 r

х ( t — t ₂) ² + ...

—

Здесь

t i =

______________________ r ^— r o ______________________ c ( ¹ + 5 X i uU^r 0 ) ( uUr o ) + ² Y i I^е ( Y i c ^— u , r ⁽ r o ) ) ) )

-

t 2

c ( ^{1 +} X 1 u ^{2 ( r} 0 ) ( u ^{2 ( r} 0 ) ^{+ 2} Y 1 / c ( ³ Y 1 / c ^{— 2} u , r ^{( r} 0 ) ) ) )

—

5k

5 X 1 ■

5 t

■ u ,² r ^{( r} o ) ( ² Y 1 / c ^— u , r ^{( r} 0 ) ) ( ^{r — r} 0 ) ²

t =0

c ³ ( ¹ + 5 X 1 u ,² r ^{( r} 0 ) ( u ^{2 ( r} 0 ) ^{+ 2} Y 1 I^е ( Y 1 / c ^— u , r ^{( r} 0 ) ) ) )

- 5k

2 X 1 ■

5 t

■ u ^{2 ( r} 0 ) ( ³ Y 1 c ^— u , r ^{( r} 0 ) ) ( r ^— г ) ² t =0

c ³ ( ^{1 +} X 1 u ^{2 ( r} 0 ) ( u ^{2 ( r} 0 ) ^{+ 2} Y 1 /с ( ³ Y 1 / c ^{— 2} u , r ^{( r} 0 ) ) ) )

Коэффициенты лучевых рядов в (26), определенные из начально-краевых условий, принимают значения:

Y 1 = 1         +...,

2 cu , r ^{( r} 0 )

Y 2 = c ² u , rr ⁽ r O ⁺ ."> Р 1 =-V 1 , Т =-V 2 .

• 4.    Применение лучевых рядов к выделению разрывов в разностной схеме

Полученное в предыдущем разделе с помощью модифицированного лучевого метода решение может считаться справедливым только для малых послеударных времен. Обусловлено это тем, что в выражениях (20), (25), описывающих эволюцию интенсивности разрывов, и в (26), представляющих непосредственно движение точек сплошной среды после прохождения через них ударной волны, не учитывается нелинейный характер затухания. Поэтому применение (26) для идентификации кинематики точек среды ограничивается далее некоторым малым значением времени — tq. При t > t в расчетную схему включается процедура удовлетворения уравнений динамики в той части области, где уже прошла ударная волна круговой поляризации, и где возможно записать в разностном виде вторые производные по времени функций у(r, t) и u (r, t). Здесь необходимо проинтегрировать уравнение движения и, положив существование близ фронта волны лучевых разложений, но только с неизвестными коэффициентами в лучевых рядах, срастить эти два решения, варьируя коэффициенты лучевых разложений. Параметр tq в определенной степени произволен, однако не может превышать значения, при котором линейное приближение скорости затухания волны даст падение до нуля ее интенсивности. Для реализации означенного подхода построен специальный алгоритм.

Область t >  t q и r е [ r ₀, r ₂] покрывается равномерной

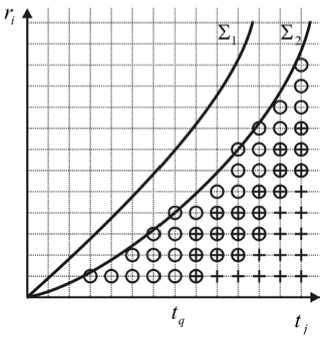
Рис. 2. Маркировка узлов пространственновременной сетки

сеткой с шагами At по времени и Ar по пространственной координате. Пространственные производные функций ^(r, t) и u (r, t) записываются с использованием центрально-разностной аппроксимации, для записи производных по времени применяется чисто неявная разностная схема.

Положения фронтов поверхностей разрывов деформаций в момент времени tj обозначим 21 (tj) и 22 (tj). Таким образом, в текущий момент времени tj для точек r е [ r0,22 (tj—2)) (именно в этой области возможна разностная запись вторых производных по времени у/ и и) исходному уравнению движения ставится в соответствие его дискретный аналог в виде системы нелинейных алгебраических уравнений, замкнутой краевыми условиями (в узлах, обозначенных

« + » и «®» на Рис. 2). Одно из них — условие (12) на нагружаемой границе, второе — перемещение, вычисленное с помощью приближенного аналитического решения в ближайшем к границе 22 (tj—2) узле r>2222 ( tj—2 ) .

Система уравнений решается численно, таким образом, находится поле перемещений за второй ударной волной. Исключение составляет прифронтовая зона, где запись дискретизированного уравнения движения невозможна (в узлах, обозначенных символом « О » на Рис. 2). Предполагается, что в этой зоне функции у(r, t) и и(r, t) также описываются лучевыми рядами в форме (13), (21) с той лишь разницей, что значения дельта-производных аппроксимируются конечно-разностными выражениями, а коэффициенты лучевых рядов являются неизвестными априори и подлежат идентификации. Возможность для такой идентификации дает выполнение естественного условия гладкости решения на всей области за второй ударной волной. В силу этого относительно указанных параметров решается задача минимизации невязки лучевого разложения и перемещений, полученных интегрированием уравнения динамики, в нескольких соседних узлах вблизи границы Σ2( tj-2) (обозначены символом «⊕» на Рис. 2). Этим завершается текущий шаг алгоритма по времени: теперь во всей области за ударной волной круговой поляризации определены перемещения точек среды и идентифицированы значения величин разрывов.

Указанный алгоритм реализован программно в среде Mathematica 10.4.1. Его работа протестирована на решении задачи динамического нагружения резиноподобного материала со свойствами с = 55 м/с, χ ₁ = 200 , µ = 2,6 ⋅ 10 ⁶ Па. Геометрические размеры слоя составляли: r ₀ = 0,01 м, R = 0,02 м. Параметры движения внутренней границы равнялись: u ₀ = 0,001 м, ψ ₁ = 20 π , ψ ₂ = 300 π . На рисунках 3, 4 и 5 представлены эпюры углового смещения ψ , нормированной компоненты тензора напряжений Коши-Эйлера σ_{ϕ z} µ , а также нормированной интенсивности η ₁ ψ ₁ соответственно.

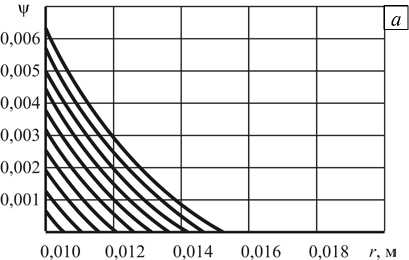
Рис. 3. Эпюры углового смещения ψ ( а ) и нормированного касательного напряжения ( б ) в различные моменты времени (шаг по времени составлял 10 ^{- 5} с)

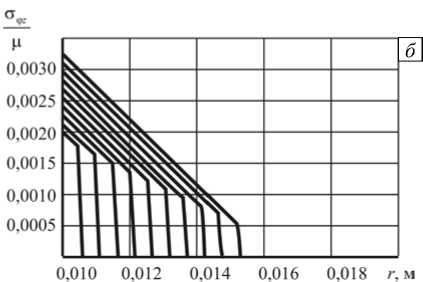
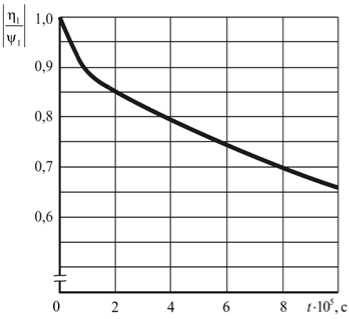
Рис. 5. Эволюция нормированной интенсивности разрыва

• 5.    Выводы

На основании приближенного метода построения лучевых разложений решений за поверхностями разрывов и специального алгоритма решена задача выделения разрывов, распространяющихся в несжимаемом упругом цилиндрическом слое, подвергнутом предварительному деформированию. Созданные деформации оказывают существенное влияние на скорости ударных волн: чем они больше, тем дальше с течением времени отстоят друг от друга соответствующие поверхности разрывов. При этом предположений о малости деформаций или интенсивностей разрывов не делалось, что позволяет использовать полученные решения для процессов с большими интенсивностями прикладываемых ударных нагрузок.

Работа выполнена при частичной финансовой поддержке РФФИ (проект № 14-01-00292).