О вынужденных колебаниях конечной амплитуды в многослойной ультразвуковой камере

Как известно, применение ультразвуковых волн конечной амплитуды получило очень большое применение в различных областях науки и техники (см., например, [1]). В частности, широко применяются всевозможные ультразвуковые камеры, в которых принудительно создаются стоячие акустические волны конечной амплитуды. Эти камеры могут представлять собой достаточно сложные акустические волноводы, в которых, как правило, ограничиваются расчетом акустических полей в линейном приближении (см., например, [2–4]). На практике же может возникнуть необходимость расчета волновых характеристик с учетом нелинейных эффектов. Наиболее простыми в этом смысле являются области, в которых акустические поля описываются в рамках плоского движения (зависимость только от одной переменной). В настоящее время известны решения для поля стоячих волн в простейших случаях узких однородных ограниченных труб для собственных и вынужденных колебаний [5–7]. Обычно в таких случаях пользуются уравнениями гидродинамики в лагранжевых координатах. Исходная задача нелинейной акустики решается, как правило, методом последовательных приближений. В этом случае удается решить задачу аналитически.

В настоящей работе рассматривается ограниченная труба, заполненная жидкостью, для которой справедливо предположение о плоском движении, при этом плотность жидкости и скорость звука в ней носят плоскослоистый характер. Априорно очевидно, что в общем случае такая задача должна решаться численно. Поэтому после постановки проблемы и формулирования ее общего решения на примерах приводятся численные решения.

ПОСТАНОВКА ЗАДАЧИ

Пусть задана труба конечной длины L , с одной стороны которой при a = 0 установлен поршень, осуществляющий вынужденные гармонические колебания частотой to , а со второй стороны при a = L задано импедансное краевое условие, в частности граница с воздухом. Труба заполнена жидкостью переменной плотности р ₀( a ) и скорости звука c ₀ ( a ), относящихся к равновесному состоянию среды. Для акустических колебаний справедливо допущение о плоском движении, т. е. зависимость от одной переменной. Независимая переменная a рассматривается в лагранжевых координатах и привязана к конкретным частицам среды, находящимся в равновесном положении в точках а е [0, L ]. Это связано с тем, что при учете нелинейных эффектов границы уже нельзя полагать неподвижными, они колеблются вместе с акустической волной, а это и учитывает система координат Лагранжа, связывающая акустические величины не с точкой в пространстве как в координатах Эйлера, а с конкретной частицей среды, вернее, с точкой пространства, где эта частица находится в равновесном состоянии.

Функции р ₀( a ) и c ₀( a ) могут либо быть по крайней мере однажды дифференцируемыми, либо иметь разрывы первого рода, в частности быть кусочно-постоянными.

Необходимо рассчитать величины акустического поля с учетом нелинейных эффектов по крайней мере во втором приближении.

РЕШЕНИЕ ЗАДАЧИ В ОБЩЕМ ВИДЕ

Наиболее распространенным методом решения задач для акустических волн конечной амплитуды является метод последовательных приближений, когда некий параметр акустического поля q представляется в виде ряда по степеням некоего малого параметра, которым обычно выступает число

Маха M = -, где v — акустическая колебательная скорость, c — скорость звука (для акустического давления в воде 1 атм = 1.0132 х 10⁵ Па число Маха M = 0.0004 [8, с. 267]):

q = q 0 + j M + q 2 M ² + ... + q n M" + ••• =

= q 0 + q + q 2 + -+ < n + -^,                 (1)

q , = q , M l , l = 1,2,...,.                        (2)

а (6) разложить в ряд Тейлора

p - p ₀ = M р ₁ + M ² p ₂ + M ³ р ₃ + ... =

d p

. 1 d² p

2 d Р ²

1 d³ Р +

6 d р ³

( мр + m ² р ₂ + m ³ р ₃ + ...) +

( Mp₁ + M ² р ₂ + M ³ р ₃ + ...)² +

Р = Р 0

Р = Р 0

( Mp₁ + M ² р ₂ + M ³ р ₃ + ...)³ + ...

В (1) для удобства сепарирования величин различной степени малости явно выделены степени малого параметра M .

Далее рассмотрим в лагранжевых координатах одномерную систему уравнений гидродинамики для идеальной жидкости [7, с. 414]:

— уравнение движения

и рассмотреть величины одинакового порядка малости, а также учесть переменный характер p ₀ ( а ) и c ₀( а ), то после несложных, но достаточно громоздких выкладок можно получить рекурсивную систему неоднородных волновых уравнений, например, для акустического давления с правыми частями, в которых фигурируют только комбинации из предыдущих решений:

рЛ„ + Р а = 0;                   ⁽³⁾

— уравнение неразрывности (закон сохранения масс)

a

Р 0 ^- Р

Р

— эмпирическое уравнение состояния (уравнение Тэта) для жидкостей [5, с. 7]

Р = P ,

Y

5 - 1 . V ^{Р 0} J

= Р ⁽ Р ),

d 2 р ,		1	d P 0 d P l	1    d 2 Pl =
d а 2    р 0( а = L l ( P 1 , P 2,. Л dp Обозначим: A = d p			) d а d а   c 02( а ) d t2 ., pi - 1); 1 = 1 , 2 ,... 1                 ( = 2zW где c 0( а ) C o ( а ) P = P 0     0V/		(8) — ско-
рость B ( а ) =	зв 1 d2 p 2 d p2	ка    в    равн ; C ( а ) = ^Т 7 6 d p p = p 0                r		овесной . P = P 0	среде;

или, обращая (5),

Р = Р ( Р ).                         (6)

В (3-6) введены обозначения: а — переменная в лагранжевых координатах; ^ — смещение частицы относительно положения равновесия; p — суммарная плотность; Р — избыточное давление жидкости; p ₀ и P, — равновесные значения последних в отсутствие акустического поля; у — эмпирические константы (для жидкостей см. таблицу [9, с. 8]).

Если в уравнения (3), (4), (6) подставить величины

L , ( Р ₁, Р ₂,..., Р , - 1 )— функции, характеризующие влияние волн низших гармоник как внешних источников возмущения поля. Приведем первые три функции L l , l = 1,2,3:

L ^ 0,

A\ ^{Э 2} ( Р ²)

^{L 2} = ⁽ B "  5 )

p = p ₀ + M р ₁ + M ² p ₂ + M ³ p ₃ + ... =

= ^Р 0 ^{+ Р} 1 ^{+ Р} 2 ^{+ Р} 3 ⁺ — ;

£ = М ^ + M ^ 2 + M ^р + ... = ^ 1 + ^ 2 + ^ 3 + -,

L ₃ = - 6 Cp₁ p² + 4 Bp p ₂ - 2 ^{Ap1( Ap 2 +} B ^{( P 1} ) t ) - Р ₀

• ^- Р 0 ^AP 1^{( Ap} 2 ^{+ В (} P 1 ^{2 )} t ') - ^{3 C}P 1 ^{2 p} 1 ⁺

\ A"Pl ( Ap ₂ + BP 1²)

• ^{+ 2} B ⁽ P 2 Р 1 ⁺ Р 1 P 2 )---

• Р0

AP 1 ( AP 2 + B ( P 1 ²) . ")

Р ₀

• -    Ap¹; ( - 6 A ³ p , ^p ,2 + ² P 0 ^Ap ,⁽ Ap 2 + B ⁽ p ,2 ) ;) ) -

• P02

• -    P ¹ ( 3 ^{A 3} p , ² p + P 0^{( A}P 2 + Bp , ²) ) .            (11)

Точки над функциями в (11) означают дифференцирование по времени.

Отметим, что выражения для L ₁ и L ₂ приведены в [7, с. 416]. Кроме того, из (10, 11) видно, что L l должно содержать частоты вплоть до l to , где to — частота колебаний первой гармоники.

тт 1 d p др,

Член         ^{0 l} в уравнении (8) появляется

P0(a) da дa в процессе получения волнового уравнения в данном случае для акустического давления. При этом приходится дифференцировать уравнение движения (3) по переменной a.

Рассмотренные выше уравнения (3–5), (8) справедливы для идеальной жидкости без учета диссипативных эффектов вязкости. С учетом вязкости уравнение (8) приобретает сложный вид, и его упрощают простой диссипативной добавкой [6, с. 130]. В дальнейших рассуждениях диссипативный член учитываться явно не будет, однако при получении решений системы неоднородных уравнений (8) будут использоваться установившиеся вынужденные колебания.

Кроме того, отметим, что метод последовательных приближений правомерен в случае, когда акустическое число Рейнольдса Re невелико [10, с. 203]:

Re = v-^, bto где v0 — амплитуда колебательной скорости; b — диссипативный коэффициент.

Поставим граничные условия при а = 0 и а = L. На границе а = 0 источником вынужденных колебаний служит плоский поршень. Полагая, что поршень на границе осуществляет линейные колебания, получаем, что на поршне присутствует только первая амплитуда колебательной скорости v (0, t) = v,(0, t), v 2(0, t) = v3(0, t) = v4(0, t) =... = 0.

Поскольку в нелинейной акустике неправомерно использование временного фактора e - ^{i to t} , примем временной фактор в виде cos to t , либо sin to t . Из уравнения (3) имеем

P0£« + Pa = P0 v + Pa = 0, откуда получаем

1    д p   = д v

P 0^{( a} ) ^{д a} _a = ₀       ^д t a = 0'

Или, принимая скорость движения поршня на границе a = 0 как v = - v 0sin tot,                   (13)

получаем систему граничных условий при a = 0 в следующем виде:

^д p , д a

= toP 0 (0) v ₀ cos to t , a = 0

^д p 2     = ^д p 3

^{д a} a = 0     ^{д a} a = 0

Краевое условие на конце a = L при отсутствии сторонних сил может быть принято в виде однородного условия Дирихле, либо Неймана, либо смешанного краевого условия (импедансное краевое условие). Поскольку выбор условия не носит принципиального характера, примем, что жидкость граничит с воздухом, а это соответствует тому, что имеет место однородное условие Дирихле p, la = L = p2 la = L = ". = 0.               (16)

Поставим задачу математически. Систему (8) будем решать до второго приближения включительно. Для первой гармоники волновое уравнение запишется в виде д 2 p, -   1   dP0 дp, -   1   д 2 p, = 0

д a ²     P ₀( a ) d a д a c ₀²( a ) д t ²

где фигурируют соответствующие значения невозмущенной скорости звука c0 и плотности сре ды P0. Краевые условия имеют вид:

^д p , д a

= toP 0 (0) v ₀ cos to t , a = 0

p , l a = L = 0.

Для второй гармоники волновое уравнение с учетом (10) имеет вид д2 p2 1 dP0 дp2 1 д2 p2

"d^ P to I P I P C 0>) "t^ "

= 1d 2 P -      1      ) ^{д 2} ( p , ²)

2d p²_p = _p 0 ^c 0^{4( a} ) P 0^{( a} ) ^д t²

с нулевыми краевыми условиями дР 2

^д a a = 0

= ⁰ , Р 2I a = L

= 0.

Правую часть (19) для идеальной жидкости в случае кусочно-постоянной плотности можно привести к виду [7, с. 417]

где y 1 , y ₂ — решения задачи (23), удовлетворяющие краевым условиям (26) соответственно при a = 0 и a = L ; k = to I c ₀( a ); w ( to , a ) — вронскиан решений y 1 , y ₂

' 1 d² р      -      1      ) ^{д 2} ( Р ' ² )

^{2 d} p²_p = _p 0 c 0 ⁴ р 0⁽ а )     д t²

. x - z x d y ₂( a ) d y ( a ) _ . .

w ( f X ^a ) = У 1 ^{( a} )—---- — y 2 ^{( a} ).       ⁽³⁰⁾

d a     d a

1 1

² c 0 ^р 0

( у + 1)

^{д 2} ( Р -2 ) д t²

После нахождения решения (27) задачи (25), (26) решается задача (19), (20) с правой частью (10); при этом L ₂ с учетом (10), (22) и (27) рассчитывается следующим образом:

где, например, для воды у = 6.1 [9, с. 8].

Предполагая наличие потерь в системе, будем рассматривать установившиеся колебания. Решение будем искать в виде

L ₂( a ) ) cos2 to t =

p 1 ( а , t ) = P ( a )cos to t .              (22)

_{v v} ^c 0 ^{4 ( a} ) P 0^{( a} ) x cos 2 to t .

- B ( a ) to ⁴ p ²(0) v ² G ²( a ,0, to ) x

J                       J

Для (17), (18) имеем одномерную краевую задачу dP--^М dP + k 2( a) P1 = 0, d a    p 0( a) d a da

Решение ищем в виде p 2( a, t) = P2( a )cos2tot,               (32)

что приводит к краевой задаче dP da

= ^toP 0⁽⁰⁾ v 0 ,

P l ,= 0.

¹ l a = L

a = 0

d² P ₂( a ) d a ²

--^M ^d PM + (2 k ( a ))² P ( a ) p ₀( a ) d a    д a               ²

Известно, что задача (23), (24) сводится к следующей [11, с. 21, 22]:

= L 2 ( a );

d² P d a ²

1   d p 0 dP 1

p ₀( a ) d a d a

+ k ²( a ) P 1 = top ₀(0) v ₀ 8 ( a ), (25)

d P ₂ da

= 0;

a = 0

^P .| a = l = °-

d P d a

= 0, a=0

P l ,= 0.

¹ l a = L

где L ₂( a ) дано в выражении (31) во внешних круглых скобках; k ( a ) = to I c ₀( a ).

Решение (33), (34) находится из выражения [12]

Решением задачи (25), (26) является функция

P ( a ) = top 0 (0) v 0 G ( a ,0, to ),            (27)

где G ( a, ^ , to ) — функция Грина задачи (25), (26), когда правая часть в (25) равна 8 ( a - § ). Учитывая, что уравнение (25) можно переписать в самосопряженном виде, применительно к функции Грина получаем уравнение

. . d ( 1 dG(a£,to)) ,2,.

Pa(ah--.       + k (a)G(a£,to) = da ^ p0 (a)    da

= 8(a - 5).(28)

Используя технику, изложенную в работе [12, с. 572], можно показать, что в этом случае имеет место равенство

G ( a , 5 , to ) =

1 У 1 ( a ) y ₂( ^ ),    ^a <  ^ ;

w( to Л ) 1 y( £ ) y ₂( a ),   ^a > ^

P 2 ( a ) = J G ( a , ^ ,2 to ) L 2 ( ^ )d ^ = 0

= У 2 ( a )            t 2 ( ^ )d ^ +

^J0 w (2 to , ^ )

+ У 1 ( a ) 1 4^ L . ( « )d « ).         (3 ⁵ )

a w (2 to , ^ )

где

G ( a , ^ ,2 to ) =

1       У1( a ) У 2(^ ), w (2to, ^) 1 У1(§) y 2( a X a < ^, a > ^;

y ₁ , y ₂ — решения однородного уравнения (33) с краевыми условиями (34) соответственно при a = 0 и a = L ; w (2 to , ^ ) — вронскиан решений y 1

и у ₂. Если функция равновесной плотности р ₀ ( а ) непрерывна на всем интервале а е [0, L ], то вронскиан применительно к уравнениям (23) и (33) может быть вычислен по формуле [13, с. 76]

_J_d £ 0.

w ( to , а ) = w ( to , a ₀)        J р ₀( a ■) d a'

_                   , Г e° ⁰

w (2 to , а ) = w (2 to , a ₀)

полнять условия сшивки на границах, которые заключаются в непрерывности давления и нормальных к границе компонент колебательной скорости, а именно для колебательных скоростей и акустических давлений на границе а , сред i и i + 1 ( i = 1, n - 1) справедливы равенства

Р\_а = Р |_а •             ⁽³⁹⁾

^{1 а}i -            ^{1 a}i +

Здесь а ₀ — некоторая точка, в частности можно положить а ₀ = 0 .

Таким образом, выше были найдены амплитуды первых двух гармоник рассматриваемой задачи в виде (22) и (32) с соответствующими амплитудами стоячих волн в виде (27) и (35) в случае плавного изменения равновесных плотности и скорости звука жидкой среды в трубе. Отметим однако, что практически более реалистичной ситуацией является кусочно-постоянный характер изменения этих характеристик среды. Получим решение задачи применительно к этому случаю.

Здесь ± говорит о рассмотрении величин слева от границы а , (знак -) и справа от границы а , (знак +). Из линейности (39) и из (1) получаем аналогичные равенства для всех гармоник l = 1,2,3,...

v iL^ = ^v i L^,

P i L^ = P iL^ •

Для гармонического сигнала условие (40) с учетом (3) преобразуется

РЕШЕНИЕ ЗАДАЧИ В СЛУЧАЕ МНОГОСЛОЙНОЙ ЖИДКОСТИ С КУСОЧНО-ПОСТОЯННЫМИ ПАРАМЕТРАМИ

Пусть жидкость в трубе состоит из n смежных слоев с кусочно-постоянными значениями равновесных плотности и скорости звука. Пусть далее краевые условия (14-16) на концах трубы остаются неизменными.

Учтем специфику рассматриваемой задачи, заключающуюся в кусочно-постоянном характере изменения значений равновесной плотности и скорости звука внутри каждого 1 -го слоя модели. Внутри интервалов постоянства равновесных скорости и плотности в соответствующих уравнениях (25) и (33) составляющая дифференциального оператора

1 dPo d _ 0 р 0( а) d а d а аннулируется, а остается только соответственно дифференциальный оператор

2,7

F, = -у + k?,     i = 1, n ,           (37)

d а либо

F, = d^ + (2 k , )²,      i = b n ,        (38)

d а где ki = to I c0i; c0i — равновесная скорость звука в i-м слое.

На каждой i -й границе раздела необходимо вы-

d p_l I d а P 0 i

_ d p_l I d а _a -       ^р 0 i + 1

а +

.

Здесь р ₀ i — равновесное значение плотности в 1 -м слое.

Отметим, что условия сшивки (41), (42) совпадают с аналогичными граничными условиями, принятыми в линейной акустике.

Используя выражение (21), перепишем уравнения (25) и (33) краевых задач (25), (26) и (33), (34) на каждом интервале постоянства плотности и скорости звука в виде

d²    P 1 ( а ) 1         P 1 ( а ) 1

т 1 „ , , r + k i i Л d a ² P ₂ ( a ) P ₂ ( a )

а е [ l , - 1 , l , ],    i = 1, n .

Здесь

toр 01 V 0 ^ ( a )

k4.

—^L e G ²( a ,0, to ) р 0 ,

а = 2 р 012 v 0 2;		(44)
e = ( у , + 1) 1         2      ,	1 = 1, n .	(45)

Решения у 1 , y ₂ и у 1 , у ₂, фигурирующие соответственно в функциях Грина (29) и (36), в этом случае необходимо конструировать следующим образом. Решения у 1 , у 1 удовлетворяют в i -м слое соответственно дифференциальному уравнению F , ( У 1 ( а )) = 0 для первой гармоники и F , ( у 1 ( а )) = 0 для второй, а также граничному условию при а = 0 (26) и (34) соответственно; на границах ме-

жду слоями решение удовлетворяет условиям сшивки (41), (42). Решения у₂, у ₂ строятся аналогично, но удовлетворяют граничному условию при a = L (26) или (34) соответственно.

Найдем выражение для определения вронскиана в случае кусочно-постоянного поведения равновесной плотности. Как видно из (36), вронскиан решений у ₁, у ₂ и у ₁, у ₂ на каждом интервале a е [ a i _ч, a i ] есть величина постоянная. Воспользовавшись условием сшивки (41), (42), получаем следующее выражение для скачкообразного изменения вронскиана при пересечении границы a i :

w ( a . ) = -^^ w ( a- ),              (46)

P 0⁽ a - - )

откуда легко получить рекуррентное соотношение w (i) =      w (1)-                      (47)

P 0⁽¹⁾

Окончательно амплитуды первой и второй гармоник запишутся в виде

P 1 ( a ) = юр о, v о G ( a ,0, ю ),

,Л £⁴е ai-

P 2 ( a ) = a ^- i -^J G ( a, 5 ,2 ю )G ²( 5 ,0, ю )d 5 .

- = , p о i l ,

L 2

1 1

^{2 c} 0 P o

= - ² a ₀

ОДНОРОДНАЯ ТРУБА

В качестве примера решим задачу в однослойной среде с плотностью р ₀ = const и скоростью c ₀ = const, - = ю / c ₀, для которой имеем

G ( a , 5 , ю ) =

1     [ cos -a sin - ( L - 5 ),

- cos -L [ cos - 5 sin - ( L - a ),

a ^ 5 ; a > 5 .

Решение задачи (25), (26) с учетом постоянства в слое плотности и скорости звука, таким образом, равно sin -(L - a)

P 1 (a ) = P o ^ю v 0 G ( a ,0, ^ю ) = ^- p 0 c 0 v 0-------—, ⁽⁴⁹⁾

cos -L а решение всей задачи (17), (18) равно

. .            sin - ( L - a )                  ....

P 1 ( a , t ) = - P 0 c 0 v 0------ -—cos ю t .       (50)

cos -L

После нахождения p ₁ можно решать уравнение (19), правая часть которого равна

( / + 1)

sin² - ( L - a ) cos² L

здесь a ₀ равно

^{д 2(} p? ) 2

cos 2 ю t ;

^a 0    ^{2 e} 0 P 0 ^v 0   ²    2    ^P 0 ^v 0 ,

а у = const внутри слоя.

Как видно из (51), вынуждающее воздействие при нахождении p ₂ имеет уже двойную частоту, а резонансные частоты становятся вдвое чаще (фактор cos² -L ):

д2р2    1 д2p2     2 sin2 -(L - a)    ......

--2—^2 = - а ----у—^•cos2 ю t . (53)

д a    c ₀ д t            cos -L

Полагая р 2( a, t) = P2( a )cos2юt,(54)

приходим к задаче d P + (2-)2 p = -2a0 Sin2-(2L - a).(55)

2                2          0

d a                    cos -L

Решение (55) имеет вид

2л_ P 2 ( a ) = -О 0- f G ( a , 5 ,2 ю )sin2 - ( L - 5 )d 5 = cos -L 0
- 2a 0	( a                          2 У 2 < a ) J у 1 ( 5 )sin - ( L - 5 )d 5 + 0	.(56)
w (2 ю )cos2 -L	+ У 1 ( a ) j y 2 ( 5 )sin2 - ( L - 5 )d 5 I           a                                )

В(56)введены обозначения:

w (2 ю ) = - 2 - cos 2 -L , у 1 = cos2 -a ,        (57)

у ₂ = sin 2 - ( L - a ).

Вычисляя (56), получаем

^P 2⁽ a ) = ^-

a ₀

32cos² -L cos 2 -L

X

X

⁴ 3cos2 -a + cos 2 - ( a - 2 L ) -             ²

- 4 cos 2 -L + 2 -a (sin 2 -a + sin 2 - ( a - 2 L ))

. (58)

Окончательно получаем выражение для р ₂( a , t ):

p ₂( a , t ) = P ₂( a )cos2 ю t .              (59)

Таким образом, во втором приближении поле в однослойной трубе определяется выражением

P i⁽ a , t ) = ^- Р о c о ²

d£ i ( a , t ) д a

p ( a , t ) = P i ( a , t ) + p 2 ( a , t ) =

= P 1 ( a )cos to t + P₂( a )cos2 to t ,         (60)

Р 2⁽ a , t )      ^p о c о

д ^ 2 ( a , t ) д a

^{+ Е}Р о С о

р£( a , t) Y V д a ,

где P ₁ ( a ) и P ₂ ( a ) описываются выражениями (49) и (58) соответственно.

Отношение амплитуд примерно равно p2(a, t) p1(a,t)

= V.    2E о     = M     -E о c0cos2kLcoskL     cos2kLcoskL и вне резонанса имеет порядок числа Маха M (что соответствует исходным предположениям о соотношении гармоник). Однако либо в окрестностях резонансов первой гармоники, либо второй амплитуда второй гармоники может существенно вырасти и стать соизмеримой с первой. В этом случае, впрочем, предложенный анализ неправомерен, т. к. для его справедливости необходимо соблюдение условия p1 » p2. Кроме того, из последнего отношения видно, что коэффициент E0 по праву носит название коэффициента нелинейности; при E0 ^ 0 вторая гармоника исчезает.

Отметим, что в работах [5, 6] приведено решение задачи для однородной трубы с точно такими же краевыми условиями, но только в терминах смещений частиц £ в лагранжевой системе координат. После перехода от смещений к давлениям в лагранжевой системе координат по формулам [15, с. 28]

У + 1

где E = 2 , приходим к выражениям (5о) и (58), (59) для первой и второй гармоник давления. Совпадают также выражения для первых двух гармоник колебательной скорости, полученные в [5, 6] дифференцированием соответствующих гармоник смещения по времени, а в настоящей работе — согласно (3), по формулам д v1>2( a, t) =    1  дp1,2( a, t)

д t         p _о     д a

ПРИМЕРЫ

Пример 1. Расчет первых двух гармоник в однородной трубе

Здесь представлены графики амплитуд первой и второй гармоник давления и колебательной скорости. Исходные данные: f = 3 МГц, L = 3 -Ю^-4 м, v _о = 5 - 1о ^{- 2} м/с, Y = 6-1

На рис. 1, 2 представлены амплитуды стоячих волн давлений первой и второй гармоник; на рис. 3, 4 — амплитуды стоячих волн колебательных скоростей первой и второй гармоник.

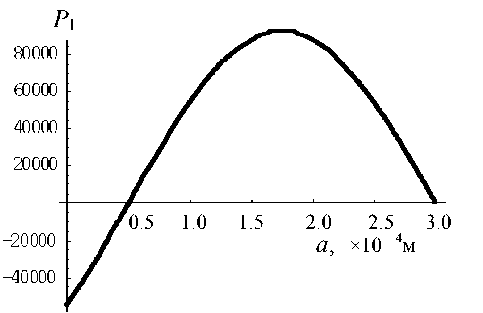
Рис. 1. График зависимости амплитуды 1-й гармоники давления P 1 ( a )

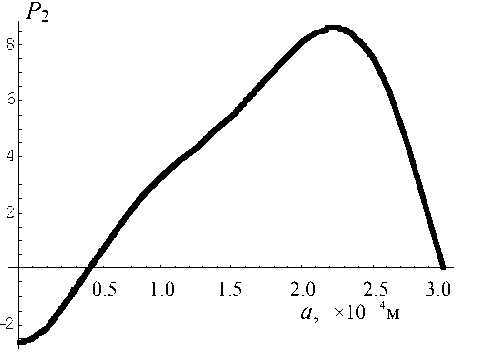
Рис. 2. График зависимости амплитуды 2-й гармоники давления P 2 ( a )

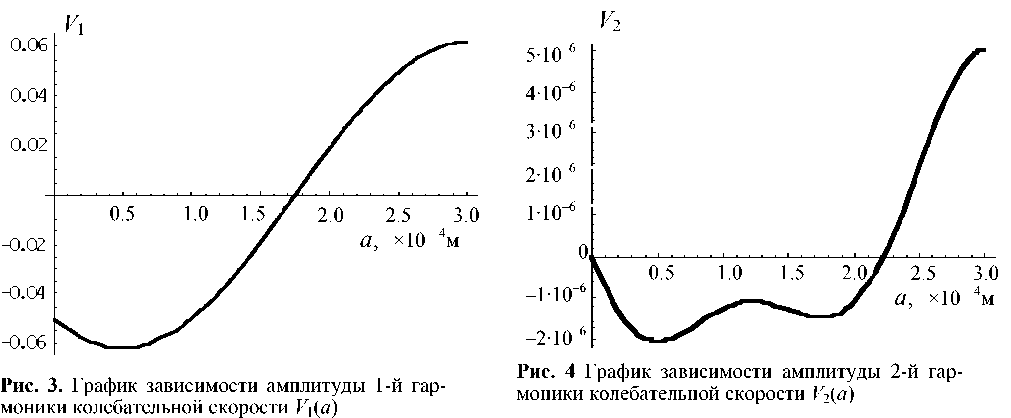
Из графиков видно, что вторые гармоники могут представлять собой стоячие волны неправильной формы.

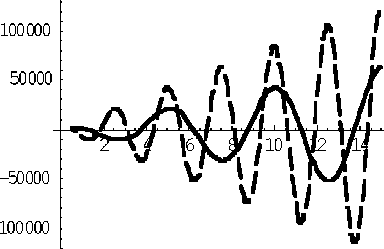
Отдельно остановимся на поведении вронскианов первой и второй гармоник. Из рис. 5 видно, что вронскианы имеют характер линейно нарастающих с частотой гармоник с интервалами меж- ду нулями соответственно

1 с

A f 1 = 1 c ⁰

2 L

и

1 с A f 2 = ¹ c ⁰

4 L

а первые нули находятся соответст- венно в точках f 1 = — и f 2 = —, никогда не 1    4L      1    8L совпадая. При выборе параметров трубы необхо- димо учитывать наличие этих точек резонансов. Реально волновому числу можно приписать мнимую составляющую, зависящую от частоты. В частности, для воды коэффициент затухания при частотах 7-1900 МГц равен а = 25 •Ю-15 • f2 м"1 [10]. Это означает, что волновое число получает положительную добавку ki = ia, которая устраняет бесконечное возрастание амплитуд стоячей волны на резонансах. Например, на частоте f = 10 МГц получаем а = 2.5 м-1. Если принять, что на частотах в окрестности 3 МГц справедлива близкая зависимость коэффициента затухания от частоты, то приблизительно получаем а ~ 0.25 м-1.

Отметим, что предпочтение необходимо отдавать частотам, для которых значение вронскиана находится в окрестностях экстремумов функции зависимости вронскиана от частоты, что обеспечивает более устойчивое поведение амплитуд гармоник при возмущениях частоты или геометрии камеры. Например, при изменении аргумента в окрестностях ± 36 ° (40 % всего диапазона)

w 1, w 2

f , МГц

Рис. 5. Графики зависимости вронскианов 1-й гармоники w 1 (сплошная линия) и 2-й — w 2 (пунктир)

относительно экстремума значение cos меняется всего на 19 %.

Пример 2. Расчет первых двух гармоник в дискретно-слоистой трубе

Рассматривается четырехслойная труба. Характеристики слоев представлены в таблице.

В многослойном волноводе дела обстоят не столь тривиально, как в однослойном, однако особенности формирования поля по-прежнему качественно определяются поведением вронскиана решений первой гармоники. Но в этом случае необходимо детальнее остановиться на физической стороне процесса.

Поскольку при построении первой гармоники давления используется решение y ₂ ( a ), удовлетворяющее только краевому условию при a = L (см. (27), (29)), то при анализе можно рассмотреть

Характеристики слоев в примере 2

№ слоя Скорость звука, м/с Плотность, кг/м3 Толщина слоя, м Y 1 1500 1000 4∙10–2 6.1 2 5570 2600 1∙10–4 6.1 3 1500 1000 3∙10–4 6.1 4 5570 2600 1∙10–4 6.1 сматривать как суммарное поле, образованное падающей из а = -^ плоской волной и волной, отразившейся от границы а = L, т. к. это поле является решением соответствующего дифференциального уравнения и удовлетворяет условию на границе а = L. При этом существенным является наличие бесконечного числа переотражений плоской волны внутри кусочно-неоднородных слоев 2–4. По аналогии с волноводным случаем, когда нормальные волны рассчитываются путем решения дисперсионного уравнения [16, с. 221, 223], рассмотрим поведение произведения

D ( f ) = V 32 (f )V.Af )exp(2 ik з ( f ) d 3 ), (61)

характеризующего степень резонансности слоев 2–4. Здесь V ₃₂ ( f ) — коэффициент отражения пло-

ской волны при ее падении из слоя 3 на слой 2 и далее на полупространство а е ( -~ , d 1 ]; V₃₄ ( f ) — коэффициент отражения плоской волны при ее

падении из слоя 3 на слой 4; k ₃( f ) =

2 п f c ₃

— вол-

новое число в слое 3; d_i — толщина i -го слоя. Соответствующие коэффициенты отражения легко могут быть рассчитаны по методике, изложенной в [16, с. 15–17], и окончательно (61) принимает

вид

z ²— z 3 ₊ z—z i exp(2 ik 2 ( f ) d 2 )

D ( f ) = z ² + z ³    z ¹ + z ²-----------------

1 ₊ z 2 ^z 3 . z ^A exp(2 ik 2 ( f ) d 2 ) z 2 ⁺ z 3 z i ⁺ z 2

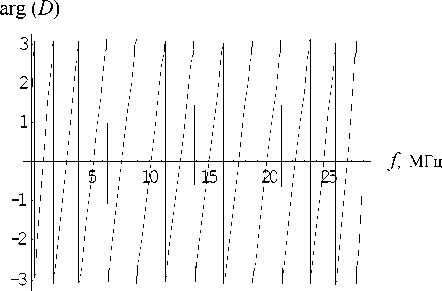
Рис. 7. Зависимость arg( D ( f ))

слоистое полупространство a е ( -” , L ], где первый слой заменен однородным полупространством с идентичными первому слою акустическими характеристиками. Тогда поле y ₂( а ) можно рас-

4^-A - exp(2 ik 4 ( f ) d 4 )

x z ^{4 +} z 3 --exp(2 ik ₃( f ) d ₃). (62)

1 - z 4_Jl exp(2 ik 4 ( f ) d 4 ) z 4 ⁺ z 3

Здесь z i = p i c i — импеданс в i -м слое. На рис. 6, 7 представлены модуль и аргумент функции D ( f ). Модуль функции D ( f ) носит периодический характер; период равен F = 27.85 МГц, что совпадает с первой частотой "полуволновости" слоя 2. На всех частотах, кратных F , модуль функции D ( f ) равен нулю, включая и частоту f = 0. На этих частотах слой 2 прозрачен, и в силу идентичности характеристик слоев 1 и 2 коэффициент отражения V ₃₂( f ) равен нулю. Максимум модуля функции D ( f ) не достигает единицы и равен 0.979, поэтому собственных частот внутри слоев 2–4 не возникает. Поведение аргумента функции D ( f ) представлено на рис. 7; он вследствие его скачкообразного изменения в точках nF , n = 0,1,2,... (см. рис. 9) ведет себя апериодично. Средний интервал

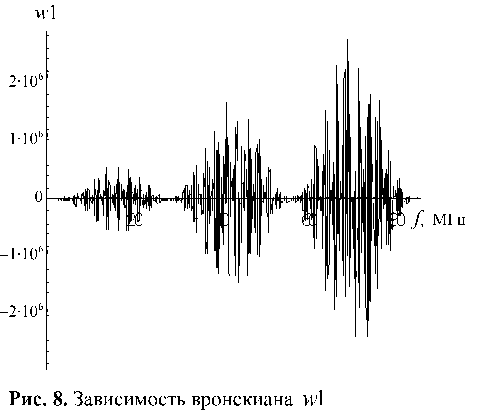
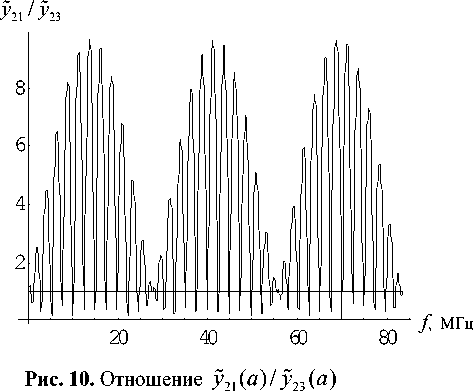
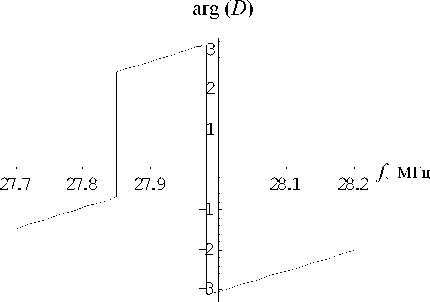
Рис. 9. Зависимость arg( D ( f ))

набега фазы на 2 π составляет примерно 2.4 МГц. На интервале F фаза функции D ( f ) 12 раз оказывается кратной 2 π .

На рис. 8 представлено поведение вронскиана w 1 решений y ₁( a ), y ₂( a ). Сравнивая рис. 6 и 8, заключаем, что период биений в поведении вронскиана в точности совпадает с периодом F . Рассмотрим причину такого совпадения.

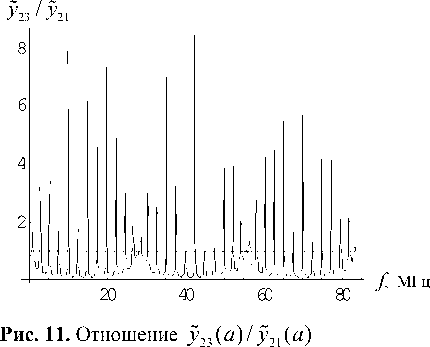
Следует ожидать, что на частотах, при которых фаза функции D(f) кратна 2π , амплитуда функции y2 (a) внутри слоев 2-4 должна резонировать и тем больше, чем больше модуль функции D(f). На рис. 10 представлена зависимость отношения амплитуды y2(a) внутри слоя 1 (y21(a)) к амплитуде y2(a) внутри слоя 3 (y23(a)). На рис. 11 представлено обратное отношение. Как видно, периодичность вновь составляет F. Горизонтальная прямая на рис. 10, 11 проходит на уровне 1. Таким образом, амплитуда внутри слоя 3 за счет резонансных явлений может практически на порядок превышать амплитуду внутри слоя 1. На рис. 12, 13 представлены те же зависимости в более крупном масштабе, а именно на интервале, где фаза функции D(f) меняется дважды от -π до π . На рис. 14 представлено поведение вронскиана в этом же диапазоне. Видно, что поведение огибающей вронскиана совпадает с поведением кривой на рис. 12 с поправкой на то, что амплитуда вронскиана пропорциональна волновому числу.

Наконец, на рис. 15 представлено поведение вронскиана в окрестностях f = 2.94534 МГц, где фаза функции D ( f ) равна нулю и тем самым где резонирует амплитуда в слое 3.

Как видно, поведение вронскиана имеет характер промодулированной низкой и высокой частотой

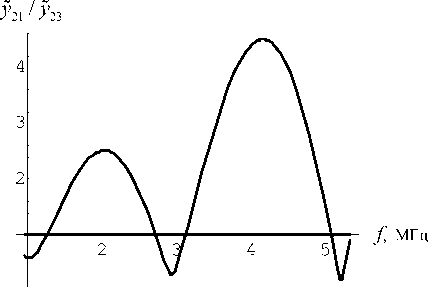
Рис. 12. Фрагмент графика (рис. 10) y₂₁(a)/ y ₂₃( a )

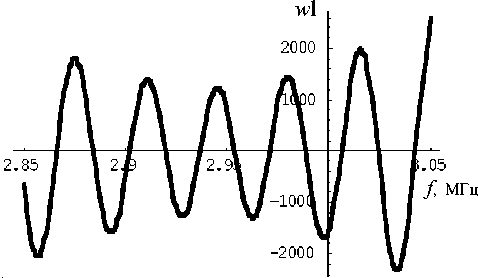
Рис. 15. Фрагмент графика (рис. 14) вронскиана w 1

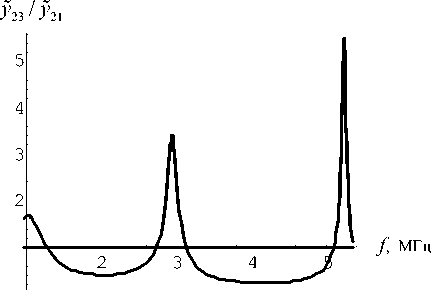
Рис. 13. Фрагмент графика (рис. 11) y ₂₃ ( a ) / y ₂₁ ( a )

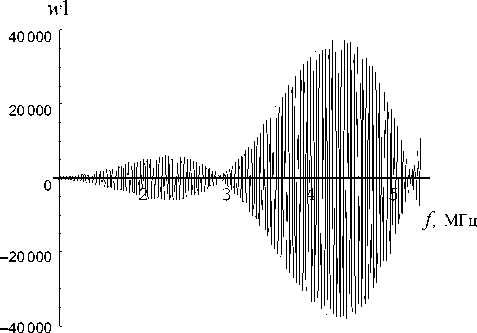
Рис. 14. Зависимость вронскиана w 1

гармоники с линейным трендом, пропорциональным частоте. Низкая частота связана с периодичностью изменения модуля, а высокая — с периодичностью изменения фазы функции D ( f ). Таковы же зависимости отношений амплитуд первой гармоники, пропорциональных решению y ₂( a ), в первом и третьем слоях.

Для выбора рабочей частоты озвучивания трубы необходимо руководствоваться необходимым числом узлов, например, амплитуды давления первой гармоники в нужном слое (например, в слое 3), а также тем, должен ли рабочий слой резонировать или, наоборот, антирезонировать. Кроме того, остаются справедливыми рекомендации по выбору частоты с точки зрения поведения вронскиана, описанные выше.

Число узлов m в l -м слое толщиной L_l легко может быть рассчитано по следующей простой формуле:

m = в ( n ) = n v ( n + 1) (63)

при условии n < ^l < n +1. (64)

A _l /2 ’

Здесь A _l — длина волны в l -м слое; значок v означает логическое ИЛИ. Принимая L_l = = 3 х 10 ^{- 4} м, получаем, что m = в (1) = 1 v 2 при условии f е [2.5,5) МГц.

Ниже рассчитаны параметры акустического поля для первых двух гармоник для частот 3.00000, 2.94534 и 4.39783 МГц, подобранных из следующих соображений. Число узлов не более 2, значение вронскиана близко к максимуму, и частоты находятся либо в окрестностях резонанса (3.00000 МГц), либо антирезонанса в слоях 2–4 (2.94534 и 4.39783 МГц).

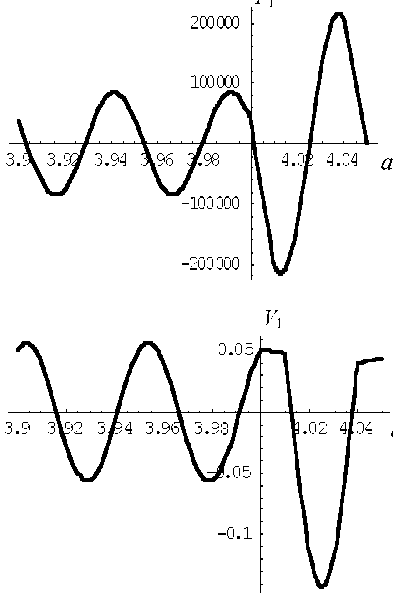
Рис. 16. Амплитуды давления и колебательной скорости первых двух гармоник; f = 3 х 10⁶ Гц

в

P 2

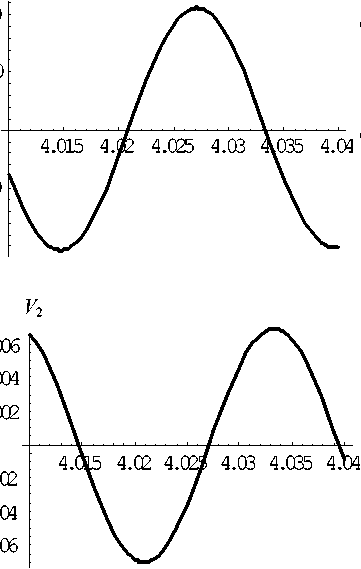
б a, xio2м

г a, xio2м

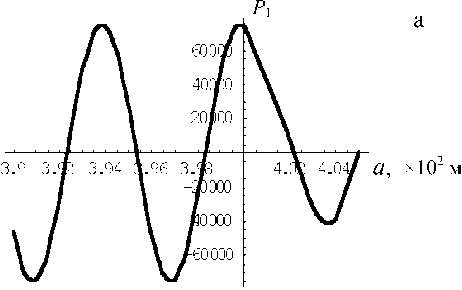
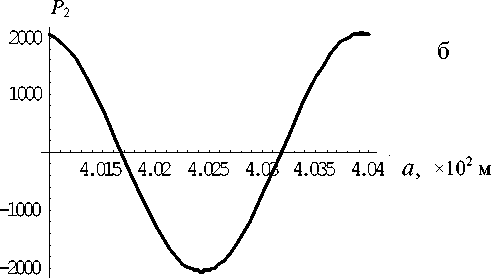
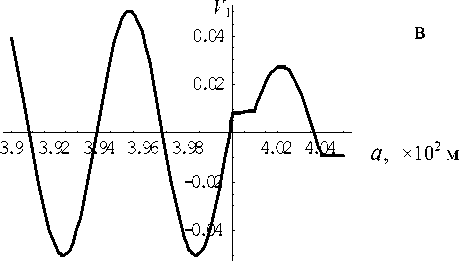
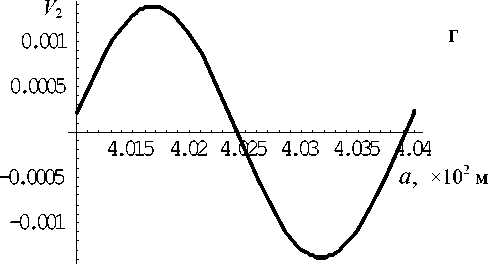
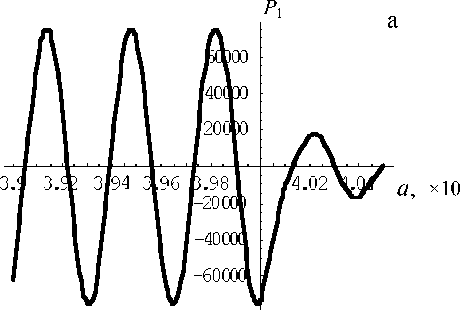
Рис. 17. Амплитуды давления и колебательной скорости первых двух гармоник; f = 2.5041 х 10⁶ Гц

V 2

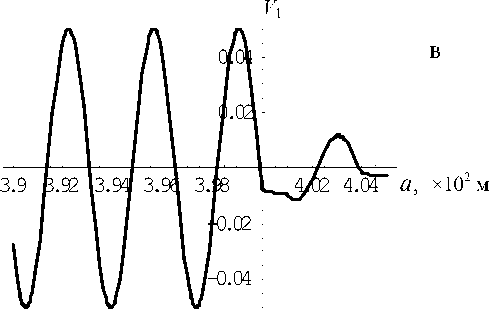
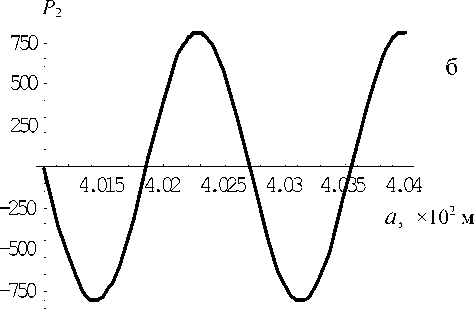
Рис. 18. Амплитуды давления и колебательной скорости первых двух гармоник; f = 4.39783 х 10 6 Гц

0.0004

0.0002

-0.0002

-0.0004

y 2

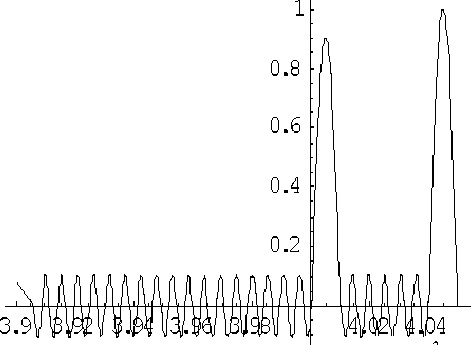
a , ×10² м

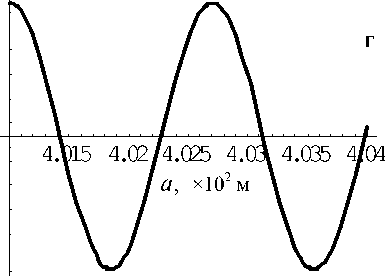
Рис. 19. Поведение функции y ₂( a ) на частоте просветления f = 27.85 МГц

На рис. 16–18 представлены результаты расчетов амплитуд давления и колебательной скорости в стоячей волне первых двух гармоник в много- слойной трубе при частотах вынуждающих колебаний f = 3 МГц (рис. 16), f = 2.5041 МГц (рис. 17) и f = 4.39783 МГц (рис. 18). Амплитуда скорости поршня v0 = 0.5м/с. Поле первой гармоники (давление (а) и скорость (в)) рассчитывалось во всех слоях, а поле второй гармоники (давление (б) и скорость(г)) рассчитывалось только в третьем слое (рабочей зоне). Различие в амплитудах составляет более 2 порядков во всех примерах. Во всех случаях первые гармоники имеют 1 или 2 узла; вторые гармоники имеют до 4 узлов.

Кроме того, как видно из сравнения рис. 16–18, в случае наличия резонансных явлений в рамках слоя, состоящего из 2-го–4-го слоев, амплитуды давления и скорости в нем резко возрастают по сравнению с амплитудами в первом слое (рис. 16). И наоборот, в отсутствие резонанса внутри совокупного слоя 2—4 амплитуды в нем много меньше, чем в слое 1.

В заключение приведем поведение функции y ₂( a ) в случае просветления слоя 2, т. е. на частоте f = 27.85 МГц (см. рис. 19).

Как видно, амплитуды в слоях 1 и 2 совпадают, а в слоях 2 и 4 резко возрастают, что необходимо учитывать при проектировании рабочих ультразвуковых камер.

ВЫВОДЫ

В статье получены общие выражения для поля конечной амплитуды в трубе с переменной плотностью и скоростью для первых двух гармоник давления и скорости, и в частности в однослойной и многослойной трубах. По полученным выражениям произведены расчеты. Выявлены некоторые явления, происходящие в озвучиваемой многослойной трубе. Результаты могут быть полезны в теории и практике использования ультразвука конечной амплитуды.

Работа выполнена при поддержке фонда РФФИ, грант № 05-03-33108.