О вынужденных колебаниях трех тел, упруго опертых на балку
Автор: Баргуев С.Г., Нестеров А.С., Васильев А.А.
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Математическое моделирование и обработка данных
Статья в выпуске: 3, 2024 года.
Бесплатный доступ
В данной статье ставится задача о вынужденных колебаниях трех тел, упруго опертых на балку. Для решения поставленной задачи, в отличие от классического способа, когда система разбивается на части, для которых составляются уравнения движения, находятся их решения, а затем производится сшивка решений в местах разбивки, в данной статье применяется вариационный принцип Гамильтона, в результате чего получается система дифференциальных уравнений, три из которых представляют собой обыкновенные дифференциальные уравнения второго порядка относительно времени, описывающих движение твердых тел, и дифференциальное уравнение в частных производных второго порядка относительно времени и четвертого порядка относительно продольной координаты точек балки. Решение полученной системы ищется в виде произведения амплитуд на гармоническую функцию частоты внешнего возмущающего возмущения. При этом для твердых тел амплитуды постоянные величины, а для балки - переменные. Затем после некоторых преобразований полученной системы амплитудных уравнений, определяются коэффициенты передач в виде отношений указанных амплитуд к амплитуде возмущений. Сказанное относится к методике исследования на вынужденные колебания трех, упруго закрепленных вдоль балки твердых тел, в основе которой лежит вариационный принцип Гамильтона. При этом решение полученной в результате применения вариационного принципа гибридной системы дифференциальных уравнений, включающей как обычные дифференциальные уравнения, так и в частных производных, понимается в обобщенном смысле. Применение понятия обобщенного решения вызвано присутствием в уравнениях дельта-функции Дирака, которую необходимо учитывать в местах присоединения тел к балке. По найденным коэффициентам передачи выявляются резонансные частоты, и производится их сравнение с собственными частотами указанной механической системы.
Балка, упруго закрепленные тела, резонансные частоты, собственные частоты, коэффициенты передач
Короткий адрес: https://sciup.org/148329912
IDR: 148329912 | УДК: 51-7 | DOI: 10.18101/2304-5728-2024-3-45-55
On the forced vibrations of three bodies elastically supported on a beam
In this article, the problem of forced vibrations of three bodies elastically supported on a beam is posed. To solve this problem, in contrast to the classical method, when the system is divided into parts for which equations of motion are compiled, their solutions are found, and then solutions are stitched together in the breakdown methods, Hamilton's variational principle is applied in this article, resulting in a system of differential equations, three of which are ordinary second-order differential equations with respect to time describing the motion of solids, and the partial differential equation of the second order with respect to time and the fourth order with respect to the longitudinal coordinate of the beam. The solution of the resulting system is sought in the form of the product of the amplitudes on the harmonic function of the frequency of the external disturbing disturbance. At the same time, for solids, the amplitudes are constant values, and for a beam, they are variable. Then, after some transformations of the resulting system of amplitude equations, the transmission coefficients are determined in the form of ratios of these amplitudes to the amplitude of disturbances. The above refers to the method of investigating the forced vibrations of three solids elastically fixed along the beam, which is based on the Hamilton variational principle. At the same time, the solution of the hybrid system of differential equations obtained as a result of the application of the variational principle, which includes both ordinary differential equations and partial derivatives, is understood in a generalized sense. The application of the concept of a generalized solution is caused by the presence in the equations of the Dirac delta function, which must be taken into account at the places where bodies are connected to the beam. According to the found transmission coefficients, resonant frequencies are determined, and they are compared with their own frequencies of the specified mechanical system.
Текст научной статьи О вынужденных колебаниях трех тел, упруго опертых на балку
Упругие балки или стержни являются элементами многих конструкций и устройств в авиационной и космической технике, на зданиях и сооружениях, наземном и водном транспорте, опорах линий электропередач, башнях, мачтах, антеннах, трубопроводах и т.п. При вынужденных колебаниях в таких конструкциях возможен резонанс, то есть когда частота приложенных к ним внешних возмущений совпадает с частотой собственных колебаний конструкций. Поэтому возникает необходимость отстройки от резонанса, заключающемся в установке дополнительных гасителей колебаний в виде твердых тел или масс с упругими связями. В задачу исследования вынужденных колебаний входит определение коэффициентов передач, представляющих отношение амплитуд объектов конструкции к амплитуде внешних возмущений в зависимости от их частоты. Построение таких зависимостей позволяет определять резонансные, или то же самое собственные частоты. К теме вынужденных колебаний следует отнести начально-краевую задачу, то есть исследование поведения механической системы во времени при заданных начальных условиях. Гибридная система дифференциальных уравнений, описывающая движение рассматриваемой механической системы, выведена с использованием вариационного принципа Гамильтона [1], при этом точечное взаимодействие балки с прикрепленной системой твердых тел учитывается дельтафункцией Дирака, что предусматривает применение понятия обобщенного решения обыкновенного дифференциального уравнения четвертого порядка решении при описании амплитудных смещений точек оси балки.
В данной работе описывается методика исследования механической системы на вынужденные колебания с получением коэффициентов передач. Производится идентификация резонансных частот с собственными
1 Исследование вынужденных колебаний
Рассмотрим механическую систему (рис. 1), состоящую из трех тел с массами m 1 , m 2, m 3, присоединенных к упругому стержню с помощью пружин жесткости c 1 , c 2 и c 3 соответственно. Концы стержня жестко закреплены. Массы m 1 , m 2, m 3 могут перемещаться только поступательно в направлении осей O 1 z 1 , O 2 z 2, O3z 3 соответственно . Здесь точки O 1 , O2, O3 совпадают с положениями равновесия масс и являются фиксированными. Колебания масс характеризуются функциями z 1 (t ), z 2( t ), z 3( t ). Перемещения точек стержня описываются функцией u ( x , t ). Пружины присоединены к стержню на расстояниях а 1 , a 2, а 3 от левого конца стержня соответственно. На массы m 1 , m 2, m 3 действуют гармонические силовые возмущения с частотой p и амплитудами F , F 2, F3 .
Тогда вариационный принцип Гамильтона может быть выражен следующим соотношением:
j ( 8 (Т - U ) + 8 W ) dt = 0,
где T — кинетическая энергия системы; U — потенциальная энергия системы; 5W — виртуальная работа неконсервативных сил.
Потенциальная и кинетическая энергия системы складываются соответственно из энергии тел, стержня и пружин, т.е.
T = T + Т2 + Т3 + Тб, U = U1 + U2 + U3 + Uб, где
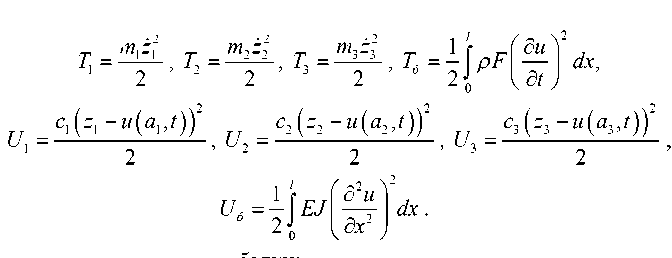
Т = mz 2
m 2 z 2
_ m 3 z 3 2
, 3 2 , б c2 (z2 - u (a2, t))
1 2 ’ c (z1 - u (a1, t
, U 3
l
3 j EJ
2 о dx dx2
Здесь p — плотность балки; F — площадь поперечного сечения стержня; EJ — жесткость балки на изгиб; Т — кинетическая энергия i -ой массы; Т б — кинетическая энергия балки; U i — потенциальная энергия
упругой деформации i -ой пружины; U б — потенциальная энергия упругой деформации балки.
Внешние гармонические силовые возмущения определяются по формулам:
F (t) = F cos pt, F2 (t) = F2 cos pt, F3 (t) = F3 cos pt, следовательно:
S W = F cos pt S z1 + F2 cos pt S z 2 + F3 cos pt S z 3
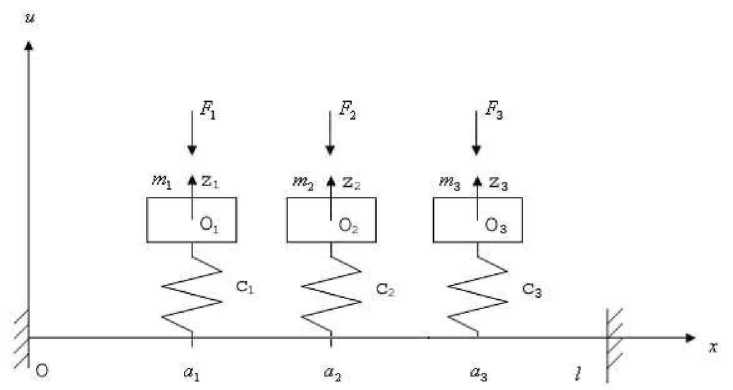
Рис. 1. Балка с тремя упруго закрепленными на ней телами, с действующими на них внешними гармоническими возмущениями.
После ряда преобразований (1) примет вид:
t 1
j[(-m1z‘-c1(z1 - u (a1, t)) + Fcos pt )Sz1 + (-m2 z2 -c2( z2 - u (a2, t)) + F2cos pt )Sz 2 + t0
L
+ ( - m 3 z” 3 - c 3 ( z 3 - u ( a 3 , t )) + F3 cos pt ) S z 3 + j ( c 1 ( z 1 - u ( x , t)) S (x - a1) + (2)
d 2 u d 4 u
+ c 2 ( z 2 - u ( x , t )) S ( x - a 2) + c 3 ( z 3 - u ( x , t )) S ( x - a ,) - p F —2 - EJ — S ^ddx ] dt = 0
2 2 2 3 3 3 d t 2 d x4
Таким образом, получим уравнение движения системы m, z, + c1(z1 - u (a,, t)) = F, cos pt m2 z2 + c2(z2 - u (a2, t)) = F2cos pt m3 z3 + c3(z3 - u (a3, t)) = F3 cos pt
P F F u + EI T uu = L c ( z - u ( x , t )> ^ ( x - a i ) d t d x = i
Поделив первое уравнение на m , , второе на m 2 , а третье на вертое на p F, получим:
z"( t) + p,2 (z1 - u (a,, t)) = Hj cos pt, z2'(t) + p2(z2 - u (a2, t)) = H2 cos pt, z3'(t) + p32(z3 - u (a3, t)) = H3cos pt d2и ,54u Л , z
+ b = L e ( z i - u ( x , t)) S ( x - a )),
U t dx cF. c где p= ,e = —,Hi = F-,ei= ,i = 1,2,3
у m i p F m i
На u(x, t) наложены граничные условия: u (0, t) = u (l, t) = 0, dudu
—(0, t) = —(l, t) = 0 dxdx
m 3 , чет-
.
Подставив в (4) zi (t), u(x, t) в виде zi (t) = Д cos pt, u (x, t) = V(x) cos pt, i = 1,2,3
после преобразования получим:
- p2A + p , 2(4 - V ( a , )) = H i ,
-
- p 2 A 2 + p 22 ( A 2 - V ( a 2 )) = H 2 ,
-
- p 2 A 3 + p 32 ( A 3 - V ( a 3 )) = H 3 ,
-
- p2V(x) + bdVx = Lei(Ai - V(x))S(x - ai).
-
dx
Последнее уравнение в (6) имеет решение
V(x) = V (x - a,)e, (A, - V(a,)) + V2 (x - a2)e2 (A2 - V (a2))+
+V3 (x - a3)e3 (A3 - V (a3))
где V ( x - at ) , i = ,,2,3 — решения основной краевой задачи [,].
Подставляя в (7) последовательно x = a1, x = a2, x = a3 получаем систему линейных алгебраических уравнений относительно
V ( a 1 ), V ( a 2 ), V ( a 3 )
( 1 + V i ( 0 ) e1 ) V ( a1 ) + V 2 ( a1
= £ Via, — a.\e.A., i 1i ii i = 1
—
a 2 ) e 2 V ( a 2 ) + V 3 ( a l a 3 ) e 3 V ( a 3 )
V ( a 2 — a 1 ) eV ( a 1 ) + ( 1 + V 2 ( 0 ) e 2 ) V ( a 2 ) + V 3 ( a 1 — a 3 ) e3V ( a3 ) =
^i\ a 2 ai ) eiAi ,
-
a 2 ) e2V ( a 2 )+ ( 1 + V 3 ( 0 ) e 3 ) V ( a 3 )
V1(a 2 al) e1V(al) + V2(a3 = i=1V'( a3 - ai) eA'
Решая систему (8), получаем
V (a, ) = в A + ei2 a 2 + в A3,
V ( a 2 ) = в 21 A + £ 22 A + в 23 A 3 , (9)
V ( a 3 ) = в 31 A 1 + в 32 A + в 33 A 3 .
где
£ 12 = 1
A в13 =1 A в4
|
_ V ( 0 ) e V ( a 2 — a 1 ) e 1 V ( a 3 — a 1 ) e 1 |
V 2 ( a 1 — a 2 ) e 2 1 + V2 ( 0 ) e 2 V 2 ( a 3 — a 2 ) e 2 |
V 3 ( a 1 — a 3 ) e 3 V 3 ( a 2 — a 3 ) e 3 1 + V3 ( 0 ) e 3 |
|
V 2 ( a 1 — a 2 ) e 2 |
V 2 ( a 1 — a 2 ) e 2 |
V 3 ( a 1 — a 3 ) e 3 |
|
_ V 2 ( 0 ) e 2 |
1 + V2 ( 0 ) e 2 |
V 3 ( a 2 — a 3 ) e 3 |
|
V 2 ( a 3 — a 2 ) e 2 |
V 2 ( a 3 — a 2 ) e 2 |
1 + V3 ( 0 ) e 3 |
|
V 3 ( a 1 — a 3 ) e 3 |
V 2 ( a 1 — a 2 ) e 2 |
V 3 ( a 1 — a 3 ) e 3 |
|
V 3 ( a 2 — a 3 ) e 3 |
1 + V2 ( 0 ) e 2 |
V 3 ( a 2 — a 3 ) e 3 |
|
V 3 ( 0 ) e 3 |
V 2 ( a 3 — a 2 ) e 2 |
1 + V3 ( 0 ) e 3 |
,
,
,
|
0 21 = |
1 A |
_1 + V ( 0 ) e 1 V ( a 2 - a 1 ) e 1 V ( a 3 - a 1 ) e 1 |
_ V ( 0 ) e V ( a 2 - a 1 ) e V ( a 3 - a 1 ) e 1 |
V 3 ( a 1 - a 3 ) e 3 V 3 ( a 2 - a 3 ) e 3 1 + V 3 ( 0 ) e 3 |
|
|
0 22 =- |
1 A |
_1+ V ( o ) e V ( a 2 - a 1 ) e 1 V ( a 3 - a 1 ) e 1 |
V2 ( a 1 - a 2 ) e 2 _ V 2 ( 0 ) e 2 V 2 ( a 3 - a 2 ) e 2 |
V 3 ( a 1 - a 3 ) V 3 ( a 2 - a 3 ) 1 + V3 ( 0 ) e |
e 3 e 3 |
|
0 23 = |
1 A |
_1 + V ( 0 ) e 1 V ( a 2 - a 1 ) e V ( a 3 - a 1 ) e 1 |
V 3 ( a 1 - a 3 ) e 3 V 3 ( a 2 - a 3 ) e 3 V 3 ( 0 ) e 3 |
V 3 ( a 1 - a 3 ) e 3 V 3 ( a 2 - a 3 ) e 3 1 + V 3 ( 0 ) e 3 |
|
|
0 31 = |
1 A |
_1 + V ( 0 ) e 1 V ( a 2 - a 1 ) e V ( a 3 - a 1 ) e 1 |
V 2 ( a 1 - a 2 ) e 2 1 + V 2 ( 0 ) e 2 V 2 ( a 3 - a 2 ) e 2 |
_ V ( 0 ) e V ( a 2 - a 1 ) e V ( a 3 - a 1 ) e 1 |
|
|
0 32 = 1 A |
_1+ V ( 0 ) e V ( a 2 - a 1 ) e 1 V ( a 3 - a 1 ) e 1 |
V 2 ( a 1 - a 2 ) e 2 1 + V2 ( 0 ) e 2 V 2 ( a 3 - a 2 ) e 2 |
V 2 ( a 1 - a 2 ) e 2 _ V 2 ( 0 ) e 2 V 2 ( a 3 - a 2 ) e 2 |
||
|
0 33 =- |
1 A |
_1+ V ( 0 ) e V ( a 2 - a 1 ) e V ( a 3 - a 1 ) e 1 |
V 2 ( a 1 - a 2 ) e 2 1 + V2 ( 0 ) e 2 V 2 ( a 3 - a 2 ) e 2 |
V 3 ( a 1 - a 3 ) e 3 V 3 ( a 2 - a 3 ) e 3 V ( 0 ) e 3 |
|
|
A = |
_1 + V ( 0 ) e 1 V ( a 2 - a 1 ) e 1 V 1 ( a 3 - a 1 ) e 1 |
V 2 ( a 1 - a 2 ) e 2 1 + V2 ( 0 ) e 2 V 2 ( a 3 - a 2 ) e 2 |
V 3 ( a 1 - a 3 ) e 3 V 3 ( a 2 - a 3 ) e 3 1 + V 3 ( 0 ) e 3 |
. |
|
Подставляя (9) в первые три уравнения системы (6), получаем следующую систему:
( P 2 - p 2 - P 2 0 11) A 1 - P 2 0 12 A 2 - P 2 0 13 A 3 = H 1 ,
-
- p 2 0 21 A 1 + ( p 2 - p - p 2 0 22) A 2 - p 2 в 23 A 3 = H 2 , (10)
p 3 0 31 A 1 - p 3 0 32 A 2 + ( p 3 - p - p 3 0 3з) A 3 = H 3 .
Отсюда , решая систему , найдем
Л A] i A2 Л A3
A 1 А , A 2 А , A 3 А .
AAA где
∆=
H 1
∆ 1 = H 2
∆2 =
∆3 =
p 1 2
H 3
p 1 2
p 1 2
- p 1 2 β 12 - p 1 2 β 13
p 2 - p - p 2 β 22 - p 2 β 23
- p 3 β 32 p 3 - p - p 3 β 33
- p 2 - p 1 2 β 11
- p 2 2 β 21
- p 3 2 β 31
- p 2 - p 1 2 β 11
- p 2 2 β 21
- p 3 2 β 31
- p 2 - p 1 2 β 11
- p 2 2 β 21
- p 3 2 β 31
H 1 - p 1 2 β 13
H 2 - p 2 2 β 23
H 3 p 3 2 - p 2 - p 3 2 β 33
- p12β12
p2 -p-p2 β22
- p32β32
- p 1 β 12 - p 1 β 13
p 2 - p - p 2 β 22 - p 2 β 23
- p 3 β 32 p 3 - p - p 3 β 33
Поделив A1,A2,A3 соответственно на F1,F2,F3 получим коэффициенты передачи
∆∆∆ χ 1( p ) = 1 , χ 2 ( p ) = 2 , χ 3 ( p ) = 3
.
∆ F 1 ∆ F 2 ∆ F 3
-
2 Расчеты коэффициентов передач
В работе рассчитаны коэффициенты передач с помощью Web-программы, разработанной авторами. При этом использованы параметры рассматриваемой механической системы, взятой из зарубежной статьи [2].
Параметры балки с упруго закрепленными тремя телами в системе СИ: k 1 = 3 kb , m 1 = 0,2 mb , k 2 = 4,5 kb , m 2 = 0,5 mb , k 3 = 6 kb , m 3 = 1 mb , kb = 63476,1, mb = 15,3875, a 1 = 0,1, a 2 = 0,4, a 3 = 0,8, l = 1, EJ = 63476,1, ρ F = 15,3875.
Результаты работы программы.
Ниже показаны графики зависимости коэффициентов передач от частоты внешних гармонических возмущений при равных амплитудах F1=F2=F3=F.
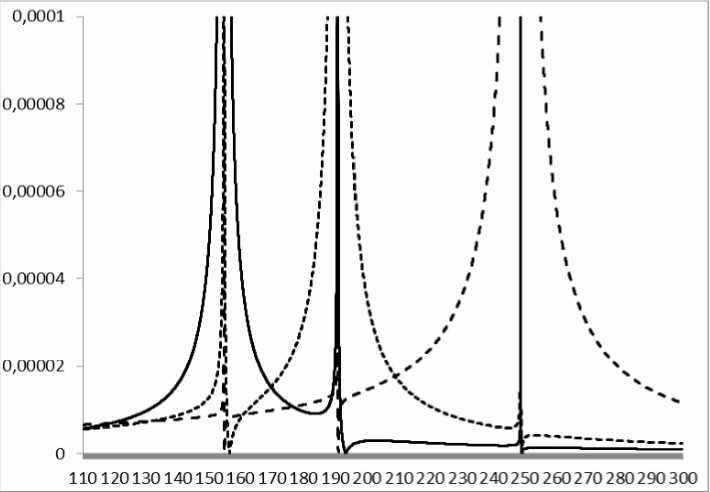
Собственные частоты, полученные в зарубежной статье
|
ω 1 |
ω 2 |
ω 3 |
ω 4 |
ω 5 |
|
|
Зарубежная статья [2] |
156,6703 |
190,6994 |
248,6622 |
1454,2932 |
3968,4732 |
Графики показывают, что несколько первых резонансных частот по порядку величины совпадают с собственными частотами, приведенные в таблице.
Заключение
В результате исследования вынужденных колебаний рассматриваемой механической системы выведены соотношения для коэффициентов передач в зависимости от частоты внешних гармонических возмущений. Определены резонансные частоты, которые совпали по порядку величины с собственными, что говорит об эффективности предложенной методики. Отметим, что определение резонансных частот производится с меньшими усилиями, чем определение собственных частот, которое требует применения громоздкого аппарата.
Список литературы О вынужденных колебаниях трех тел, упруго опертых на балку
- Мижидон А. Д., Баргуев С. Г. Краевая задача для одной гибридной системы дифференциальных уравнений // Вестник Бурятского государственного университета. Математика, информатика. 2013. № 9. С. 130-137. EDN: QZFPMB
- Wu J.S., Chou H. M. A new approach for determining the natural frequencies and mode shapes of a uniform beam carrying any number of sprung masses. Journal of Sound and Vibration. 1999; 220 (3): 451-468.
