О взаимосвязи двух классов решений уравнений Навье - Стокса. II
Автор: Левенштам Валерий Борисович
Журнал: Владикавказский математический журнал @vmj-ru
Статья в выпуске: 4 т.14, 2012 года.
Бесплатный доступ
Статья дополняет работу автора [1], посвященную вопросам разрешимости начально-краевой задачи для уравнений Навье - Стокса с полиномиально зависящей от неизвестной (скорости) массовой силой. Здесь установлена локальная разрешимость указанной задачи в обобщенном смысле и изложено доказательство одной важной леммы из [1].
Уравнения навье - стокса, локальная разрешимость, проектор вейля
Короткий адрес: https://sciup.org/14318401
IDR: 14318401 | УДК: 517.633
Текст научной статьи О взаимосвязи двух классов решений уравнений Навье - Стокса. II
Данная статья является продолжением статьи [1], но ее можно читать, по существу, независимо. Напомним, что в [1] рассматривается начально-краевая задача для уравнений Навье — Стокса с полиномиально зависящей от неизвестной (скорости) массовой силой. Там введены определения решения и обобщенного решения указанной задачи и получены условия, при которых обобщенное решение, если оно существует, является обычным решением. В настоящей, заключительной, части работы: 1) показано, что обобщенное решение данной задачи существует, по крайней мере, локально; 2) проведено доказательство важной леммы 1 статьи [1], которая впервые была сформулирована в работе И. Б. Симоненко [2], где лишь намечен путь ее доказательства. В [1] имеются ссылки (вместо доказательства леммы 1) на монографию И. Б. Симоненко [3] и заметку автора [4], а также замечание о том, что в монографии [3] доказательство для нашего случая (граница области ∂Ω ∈ C 2 ) — неполное (оно полное для ∂Ω ∈ C 5 , но переход к ∂Ω ∈ C 2 представлен лишь схематично). Ввиду труднодоступности сборника [4] мы воспроизводим здесь содержащееся в нем полное доказательство леммы сразу для ∂Ω ∈ C 2 . Отметим еще, что 3) некоторые важные детали [1], которые используются и в данной статье, представлены здесь подробнее. Это также является целью данной заметки.
Результаты [1] и данной статьи потребовались автору для обоснования метода усреднения для уравнений Навье — Стокса с полиномиально зависящей от скорости массовой силой, содержащей высокочастотные слагаемые с большими амплитудами. Работа по обоснованию направлена в печать. Она, в свою очередь, примыкает к исследованиям автора (см., например, [5–10]) асимптотических свойств некоторых важных классов эволюционных уравнений в частных производных с большими высокочастотными слагаемыми.
1 ° . Пусть Q — ограниченная область евклидова пространства R 3 с C 2 -гладкой границей dQ , m — целое неотрицательное, n — натуральное, а v и T — положительные числа. В цилиндре Q = Q х [0, T] рассмотрим начально-краевую задачу вида
∂v∂
—--vAv + VP + (v, V)v = 2 —ai (v,x,t) + b(v,x,t), div v = 0,
∂t∂x
16j63
v|SQx(G,T ] = 0,
v(x, 0) = vo(x), x E Q, в которой неизвестными являются вектор-функция v(x,t) и функция P(x,t) со значениями в R3 и R1 соответственно2, ш — большой параметр.
Будем предполагать, что вектор-функции a j ( v,x,t ) и b(v,x,t) со значениями в R 3 имеют следующую структуру:
a j = £ a jk , b = £ b k ,
G6k6m G6k6m где ajk(v,x,t) и bk(v,x,t) являются однородными формами степени к относительно компонент вектора v. Таким образом, компоненты ajk' и bk' вектор-функций ajk и bk имеют вид:
a jk' ( v,x,t ) = £ a j' (x,t)v i 1 v s 2 v s 3 ,
|S|=k bk'(v,x,t) = X b' (x,f)vsvs2v33•
| i | = k
Здесь s = (s i , s 2 ,s 3 ) , S j = 0,1,...,k , | s | = s 1 + s 2 + S 3 , v j (j = 1, 2, 3 ) — компоненты вектора v . Прежде чем ввести остальные ограничения на данные задачи (1)–(3), напомним определение известного банахова пространства, которое будет часто использоваться в дальнейшем.
Пусть — го < a < b < +ro и B — банахово пространство. Через C([a, b], B) обозначим банахово пространство непрерывных вектор-функций u : [a, b] ^ B с нормой llullcWbB) = max ku(t)kB.
ii
Будем рассматривать данные a j' ( . , t) и b ' ( . , t) как вектор-функции от t со зна- ii чениями в соответствующих банаховых пространствах и предполагать, что aj' ,b' E C([0, T], L^(Q)), vg E Sq0, qo > max(3(m— 1), 3). Здесь Sq0 = Sq0(Q) — известное в математической гидродинамике вещественное пространство соленоидальных векторов (см. [11, 12] и п. 2° ниже).
2 ° . Задачу (1)-(3) можно интерпретировать как математическое обобщение известной [11, 12] модели движения вязкой несжимаемой жидкости ( v — скорость жидкости, P — давление в ней) в сосуде под действием массовой силы. Обобщенная массовая сила здесь представлена правой частью первого уравнения (1). Она помимо пространственных и временной переменных x , t зависит и от скорости v движения жидкости. Систему вида (1) мы, следуя работе [2], называем уравнениями Навье — Стокса.
Приведем некоторые результаты математической гидродинамики [11, 12], на которые будем опираться в дальнейшем.
Пусть M — множество непрерывно дифференцируемых в Q соленоидальных (т. е. удовлетворяющих уравнению div v = 0 в Q ) вектор-функций v(x) с равной нулю на dQ нормальной компонентой. Через S q , q > 1 , обозначим банахово пространство, являющееся замыканием множества M по норме L q = L q (Q) :
) 1 /q = (/[X v(x) l 2l q/2 dx) 1 /q .
Ilvlk = ( J | v(x) | q dx
Ω
Ω 1 6 j 6 3
Ω
Через G q обозначим банахово пространство, полученное замыканием множества градиентов гладких функций ϕ по норме
1/q liwik =
|∇ϕ|q dx k∇ϕkLq.
Ω
Пространство L q распадается в прямую сумму своих подпространств S q и G q : L q = S q ® G q . Связанный с этим разложением проектор П : L q ^ S q является ограниченным оператором, причем ортогональным в случае q = 2 .
В пространстве S q определен оператор A o = — vПА с областью определения D(A o ) =S 2 , являющейся замыканием по норме W 2 множества M . Оператор A o замкнут, а — A o порождает в S q аналитическую полугруппу e -tA 0 , t > 0 . Более того, оператор A 0 сильно позитивен (определение см. в [13, с. 298]), а потому определены его
Y ◦ 2Y дробные степени A0, y > 0 [13, формула (14.15)]. Через S q будем обозначать банахово пространство, элементы которого принадлежат области определения оператора A0γ и снабжены нормой ||ukо2 = ||Aquksq-
S q
3 ° . Введем определения решения и обобщенного решения начально-краевой задачи (1)–(3).
Решением задачи (1)–(3) назовем определенную в цилиндре Q трехмерную вещественную вектор-функцию v(x, t) , для которой найдется определенная в том же цилиндре скалярная вещественная функция P (x,t) такая, что при некотором q > 1 будут выполнены следующие условия:
-
1) вектор-функции v(t) = v( ^ ,t) и P(t) = P ( • , t) являются непрерывными, как отоб- °
ражения v : [0,T] ^ S q , v : (0,T] ^ S 2 , P : (0,T] ^ W q 1 (Q) , и равенство (3) выполнено в S q ;
-
2) отображение v : (0, T) ^ S q непрерывно дифференцируемо и первое равенство (1) справедливо при всех t Е (0 ,T ) в S q ;
-
3) второе равенство (1) при (x,t) Е Q х (0, T] и равенство (2) выполняются в обычном классическом смысле.
Прежде чем сформулировать определение обобщенного решения задачи (1)–(3) опишем известную процедуру (см., например, [13]) перехода от задачи (1)–(3) к соответствующему интегральному уравнению. Предположим на некоторое время, что ajski ∈ C([0, T], W^) и пусть v(x,t) — решение задачи (1)-(3), q > 3. Подействовав на уравнение (1) проектором П и обозначив v(t) = nv(-, t) = v(^,t), v(0) = v(^, 0) = vo, перейдем от начально-краевой задачи (1)–(3) к задаче Коши в Sq0 для абстрактного параболического уравнения:
dv
— + A o v = П dt
- (v , V ) v + X j =i
dX j a j (v, >t) + b ( v, • ,€ )
=
П^
х
(v, t)
=
t E (0, T], v(0) = v o .
Из результатов [11, 13] теперь следует, что всякое решение v( - ,t) задачи (1)-(3) удовлетворяет интегральному уравнению
v ( t ) = e tA 0 v 0 +
t j e—t-T)Ao^\v(t),t] o
dT = e tA 0 v o + l 0 = N(v)](t),
где l 0 понимается как предел в S q o интеграла I h при h ^ 0 .
Действительно, из определения решения задачи (1)–(3) вытекает, что при любом h E (0,T) справедливо соотношение ф \ v ( t ) ,t,шt ] E C (\ h, T ],Sq o ) • Отсюда согласно [13, лемма 23.1] следует равенство
v ( t ) = e -t- hA v ( h )+ I h , t>h.
Далее, в силу неравенства Гельдера существует постоянная c > 0 , при которой для всех к 6 m и v E C (\0,T], S p o ) выполнены оценки
Hajkl(v(t), ^Пс ([0,T],Sp0/k) 6 ckvkC ([o,T],Sp0), kbkl(v(t), •,t)kC ([0,T],Sp0/k) 6 ckvkc ([0,T],Sp0) •
Из этих оценок и оценок (9), (10) работы [1], следует существование такой константы c i > 0 , что при всех t E [0, T] и h i , h 2 E (0,t) справедливы неравенства
h 2
j e. ( T)A0^\v(t),t, шт] dT h1
h 2
- 3 ( m- 1) - 1
(t — т) 2 qo 2 dT h1
S q0
k v k m ([0 ,T ] ,S q 0 ) + 1
= c i
1 - 3 ( m- 1) 1 - 3 ( m- 1)
(t — h x ) 2 2 q o — (t — h 2 ) 2 2 p o
( kv k m ([0 ,T ] ,S q0
Учитывая определение решения задачи (1)–(3), сильную непрерывность полугруппы e -tA и неравенство (9) из [1], в (5) можно перейти к пределу при h ^ 0 по норме S q o , так что равенство (4) обосновано.
В пространстве C ([0, T ], S q o ) рассмотрим оператор N ti , который определен на вектор-функциях v(t) E C (\0,T],S q o П W^^ ) и действует по правилу, предписанному правой частью равенства (4). Тот факт, что образ N ti лежит в пространстве C ([0, T ], S q o ) вытекает из [13, лемма 23.1] и рассуждений данной статьи, использовавшихся при обосновании формулы (4). С помощью оценок (9), (10) из [1] и неравенства Г¨ельдера устанавливается, что оператор N ti непрерывен не только относительно аргумента v E C ([0, T ] , S q o ) , но
и относительно параметров a jk' Е C([0,T ], L ^ ) , в связи с чем будем рассматривать его на всем пространстве C([0,T],S q o ) в условиях п. 1 ° .
Определение. Обобщенным решением задачи (1)-(3) на участке t Е [0, T] называется трехмерная вещественная вектор-функция v ( t ) = v(>t) Е C([0, T ] , S q o ) , удовлетворяющая равенству v — N ^ (v) = 0.
Предложение 1. Существует такое положительное число T q 6 T , что задача (1)-(3) имеет единственное обобщенное решение u(x,t) Е C([0, T q ],S q o ).
C Не нарушая общности, будем считать m > 2 . Обозначим через U q шар пространства S q o с центром v q единичного радиуса. Пусть положительные числа M q , M i , L q и L i 1 2
удовлетворяют при любых w, w,w Е U q следующим условиям:
XI || n [ a j (w ’ • ’ • ) w j w ]|| c ( [0 ,T ] ,S /m ) 6 M 1 ’
1 6 j 6 3
k n b Q (w , > Alic ( [Q ,T ] ,S q0/m ) 6 M 2 ,
X 11 П [aj ( w ’ • , • ) — 1 6 j 6 3
w j w j
a j (w , • , • ) + го j x 1
V И C ( [Q ,T ] ,S q0/m)
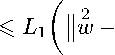
w 1
S q0
I s
+ max a j' — j,`,s
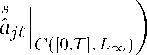
11 ” '■ ^ - b”(W' '■ 11C(M.Sp„/m) 6 L2 ( 11 W - W11 S^ • ss
Здесь вектор Qj (w, •, •) получен из aj(w, •, •) заменой функций a j'(x,t) на a j'(x,t) Е C([0,T],L^). Выберем теперь Tq Е (0,T] столь малым, чтобы выполнялись неравен- ства
11 (e 0 I )v 0 11 C ( [O ,T o ] ,S pO ) < 2
-
< M1 70 e M2T01-e2 \
V 1 — в1 1 — в2 /
/ LT - i + L 2 T0 1-e 2 A < 1
у 1 — в1 1 — в2 / где c — та же константа, что в оценках (9), (10) из [1], в1 = 3(т|0~) +1 ’ в2 = 3(1250™). Отметим, что существование Tq, удовлетворяющего первому из этих неравенств, следует из сильной непрерывности полугруппы e-tAo. Обозначим теперь через V шар пространства C([0,Tq],SPo) с центром vq единичного радиуса. Напомним, что обобщенным решением задачи (1)-(3) на временном участке t Е [0, Tq] по определению является вектор-функция v Е C([0,Tq],Sqo), удовлетворяющая при t Е [0,Tq] интегральному уравнению
v(t) = e
t tAovo + /e-(t-T)Aoи| X ^-aj(v,-’Т) 0 116j63 8xj
+ b o (v, • ’Т) — (v, V )vj>dT = [N(v,a)](t).
Докажем, что оператор N преобразует шар V в себя и является сжимающим. В силу неравенств, выписанных в предыдущей части доказательства предложения, а также
1 2 1 2
оценок (9) при к = 0 , (10) из [1] при всех v,v,v G V, a, a, a G C ([0, T],L ^ ) , t G [O,T o ] , имеем
|| [N (v,a)](t) - v o | S qo 6 | (e —tA o - 1 )v o | S qo + c j M ( t - т ) —в 1 + M 2 ( t - т ) —e 2 ]dr 6 1, (8) o
|| N(V,a) - N (V.A) | s
6 Я (t - т) —e ( l 1 | V o
- V Us
S q0
t
+ Il a - a IL || V 11^ ) dT + jL 2 (t - T ^^ H V - V Ilsq 0 /m dT o
/ cL1 r-p 1 — e i
6 1 - в 1 T 0
V v | C ([O ,T o ] ,L p 0 ) + || a a | C ([O ,T o ] ,L M ) | v | C ([O ,T o ] ,S q 0 )
cL2 ml— 8 2 11 2 111 1 i1 2 1 11 11 2 111
' | ,' T 0 || v - v | C ([O ,T o ] ,S po ) 6 2 || v - v | C ([O ,T o ] ,S qo ) + c 1 || a - a | C ([O ,T o ] ,L ^ ) •
Если v , a столь гладки, что выражение, заключенное в фигурной скобке в (7), принадлежит C ([O,T o ],S q o ) ,то N (u, a) G C ([0, T o ],S q o ) (см., например, [13, лемма 2.3]). Продолжая v G C ([0, T], S qo ) , a G C ([0, T], L ^ ) нулем за боковую границу цилиндра Q и аппроксимируя эти продолжения гладкими по x средними по Соболеву в силу оценки (9) заключаем, что при v G V , N (u, a) G C ([0, T o ],S q o ) . Теперь из оценок (8), (9) следует, что N (v,a) в шаре V является сжатием, а потому задача (1)–(3) имеет в этом шаре обобщенное решение.
Единственность обобщенного решения доказывается аналогично. Конкретнее, если V (t) , i = 1, 2, — два различных решения, то найдутся t 1 ,t 2 G [0,T O ) , t 1 < t 2 , такие, что V(t 1 ) = V(t 1 ) = V 1 , V(t) = V(t) , t G (t 1 ,t 2 ) , k- V(t) - V 1 k s qo 6 1 , t G [t 1 ,t 2 ] . Рассматривая теперь уравнение (7) с заменой V o на V 1 на участке t G [t 1 , t 2 ] и повторяя проведенные рассуждения, найдем такое T 1 G (t 1 ,t 2 ] , что определенный правой частью этого уравнения оператор (см. N ) в шаре V 1 = {v : Hv^c ([ t 1 ,T 1 ] ,s qo ) 6 1 } является сжатием. Отсюда на основании принципа сжатых отображений приходим к противоречию с неединственностью решений. Предложение 1 полностью доказано. B
4 ° . В этом пункте сформулируем и докажем лемму 1 работы [1] (см. введение). Доказательство следует пути, указанному в [2], и базируется на результатах и методах работ [2, 3, 14].
Лемма 2. Для любых чисел ^ G (0,1] и q > 3 найдется число y = Y(q, ^) G (0,1), при котором сужение проектора П на пространство вектор-функций C ^ (^) является ограниченным оператором из C ^ (^) в Sq' 1 .
Непосредственному доказательству леммы предпошлем определения моментной и аппроксимационной шкал, а также формулировку интерполяционной теоремы И. Б. Симоненко ( см. [2, 3]) .
Пусть B o , B , B 1 — тройка банаховых пространств, причем имеют место непрерывные вложения B 1 С B o , B С B o , пусть Y o > 0 , 7 1 > 0 , Y o + Y 1 = 1 .
Пространство B аппроксимационно разделяет пространства B o и B 1 в отношении 7 o : 7 1 , если для каждого x G B существует вектор-функция x(A) , A G [1, го ) , удовлетворяющая условиям:
-
a) x(A) 6 B 1 ;
-
б) ||x - х(А) к во 6 cA '" к х к в ;
-
в) | х(А) | в 1 6 cA Y 1 | х | в , где C — не зависящая от x постоянная.
Пространство B моментно разделяет Во и Bi в отношении Yo : Y1, если Bi С Во и для каждого x ∈ B1 выполняется оценка kxkB 6ckxkγB10kxkγB01
с независящей от x постоянной c .
Теорема (Интерполяционная теорема И. Б. Симоненко) . Пусть B o , В , B i , B' o , В', В '1 — банаховы пространства, причем B аппроксимационно разделяет B o и B 1 в отношении y , B ' моментно разделяет B ' и B 11 в отношении 7 ' , причем Y > Y ' • Пусть A 6 Hom(B o , B o ) и сужение А | в 1 6 Hom(B 1 , B 1 )• Тогда A|b 6 Hom(B, B ' ).
Обозначим через W q1 , q > 3 , подпространство пространства W q 1 (Q) трехмерных вектор-функций, определенных на Q , соленоидальных и имеющих на S равную нулю нормальную компоненту:
W q1 = Пи 6 W q1 (Q) : div u = 0, u n i s = 0O.
Предложение 2. Пространство W q1 аппроксимационно разделяет пространства S q
◦ 2
и S q .
◦ 2
C Отметим вначале, что имеют место вложения S q ⊂ S q и W q 1 ⊂ S q . Первое из них очевидно, второе следует из [3, леммы 5.2]. Докажем теперь, что для тройки пространств
◦ 2
S q , W q 1 , S q выполнены, сформулированные в начале настоящего пункта, условия a)–в).
Пусть u 6 Wq1. Тогда в силу леммы 6.2 монографии [12] существует векторное поле vo на Q такое, что div vo = 0, rot vo = u, von|s = 0, и выполнена оценка kv0 kWq2 (Ω) 6 ckukWq1 (Ω) ,
где c не зависит от u .
Возьмем теперь произвольный кусок S1 поверхности S , ограниченный контуром l. По формуле Стокса j vo dl = jrotn vo ds = j un ds = 0,
l
S 1
S 1
где rot n v o — нормальная составляющая вектора rot v o . Отсюда следует, что на поверхности S существует функция ^(s) 6 C 1 (S) ( s — локальные координаты поверхности) такая, что
V s ^ = v o .
Обозначим через p(x) расстояние точки x 6 Q до S, а через Qh0, ho > 0, — погранслой шириной ho : Qh0 = {x 6 Q : p(x) < ho}. Число ho будем считать столь малым, что нормали к S в Qh0 не пересекаются. Пусть ^(т) — бесконечно дифференцируемая при т 6 [0, со) функция такая, что 0 6 ^(т) 6 1
и
^ (т ) = I
1,
0,
0 6 т 6 2 , т > 1.
В погранслое Qh0 введем криволинейные координаты (s,p), где s(x) = (s1,s2) — точка поверхности S, лежащая с x на одной нормали, p(x) — расстояние от x до s. Определим функцию
Ф(x) =
f ^ [s(x)M P (x)/h o ],
I о,
x € Q h o , x € ^Wo .
Легко (например, с помощью теоремы о неявной вектор-функции) показать, чт о в нашем случае функции s(x) и p(x) непрерывно дифференцируемы, поэтому Ф € C 1 (Q) .
Покажем теперь, что справедливы соотношения
V Ф(x o ) = V ^[s(x o )] = v o [s(x o )],
|Vф(x) - Vф(xo)| 6 c\x - xoHlvokc(Q), где x € Qh0, xo = (s(x), 0) € S и C — не зависящая от x и vo постоянная. Для доказательства этих соотношений, не умаляя общности, предположим, что начало O декартовой системы координат Ox1x2x3 принадлежит S, ось Ox3 направлена по внутренней нормали к S и точки x, xo находятся в малой окрестности O, причем s1(x) = x1, s2(x) = x2. Отсюда легко получается представление
V ф(x) = (^ V s i + V s 2^ ^ [ p (x)/ h o ]
∂S 1 ∂S 2
+ y[s(x)]^
V
p(x) =
V
^
[
s
(
x) (x)/ho] + y[s(x)] d^dpx)] e[s(x)]. Здесь e[s(x)] = /df[s(x)] df[s(x)] ∂s1 ,∂s2 и мы, не умаляя общности, предполагаем, что поверхность S в малой окрестности O представлена уравнением x3 = f (xi,x2). Из (13) легко вытекают соотношения (11)-(12). Из (10), (12) и известной теоремы вложения С. Л. Соболева следует неравенство ||W(x) - W(xo)k 6 cp(x)kukwi, где x € Qh0, xo = (s(x), 0). Здесь и ниже c не зависит от x, u. Определим на Q векторное поле v(x) = vo(x) — VФ(x). Проведем «срезку» и «сглаживание» этого векторного поля, следуя рассуждениям В. И. Юдовича в лемме 5.2 [11]. Пусть функция nh(x) = 1 — ^[p(x)/h], x € Q. Введем на Q векторные поля uh = nhu + Vnh x v, u = rot v, uh,δ = j K5(x — y) uh(y) dy = j K5(x — y) uh(y) dy Ω R3 = rot / R3 K(x — y) nh(y) v(y) dy, x € Q, где Kδ— усредняющее по Соболеву ядро радиуса δ < h. Здесь ηh, u и v (а значит и uh) считаются продолженными с Q на R3 непрерывным образом. Для обоснования последнего равенства в (15) заметим, что для v при гладких vo и Ф оно очевидно, так как в этом случае согласно (14) Uh = rot(nhv), для наших же v G C(fi) оно получается отсюда путем замыкания. Обозначим для краткости uh,h2 через u0h. Легко видеть, что для u0hвыполняются условия а) ив) (А = h-1). Для обоснования соотношения б) воспользуемся неравенством Hu - UhkLq6Hu - UhkLq+ kuh - UhkLq ' В силу (10), (12) из [1] и теоремы вложения С. Л. Соболева имеет место оценка kv(x)k 6 cP(x)kukWi, x G fiho • (16) Используя представление (14), неравенство kVnhk < c1h 1, где c1 не зависит от h, и оценку (16), получим: Hu - uhkLq6||1 - nhkLq llukC + k|Vnh|vkLq (Qh) 6c^ 11UHWq1 ' Далее воспользуемся представлением Uh - Uh = j Kh2 (x - y)[nh(y)u(y) - nh(x)u(x)\ dy Ω + j Kh2 (x - y)Vnh(y) x v(y) dy - Vnh x v = wi + W2 + W3. Ω Легко получаем оценки: IHle 6 C (Hukeh + Hukeyh2Y) , где 0 < y < 1 - |, kw2kLq 6 k∇ηh × vkLq(Ω2h) 6 ch1/q kukWq1,(20) IW HLq = HW3 HLq (Qh) 6 ch1/1 HukWql • Из соотношений (17)–(21) и теоремы вложения С. Л. Соболева следует оценка ku - u0hkLq 6 chβ kukWq1, где в = min(1/q, 2y), c — не зависящая от u постоянная. Итак, свойство б), а с ним и предложение полностью доказаны. B о 2^ C Доказательство леммы 1. Как известно [11, 13], пространство Sqмоментно о 2^1 разделяет Sq и Sq , где 0 < 5 < 5i 6 1, в отношении ^- : (1 - ^-). Рассмотрим две тройки о 2 о 28 о 2 пространств Sq, Wq1, Jqи Sq, Sq, Sq. Из предложения 2, первого предложения настоящего доказательства и интерполяционной теоремы И. Б. Симоненко следует существование такого числа 52 G (0,1), что имеет место непрерывное вложение о Wq1⊂ S 2δ2 q о 2 Обозначим через C банахово пространство, полученное замыканием финитных в Ω о2 трехмерных вектор-функций по норме C2 . Как известно, при u ∈ C , справедливо представление u = Πu + ∇ϕ, Πu · n|S = 0, div Πu = 0, где ϕ — решение задачи Неймана 4ш = div u, I = 0. ∂u S о 2 о 2^2 Отсюда с помощью известных априорных оценок следует, что Π ∈ Hom C , Sq. Поэтому в силу (22) / о 2 о 2^2 \ Π∈Hom C ,Sq. (23) Рассмотрим теперь еще две тройки пространств трехмерных вектор-функций: Lq, о 2 о 2^ о 2^2 Cµ , C и Sq, Sq , Sq , где 0 < δ < δ2 . Нетрудно показать, что Cµ аппроксимационно о2 разделяет Lq и C . Как отмечалось выше, Π ∈ Hom(Lq, Sq) (см. [11]). Отсюда, из (23) и интерполяционной теоремы И. Б. Симоненко следует существование такого δ0 = δ0(q, µ), о 2^0 что П|см G Hom (C^, Sq ). B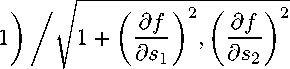
Список литературы О взаимосвязи двух классов решений уравнений Навье - Стокса. II
- Левенштам В. Б. О взаимосвязи двух классов решений уравнений Навье -Стокса//Владикавк. мат. журн.-2010.-Т. 12, вып. 3.-С. 56-66.
- Симоненко И. Б. Обоснование метода усреднения для задачи конвекции в поле быстро осциллирующих сил и для других параболических уравнений//Мат. сб.-1972.-Т. 87 (129), № 2.-С. 236-253.
- Симоненко И. Б. Метод усреднения в теории нелинейных уравнений параболического типа с приложением к задачам гидродинамической устойчивости.-Ростов н/Д.: Изд-во РГУ, 1989.-112 с.
- Левенштам В. Б. Одно свойство проектора $\Pi$ гидродинамики//Комплексный анализ, дифференциальные и интегральные уравнения.-Эллиста, 1990.-С. 89-96.
- Левенштам В. Б. Обоснование метода усреднения для задачи конвекции при высокочастотных вибрациях//Сиб. мат. журн.-1993.-Т. 34, № 2.-С. 92-109.
- Левенштам В. Б. Асимптотическое разложение решения задачи о вибрационной конвекции//Журн. вычислительной математики и мат. физики.-2000.-Т. 40, № 9.-С. 1416-1424.
- Levenshtam V. B. Asymptotic integration on initial boundary problem for Navier-Stokes system with a rapidly oscillating mass force//Russian J. of Math. Physics.-2005.-Vol. 12, № 1.-P. 40-48.
- Левенштам В. Б. Асимптотическое интегрирование параболических задач с большими высокочастотными слагаемыми//Сиб. мат. журн.-2005.-Т. 46, № 4.-С. 805-821.
- Левенштам В. Б. Обоснование метода усреднения для дифференциальных уравнений, содержащих быстроосцилирующие слагаемые с большими амплитудами//Изв. РАН. Сер. мат.-2006.-Т. 70, № 2.-С. 25-56.
- Левенштам В. Б. Некоторые вопросы теории усреднения параболических уравнений с большими высокочастотными слагаемыми//Докл. АН.-2006.-Т. 411, № 3.-С. 302-305.
- Юдович В. И. Метод линеаризации в гидродинамической теории устойчивости.-Ростов н/Д.: Изд-во РГУ, 1984.-192 с.
- Ладыженская О. А. Математические вопросы динамики вязкой несжимаемой жидкости.-М.: Наука, 1970.-288 с.
- Красносельский М. А., Забрейко П. П., Пустыльник Е. И., Соболевский П. Е. Интегральные операторы в пространствах суммируемых функций.-М.: Наука, 1966.-500 с.
- Быховский Э. Б.,Смирнов Н. В.Об ортогональных разложениях пространства вектор-функций, квадратично суммируемых по данной области//Тр. МИАН СССР.-1960.-Вып. 59.-С. 6-36.


