О заблуждениях в современной логике
Автор: Кулик Б.А.
Журнал: Онтология проектирования @ontology-of-designing
Рубрика: Общие вопросы формализации проектирования: онтологические аспекты и когнитивное моделирование
Статья в выпуске: 1 (55) т.15, 2025 года.
Бесплатный доступ
В статье обсуждается несостоятельность трёх «бесспорных» положений в современной логике: о противоречивости понятия «множество»; о безусловной необходимости аксиом в логике; о безошибочности силлогистики. Первое заблуждениеие преодолевается предложением использовать в основаниях логики алгебру множеств в том варианте, который изложен в книге Р. Куранта и Г. Роббинса «Что такое математика?». Второе заблуждениеие преодолевается с помощью вывода известных законов алгебры множеств, которые соответствуют законам классической логики, методом перебора вариантов. Третье заблуждениеие преодолевается построением математической модели полисиллогистики, в основе которой лежат законы алгебры множеств. Новизна предложенной модели рассуждений заключается в том, что в неё помимо посылок вводятся ограничения, нарушение которых свидетельствует о некорректности рассуждения. Данная модель позволяет расширить аналитические возможности логического анализа и выявлять некорректности традиционной силлогистики, к которым, в частности, относится признание «неправильными» модусами некоторых правильных рассуждений. Формулируются и обосновываются новые законы алгебры множеств: закон парадокса, условие непустого пересечения и закон существования.
Силлогистика, полисиллогистика, логический анализ, алгебра множеств, аксиомы, граф включений, закон парадокса, закон существования, логические ошибки
Короткий адрес: https://sciup.org/170208811
IDR: 170208811 | УДК: 004.83+162.2 | DOI: 10.18287/2223-9537-2025-15-1-11-23
Текст научной статьи О заблуждениях в современной логике
В утверждении о том, что логика лежит в основе всей математики, есть одно исключение. Об этом исключении написано в книге Р. Куранта и Г. Роббинса [1], первое издание которой вышло в 1941 году. Речь идёт о математической системе, которая авторами книги названа алгеброй множеств . Исключительность алгебры множеств выражается в том, что её законы, как считают авторы книги, можно обосновать без аксиом, на основе определения отношения включения и операций с множествами. Приведённые в этой книге 26 законов алгебры множеств полностью соответствуют законам классической логики. Это означает, что для обоснования законов классической логики нет необходимости в аксиомах .
В настоящей статье рассмотрены три заблуждения в современной логике: о противоречивости понятия «множество»; о безусловной необходимости аксиом в логике; о безошибочности силлогистики. Каждое из данных заблуждений преодолевается с использованием средств элементарной математики. В основе этих средств лежит обоснование законов алгеб- ры множеств с помощью перебора вариантов и построение математической модели полисиллогистики на основе законов алгебры множеств.
1 О противоречивости понятия «множество»
О противоречивости понятия множества отмечено в книгах Э. Мендельсона [2, 3]. «Поскольку семантические понятия носят теоретико-множественный характер, а теория множеств, по причине парадоксов, представляется в известной степени шаткой основой для исследований в области математической логики, то многие логики считают более надёжным синтаксический подход, состоящий в изучении формальных аксиоматических теорий с применением лишь довольно слабых арифметических методов».
В учебниках логики такая явная негативная оценка понятия множества не встречается, а в некоторых учебниках [4-6] содержатся начальные сведения о множествах. При анализе свойств понятий во многих учебниках используются не множества, а «объёмы» и схемы в виде кругов Эйлера; для обоснования правильности модусов силлогистики используются модельные схемы [4, 6], семантические схемы [7] и диаграммы Венна [8], т.е. сущности, которые являются наглядными представлениями математических соотношений между множествами.
В аксиоматической теории множеств отношение принадлежности ( ∈ ) является основным. Одна из аксиом теории множеств (аксиома пары [9, 10]) предписывает использовать множества в качестве элементов. Это означает, что в теории множеств, если не вводить ограничения в виде других аксиом, допустимы такие выражения, как «множество всех множеств» и «множество, являющееся элементом самого себя» (самоприменимое множество), которые и вызывают парадоксы. В алгебре множеств отношение принадлежности – вспомогательное и служит лишь для описания конкретных множеств или для определения того, что данный элемент принадлежит определённому множеству. И в ней не предписано отождествлять элемент и множество.
Основным (системообразующим) в алгебре множеств является отношение включения. Это отношение используется в основных законах алгебры множеств. Его «самопримени-мость» ( A ⊆ A ) является одним из законов алгебры множеств и не влечёт парадоксов.
Иногда алгебру множеств отождествляют с наивной теорией множеств [11]. Однако такое отождествление не вполне корректно. В этой книге излагается один из вариантов аксиоматической теории множеств. А в книге [1] алгебра множеств – это математическая система с определёнными операциями (пересечение, объединение, дополнение) и отношениями (принадлежность, включение, равенство).
В современной математике термину «алгебра множеств» часто придают смысл, существенно отличающийся от его значения, предложенного в [1]. С точки зрения разработанной значительно позже теории алгебраических систем [12] алгебра множеств – это система, в которой нет отношений. Такое понимание алгебры множеств изложено в [13] и во многих руководствах по дискретной математике. В результате такого подхода аналитические возможности алгебры множеств весьма ограничиваются. Чтобы расширить эти аналитические возможности, приходится выбирать не алгебру множеств, а такую «шаткую основу» (Э. Мендельсон) как аксиоматическая теория множеств [2, 3].
Выбирая в качестве средства для анализа повседневной жизни аксиоматическую теорию множеств, приходится действовать по правилам, которые для этой повседневности не предназначены. Речь идёт об актуальной бесконечности [9]. Помимо актуальной бесконечности в математических доказательствах часто используется потенциальная бесконечность , законы которой соответствуют законам конечных множеств, и с помощью которой доказаны многие теоремы математического анализа и многие законы физики и техники.
С точки зрения потенциальной бесконечности натуральный ряд чисел 1, 2, 3, 4, … – это конечный ряд, о котором известно только, что он не имеет предела. Относительно любого числа M в этом ряду существует и может быть задано число, большее, чем M. Для этого достаточно увеличить M всего лишь на единицу.
Если речь идёт о линии (пусть это будет отрезок прямой линии), то с точки зрения потенциальной бесконечности этот отрезок состоит не из бесконечного количества точек, а из конечного количества отрезков , длина которых уменьшается так, что она может оказаться меньше любой заранее заданной величины. В соответствии с этим увеличивается и количество отрезков, покрывающих данный отрезок. Но при этом количество покрывающих отрезков остаётся конечным.
Что касается точек, то они присутствуют в потенциальной бесконечности как границы интервалов. При разбиении отрезка на конечное количество малых отрезков количество точек, определяющих границы интервалов, тоже конечно. Если же предположить, что интервал состоит только из точек, то тем самым можно перейти к актуальной бесконечности с её законами, не совместимыми с законами конечных множеств.
В качестве примера можно сравнить мощности множеств целых чисел с точки зрения разных бесконечностей. Пусть даны ряды целых ( N) и чётных ( N г ) чисел:
N : 1, 2, 3, 4, . . . , M , . . .
N г : 2, 4, 6, 8, . . . , 2 M , . . .
С точки зрения актуальной бесконечности при сравнении этих рядов соблюдается принцип взаимно однозначного соответствия : каждому числу ряда N соответствует определённое и единственное число из ряда N 2. Отсюда следует вывод о равенстве мощностей множеств N 2 и N .
С точки зрения потенциальной бесконечности, в которой предполагается, что любое продолжение ряда представлено конечным множеством, видно, что не соблюдается соотношение строгого включения N 2 с N . Нетрудно убедиться, что в нижнем ряде при любой конечной фиксации ряда присутствуют числа, которые не содержатся в верхнем ряде. Например, если ряд N завершается числом M , то в ряде N г присутствует число 2 M и некоторые другие числа (2 M - 2, 2 M - 4 и т.д.), которые отсутствуют в ряде N . Отсюда ясно, что при таком сравнении соотношение N 2 с N не выполняется.
Поэтому с точки зрения потенциальной бесконечности правильным является расчёт соотношения между количеством всех чисел ряда N и количеством всех чётных чисел этого ряда. Нетрудно убедиться, что если ряд N в какой-то момент времени завершается числом M , то количество содержащихся в нём чётных чисел K зависит от того, является ли число M чётным или нечётным. Если M чётное, то K = М /2, если же M нечётное, то K = ( М - 1)/2.
Полученные соотношения позволяют рассчитать относительную мощность чётных чисел в ряде всех целых чисел: k = К / М . Для чётного M относительная мощность k = 1/2, для нечётного k = ( М - 1)/2 М = 1/2 - 1/2 М .
Используя это равенство, можно доказать, что при неограниченном возрастании M число k в точности равно 1/2 для чётного M и будет неограниченно приближаться к 1/2 для нечётного M , так как число 1/2 М уменьшается неограниченно по мере возрастания числа M .
Этот результат не соответствует утверждению о равномощности чисел натурального ряда и ряда чётных чисел, обоснованному с точки зрения актуальной бесконечности. Можно предположить, что многие «нестандартные» свойства актуальной бесконечности (теорема Банаха - Тарского о равновеликом удвоении шара, парадоксы теории вероятностей и математической статистики [14] и т.д.) обусловлены тем, что при обоснованиях «парадоксальных» результатов используются свойства и соответствия, которые не подтверждаются при рассмотрении этих свойств с точки зрения потенциальной бесконечности.
2 Обоснование законов алгебры множеств без аксиом
Основные понятия алгебры множеств подробно изложены в разделе «Алгебра множеств»1 [1], где перечислено 26 законов алгебры множеств. Они приведены здесь для того, чтобы получить возможность оценить их соответствие с законами классической логики и сравнить с новыми законами, формулировки и обоснования которых приведены в разделе 4. Пусть A , B и C - произвольные множества, U - универсум рассуждения и 0 - пустое множество. Тогда справедливы следующие законы.
1 ) A с A.
-
2 ) Если A с B и B с A , то A = B .
-
3 ) Если A с B и B с C , то A с C .
-
4 ) 0 с A.
-
6 ) A о B = B о A.
-
8 ) A о ( B о C) = ( A о B ) о C.
-
10) A о A = A.
-
12) A n ( B о C) = ( A n B ) о ( A n C).
-
14) A о 0 = A.
-
16) A о U = U .
-
5) A с U .
-
7) A n B = B n A .
-
9) A n ( B n C ) = ( A n B ) n C .
11) A n A = A .
13) A о ( B n C) = ( A о B ) n ( A о C)
15) A n U = A .
17) A n 0 = 0 .
-
18) A с B эквивалентно A о B = B и эквивалентно A n B = A .
-
19) A о A = U .
-
21) 0 = U .
-
20) A n A = 0 .
-
22) U = 0 .
-
-
23) A = A .
-
24) A с B эквивалентно B с A .
-
25) A о B = A n B . 26) A n B = A о B .
Закон 2 используется для доказательства равенства множеств [15]. В [3, 15] закон 3 называют законом транзитивности включения множеств, законы 12 и 13 - законами дистрибутивност и, закон 23 - законом двойного дополнения, закон 24 - законом контрапозиции, а законы 25 и 26 - законами де Моргана; в [3, 5] закону 19 соответствует закон исключенного третьего, а закону 20 - закон непротиворечия.
Проверить справедливость этих законов можно с помощью перебора вариантов соотно- шений между множествами [1]. На рисунке 1 изображена диаграмма Венна, с помощью которой можно выразить все возможные соотношения между двумя множествами A и B с учётом их общего универсума U.
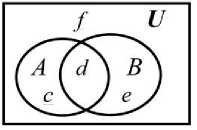
Рисунок 1 - Диаграмма Венна для двух множеств
На рисунке области c, d, e и f не пересекаются друг с другом, а их объединение равно U. Тем самым они образуют разбиение универсума. Это позволяет использовать эти области в качестве элементов множеств U, A и B. Тогда для доказательства законов алгебры множеств можно взять за основу следующие исходные данные: U = {c, d, e, f}; A = {c, d}; B = {d, e}.
Используя эти исходные данные, можно доказать закон 25: A о B = A n B . Для этого в соответствии с определениями операций алгебры множеств [1] последовательно можно вы- полнить следующие вычисления.
1) A о B = { c , d , e }; 2) A U B = {f}; 3) A = { e , f }; 4) B = { c , f }; 5) A n B = {f};
-
6) Сравнивая 2 и 5, можно получить: A о B = A n B .
Вычисления подтверждают справедливость закона 25. Однако этого недостаточно, т.к. необходимо проверить этот закон для всех возможных вариантов соотношений между множествами A и B . Эти варианты можно получить, если последовательно исключать элементы c , d , e и f и их сочетания из универсума U . Нетрудно убедиться, что таких вариантов 16.
-
1) U = { c , d , e , f }; A = { c , d }; B = { d , e }.
-
2) U = { c , d , e }; A = { c , d }; B = { d , e }.
-
3) U = { c , d , f }; A = { c , d }; B = { d }.
-
4) U = { c , e , f }; A = { c }; B = { e }.
-
5) U = { d , e , f }; A = { d }; B = { d , e }.
-
6) U = { c , d }; A = { c , d }; B = { d }.
-
7) U = { c , e }; A = { c }; B = { e }.
-
8) U = { c , f }; A = { c }; B = 0 .
-
9) U = { d , e }; A = { d }; B = { d , e }.
-
10) U = { d , f }; A = { d }; B = { d }.
-
11) U = { e , f }; A = 0 ; B = { e }.
-
12) U = { c }; A = { c }; B = 0 .
-
13) U = { d }; A = { d }; B = { d }.
-
14) U = { e }; A = 0 ; B = { e }.
-
15) U = f }; A = 0 ; B = 0 .
-
16) U = 0 ; A = 0 ; B = 0 .
Например, можно доказать справедливость закона де Моргана для варианта 8.
-
1) A . B = { c }; 2) A U B = f }; 3) A = f j) B_ = { c , f}; 5) A n B = { / };
-
6) Сравнивая 2 и 5, можно получить: A о B = A n B .
Можно рассмотреть некоторые варианты доказательства закона контрапозиции. В этом законе соотношение A о B является обязательным условием, поэтому необходимо учитывать те из 16 вариантов, в которых соблюдается это соотношение (5, 9, 10, 11, 13, 14, 15, 16).
В качестве примера этот закон можно доказать для варианта 5.
-
1) Проверяется, что A о B : { d } о { d , e }; 2) A = { e , f }; 3) B = {f};
-
4) Проверка показывает, что B о A .
Закон контрапозиции подтверждается и для других семи вариантов. Если рассмотреть варианты соотношений между множествами, в которых не соблюдается A о B , то можно убедиться, что для множеств B и A соотношение B о A также не соблюдает с я во всех этих вариантах. Тем самым подтверждается равносильность соотношений A о B и B о A .
Предложенный метод доказательства, в котором используется простой перебор вариантов, может показаться трудоёмким. Например, чтобы доказать законы дистрибутивности, в которых участвуют три множества, потребуется рассмотреть 256 вариантов в каждом случае. Можно сократить число вариантов, если для доказательства этого закона воспользоваться другими, менее трудоёмкими при обосновании, законами алгебры множеств. Идею такого доказательства законов дистрибутивности с использованием закона 2 можно найти в [15]. Преимущество этого метода в том, что он позволяет показать возможность строгого доказательства законов алгебры множеств без аксиом. Тем самым можно получить непротиворечивую систему, в которой выводятся основные законы классической логики.
3 Математическая модель полисиллогистики
Полисиллогистика – это математическая система рассуждений, в которой задано произвольное число неструктурированных относительно друг друга суждений силлогистики [4, 5] в качестве посылок, а также сформулированные здесь ограничения. В задачи полисиллогистики входят вывод заключений и распознавание некорректностей в рассуждении.
В основе силлогистики, созданной Аристотелем, лежат четыре типа суждений [4, 5]:
-
A : Все P есть Q , пример: «Все крокодилы – рептилии».
-
I : Некоторые P есть Q , пример: «Некоторые студенты – спортсмены».
-
E : Все P не есть Q , пример: «Все жирафы – не земноводные».
-
O : Некоторые P не есть Q , пример: «Некоторые мои коллеги не любят критику».
-
A , I , E , O – общепринятые обозначения типов суждений, при этом типы A и E называются общими суждениями, а типы I и O – частными .
Пример силлогизма .
-
1 -я посылка : Все кустарники – не животные. 2 -я посылка : Все кустарники – растения.
Заключение : Некоторые растения не являются животными.
Это пример правильного силлогизма. Он состоит из двух общих посылок (типы E и A ) и частного заключения (тип O ). В силлогистике для распознавания правильных силлогизмов необходимо знать, из каких типов суждений они состоят и какова их структура. Структура силлогизма определена с помощью четырёх типов фигур с номерами 1, 2, 3, 4. Варианты силлогизмов с указанием типов содержащихся в них суждений и номеров соответствующих фигур называется модусами силлогизма . Например, приведённый силлогизм соответствует модусу EAO фигуры 3.
Всего можно построить 256 различных модусов, из них число правильных модусов невелико, причём в разных учебниках логики они различны: 15 в [8], 19 в [5], 24 в [4, 6, 7]. Чтобы определить, правильно ли заданное рассуждение, надо сравнить это рассуждение с одним из этих списков правильных модусов. Такой способ анализа правильности рассуждений нередко приводит к неоднозначным результатам. Недостатки силлогистики подробно рассмотрены в [16]. Здесь перечислены некоторые из них и предложены способы их устранения.
Недостаток 1: В силлогизме предусмотрено только две посылки и одно заключение. Предлагается одним общим методом анализировать системы с любым числом посылок, для которых возможны более одного следствия или заключения. Тем самым можно перейти к общему методу анализа рассуждений с произвольным числом посылок.
Недостаток 2: В силлогистике все термины не должны соответствовать пустому множеству. В противном случае некоторые правильные модусы силлогизма окажутся ошибочными. Этот запрет ограничивает возможности анализа, т.к. не позволяет проверить существование анализируемых объектов (с точки зрения математики множество существует, если для данных посылок доказано его неравенство пустому множеству). Предлагается не запрещать равенство терминов пустому множеству, но при этом предусмотреть в рассуждении помимо посылок ограничения, в составе которых могут быть запреты равенства некоторых объектов пустому множеству.
Недостаток 3: В силлогистике при изменении порядка посылок часто образуются неправильные модусы силлогизма, в силу чего изменение порядка посылок в силлогистике запрещено. Например, если в приведённом выше силлогизме переставить посылки, то полученный модус окажется неправильным. Если суждения этого силлогизма выразить в терминах математической логики, то перестановка посылок не повлияет на результат. В предлагаемой системе полисиллогистики этот запрет не имеет смысла.
На основе законов алгебры множеств можно построить систему логического вывода с учётом предложенных изменений. Типы суждений можно выразить в соотношениях алгебры множеств. Пусть термины P и Q в формулировках суждений соответствуют некоторым одноименным множествам. Тогда типам суждений будут соответствовать следующие выражения алгебры множеств:
-
A : P ⊆ Q ; I : P ∩ Q ≠ ∅ ; E : P ⊆ Q ; O : P ∩ Q ≠ ∅ .
С учётом этого для полисиллогистики предлагается следующая математическая м одель 2 . Пусть в универсуме U задана система множеств S i ( i = 1, 2, … , n ) и их дополнений Si без перечисления их элементов, при этом допускается возможность равенства некоторых из этих множеств пустому множеству или универсуму. В результате проведённого анализа некоторые из этих множеств могут оказаться равными друг другу. Для этой системы заданы логические посылки двух типов:
-
■ общие суждения заданы как соотношения включения между некоторыми из заданных множеств (например, S 2 ⊆ S 3 );
-
■ частные суждения , выражающие обязательность непустого пересечения некоторых пар множеств (например, S 2 ∩ S 6 ≠ ∅ ).
В этой системе можно установить два вида ограничений:
-
■ ограничения подмены термина (или двусмысленности) выражаются как недопустимость равенства некоторых пар множеств (например, S 2 ≠ S 4 );
-
■ ограничения пустоты выражаются как недопустимость равенства пустому множеству некоторых из заданных множеств (например, S 4 ≠ ∅ ).
В рассматриваемой модели в качестве одного из условий можно предусмотреть предполагаемое следствие , которое выражено в виде общего суждения.
С помощью этой модели рассуждений можно решать следующие задачи.
Задача 1: Найти следствия в виде соотношений включения между не заданными в условиях задачи парами множеств (выводятся следствия в виде новых общих суждений).
Задача 2: Проверить, нарушаются ли в данной системе ограничения подмены термина.
Задача 3: Если задано предполагаемое следствие, то проверить, выводится ли это следствие из заданных посылок. В случае отрицательного результата осуществляется поиск возможных посылок, добавление которых в модель рассуждений позволяет превратить предполагаемое невыводимое следствие в обычное следствие. Найденные варианты таких посылок являются абдуктивными заключениями .
Задача 4: Проверить, нарушаются ли в данной системе ограничения пустоты (проверяется отсутствие или наличие парадоксов в рассуждении).
Задача 5: Найти новые пары множеств, для которых доказывается непустое пересечение (выводятся заключения в виде новых частных суждений).
Задача 6: Установить, для каких множеств, помимо тех, что заданы в ограничениях пустоты, доказывается их безусловное неравенство пустому множеству.
Решения Задач 1 – 5 можно найти в [17]. Решение задач полисиллогистики удобно начать с построения графа включений.
Литерал – это обозначение множества или его дополнения, например, S 2 и S 2 .
Граф включений – это граф , на котором литералы представлены вершинами , а отношения включения между соответствующими множествами – дуги графа. Если, например, S 4 ⊆ S 2 , то на графе включений дуга направлена от литерала S 4 к литералу S 2 ( S 4 → S 2 ). Для упрощения на рисунках изображаются дуги от литерала к литералу.
Порядок действий при решении всех шести задач начинается одинаково.
-
1) строится граф включений для всех посылок;
-
2) применяется закон контрапозиции ко всем посылкам и дополняется граф включений.
Пример 1 . Этот пример взят из книги [18] с изменениями (термин «ростовщик» заменён на термин «мошенник» и добавлена шестая посылка). В примере демонстрируется ситуация,
-
2 Эта модель отличается от соответствующей модели в [17] тем, что в ней не используются аксиомы E -структур.
когда абсурд обусловлен не ошибками в логическом выводе, а незаметно присутствует в посылках. Даны посылки:
-
1) те, кто нарушает свои обещания, не заслуживают доверия;
-
2) все любители выпить очень общительны;
-
3) человек, выполняющий свои обещания, честен;
-
4) ни один трезвенник – не мошенник;
-
5) тому, кто очень общителен, всегда можно верить;
-
6) все честные люди – не мошенники.
Необходимо вывести новые общие суждения (Задача 1) и проверить существование мошенников, т.е. проверить соблюдается ли ограничение пустоты (Задача 4) для термина «мошенник».
Можно сформулировать посылки полисиллогизма в виде соотношений между следующими множествами: U – люди; S 1 – нарушающие обещания; S 2 – заслуживающие доверия; S 3 – любители выпить; S 4 – очень общительные; S 5 – честные; S 6 – мошенники. Тогда суждения Примера 1 можно выразить в виде следующих соотношений.
1) S 1 ⊆ S 2 ; 2) S 3 ⊆ S 4 ; 3) S 1 ⊆ S 5 ; 4) S 3 ⊆ S 6 ; 5) S 4 ⊆ S 2 ; 6) S 5 ⊆ S 6 .
Ограничение пустоты : S 6 ≠ ∅ .
Для упрощения решения задач граф включений рекомендуется изображать таким способом (см. рисунок 2): в верхней строке располагаются все позитивные литералы, в нижней – все негативные. Так исключается пропуск литералов, и на такой схеме можно легко выводить контрапозиции исходных суждений.
Для решения задачи необходимо применить закон контрапозиции и (при необходимости) закон двойного дополнения к выводимым посылкам.
-
7) S 2 ⊆ S 1 ; 8) S 4 ⊆ S 3 ; 9) S 5 ⊆ S 1 ; 10) S 6 ⊆ S 3 ; 11) S 2 ⊆ S 4 ; 12) S 6 ⊆ S 5 .
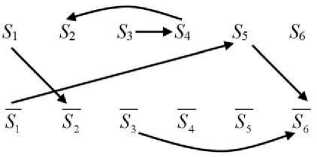
Рисунок 2 – Граф включений для посылок (Пример 1)
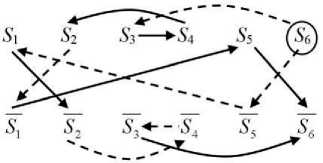
Рисунок 3 – Посылки и следствия (Пример 1)
Граф включений для посылок и их контрапозиций (изображены штриховыми линиями) представлен на рисунке 3. Из рисунка видно, что контрапозиции исходных суждений можно построить, используя правило: если исходное суждение соединяет пару литералов, то контрапозиция этого суждения соединяет противоположные литералы, при этом направление дуги изменяется на обратное.
На схеме можно найти начальные литералы, т.е. те, в которые не входит ни одна дуга. Для данной задачи это единственный литерал – S6. Возможны задачи, у которых нельзя найти начальные литералы, т.к. все пути в графе включений могут оказаться циклами. В по- лисиллогистике цикл означает, что все литералы, содержащиеся в нём, представляют равные друг другу множества [17].
Закон транзитивности позволяет утверждать, что если имеется путь от одного литерала к другому, то множество, соответствующее начальному литералу пути, включено в множество, соответствующее конечному литералу. Отсюда в обоих случаях получается S6 ⊆ S6 (все мошенники – не мошенники, что означает коллизию парадокса).
Если в Примере 1 исключить суждение 6 «все честные люди – не мошенники», то парадокс не появится, но при этом можно получить неожиданное следствие «все мошенники – честные», что не соответствует значению слова «мошенник».
4 Новые законы алгебры множеств
Необходимость в новых законах вызвана тем, что без них невозможно решение некоторых задач полисиллогистики. Первый закон назван законом парадокса.
-
( i ) Закон парадокса : если доказано, что X с X , то X = 0 .
Доказательство . Из определения операции дополнения следует, что в множестве X содержатся те и только те элементы универсума U , которые не являются элементами X . Пусть имеется элемен т b такой, что b ∈ X . В то же время из условия X ⊆ X следует, что элемент b содержится в X , т.е. по определению b ∉ X . Полученное противоречие можно разрешить единственным способом: X = ∅ . Конец доказательства .
Закон парадокса можно также доказать методом перебора, используя 16 вариантов возможных соотношений между множествами U , A и B . Проверка показывает, что соотношение A ⊆ A соблюдается только в вариантах 11, 14, 15, 16, т.е. в тех и только в тех, где A = ∅ .
К парадоксу также приводит следующая ситуация. Пусть в результате рассуждений оказалось, что некоторый объект A обладает свойством B и в то же время не обладает им. Например, не вызывает сомнения то, что Ахиллес догонит черепаху, но вместе с этим «доказыва е тся», что он не может её догнать. Это можно выразить в виде двух п осылок: A ⊆ B и A ⊆ B . Применив закон контрапозиции ко второй посылке, получается B ⊆ A . В то же время из A ⊆ B и B ⊆ A по закону транзитивности следует A ⊆ A .
Парадокс образуется и в том случае, когда свойствами объекта одновременно являются не контрадикторные , а контрарные сущности, когда для двух непустых множеств B и C выполняется отношение C ≠ B , но при этом C ⊆ B .
Пусть даны две посылки A ⊆ B и A ⊆ C . При этом свойства B и C являются контрарными, что можно выразить с помощью соотношения B ⊆ C . Можно использовать это соотношение в качестве третьей посылки. Тогда из A ⊆ B и B ⊆ C по закону транзитивности получается A ⊆ C . В итоге получается коллизия парадокса A ⊆ C и A ⊆ C , из чего следует A ⊆ A .
Второй новый закон алгебры множеств применяется для упрощения анализа частных суждений. Выражения для частных суждений типа S 2 ∩ S 6 ≠ ∅ не дают возможности непосредственно получать новые частные суждения, т.к. для этих выражений нельзя использовать законы транзитивности и контрапозиции. Поэтому предложено дать следующую формулировку для частных суждений:
-
( ii ) Условие непустого пересечения : a k с Х и a k с Y при условии a k ^ 0 равносильно выражению X ∩ Y ≠ ∅ .
Доказательство . Если α k ≠ ∅ , то существует элемент b такой, что b ∈ α k . Из α k ⊆ X и α k ⊆ Y следует, что b ∈ X и b ∈ Y , в силу чего справедливо X ∩ Y ≠ ∅ . Конец доказательства .
Третий новый закон предназначен для распознавания безусловно непустых множеств среди тех множеств системы, которые не заданы в ограничениях пустоты.
-
( iii ) Закон существования : если X ^ 0 и X с Y , то Y ^ 0 .
Доказательство . Поскольку X ≠ ∅ , то существует элемент b такой, что b ∈ X . Поскольку X ⊆ Y , то b ∈ Y . Следовательно, Y ≠ ∅ . Конец доказательства .
Этот закон по форме соответствует известному в логике правилу вывода ( modus ponens , MP ): если выводимы формулы A и A ⊃ B , то выводима формула B ( ⊃ – обозначение логической связки импликации). По сути, закон ( iii ) - это MP применительно к множествам.
Использование трёх новых законов можно показать на следующем примере.
Пример 2. В Пример 1 вносится следующее изменение: оставляя неизменным ограничение пустоты (S6 ≠ ∅), вторая посылка «все любители выпить очень общительны» преобразу- ется в более правдоподобное частное суждение «некоторые любители выпить очень общительны». Тогда вместо посылки S3 ⊆ S4 надо, используя закон (ii), ввести две посылки: αk ⊆ S3 и αk ⊆ S4 при условии αk ≠ ∅. В соответствии с этим можно построить граф включений (рисунок 4). Анализ этого графа позволяет получить следующие выводы.
-
1) На графе включений имеются три начальных литерала: S 6 , S 3 и α k .
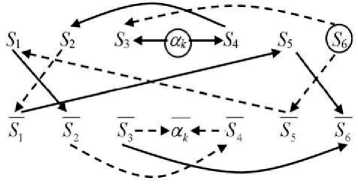
Рисунок 4 – Граф включений (Пример 2)
-
2) Из литерала S 6 (мошенники) исходят две ветви: S 6 → S 5 → S 1 → S 2 → S 4 → α и S 6 → S 3 . Это означает, что мошенники обладают следующими качествами: не честные, нарушающие обещания, не заслуживающие доверия, не общительные, любители выпить. Среди перечисленных свойств, в отличие от Примера 1, нет кон-
- традикторных, что означает отсутствие парадокса.
-
3) Из непустого литерала α k исходят две ветви: α k → S 4 → S 2 → S 1 → S 5 → S 6 и α k → S 3 .
По условию непустого пересечения получается, что непустое пересечение имеют пары лите- ралов, находящихся на одной из этих ветвей (например, S4 ∩S1 ≠ ∅, т.к. αk ⊆ S4 и αk ⊆S1 ), и пары литералов, содержащихся в разных ветвях, исходящих из αk (например, S6 ∩ S3 ≠ ∅, т.к. αk ⊆S6 и αk ⊆ S3). Среди этих пар нет пары (S5, S6), из чего следует, что частное суждение «некоторые мошенники честные» (S5 ∩ S6 ≠ ∅) не является заключением в данном примере. Тот же результат можно получить, если рассмотреть ветви, исходящие из литерала S6, который в силу ограничения пустоты соответствует непустому множеству.
Предложенный в Примере 2 метод разрешения противоречий можно обосновать и для общего случая, который выражен в следующей теореме.
Теорема (элиминация парадокса с помощью преобразования общего суждения в частное). Если противоречие в рассуждении вызвано цепью включений литералов L 1 ⊆ L 2 ⊆ … ⊆ L n , при условии L n = L 1 , то элиминировать парадокс можно с помощью выбора в этой цепи пары литералов ( L i , L i +1 ) и заменой соотношения L i ⊆ L i +1 двумя соотношениями α k ⊆ L i и α k ⊆ L i +1 при условии α k ≠ ∅ .
Доказательство . При замене в графе включений разрывается путь, ведущий от L 1 к L 1 , т.к. в исходной цепи дуга L i → L i +1 преобразуется в подграф L i ← α k → L i +1 . В цепи, которая образуется из контрапозиций дуг, входящих в исходную цепь, и также, как и исходная, представляет путь из L 1 к L 1 , при замене также происходит разрыв, т.к. дуга L i → Li заменяется на подграф L i → αk ← Li , который препятствует достижению литерала L 1 из литерала L 1 . Тем самым доказывается, что при замене общего суждения L i ⊆ L i +1 частным суждением L i ∩ L i +1 ≠ ∅ парадокс элиминируется. Конец доказательства .
Таким образом, замена хотя бы одного общего суждения в цепи включений, ведущей к парадоксу, частным суждением позволяет устранить противоречие, но в ряде случаев такая логическая ошибка как замена частного суждения общим приводит правильное рассуждение к парадоксу.
Для решения Задачи 6 (распознавание безусловно непустых множеств в системе) используется закон существования (iii). В Примере 2 из условий задачи ясно, что изначально заданными непустыми множествами в системе являются S6 и αk. На графе включений (рисунок 4) можно проследить все ветви, исходящие из этих литералов. По закону существования любой литерал, содержащийся в этих ветвях, соответствует безусловно непустому множеству. Из анализа Примера 2 ясно, что безусловно непустыми множествами являются все, за исключением S3 (трезвенники), т.к. только в этот литерал нет пути из литералов S6 и αk.
5 Недостатки силлогистики
Включение теории категорического силлогизма практически во все учебники логики означает, что данная система логического анализа рекомендована к практическому использованию и по своему назначению не допускает ошибок. Однако эта система обладает рядом недостатков. К ним относятся нестрогое и труднопонимаемое теоретическое обоснование, а также недостаток аналитических средств, что не даёт возможности решать более сложные задачи логического анализа рассуждений, включающих распознавание подмены терминов, парадоксов и формирование абдуктивных заключений. Эта теория в некоторых случаях приводит к ошибочным результатам логического анализа, в частности к тому, что некоторые корректные рассуждения распознаются в ней как неправильные модусы [16].
Заключение
Предложенные методы преодоления заблуждений в современной логике позволяют решить ряд проблем, связанных с рассуждениями и обоснованиями, в которых используются отношение включения множеств и изоморфное ему отношение следования. В основе этих методов лежат законы алгебры множеств, которые можно доказать без использования аксиом с помощью рассмотренных в статье вариантов соотношений между множествами.
В работе усовершенствована математическая модель полисиллогистики, в которой в качестве правил вывода используются законы транзитивности и контрапозиции. В модель рассуждений добавлены ограничения в виде неравенств, что позволяет распознавать ошибки в рассуждении. Предложенные изменения позволили расширить аналитические возможности силлогистики и устранить её недостатки. В качестве объектов модели можно вводить не только простые множества, но и формулы исчисления высказываний и предикатов, выраженные с помощью алгебры кортежей, что позволяет использовать данную модель рассуждений в информационных системах, основанных на знаниях.
Для решения ряда задач логического анализа сформулированы и обоснованы новые законы алгебры множеств: закон парадокса, условие непустого пересечения и закон существования.
Список литературы О заблуждениях в современной логике
- Курант Р., Роббинс Г. Что такое математика? / Пер. с англ. под ред. А.Н. Колмогорова. М.: МЦНМО, 2015. 568 с.
- Мендельсон Э. Введение в математическую логику / Пер. с англ. Ф.А. Кабакова. М.: Наука, 1971. 320 с.
- Mendelson E. Introduction to Mathematical Logic (6th ed.). Boca Raton, London, New York: Taylor & Francis Group, 2015. 499 p.
- Бочаров В.А., Маркин В.И. Введение в логику: учебник. М.: ИФРАН, 2008. 560 с.
- Гетманова А.Д. Учебник логики. Со сборником задач. М.: КНОРУС, 2011. 368 с.
- Томова Н.Е., Шалак В.И. Введение в логику для философов. М.: ИФРАН, 2014. 191 с.
- Ивлев Ю.В. Логика: учебник. 4-е изд. М.: Проспект, 2022. 304 с.
- Copi I.M., Cohen C., McMahon K. Introduction to Logic. New York: Routledge, 2016. 654 p.
- Бурбаки Н. Теория множеств. М.: Мир. 1965. 455 с.
- Френкель А.А., Бар-Хиллел И. Основания теории множеств. Перевод с англ. Ю.А. Гастева. М: URSS. 2010. 556 с.
- Halmos P. Naive Set Theory. New York: D. Van Nostrand Company, 1960. 111 p.
- Мальцев А.И. Алгебраические системы. М.: Наука, 1970. 392 с.
- Сазонов В.В. Алгебра множеств // Математическая энциклопедия. М.: Советская энциклопедия. Т.1. 1977. С.129-130.
- Секей Г. Парадоксы в теории вероятностей и математической статистике / Пер. с англ. В.В. Ульянова под ред. В.В. Сазонова. М.: Мир, 1990. 240 с.
- Столл Р.Р. Множества. Логика. Аксиоматические теории / Пер. с англ. Ю.А. Гастева и И.Х. Шмаина. М.: «Просвещение», 1968. 231 с.
- Кулик Б.А. Почему в учебниках логики содержатся логические ошибки? Образовательные ресурсы и технологии. 2023. № 1(42). С.7–14. DOI: 10.21777/2500-2112-2023-1-7-14.
- Кулик Б.А. Логика и математика: просто о сложных методах логического анализа. СПб.: Политехника, 2020. 144 с.
- Кэрролл Л. Символическая логика / Пер. с англ. Ю.А. Данилова // Кэррол Л. История с узелками. М.: Мир, 1985. С.189-362.


