О задаче гашения поперечных колебаний продольно движущейся струны

Особенностью задач гашения колебаний гиперболических систем является то, что в них оптимальный режим зависит не только от времени, но и от пространственных переменных. Поэтому для нахождения минимального времени гашения колебаний и соответствующего ему оптимального уравнения используется метод сведения этой задачи к т. н. тригонометрической проблеме моментов. Наиболее значимой работой в этом направлении является статья Дж. Лагнеса [1], где, в частности, исследована возможность гашения колебаний закрепленной струны:

2 W a

^- w xx + q ⁽ x ) ^w = g ⁽ x,¹ ) ,

v < x < l, t > 0,

"'■=o = hо (x), "' ■=o = h (x), 0 < x < l,

4=0=4=l=0, t >0, где начальные данные h0(x) и h 1(x) - начальные возмущения, g(x, t) – функция управления; при этом предполагается, что потенциал q(x) – непрерывная неотрицательная функция на отрезке [0, l]. Решение смешанной задачи рассмотрено как обобщенное [2], для которого определен интеграл энергии:

l

E ( t ) = / [ w ( x ’ t )⁺ a 2 ( w 2 ( x ’ t )⁺ q ( x ) w ² ( x ’ ¹ ) ) ] dx ’

который при g ( x, t ) = 0 не зависит от t и равен значению E (0). Задача управления системой (1)‒(3) заключается в возможности ее перевода из начального состояния (2) в произвольное:

¹¹'.= T = Ко ( ^x ) , ^ J , = _T = К ( x ) , x ^G [ ^0, l ] , ⁽⁵⁾

где h 0 И 0 e W 1 ( 0, l ) , h , \ e L 2 ( 0, l ) и T >  0 за счет выбора управляющей функции g ( x , t ) e L ₂. Вслед за Ж. Лионсом [3] ученые называют такую ситуацию строгой управляемостью.

Задача гашения колебаний заключается в нахождении минимального значения T 0 > 0, при котором для любых начальных возмущений h 0 е W 11 ( 0, l ) , h 1 е L ₂ ( 0, l ) найдется управляющая функция g 0 ( x , t ) e L 2 ( 0 <  x <  l , 0 <  t <  T₀ ) (определяющая оптимальный режим) такая, что

E ( T o ) = 0,               (6)

или, говоря другими словами, при g ( x, t ) = g ₀ ( x, t ) решение задачи (1)-(3) при T = T₀ принимает вид:

w|    = 0, w = 0 .         (7)

1 = T₀        , t t = 0

Из закона сохранения энергии (4) следует, что решение граничной задачи при (1), (3) и g ( x , t ) = 0 представляет собой т. н. «стоячие волны», которые можно найти методом разделения переменных, или методом Фурье. Они представляются в виде:

z n ( x , t ) = ⁽ A n ^cos ® n t + B n ^sin ® n t)v n ( x ) , ⁽⁸⁾

где v_n ( x ) (решения соответствующей спектральной задачи)

-v"(x) + q (x) v (x) = Xv (x), 0 < x < 1, v (0) = v (l ) = 0          (9)

образуют ортонормированный базис в L 2 ( 0, l ) и являются собственными функциями задачи (9), отвечающими собственным значениям X _n , n = 1,2, ^ При этом 0 < Х 1 < Х ₂ <^< Х _п < ^ образуют монотонно возрастающую последовательность, и для них справедливо асимптотическое разложение:

Гл aⁿⁿ , 1 ]

to n = a JXn = —— + c_n + O I - I , n ^w . (10) l V n )

Выполнение условий (7) для построенной методом разделения переменных смешанной задачи (1)-(3) приводит к системе интегральных уравнений Фредгольма первого рода:

[ V ( t ) cos tontdt = -p n ,

^J T                      n = 1,2, ^ , (11)

J ^un (t) sin totdt = anrnn, которую принято называть тригонометрической проблемой моментов. Здесь an, Pn, un (t) _ коэффициенты разложения функций h0 (x), h( x) и g (x, t) по ортонормированному базису {vn (x)}.

Таким образом, решение задачи гашения колебаний сведено к нахождению минимального значения времени T ₀ разрешимости бесконечной системы (11), т. е. существования решения u 0 ( t ) , ^ , и П0 ( t ) этой системы в пространстве L 2 ( 0, T ) , для которого справедлива оценка:

а

X u⁰ ( t ) ^ 2 ( V , l ) <  const ( ^h o W 1 ( 0,1 ) ⁺ h L 2 ( 0, l ) ) ^ j = ⁰

< const E ( 0 ) .            (12)

Заметим, что из (10) вытекает существование предела lim n= l.(13)

n → N ω _n απ

Поэтому, согласно результатам, полученным Н. Левинсоном [4], при l T2

— = ——, т. е. при Т0 = — система {cosront, sin ront} образует базис Рисса в L2 (0, T0). Следовательно, для нее существует биортогональная система в L2 (0, T0), что позволяет установить существование единственного решения {и{0) (t)} системы (11), а также найти оптимальное управление g0 (x, t) в виде ряда продольно движущейся струны, возникающей в производстве бумажного полотна. Исследования поперечных колебаний продольно движущейся струны начались около 60 лет назад [2; 5–6]). Была предложена следующая модель поперечных колебаний w (x, t), связанных с движением бумажного полотна (см. рисунок) [7].

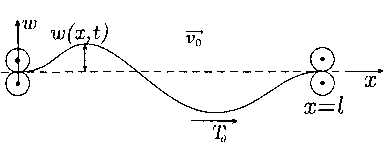
Р и с у н о к. Форма движущегося бумажного полотна

F i g u r e. Shape of moving paper web

w g0 (x, t^^un, (tX (x).     (15)

n = 1

Отметим, что результаты, полученные Дж. Лагнесом [1], имеют важное значение, поскольку из них вытекает гарантированное время гашения колебаний. Показано, что управляющую функцию можно использовать и в любой подобласти [ c , d ] отрезка [0, l ], который на практике может иметь достаточно большую длину l . Однако приближенное оптимальное управление построить весьма затруднительно, т. к. приходится решать бесконечную систему интегральных уравнений для сопряженных функций и суммировать бесконечный ряд (15) в ситуации, когда его оценка стремится к бесконечности для ( d - c ) ^ 0.

Поэтому все дальнейшие работы для (приближенного) решения задачи гашения колебаний, обзор которых будет сделан ниже, основаны на существенном сужении класса управляющих функций, причем в них рассматриваются не только струны, но и мембраны, балки и пластины.

Целью работы является решение задачи гашения поперечных колебаний

Physics and mathematics

Здесь _ г ₀ - вектор продольной скорости, Т₀ - вектор продольной силы на единицу длины, m ‒ масса единицы длины:

Id w _ d w 2 m      + 2 v_n---- + v_n

I d t ²       0 d x d t    0

d ² w d x ²

—

T ^ w = 0 .

⁰ d x ²

Поэтому, приняв

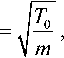
можно

привести данное уравнение к виду:

d2w dt2 + 2 v0

5 ² w

+ 5 x 5 t

v o2 ^- c

d 2 w dx ²

0 <  x <  l , t >  0.

При этом заданы граничные условия

w ( 0, t ) = w ( l , t ) = 0, t >  0 (17)

и начальные возмущения:

w ( x, 0 ) = h о ( x ) , W t ( x, 0 ) = h ( x ) , x e [ 0; l ] .                 (18)

Для решения смешанной задачи справедлив аналогичный случаю закрепленной струны закон сохранения энергии:

l

E ( t ) = j [ w 2 ( x, t ) + ( c 2 — v 0 ) w 2 ( x, t ) ] dx - E ( 0 ) =

l

= J [ h ( x ) + ( c ^{2 -} v 0 ) (h о ( x ) )² ] dx . (19)

Таким образом, кориолисово ускорение 2 v ₀ w_xt не вносит вклад в энергию системы, и в ней должно существовать решение в виде стоячих волн. Но из-за наличия члена 2 v ₀ w_xt их невозможно найти традиционным методом разделе-

ния переменных.

Тем не менее данные функции най-

дены с использованием специальных

функций и образуют систему решений

I , ikn 2      2              I vk (x, t) = exp j ±——1_ v0 — c J t — v0 x ^, k = 1,2,™

—

В работах Л. А. Муравья и Б. Т Билалова1-2 [8] при естественном пред-

условий оптимизации градиентного спуска.

Обзор литературы

Как уже было отмечено, исследования, посвященные гашению колебаний упругих систем, различаются как управляемыми объектами, так и классами управляющих функций, часто называемыми демпферами.

Начнем обзор с работ, посвященных задаче гашения колебаний струны. В 1978 г. Дж. Расселл [4] предложил использовать только одну управляющую функцию (т. н. распределенный демпфер):

g ( x, t ) = u ( t ) f ( x ) , 0 <  x <  l, t >  0, (20) где f ( x ) - некоторая заданная функция. Тогда проблему моментов (11) при ( q ( x ) = 0 ) можно записать в виде:

положении v ₀ <  c показано, что система { v k ( x , 0 )} образует базис Рисса в L 2 ( - l, l ) . Это позволяет построить обобщенное решение смешанной задачи (16)‒(18) с управляющей функцией g ( x, t ) е L ₂(0 <  x <  l , 0 <  t <  T ) .

Доказано, что при тригонометрическая

lc

T0   2 12

n ( c - v 0 ) проблема мо-

T ncmt i                    nan

I e l u ( t ) dt = - P _n + 1 ——« „ , 0

n = 1,2, ™ ,            (21)

где

. ^f n = ^2 J. f ( x ) sin ^ Ondx

ментов, вытекающая из условия E ( T₀ ) = 0, имеет единственное решение: { u ° ( t ) , ™ , u k ( t ) , ™ } в L 2 [ 0, T₀ ] .

Исследованы различные классы управляющих функций для построения приближенного решения, которые позволяют установить необходимые условия оптимальности или получить численное решение задачи гашения колебаний, используя методы

должны быть ≠ 0.

Видно, что при T ₀ = — система экс

понент 1

ann i elt

a образует ортогональ-

ный базис в комплексном пространстве L 2 ( 0, T₀ ) , и функция оптимального управления u ₀ ( t ) представляется в виде:

• ¹    Muravey L. A. On the suppression on membrane oscillations // Dynamical Problems of RigidElastic System : Summaries of IUTAM Symposium. Moscow, 1990. P. 50–51.

• ²    Билалов Б. Т., Муравей Л. А. О гашении колебаний больших механических систем // Интеллектуальные системы : тр. 2-го междунар. симпоз. «Интелс-96». М. : РУДН, 1996. С. 246–254. 476 Физико-математические науки

го    nant u0 ( t ) = ReTe ' 1

n = 1

- P n

. nan 1

+ i       I ^a n

„ l ^V . (23)

f n

Заметим, что, если f ( x ) e L 2 ( 0, l ) , то в силу равенства Парсеваля f_n ^ 0, n →∞. Значит, ряд (23) не сходится в L 2 ( 0, T 0 ) , и, таким образом, оптимальное решение w ( x , t ) задачи (1)-(9) при f n ^ 0, n ^ го не принадлежит энергетическому пространству (для него не определен интеграл энергии).

Если принять / „ = 1 , то получим, что:

ность оптимального уравнения u ₀( t ) пространству L ₂(0, T ₀) требует значительной гладкости начальных возмущений h ₀( x ) и h 1 ( x ).

Основными в работах авторов являются т. н. «точечные движущиеся демп-феры»3, а именно уравнения вида:

g ( x, t ) = u ( t ) 5 ( x - x ₀ - 5 ( t )) . (26)

2     . nnx _е .

•f (x) = тЕsin / = 5(x), (24) l n=1          l где 5 (x)- дельта функции Дирака. Далее приходим к исследованию проблемы моментов для управлений вида:

g ( x, t ) = u ( t ) 5 ( x - x 0 ) , x 0 e ( 0, l ) (25)

t

Здесь x ₀ e ( 0, l ) , а s ( t ) = jv ( t ' ) dt ', где v ( t ) - функция ограниченной вариации на отрезке [0, T ]. Таким образом, имеем две управляющие функции u ( t ) e L 2 ( 0, T ) и v ( t ) е V [ 0, T ] (т. е. для любого разбиения 0 <  1 0 <  t 1 <^< t n = T отрезка [ 0, T ] ^ ^ ( L ) ^-v ( t j - 1 )| <  const ).

j = 1

Заметим, что введение точечных движущихся демпферов вполне естест-

(т. н. неподвижные точечные демпферы).

Исследованию проблемы момен-

тов для случая неподвижных точечных демпферов посвящен ряд работ А. Г. Бутковского [10]. Из них, в част- Г fП П )

ности, следует, что для fn = sin I — x0 I точки x0 = —, k, n = 1,2,_, k < n обра-nl

венно, поскольку множество точек неуправляемости системы имеет лебе-говскую меру нуль на [0, T ], а значит, введение второй управляющей функции v ( t ) позволяет почти всем t e [ 0, T ] находиться в точках управляемости, и тем самым избежать появления неже-

лательных стоячих волн.

Проблема моментов для простейшего демпфера вида (26), а именно

x ₀ = 0 и 5 ( t ) = bt , 0 <  t

зуют множество точек неуправляемости системы (1)-(3). В этом случае возникают решения соответствующей однородной системы в виде стоячих волн типа (8), энергия которых постоян-

и s

⁽ t ⁾⁼ » ^- t •

l 2 1

b ^t b ,

на и отлична от нуля, причем множество точек неуправляемости плотно на всем отрезке [0, l ]. Это затрудняет построение устойчивых алгоритмов численного (приближенного) решения задачи гашения колебаний в точках управляемости системы. При этом принадлеж-

где b = const >  a , исследована Б. Т. Билаловым и соавторами⁴ [7]. В частности, было показано, что возникающие в случае простейшего демпфера тригонометрические системы

ei

n ant

l sin

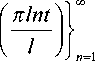
• ³    Muravey L. A. On the suppression on membrane oscillations // Dynamical Problems of RigidElastic System : Summaries of IUTAM Symposium. Moscow, 1990. P. 50–51.

• ⁴    Там же.

^.

образуют базис Рисса в L₇ ( 0, T ) , где 2 l ²

T = —. Значит, время гашения колебаний точечным движущимся демпфером меньше времени гашения колебаний, полученного Дж. Лагнесом.

Использование точечного движущегося демпфера (26) при ограничениях a <  c <  x ₀ + 5 ( t ) < d <  b позволило разработать эффективные численные методы гашения колебаний струн, круглых и прямоугольных мембран [11–13], а также балок и прямоугольных пластин⁵ [14]. Более подробный обзор результатов по этой теме содержится в монографии авторов статьи [15].

Ряд работ В. И. Ильина и В. М. Моисеева [16–18] посвящен граничному уравнению колебаний струны.

Материалы и методы

Построение обобщенного решения задачи поперечных колебаний продольно движущейся струны

Сначала рассмотрим уравнение (16) для всех x е ( -да , + да ) и t > 0. При естественном ограничении c >  v ₀ решение x = ф ( t ) уравнения характеристик для (16) имеет вид:

( ф ')² - 2 v о ^+ v 02 - c ² = 0 , ⁽²⁸⁾ откуда следует, что ^ '( t ) = v ₀ ± c , и характеристики уравнения (16) имеют вид:

^ = x - ( v ₀ + c ) t , п = x + ( c - v ₀ ) t . (29)

Общее решение уравнения (1) имеет вид:

w ( x, t ) = f ( x-(v 0 + c ) t ) + g ( x + ( c - v0 ) t ) , (30)

где f , g – произвольные функции из C² , ( 0 <  x <+® , t >  0 ) .

Том 28, № 4. 2018

Следует отметить, что представление (30) позволяет решить задачу Коши и особенно эффективно при численных решениях смешанной задачи (1)-(3) методом характеристик.

Для решения w ( x , t ) смешанной задачи (16)-(18) обычным приемом [13] устанавливается закон сохранения энергии:

l

E ( t ) = J [ w 2 t ( x , t ) + ( c 2 - ^v o ) w 2 x ( x , t ) ] dx = E ( 0 ) = o

l

= J[h (x) + (c2 - vо )(hо (x))2]dx, (31) о поэтому естественно искать решения смешанной задачи из соответствующего энергетического пространства [13]. При этом для вывода проблемы моментов требуется найти его решение в виде ряда стоячих волн. Заметим, что исследованию стоячих волн задачи (1)–(2) посвящено достаточно большое количество работ, в частности, Н. В. Бани-чука и соавторами [7]. Кроме того, целый ряд исследований (например, [19]) посвящен изучению стоячих волн приближенного уравнения (16).

Для вывода проблемы моментов необходимо найти такую систему стоячих волн v k ( x, t ) , k = 1,2, ^ , чтобы система { v_k ( x ,0 )} ” _ч была базисом Рисса в L ₂ ( - 1 , l ) . Для этого сначала нужно найти комплексные решения задачи (16)–(17):

v ( x , t ) = exp { ± i a ( v 02 - c ² ) p t - v ₀ y x } sin ( a x ) .

Непосредственно проверяется, что уравнение (16) выполняется при α > 0

и Y = в = , а граничные условия (2) - c kn при a = ak = —, k = 1,2,^

Таким образом, мы получим систему функций

Y = в = 1 , c

задающих все решения задачи (10), (15). Из (33) при t = 0 выведем систему

. v 0 ( k n x ^         ,      \

± i I I

V k ( x ) = e c I l ^ sin I —1 , k = 1,2, ^ , (34)

которая исследована в работах Б. Т. Билалова и Л. А. Муравья6 [8]. Отсюда, в частности, следует, что при v0 < c эта система в виде to

Ea2 < consthо (x)42(0,l), k=1

to

ZX < consth(x)\(о,i), k=1

to

E a^{2 k 2}< ^consth0) ( x ) 4 ( - 1 , i ) . k = 1

Теперь введем функцию управления g ( x , t ) e £ ( П_т ) , где П_т = { 0 <  x <  l , 0 <  t <  T } ; представим решение смешанной задачи для уравнения:

^W + ² v 0 w x + ( v 02 - c 2 ) w x = g ( x , t ) ,

{ У к ( ^x ) , z k ( x ) } =

0 <  x <  l , 0 <  t <  T

(knv  V knx  . (knvn  1 . knx cos 0x sin ,sin 0x sin

I 1c   J 1 I 1c   J I образует базис Рисса в пространстве L2 (-1, l).

Следовательно, решение w0(x, t) смешанной задачи (16)-(18) из энергетического пространства определяется единственным образом в виде ряда с граничными условиями (17) и начальными условиями (18) в виде w = w0 + wg, где

t wg (x, t) = JW(x, t -т, т)dT, (39)

где w(x, t - т, т) является решением смешанной задачи при начальных условиях to wo (x, t )=E k=1

^а к У к ( x ) ^cos

k

^{k n} ( ^{c 2 - v} 02 ) lc

) t

+

AV 1 1 = T = 0, AV 1 1 = T = g ( x , T ) .      (40)

+ P k

clz_k ( x )    . ^{k n} ( c ^{2 - v} 02 )

k        sint kn ( c2 - v02) lc

Таким образом,

, (36)

,    4 ” zk (x) cl w. (x, t )=x t; 2   21x k=1 kn (c - v0 )

где a_k - коэффициенты Фурье продолженной нечетным образом на [- l , 0] функции h ₀ ( x ) е W 1 ( 0, l ) ; в_к — коэффициенты Фурье продолженной четным образом на (- 1 , 0) функции h 1 ( x ) е L 2 ( 0, l ) по системе [ y_k ( x ) , z_k ( x ) ], биортогональной рассматриваемой системе { Z k ( x ) , n_k ( x )} • При этом справедливы оценки

t x^uk (t ) sin

kn(c - v0) — lc

V

)

( t - t ) d T , (41)

J где uk – коэффициенты разложения функции g(x, t), продолженной четно по x на отрезок [-l, 0], по системе {zk(x)}.

Результаты исследования

Решение задачи гашения поперечных колебаний продольно движущейся струны заключается в нахождении такого минимального значения времени t = T 0 , при котором для любых допустимых начальных возмущений h 0 ( x ) е W 0 ( 0, l ) , h 1 ( x ) e L 2 ( 0, l ) найдется такое оптимальное управление g ₀ ( x , t ) e L 2 ( 0 <  x <  l , 0 <  t <  T₀ ) , что в момент времени t = T ₀ для решения w ( x , t ) = w ₀ ( x , t ) + w_g ( x , t ) смешанной задачи выполняются равенства

W ( x , T o ) = 0, W ( x , T o ) = 0, x ^G [ 0, l ] , ⁽⁴²⁾

т. е. энергия системы в момент времени t = T ₀ обращается в 0. Из представлений (36), (41) с помощью стандартных преобразований находим следующую систему интегральных уравнений первого рода:

lim A = _Jc -- .     (45)

k ^” ^ n (c ² - V a ^:) k 0

Таким образом, из результатов

• Н.    Левинсона [4] следует, что система lc T

• (44)    при —------- - = —0 , т. е. при

п ( c — v о ) ^{2 п}

To = T^lc-2 ,        (46)

( ^{c -} v o )

образует базис Рисса на отрезке [0, T 0 ]. Следовательно, для нее в L ₂(0, T ₀) существует биортогональная система { Ф к ⁽ t ) , V k ⁽ t ) }• А значит, существует решение проблемы моментов:

uk (t) = Pk9k (t)- ам.у (t), t e[0, To], к = 1,2,^       (47)

T

U ( t ) cos 0

^{z k n ( c 2 -}

1c k

-2 ) )

⁰¹1 dt = - P k ,

T j u_k ( t ) sin ⁰

^{k n} ( ^c 2 ^{- v} o2 )

1c

k

^

t

kn ( c ² - dt = a_k —----

v 0 ²

k = 1,2,_,             (43)

называемую проблемой моментов относительно тригонометрической системы

Таким образом, вызываемые начальными возмущениями h0(x) и h 1(x) колебания w(x, t) можно погасить за минимальное время T0, не зависящее от h0(x) и h 1(x), для всех допустимых возмущений. При этом оптимальное управление g0(x, t) представляется в виде сходящегося в L2 (ПТо) ряда го gо (x, t) = Tu° (t) zk (x)     (48)

k = 1

^ cos

^{k n} ( c ^- v 0 )

Tc

V

^ t

/

,sin

^{k n} ( ^{c -} v 0 )

Tc

V

' 1; ■

k = 0,1, _           (44)

на отрезке [0, T ]. Приняв ю_к = получим, что

kn ( c ² - v 00 ) lc

и удовлетворяет оценке g0 (x, t)2,(To) ^ const(ho (x)L2(0,l) + (hh (x)L2(0,l))•

Следует отметить, что найденное

T ₀ должно удовлетворять неравенству

T 0 и ₀<  l , которое выполняется при дополнительном ограничении на и ₀

и 0 < ( V2 - 1 ) c .         (50)

О классах управляющих функций

Заметим, что в случае и ₀ = 0 время гашения колебаний совпадает со временем гашения колебаний закрепленной струны, установленным Дж. Лаг-несом [1]. Исследователь показал, что за это же время можно погасить колебания струны, если управление g ( x , t ) сосредоточено на произвольном отрезке [ у , 5 ] с [ 0, l ] , т. е. при g ( x , t ) g L 2 ^ у <  x <  5 ,0 <  t <  T о ^, где ' 2 1

Tо = . Аналогичный результат спра-c ведлив и в рассматриваемом случае. Действительно, если g (x, t)e L2 (Пт) и supxg (x, t )G[ Y, 5], то вместо проблемы моментов (43) получим проблему моментов

^T o 5

jj g ₀ ( x , t ) cosa>_ntdxdt = - Д ,,

<

;;                         n = 1,2, ^ (51)

T o 5

jj g o ( x , t ) sinto„tdxdt = a_n to „ ,

. 0 у

В этом случае искомое решение g ₀( x , t ) системы (51) имеет вид:

to g о (x, t)=Z(42®„a„y„ (x M (t)- Bn Pnzn (x ))• n=1

X [ a, в ]( x ) ’ где X[Y,s] (x) - характеристическая функция отрезка [у, 8],

(5        У1      (8У

A n = y x ( ( x ) dx   , B n = z² ( ( x ) dx ,

IY         J         IYJ n = 1,2,^

При этом /и/^2 > const (5 - у) и, аналогично, infBn > const (8 - у).

Следовательно, построенное оптимальное управление g0(x, t) удовлетворяет оценке g о (x, t )L 2

_< const

8 - y

(hn (x)2Z A+ h,(x)2.

⁰         L 2 ( 0, l )         ¹         L 2 ( 0, l )

В данной статье будем предполагать, что управляющая функция g ( x , t ) имеет вид:

k = 1

где 0 <  x 1 <^< x k <  l , а x k ( x ) — характеристическая функция на отрезке [ x k - e , x k + e ], при этом e > 0 достаточно мало, так что все указанные отрезки не пересекаются и принадлежат отрезку [0, l ]. Дополнительная информация представлена в работах А. Макмудова и Л. А. Муравья⁷ [20].

Введем минимизируемый функционал:

l

J ( t ) = E ( t ) + X J g ² ( x, t ) dx =

l

= J [ w 2 ( x, t ) + ( c ² — v 0 ) w X ( x, t ) ] dx +

K

+ 2 Xs ^ u 2 ( t ) .             (57)

k = 1

Примем 2 Xe = ц и будем считать функции u_k ( t ) кусочно-постоянными:

uk ⁽ t ) = u kp , при t p -i < t < t p , P = 1, ^2, ... ^{, P (58)}

Здесь P может принимать значения от 1 до N, где N - число шагов по вре- мени, используемых при численном решении задачи.

Таким образом, функционал J становится функцией значений u_kp , и для применения градиентного метода требуется значение всех частных произ-

5J —  — водных----, к = 1, K, p = 1, P. d и,п xp

Обсуждение и заключение

В статье получено обобщенное решение уравнения движения бумажного полотна; с помощью стандартного приема установлен закон сохранения энергии колебаний. Показано, что возникающая система собственных функций I   (knv V knx . kknv V knx I cos 0x sin     ,sin 0x sin

[    ( Ic ) l ( Ic ) l образует базис Рисса в соответствую-

Том 28, № 4. 2018

щем функциональном пространстве, что позволило установить минимальное время гашения колебаний и явно выписать управляющую функцию, которая гасит эти колебания. Также описан класс управляющих функций; показана возможность применения градиентного метода для поиска минимума функционала энергии. Такой метод численной оптимизации будет рассмотрен в дальнейших работах, где будут также установлены необходимые условия оптимальности в форме принципа максимума Л. С. Понтрягина (аналогично тому, как это сделано в статье А. А. Гурченкова и соавторами [21]) и приведены графические иллюстрации оптимальных режимов и процесса гашения колебаний.

Поступила 19.06.2018; принята к публикации 15.08.2018; опубликована онлайн 28.12.2018

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.