О задаче идентификации начального гидродинамического участка при ламинарном течении ньютоновской жидкости в горизонтальном кольцевом канале

Кольцевая геометрия, наряду с цилиндрическими трубами и плоскими каналами, наиболее часто используется в различных технических системах [1]. В [2] показано, что проведение про- цесса теплопередачи в режиме начального гидродинамического участка является одним из способов интенсификации теплообмена. Поэтому выявление закономерностей формирования структуры поля скоростей на начальном участке и определение его длины в направлении течения жид- кости актуально.

Впервые такая задача для кольцевого канала была рассмотрена в [3] на основе погранслойно-го приближения с применением линеаризации Лангхаара [4]. Детальный обзор последующих теоретических и экспериментальных исследований этой проблемы [5] показал, что различие в определении характеристик начального гидродинамического участка существенно. Уточнение длины начального гидродинамического участка на основе численного интегрирования уравнений Навье–Стокса, например [6], вызывает вопросы корректности используемых вычислительных процедур, связанных с существованием и единственностью решения самих уравнений. Предпринимаются также дальнейшие попытки отыскания аналитических решений, например, использующих идеализацию о «ползущем» течении [7].

В связи с этим в данной работе с позиций физической линеаризации уравнения пограничного слоя на основе гипотезы однонаправленности течения формулируется и аналитически анализи- руется задача отыскания длины начального гидродинамического участка в горизонтальном кольцевом канале.

Постановка задачи. Математическая формулировка задачи в цилиндрической системе координат имеет вид [8]:

(ди ди ди р|    +u-^r+U

к д t д r дz

д + п д r

2 д ( д и ^ 2 u д ( д и ди

I - ^r- I -r - +I z + r r д r к д r J r ²    д z к д r     д z

f ди   ди   ди

P l    ⁺ U. z ^{+ u} z^

к д t       д r       дz

д p     I 1 д

— + п 1— д z I r д r

f ди ди ) r l + ^ r I к д r д z J

+ 2 " ^U 1 ;

д z ² J’

1 д , ч ди т (rur)+=0; r д r        дz ur (r, z ,0) = uz (r, z ,0) = 0, ur (r ,0, t ) = 0, uz (r ,0, t ) = u0 = const;

ди (r,l,t) ди (r,l,t) A / x /                                    / x a

—4;-----= —z—-----= 0, Ur (r1, z, t ) = uz (r1, z, t ) = 0, ur (r2, z, t ) = uz (r2, z, t ) = 0, дz          дz

где u r , u _z - радиальная и аксиальная компоненты вектора скорости жидкости; p - избыточное давление; р , п - плотность и коэффициент динамической вязкости жидкости; t - время; r 1 , r₂ -радиусы внутренней и внешней соосных цилиндрических труб, составляющих кольцевой канал; l - длина кольцевого канала ( l » r₂ ) .

О задаче идентификации начального гидродинамического участка при ламинарном течении ньютоновской жидкости в горизонтальном…

Как правило, для замыкания системы (1)–(5) дополнительно рассматривается уравнение относительно давления [9]

1 д ( д p )  д ² p       ( 1 д (   ди )   1 д Г  д ( r u )

д ( ди 1 д ( ди М

+ — I V r --“ I + I V z --“ If + д z к   д r J д z к   д z J ]

fди  ди J11

r z + r . к д r    д z JJ]

--1 r— I + —у = - р i 1 r v_r —- | + vz ——— r д r к д r J  д z ²        I r д r V    д r J   r д r L д z

1 д2 f диJ д3и 1 д fVJ 1 д2 --ТI r—r" I ++—z 1 I + r д r2 к д r J дz3 r д r к r J r д r дz с краевыми условиями p (r ,0, t ) = p о = const, дp(r, l, t) = 0,(7)

д z дp (r1,z, t) = дp (r2,z, t) = 0(8)

д r        д r "°

Пусть течение по всей длине канала является однонаправленным, т. е. v _r = 0, тогда из (3)

следует, что V _z = V _z ( r , t ) , причем (1) вырождается в д p/ д r = 0, а (2) трансформируется в

с граничными условиями ди   дp П д ( ди J P—z = ——+ — — r—z                     (9) ■ д t д z r д r к д r J Vz (r ,0 ) = V0, Vz (T1, t ) = Vz (r2, t ) = 0                                 (10) и выполнением балансового соотношения

2     r 2 2 2 J r V z ( r , t ) dr = V 0 .                                       (11) r 2 - r 1 r 1

При этом из (6) следует постоянство аксиального градиента давления, т. е. дp/д z = const.

В безразмерном виде система (9)–(11) запишется

^V = - + -LI A f R » J ;                     (12) дZ     ReR дR к дR J V(R,0) = 1; V(R1,Z) = V(R2,Z) = 0;                          (13) R2 2     JRV (R, Z)dR=1,                             (14) R 2 R1 R где T = V0t^d = z/d = Z ; R = r/d ; V = vz/v0 ; P = p](pv0); R12 = r12]d ; Re = v0dpП — число

Рейнольдса; d = 2 ( r ₂ - r 1 ) - гидравлический диаметр; — = - dP/dZ .

Решение. Применим к (12), (13) одностороннее интегральное преобразование Лапласа по переменной Z [10]:

---L- +-- L - sReV_r +1 - + 1 | Re = 0;

dR ² R dR ^L J s J

V_L ( R 1 , s ) = V_L ( R 2 , s ) = 0,                                   (16)

где s , V_L – изображение Z и V соответственно. Решение (15), (16) есть

V_L ( R , s ) = ( - + s )/ s ² + ^ ( R , s )/ ^ ( s ) ,                      (17)

где                    ^ ( R , s ) = ( — + s ) { L K ₀ ( R 1 V sRe ) - K ₀ ( R ₂ V sRe ) J 1 ₀ ( Ry/sRe ) +

+L 1 ₀ ( R ₂ '/sRe ) - 1 ₀ ( R 1 '/sRe ) J K ₀ ( R'/sRe ) } ;

y ( s ) = s² y ( s ) , y ( s ) = 1 ₀ ( R 1 V sRe ) K ₀ ( R ₂ V sRe ) - 1 ₀ ( R ₂ V sRe ) K ₀ ( R 1 V sRe ) ,

I ₀ , K ₀ – функции Бесселя и Макдональда мнимого аргумента [11]. Оригинал первого слагаемого правой части (17) равен [12]

L ¹ [ ( C + s )/ s ² ] = CZ + 1, (18) где L ¹ - обратный оператор преобразования Лапласа.

Для нахождения оригинала второго слагаемого правой части (17) применим вторую теорему Ващенко-Захарченко [13]. Корни знаменателя ^Vs ) = 0 таковы: 1) s = 0 - кратности два; 2) бесконечное счетное множество однократных корней s n уравнения / ( s n ) = 0. Для корня s = 0

* R 0. = lim [ z exp ( sZ ) ^M + exp ( sZ ) J^ - exp ( sZ ) P Ri MT. V ‘ ( 0 ) s > 0 [ ^P        y( s )      ^P        y( s )       ^p          / ( s )

Так как 1 0 ⁽ z ) = 1 1 ⁽ z ) и K 0 ⁽ z ) = - K 1 ⁽ z ) , то

J ( R , s ) = [ K ₀ ( R 1 xhRc ) - K ₀ ( R ₂ V R ) ] 1 0 ( R^sRe ) + [ 1 0 ( R ₂ V R ) - 1 0 ( R 1 ^^sRe ) ] K ₀ ( R^sRe ) + + ( C + s ) V Re { [ R ₂ K 1 ( R ₂ xhRe ) - R 1 K 1 ( R 1 VsRe ) ] 1 ₀ ( R^sRe ) +

+[ K ₀ ( R 1 V sRe ) - K ₀ ( R ₂ V sRe ) ] RI 1 ( R^sRe ) + [ R ₂ 1 1 ( R ₂ V sRe ) - R 1 1 1 ( R 1 V sRe ) ] K ₀ ( R^JsRe ) +

+[ 1 ₀ ( R 1 V sRe ) - 1 ₀ ( R ₂ V sRe ) ] RK 1 ( R^^sRё )}/( 2 V s ) ,

Y ( s ) = V Re [ R 1 1 1 ( R 1 V sRe ) K ₀ ( R ₂ V sRe ) - R ₂ 1 ₀ ( R 1 V sRe ) K 1 ( R ₂ V sRe ) -

- R ₂ 1 1 ( R ₂ V sRe ) K ₀ ( R 1 V sRe ) + R 1 1 ₀ ( R ₂ V R ) K 1 ( R 1 JsRe ) ] /( 2 V s ) , тогда

^ 00 ) =- 1 - CZ + 4 cRe [- ( R ² - R 1² ) + ( R 22 - R 1² ) ln ( RR ) /^ln ( ^R 2/ R ) ] •        < ¹⁹ )

Для корней s_n имеем

® ( R , s n )

E V A exp ( ^sn^Z ) ,                                     ⁽²⁰⁾

n = 1 ^ ( s_n )

откуда следует, что физическому смыслу задачи удовлетворяют чисто мнимые корни, поэтому V s_nRe = u n i или s n = - R 2 Ree .

Так как   1 ₀ ( iz ) = J ₀ ( z ) ;   K ₀ ( iz ) = i ^^ N ₀ ( z ) ;   1 1 ( iz ) = iJ 1 ( z ) ;   K 1 ( iz ) = ^ 2 N 1 ( z ) , где J ₀ ( z ) ,

J 1 ( z ) - функции Бесселя первого рода; N ₀ ( z ) , N 1 ⁽ z ) - функции Неймана [14], то

(    „² ^   (    „² ^

J R , - R l I = I C - R l I i _{ [ N 0 ( R 1 R n ) - N 0 ( R 2 R n ) ] J 0 ( R R n ) + [ J 0 ( R 2 R n ) - J 0 ( R_xR_n ) ] N 0 ( R r_w ) } ;(21) k     Re 7 k Re ) 2 ^{LL                      J                                 J         J}

V I^- Sr J = ^{- R} n i 7 ^{[- R} 1 J 1 ( ^R1 R n ) ^N 0 ( ^R 2 R n ) ^{- R} 2 J 0 ( ^R1 R n ) N 1 ( ^R 2 R n ) ⁺ k Re)   Re 4 ^L

+ R 2 J 1 ( R 2 R n ) N 0 ( R 1 R n ) + R 1 J 0 ( R 2 R n ) N 1 ( R 1 R n ) ] .

Суммируя (18)–(20), с учетом (21) и (22), получим

V ( R , Z ) = 4 CRe - ( R

.² _ R 2 )₊ 1^ R 4 ln ² R 1

R ln

R 1

^

- 2 E ( CRe - R 2 ) { [ N 0 ( R r ) - N 0 ( R 2 R n ) ] J 0 ( R R n ) + n = 1

⁺[ ^J 0 ( ^R 2 R n ) ^{- J} 0 ( ^R 1 R n ) ] ^N 0 ( ^R R n ) } exp k^- ReZ ) I

I { R n [- R 1 J 1 ( R 1 R n ) N 0 ( R 2 R n ) - R 2 J 0 ( R 1 R n ) N 1 ( R 2 R n ) + + R 2 J 1 ( R 2 R n ) N 0 ( R 1 R n ) + R 1 J 0 ( R 2 R n ) N 1 ( R 1 R n ) ] } ,

где R _n - корни уравнения

О задаче идентификации начального гидродинамического участка при ламинарном течении ньютоновской жидкости в горизонтальном… J 0 ( R 1 M n ) N 0 ( R 2 A n ) - J 0 ( R 2 A n ) N 0 ( R 1 A n ) = 0,

R i = 2 R /^{( 1} - R ) , R 2 = 2 /^{( 1} - R ) , R = r i r 2²

; константа С определена из (14) при Z ^ ^

C = Re (1 - R ) 2 Д1 + R + ( 1 - R ²)/ ln R ] ,

совпадающая с результатом в [15].

Анализ. Характерная структура гидродинамического поля безразмерных скоростей на входном участке (рис. 1) показывает, что при малых значениях R наблюдается ассиметрия профиля максимальным значением в сторону поверхности соосного цилиндра скорости со сдвинутым

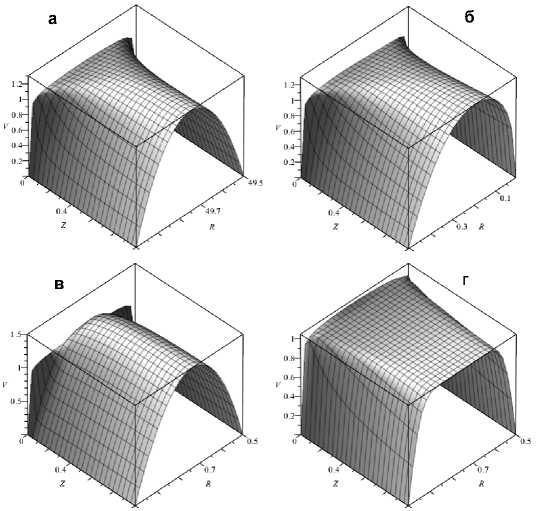
Рис. 1. Поля скоростей, примыкающих ко входному сечению кольцевого канала при различных числах Re и отношениях радиусов внутренней и внешней соосных цилиндрических труб R : а ) Re = 100, R = 0,99 ; б ) Re = 100, R = 0,01 ;

в ) Re = 10, R = 0,5 ; Re = 1000, R = 0,5 ; г ) Re = 1000, R = 0,5

меньшего радиуса, а увеличение числа Re практически линейно увеличивает длину гидродинамического начального участка.

Предполагая, что дрейфом радиальной координаты мак- f (R)

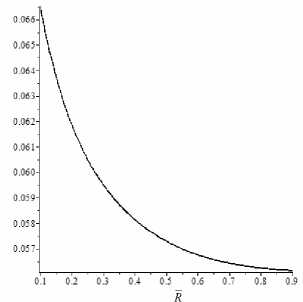
Рис. 2. Вид функции f ( R )

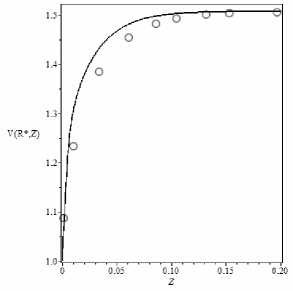
Рис. 3. Изменение максимальной безразмерной скорости вдоль кольцевого канала при Re = 1: ‒ – расчет; ○ – эксперимент

симальной скорости на начальном гидродинамическом участке можно пренебречь и считать ее постоянной и равной

R ^*

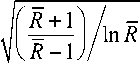
найденной из условия 1 - V ( R *, Z )/ V ( R *, ^ ) = £ ,

где относительная точность £ принимается, как правило, равной 0,02 [16], и ограничиваясь регулярным режимом (в решении (23) учитывается только первое слагаемое ряда), найдено выражение длины начального гидродинамического участка в кольцевом канале:

Z L = f ( R ) Re ,                                         (25)

где                            f ⁽ R ) = ln { НA 1 )/ [e V ⁽ R\ “ ) ] } ;

^ ( A 1 ) = 2 ( CRe - A 12 ) { [ N 0 ( R 1 A 1 ) - N 0 ( R 2 A 1 ) ] J 0 ( R *A 1 ) + [ J 0 ( R 2 A 1 ) - J 0 ( R 1 A 1 ) ] N 0 ( R *A 1 )}/

/{ A 1 ³ [- R 1 J 1 ( R 1 A 1 ) N 0 ( R 2 A 1 ) - R 2 J 0 ( R 1 A 1 ) N 1 ( R 2 A 1 ) + R 2 J 1 ( R 2 A 1 ) N 0 ( R 1 A 1 ) + R 1 J 0 ( R 2 A 1 ) N 1 ( R 1 A 1 ) ] } .

Как следует из (25), длина начального участка пропорциональна числу Re (константа C обратно пропорциональна Re ), что согласуется с оценками [17]. Отметим, что при R → 0 и R → ∞ получаем частные случаи для круглой трубы и плоского канала соответственно (рис. 2). Количественное сравнение полученных результатов проведено с классическими экспериментальными данными [3] (рис. 3). Различие рассчитанных и экспериментальных значений скорости в области, примыкающей ко входному сечению, может быть объяснено тем, что в модели не учитывается расход кинетической энергии потока жидкости на нивелирование неоднородности давления по сечению канала. Тем не менее, это не оказывает существенного влияния на длину гидродинамического участка.

Заключение. Синтезированная модель гидродинамики во входной области кольцевого канала характеризуется качественной и количественной адекватностью и может быть применена для расчета длины начального гидродинамического участка при ламинарном течении вязких несжимаемых жидкостей.