О задаче корректировки регулируемых параметров роторного зернокомбайна

Введение . Высокое качество уборочных работ с применением зернокомбайнов в большой степени зависит от успешного решения задачи управления технологическим процессом, что прежде всего предполагает установление оптимальных значений регулируемых параметров рабочих органов комбайна [1]. Функционирование в меняющихся полевых условиях приводит к тому, что предварительная настройка параметров требует корректировки в соответствии с возможными отклонениями показателей качества уборки от допустимых значений. Среди подобных отклонений повышенные потери свободным зерном, необмолоченным колосом, дробленым зерном, что приводит к существенным финансовым потерям. Наличие подобных отклонений требует оперативной корректировки значений регулируемых параметров комбайна. Решение этой задачи затрудняется сложной системой взаимосвязей между показателями качества уборки и регулируемыми параметрами, а также наличием широкого множества причин, вызывающих данное отклонение, и множеством возможных ответных мер для устранения нарушений, обладающих разной эффективностью.

Задачи технологической настройки комбайнов, как и других сложных многоуровневых систем, решаются применением интеллектуальных систем поддержки принятия решений [2, 3, 4]. Эффективность решения определяется адекватностью математической модели, используемой для вывода решений. В ранее проведенных исследованиях для комбайнов барабанного типа развит целый ряд моделей, в основном регрессионных, в которых установлены некоторые зависимости в отношениях «внешние факторы – регулируемые параметры – показатели качества работы» [5, 6, 7]. Существенным недостатком подобных моделей является то, что в них учитываются только количественные факторы. Невозможность учета качественных характеристик, влияние нечеткости и ограниченный диапазон рабочей области модели привели к тому, что в настоящее время регрессионные модели для таких систем, к которым относятся комбайны, почти не применяются. Для оптимального выбора регулируемых параметров комбайнов барабанного типа успешно применяются нечеткие модели [8, 9]. В то же время для комбайнов роторного типа методология формально-логического описания предметной области отсутствует. На настоящий момент рассмотрены отдельные аспекты технологической настройки роторных зернокомбайнов [10], что определило задачу настоящего исследова- ния как дальнейшего изучения предметной области и разработки методов оптимальной настройки роторного комбайна.

Материалы и методы исследования. В настоящее время зерноуборочные комбайны с аксиально-роторным молотильно-сепариру-ющим устройством (АРМСУ) получают все большее распространение благодаря своей высокой производительности, а в последние годы наблюдается существенный рост спроса на эту технику. В то же время исследования в области оптимальных режимов управления роторными комбайнами только начинаются, необходимые для решения этой задачи зависимости показателей качества работы комбайна от внешних факторов и параметров технологической настройки мало изучены, в отличие от ситуации с классическими комбайнами барабанного типа, для оптимального управления которыми развит целый ряд подходов, используемых в интеллектуальных системах управления [11, 12, 13]. Общими особенностями моделей принятия решений для обоих видов зернокомбайнов является наличие неопределенности и нечеткости в определении значений внешних факторов, сложная система взаимосвязей между регулируемыми параметрами, внешними факторами и показателями качества уборки. Это обуславливает многофакторность задачи принятия решений и наличие нескольких, в том числе гибридных, подходов к её решению. Таким образом, возникает задача разработки подходов к решению задачи оптимального выбора регулируемых параметров роторного комбайна. В настоящей работе рассматривается актуальная для сохранения урожая задача корректировки регулируемых параметров роторного комбайна при обнаружении отклонений показателей качества уборки от допустимых значений.

Решение задачи технологической корректировки настроек рабочих органов роторного комбайна существенно осложняется следующими фактами:

• •    возможностью наличия нескольких отклонений показателей качества работы от допустимых значений;

• •    возможностью существования нескольких причин появления одного нарушения;

• •    существованием различных вариантов устранения одного и того же нарушения;

• •    возможностью появления дополнительного нарушения при устранении первоначально выявленного;

• •    недостатком достоверной информации о возможной причине появления нарушения.

Для анализа предметной области привлекались специалисты в области практической эксплуатации комбайнов, а также непосредственно операторы, имеющие достаточный опыт уборки зерновых культур с использованием роторного комбайна. На основе экспертных суждений и эмпирических данных сформулирован набор внешних признаков возможных нарушений технологического процесса [10]. Обозначим множество внешних признаков нарушения качества работы комбайна Т. На рисунке 1 показано подмножество внешних признаков, связанных с аксиально-роторным молотильно-сепарирующим устройством Т АРМСУ : {Т1, Т2, …, Тn}.

Идентификация предметной области позволила установить основные параметры АРМСУ и их взаимосвязь с внешними признаками нарушений. Для иллюстрации и с целью дальнейшего использования приведем параметры АРМСУ, связанные с рассматриваемым в данной работе отклонением показателей качества уборки – «Потери дробленым зерном» (рисунок 2).

Существенным затруднением в получении оптимального решения является неоднозначность семантических связей «параметр – нарушение». В частности, это проявляется в следующем:

– в среднем одно нарушение обусловлено влиянием пяти параметров как регулируемых, так и конструктивных.

– изменение значения одного из регулируемых параметров может привести к появлению другого нарушения.

Принятие решений по корректировке регулируемых параметров комбайна основано на математической модели реальной системы. Роторный зерноуборочный комбайн относится к сложным многоуровневым техническим системам, функционирующим в непрерывно меняющихся внешних условиях.

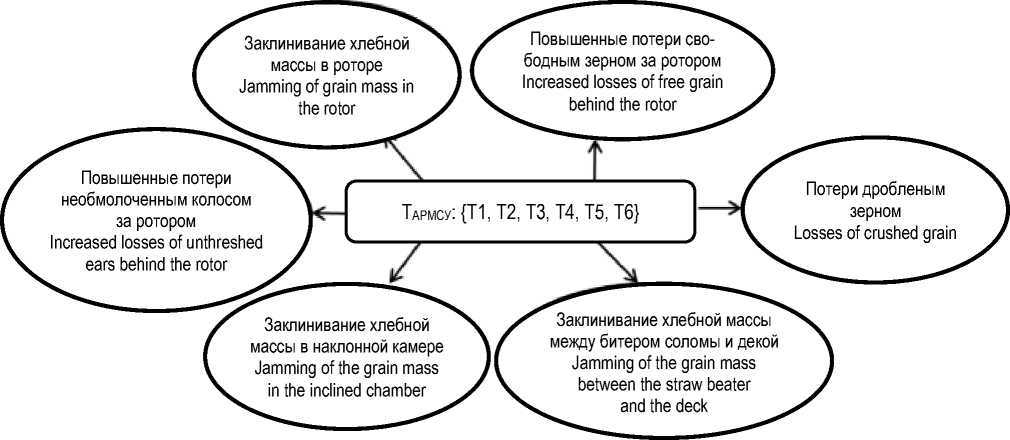
Т АРМСУ : {Т1, Т2, …, Тn}. – подмножество внешних признаков нарушения качества работы комбайна, связанных с аксиально-роторным молотильно-сепарирующим устройством

Рисунок 1 – Возможные нарушения технологического процесса

Т Аrmsu : {T1, T2, …, Tn}. – a subset of external signs of a violation of the quality of the combine harvester, associated with an axial rotary threshing and separating device

Figure 1 – Possible violations of the production processprocess disruptions

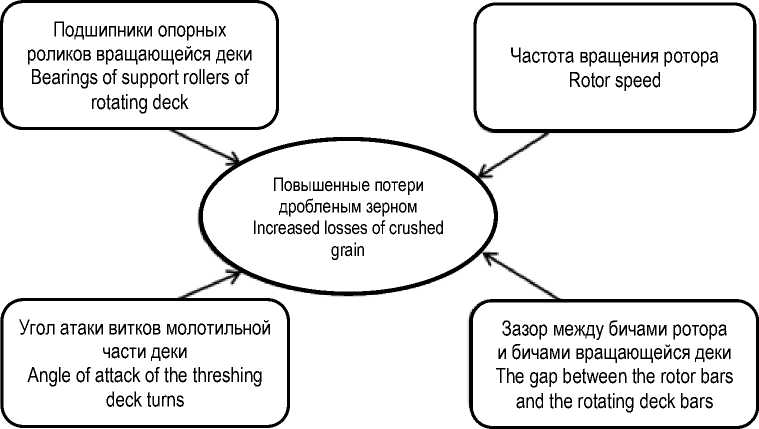
Рисунок 2 – Параметры аксиально-роторного молотильно-сепарирующего устройства, влияющие на наличие нарушения Figure 2 – Parameters of an axial rotary threshing and separating device that influence a violation

Этим обусловлена сложность моделирования процесса принятия решения как по установке начальных значений параметров, так и по их дальнейшей корректировке при появлении признаков нарушения качества уборки. Существует целый ряд подходов к выбору модели принятия решений в подобных задачах, среди которых, например, экспертные системы, основанные на нечеткой логике. Наряду с этим целесообразным является использование теоре- тико-игрового подхода, основанного на выборе стратегии с помощью применения соответствующих критериев для принятия решений в условиях неопределенности. При этом данный подход существенно опирается на эмпирические результаты исследований, теоретические знания и экспертные суждения.

Перейдем к изложению основных положений принятого подхода к моделированию процесса корректировки регулируемых пара- метров комбайна. Рассмотрим функционирующий в полевых условиях комбайн, оператору которого поступил сигнал об отклонении показателя качества уборки от допустимого значения. Применительно к рассматриваемой задаче произошло одно из событий Ti (i=1, 2, … ,6). Отметим, что форма поступления сигнала может быть различной, это как информация от автоматизированной системы контроля для комбайнов, оборудованных такой поддержкой, так и результат визуального контроля оператора. На этом этапе для дальнейшей формализации задачи сформулируем следующие допущения:

– поток поступления сигналов обладает свойством ординарности, то есть появление более чем одного нарушения показателя качества уборки за малый промежуток времени невозможно;

– известны множества регулируемых параметров и технических состояний комбайна, приводящих к каждому из нарушений, а также примерные оценки степени их влияния на появление нарушений.

Множество значений регулируемых параметров и технических состояний, которые могут привести к отклонению показателя уборки Ti, обозначим В = {В/}|”_Множество корректирующих действий, которые могут повлиять на обнаруженное отклонение, обозначим А = {АЛ™Г Множество А представляет собой множество допустимых решений или в терминологии теории игр – множество допустимых стратегий. Каждая из стратегий обладает различной степенью влияния на наблюдаемое нарушение показателя качества уборки. Будем называть меру влияния эффективностью стратегии и оценивать числом, изменяющимся от 0 до 1. Обозначим Ci/ (i = 1,m, j = 1,n.) эффективность стратегии Ai для устранения отклонения В/. Элементы ci/ образуют матрицу С, которую будем называть матрицей показателей эффективности, она является аналогом платежной матрицы в теории «игр с природой». Как и в случае «игр с природой», построение данной матрицы самостоятельная нетривиальная задача, для решения которой необходимо обратиться к накопленным эмпирическим данным, теоретическим соображениям, связанным с конструктивными особенностями комбайна, а также экспертным оценкам по вопросам влияния технического состояния комбайна и значений регу- лируемых параметров на появление различных отклонений в показателях качества уборки.

Теоретико-игровой подход для принятия оптимального решения предполагает использование широкого спектра критериев, каждый из которых имеет свою сферу применения. Причем стратегия, являющаяся оптимальной согласно одному критерию, может быть далека от оптимальности по другому критерию. Выбор того или иного критерия определяется исходными условиями задачи, в том числе широтой экспертной базы знаний. Остановимся подробно на критериях, применение которых целесообразно для решения поставленной задачи корректировки.

При отсутствии базы знаний об эмпирических частотах причин, вызывающих отклонения показателей качества уборочных работ, можно принять гипотезу о равновероятном распределении, опираясь на принцип недостаточного обоснования [14]. В этом случае используют критерий Лапласа, который в качестве оптимальной выбирает стратегию с максимальной средней эффективностью:

maxL(i) = max l Yj^c^ . (1)

Эта ситуация может быть характерна для оператора, не имеющего опыта и возможности опереться на базу экспертных знаний. В современных условиях часто имеется база ранжированных по частоте возникновения причин нарушения, она позволяет получить оценочные вероятности. Принимая их в качестве априорных вероятностей р / ( j = 1,n ) наличия причин {В / } , целесообразно использовать аналогично построенный критерий максимального математического ожидания (МО):

maxM(i) = max^j^^C i/ P / . ⁽²⁾

При высокой значимости риска принятия неверного решения можно воспользоваться критерием Сэвиджа [14], также называемым критерием минимального риска. Для его применения строят матрицу R рисков, элементы которой ц (i = 1,m, j = 1,n.) отражают риск неэффективного применения стратегии Ai для устранения нарушения В/. Если бы причина нарушения В/ была бы известна, то применили бы стратегию Ai с максимальным показателем эффективности, что соответствует максимальному элементу βj в столбце с номером j. Эле- менты матрицы рисков r вычисляют по фор- муле rij = Pj - cij.                  (3)

Оптимальной согласно критерию Сэвиджа является стратегия с минимальным риском в наихудших условиях:

minS(i) = minmaxr_i j .

i                    i       j      J

Выбор критериев для решения задачи щенной схемой, представленной на рисунке 3. В случае отсутствия эмпирической информации о частоте причин, приводящих к появлению отклонения, используют критерий Лапласа. Наличие такой информации определяет выбор стратегии, соответствующей критерию математического ожидания, а в ситуации, в которой при отсутствии информации велик риск неверного решения, применяют критерий Сэвиджа.

осуществляется оператором в зависимости от исходной ситуации и проиллюстрирован обоб-

УСЛОВИЯ ПРИНЯТИЯ РЕШЕНИЯ DECISION-MAKING CONDITIONS

КРИТЕРИИ CRITERIA

СТРАТЕГИИ STRATEGII

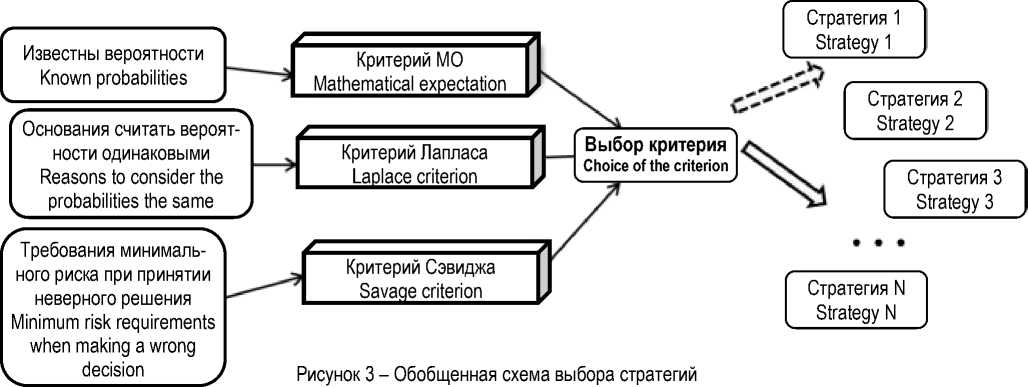
Figure 3 – Generalized scheme for choosing strategies

Обратимся к задаче корректировки регулируемых параметров роторного комбайна и рассмотрим на примере конкретного нарушения показателя качества уборки применение приведенных выше критериев выбора оптимальной стратегии для устранения обнаруженного отклонения.

Результаты исследования и их обсуждение. Одним из распространенных при уборке зерновых культур внешних признаков отклонения показателей качества является следующий «Потери дробленым зерном» (см. рисунок 1). Проведенный анализ отношений «причины – возможные стратегии устранения нарушения», основанный на эмпирических данных и теоретических соображениях, позволил выявить возможные причины данного нарушения и ответные меры реагирования, направленные на его устранение (рисунок 4). Среди причин нарушения указана изношенность подшипников, возможным действием в этом случае является их замена, что не относится к регулиров- кам параметров, а относится к действиям конструктивно-технологического характера и рассматривается также как стратегия действий.

На основе эмпирических данных и экспертных суждений получена матрица значений показателей эффективности {Q j } (таблица 1).

Рассмотрим особенности применения критериев для выбора оптимальной стратегии. Начнем с ситуации, когда отсутствует информация об оценках вероятностей конкретных причин, вызвавших данное отклонение. Тогда принимаем допущение, что вероятности причин одинаковы, и выбираем в качестве оптимальной согласно критерию Лапласа (1) стратегию, которая имеет максимальную среднюю эффективность. Рассчитанные значения величин критерия Лапласа приведены в таблице 1 в столбце L ( i ). Оптимальной по критерию Лапласа является стратегия А 3 – уменьшение угла атаки витков молотильной части деки путем их смещения на 1/3 регулировочного паза.

Причины нарушения

• В 1 .    Изношены подшипники опорных роликов вращающей деки или имеются выработки на роликах.

• В 2 .    Неравномерный зазор между бичами ротора и бичами вращающейся деки.

• В 3 .    Большой угол атаки витков молотильной части деки.

• В 4 .    Высокая частота вращения ротора (ЧВР)

  
  
  

Reasons for violation

• В 1 .    The bearings of the support rollers of the rotating deck are worn out or there are grooves on the rollers.

• В 2 .    Uneven gap between the rotor bars and the rotating deck bars.

• В 3 .    Large angle of attack of the the threshing deck turns.

• В 4 .    High rotor speed (HRS)

Возможные стратегии действий

• А 1 . Привести в исправное состояние (заменить) подшипники опорных роликов.

А 2 . Отрегулировать (выставить одинаковыми) зазор между бичами ротора и бичами вращающейся деки.

А 3 . Уменьшить угол атаки витков молотильной части деки путем их смещения на 1/3 регулировочного паза.

А 4 . Уменьшить ЧВР на 50 мин^-1.

А 5 . Уменьшить ЧВР на 70 мин^-1.

Possible action strategies

A1. Repair (replace) the support roller bearings.

A2. Adjust (set equal) the gap between the rotor bars and the rotating deck bars.

A3. Reduce the angle of attack of the threshing deck turns by shifting them by 1/3 of the adjustment groove.

A4. Reduce HRS by 50 min- ^-1 .

A5. Reduce HRS by 70 min- ^-1 .

Рисунок 4 – Схема отношений «причины – возможные стратегии устранения»

Figure 4 – Scheme of the relationship «causes – possible elimination strategies»

Таблица 1 – Матрица значений показателей эффективности и величин критериев Table 1 – Matrix of values of performance indicators and values of criteria

А i	B j				L ( i )	M( i )
	B 1 0,45	B 2 0,3	B 3 0,1	B 4 0,15
A 1	0,98	0,2	0,1	0,05	0,3325	0,5185
A 2	0,3	0,95	0,3	0,1	0,4125	0,465
A 3	0,15	0,35	0,98	0,5	0,495	0,3455
A 4	0,3	0,05	0,6	0,9	0,4625	0,345
A 5	0,35	0,05	0,65	0,9	0,4875	0,3725
β j	0,98	0,95	0,98	0,9
Оптимальная стратегия Optimal strategy					A 3	A 1

Очевидно, что при наличии данных наблюдений за процессом эксплуатации комбайнов можно получить значения относительных частот, приводящих к отклонению рассматриваемого показателя качества уборки. Принимая их в качестве вероятностей, можем использовать критерий максимального математического ожидания (2). Эмпирические оценки вероятностей причин B j приведены в таблице 1 в клетках B j , а вычисленные значения критериев – в крайней правой колонке. Согласно этому критерию оптимальной является стратегия А 1 – привести в исправное состояние или заменить подшипники опорных роликов вращающейся деки.

Перейдем к анализу использования критерия Сэвиджа. В этом случае оптимальная стратегия выбирается на основе анализа рисков r принятия неэффективного решения. Найдем элементы матрицы рисков по формуле (3), отметим, что значения максимальных элементов по столбцам указаны в нижней строке таблицы 1 в соответствующих колонках. Рассчитанные значения элементов матрицы рисков и значений величины критерия Сэвиджа представлены в таблице 2.

Из таблицы 2 видим, что согласно критерию Сэвиджа оптимальной стратегией будет А 2 – отрегулировать зазор между бичами ротора и бичами вращающейся деки.

Наряду с приведенными критериями для задач принятия решений в условиях неопределенности используют и другие критерии, такие как критерии Вальда, Гурвица и их модификации [15, 16]. Наряду с применением критериев могут быть рассмотрены и иные подходы к учету неопределенности [17].

Таблица 2 – Матрица рисков и величины критерия Сэвиджа Table 2 – Risk matrix and Savage criterion values

А i	B j				S( i )
	B 1	B 2	B 3	B 4.
A 1	0	0,75	0,88	0,85	0,88
A 2	0,68	0	0,68	0,8	0,8
A 3	0,83	0,6	0	0,4	0,83
A 4	0,69	0,9	0,38	0	0,9
A 5	0,63	0,9	0,33	0	0,9
Оптимальная стратегия Optimal strategy					A 2

Выводы. На современном этапе аграрный сектор предъявляет все возрастающие требования к сельскохозяйственной технике, в том числе зерноуборочным комбайнам. Одним из важнейших требований является сбережение урожая и его высокое качество, что предполагает совершенствование конструкций уборочной техники, а также внедрение интеллектуальных автоматизированных систем управления, в которых используются процедуры предварительной технологической настройки и процедуры обратной связи. Последние предназначены для обнаружения отклонений показателей качества от требуемых значений и связаны с блоком корректировок настроек, в котором осуществляется выбор оптимального реагирования для устранения отклонений. В настоящей работе предложен подход к задаче выбора оптимальной стратегии реагирования на обнаруженное отклонение показателей качества работы применительно к роторным зерноуборочным комбайнам. Данный подход основан на использовании различных критериев оптимальности, таких как максимальная ожидаемая эффективность или минимальный риск неэффективного решения. Применение данного подхода, который имеет широкое распространение в задачах принятия решений в условиях неопределенности, предполагает наличие достаточной базы экспертных знаний и эмпирических результатов, чтобы сформулировать стратегии действий и дать оценку их эффективности в различных ситуациях. Предложенный метод не требует существенных вычислительных затрат, а с другой стороны, позволит накапливать информацию об эффективности стратегий, тем самым расширяя базу экспертных знаний. Таким образом, предложенный подход может найти применение в блоке корректировки интеллектуальной системы, основанной на нечетком моделировании вывода решения, в частности для определения весомости правил нечеткой продукции, а также в гибридных системах, использующих нейронные сети и машинное обучение.